机器学习(Andrew Ng)学习笔记(第13~15章)
支持向量机
SVM的代价函数
首先回顾不带正则化的逻辑回归的代价函数:
令\(z=\theta^Tx^{(i)}\),则\(-log(Sigmoid(\theta^Tx^{(i)})),-log(1-Sigmoid(\theta^Tx^{(i)}))\)的图像如下所示:

令\(cost_1(\theta^Tx^{(i)})=-log(Sigmoid(\theta^Tx^{(i)}))\),\(cost_0(\theta^Tx^{(i)})=-log(1-Sigmoid(\theta^Tx^{(i)}))\),分别代表\(y^{(i)}=1,0\)时的损失。
则优化目标为:
可见\(y^{(i)}=1\)时,这个优化目标倾向于使得\(\theta^Tx^{(i)}\to +\infty\);\(y^{(i)}=0\)时,这个优化目标倾向于使得\(\theta^Tx^{(i)}\to -\infty\),即让决策边界尽量远离每个数据点
再对上式补上正则化:
SVM的决策函数,就是用新的cost函数(这里采用hinge损失)代替原有函数:
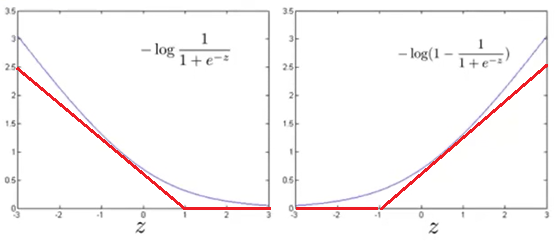
在新的优化目标下,\(y^{(i)}=1\)时,这个优化目标倾向于使得\(\theta^Tx^{(i)}\geq 1\);\(y^{(i)}=0\)时,这个优化目标倾向于使得\(\theta^Tx^{(i)} \leq -1\)
其中,\(m\)是常数,可以省去:
用\(C=\frac 1 \lambda\)代入,可以改写为
优化目标还可以改写为:
(实际上这个约束条件并不是硬性约束,即允许少量\(x^{(i)}\)不满足这一约束条件,用惩罚常数\(C\)来控制不满足条件的\(x^{(i)}\))
同时,SVM的假设函数也发生了变化:
可见,\(\theta^Tx=0\)就是SVM的决策边界
直观上对大间隔的理解

SVM又被称为大间隔分类器(large margin classifier),即SVM倾向于找出距离所有正、负样本的距离更大的决策边界,如上图,在五条可选的决策边界中,SVM倾向于选择加粗的那一条,因为这个边界距离所有正、负样本更远
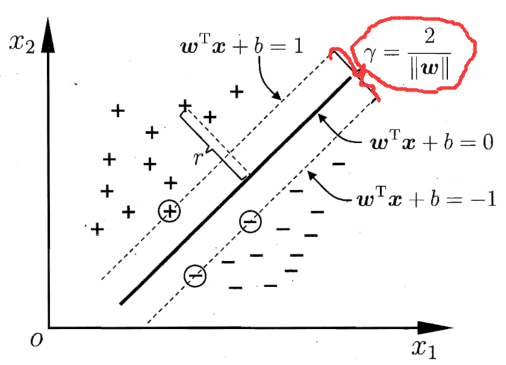
距离决策边界最近的正样本到边界的距离+距离决策边界最近的负样本到边界的距离=间隔(margin),如上图红色所示
惩罚常数C越大,SVM越倾向于找到使得训练集分类正确率更高的样本,也越倾向于过拟合。
大间隔分类器的数学原理
回顾SVM的优化目标:
为了便于理解,下面考虑的是\(\theta_0=0\)的情况。
直白地讲,上面的优化目标就是:在保证绝大多数训练样本被正确分类的前提下,使得参数向量\(\theta\)的范数\(\|\theta\|\)尽量小,而约束条件也可改写为:
(\(\alpha\cdot \beta\)为两个向量的点积)
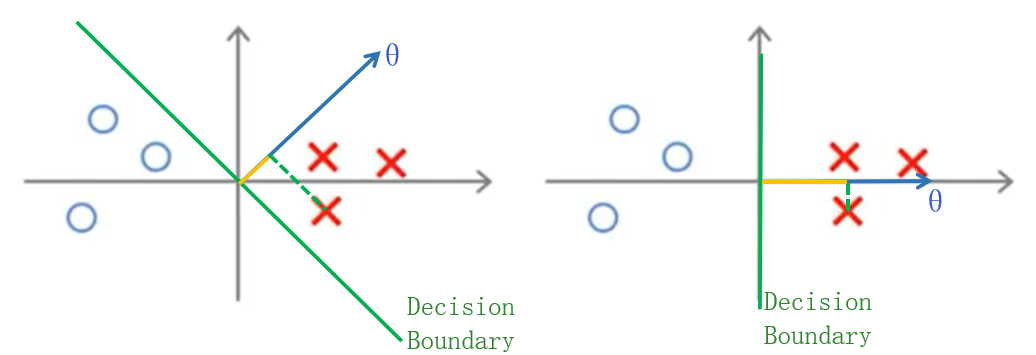
如上图,左右分别是两种不同的可选的决策边界(\(\theta^Tx=0\)),左右的\(\|θ\|\)相同,可见同一个样本在两个\(\theta\)上的投影长度(图中黄色)不同,左图比右图的小,换言之,为了保证尽可能多的点满足上文的约束条件,以左图\(\theta\)的方向,需要更大的\(\|\theta\|\),优化目标决定倾向于选择右图的\(\theta\)方向,显然右图的间隔比左图大很多。
这就是SVM倾向选择大间隔决策边界的数学原理。\(\theta_0\neq 0\)时的情况也与此类似,只不过决策边界不再过原点。
核函数
之前提到的SVM,其决策边界是线性方程\(\theta^Tx=0\),只能解决线性可分的问题。为了解决线性不可分问题,可以考虑构造更高阶的特征,但是类似于神经网络面临的问题一样,实际问题中,输入的特征数目非常多,如果构造更高阶的特征,最终构造出的特征数目太多,无法有效训练。
这里引入了核函数(kernel function)的概念。
设一共有\(m\)组训练样本。我们用函数\(\mathrm{sim}(x_1,x_2)\)表示两个向量\(x_1,x_2\)之间的相似程度,二者越相似,函数值越趋于1,反之越趋于0。
然后将原始的第\(i\)个数据\(x^{(i)}\)的\(n\)个特征投射到新的\(m\)个特征:
若训练样本数\(m\)大于特征数\(n\),这样便可以大幅扩充特征数目了
下面举例说明核函数的作用,设\(m=3,\theta=(-0.5,1,1,0)^T\)

将输入数据的特征用核函数的方法投射为\((f_1,f_2,f_3)\),可见输入数据距离训练样本1和2越近,\(\theta^Tf\)越大,决策边界表现为围绕样本点1和样本点2的一个封闭曲线,这样就实现了非线性决策边界
最常用的核函数是高斯核(Gaussian kernel):

其中,参数\(\sigma^2\)是方差,\(\sigma^2\)越大,\(x_1,x_2\)距离增大时,核函数的函数值减小得越缓慢。如上图。
另外还有线性核(linear kernel),其实就是不加核函数;多项式核,等等。
SVM实现多元分类
SVM实现多元分类可以类比逻辑回归的多元分类,即,若有K个分类,则设计K个分类器,第i个分类器判断输入数据分类是否为i
SVM vs. 逻辑回归 vs. 神经网络
当特征数n<样本数m,且m大小适中时,可以采用带核函数的SVM
当特征数n远大于样本数m时,应当采用逻辑回归或不加核函数的SVM
当特征数n远小于样本数m时,应当构造或添加更多的特征,使用逻辑回归或不加核函数的SVM
对于以上三种情况,神经网络均能很好地适用,但神经网络的训练明显远远慢于SVM和逻辑回归
K-Means聚类
K-Means聚类的任务是,给定分类数K,将所有数据点划归为K类,并确定每一类的聚类中心
优化目标
根据以上叙述,K-Means的优化目标可表示为:
其中\(idx(i)\)为第i个数据点所属归类,\(\mu_i\)为第i个聚类的中心点
算法流程
-
Repeat{
-
-
\[\arg\ \min_{idx(1),\cdots,idx(m)}J(idx(1),\cdots,idx(m),\mu_1,\cdots,\mu_K)$$,即:为每个数据点寻找最近的聚类中心来确定新的归类 \]
-
-
}while(数据点的归类在本次循环中发生变化)
随机初始化
初始化聚类中心非常关键,初始化不当是无法得到较好的聚类结果的。
通常是随机从m个数据点中抽取K个点作为聚类中心
另外,聚类结果具有一定的随机性,因此若K较小时,需要重复多做几次聚类,取最好的一次聚类结果。但K接近于数据数目m时,一次聚类就够了。
选取聚类数目
当聚类目的非常明确,已知需要聚成几类,就聚成几类
当聚类目的不明确时,可以从小到大尝试K的取值,并绘制出代价函数J关于K的折线图,选取折线图"肘部"的K作为聚类数目。
主成分分析PCA
动机
1、数据压缩
PCA可以用于数据压缩:
-
1、可以减少数据在硬盘中的存储空间;
-
2、可以在训练前减少数据的特征数目,从而减少模型的参数数量,提高训练速度
2、数据可视化
PCA可以将高维数据降维到二维或三维,从而能从数据分布图中直观看出数据之间的关系
算法流程
假设原始数据点(\(X=(x^{(1)},\cdots,x^{(m)})^T\))均为n维特征,任务是找到K维子空间及该子空间的K个基,将它们投影到该子空间,并得到它们用这K个基表示的坐标,从而降到K维特征。
注意:在这个K维子空间上,所有数据点的投影点分布的差异最大,最能体现出这些点之间的差异性。
(1)求投影到的K维子空间的基
设\(\Sigma\)为所有数据点构成的协方差矩阵。
首先,找到这些数据点投影到的K维子空间的K个基,可以选取\(\Sigma\)特征值最大的前K个特征向量,即svd()返回的特征向量里的前K个:\(u^{(1)},\cdots,u^{(K)}\)
(2)对原始数据降维
svd()函数返回的特征向量均为单位向量,对于某组数据(列向量\(x^{(i)}\)),对其降维就是将其投影到\(C(u^{(1)},\cdots,u^{(K)})\)子空间,即降维后的向量为:
令\(U_{reduced}=(u^{(1)},\cdots,u^{(K)})\),则
(3)还原数据
还原数据就是已知原始数据投影到新的K维子空间上的坐标,用这些坐标与子空间的K个基线性组合。
给出降维到K维后的若干组数据构成的矩阵Z,Z中每一行代表一组降维后的数据,以及协方差矩阵的特征向量(列向量)构成的矩阵U,恢复出原始数据X_rec
对于每组降维后的数据\(z^{(i)}\),只需将前K个特征向量按\(z^{(i)}\)线性组合即可恢复数据
算法演示
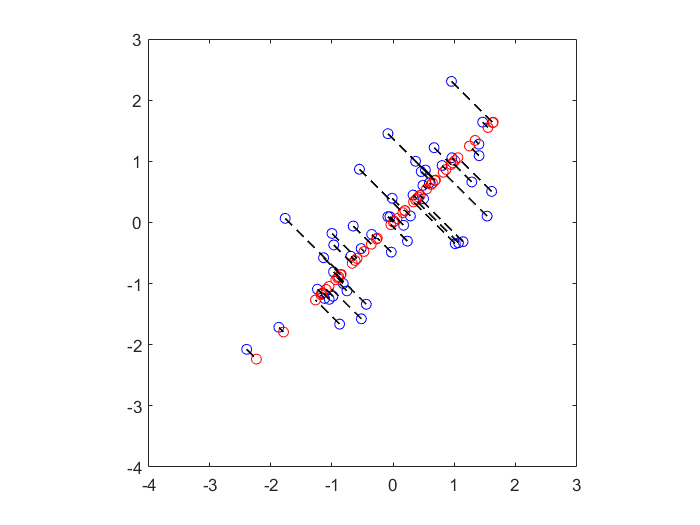
以下将二维特征的数据降维到一维特征
1、找到一维子空间及其基(图中较长的黑线)
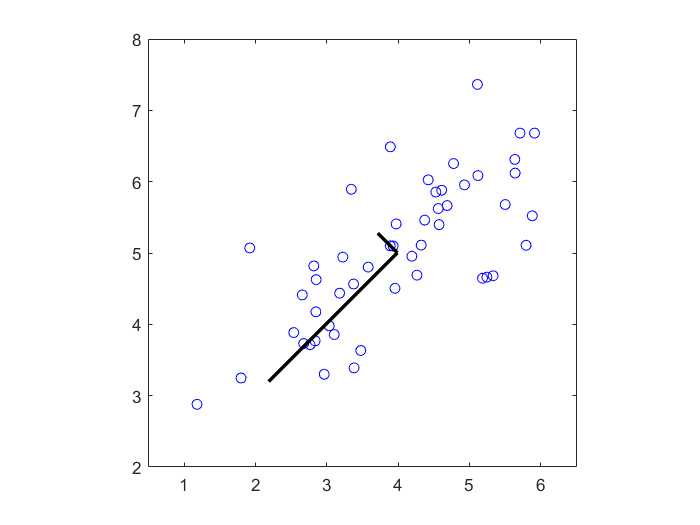
2、将原始数据点(蓝色)投影到该一维子空间,重构出的数据点为红色点
选取主成分数目的原则
用\(\frac 1 m \sum_{i=1}^m\|x^{(i)}-x_{approx}^{(i)}\|^2\)表示重构数据与原始数据之间的差异,\(\frac 1 m \sum_{i=1}^m\|x^{(i)}\|^2\)表示原始数据的大小,则重构误差可以表示为:
若
则表明99%的原始数据都被保留了下来
在选取主成分数目时,首先确定最少要保留原始数据的比例为多少,然后从小到大尝试主成分数目K的取值,选择最小的K,满足这个比例。
应用PCA的建议
PCA的不当使用
-
a.使用PCA防止过拟合
-
b.在逻辑回归等分类算法使用之前用PCA对数据降维,这样有可能丢失一些与标签相关的特征
应用PCA的建议
在使用PCA前,最好先尝试不用PCA,在确定了PCA会给整个算法带来帮助后再加入PCA

