球面镜成像原理，焦距推导

半球体的焦点公式推导

一个半球体半径为R水平放置(与水平面接触的是半球面的最大的面)，用圆形的光线垂直向半球体发射，在半球体的外表面形成一个圆形，假设此时该圆形的半径为r，那么，
问题1：所有反射光线的反向延长线会相交于一点吗？如果会，为什么？
问题2：改变圆形的光线的投射高度，即改变了投射到半球面圆形的半径，此时反射光线的反向延长线相交于一点，那么问题1和问题2的两个点一样吗？如何用立体图表现？

 

=====================================================================
题主的问题是单纯的几何光学。
从题主的问题描述中「问题2：改变圆形的光线的投射高度，即改变了投射到半球面圆形的半径」这句话看，题主假设的是一个点光源吧？也就是下面这种场景


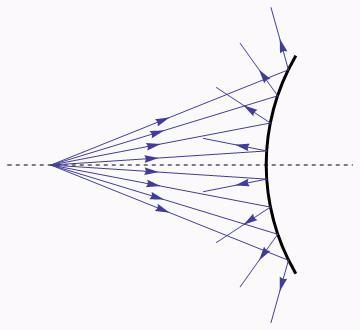
那么，很遗憾地告诉你，这些反射光线反向延长后并不汇聚到一个点上，这种现象叫做球差（球面像差）。
如果题主懂解析几何的话，不妨自己建立坐标系算一算。
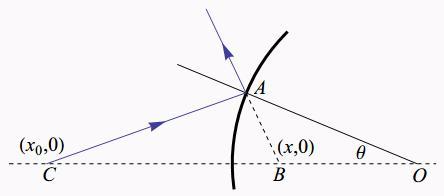我这里帮你算了一个（假设球心在原点），B 点的坐标是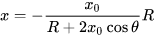
x=-\frac{x_0}{R+2x_0\cos\theta}R

我想，这个式子能解答题主的两个问题了。
回答1：不会，上面那个式子里含有角度，说明反射光线的反向延长线的交点是随着角度不同而变化的。
回答2：不是，上面那个式子里含有光源的位置，说明不同位置的光源反射光线的反向延长线的位置也是不同的。

给一些直观的结果吧。
假设 x0 = -3R（也就是距离半球面顶部 2R），那么B点的坐标随角度的变化是这样的：


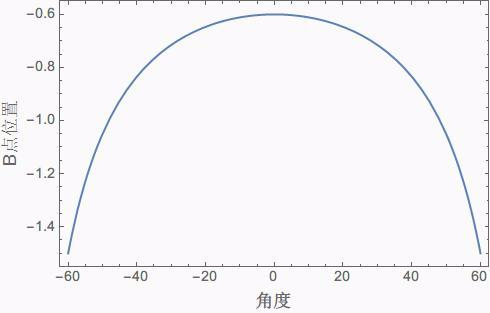
这里 B 点的位置随着角度不同而不同的现象就叫做「球差」了。

那么，为什么在中学课本中说到凸面镜的时候说「凸面镜对实物成一个正立缩小的虚像」呢？如果光线的反向延长线不交于一点，那怎么成像呢？
答案就是：对于近轴光线，「反向延长线交于一点」这个结论是对的

什么是近轴光线？简单说，就是离光轴特别近的光线。对应到上面这个例子来，就是角度 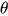\theta 特别小的光线。
直观来说，你看上面这个曲线，在角度接近0的部分是不是相对比较平坦？说明在角度很小的时候，角度的变化对于 B 点位置的变化是影响不大的。这一点其实很容易证明，把 B 点坐标的表达式在 0 点进行级数展开：
x=-\frac{x_0}{R+2x_0}R-\frac{x_0^2}{(R+2x_0)^2}\theta^2R+O[\theta^4]
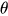当\theta很小的时候，上面第二项开始就都可以忽略了，也就是 B 点位置与角度无关。
中学课本里说的所有的结论和公式，全都是在近轴光学范畴里成立的，包括各种透镜成像公式/规律，球面镜成像公式/规律。

再多说一句，如果将 C 点到球面顶点的距离作为物距离 u，将 B 点到球面顶点的距离作为像距 v，那么，在近轴条件下可以得到
u=-(R+x_0)
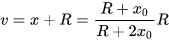
v=x+R=\frac{R+x_0}{R+2x_0}R
所以简单代换一下就可以得到：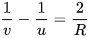
\frac{1}{v}-\frac{1}{u}=\frac{2}{R}
看，凸球面镜的成像公式就这么来了，而且可以看出，R/2 就是球面镜的焦距。

其实，从 B 点位置的表达式也可以直接推出球面镜的焦距，令 x0 趋向负无穷：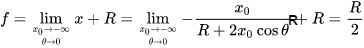
f=\lim_{{x_0\rightarrow-\infty}\atop{\theta\rightarrow0}}{x+R}=\lim_{{x_0\rightarrow-\infty}\atop{\theta\rightarrow0}}{-\frac{x_0}{R+2x_0\cos\theta}+R}=\frac{R}{2}

再再多说一句，近轴光学里的光线行为是线性的，这大大简化了光线的计算。光线的传播、折射、反射都可以用矩阵来描述，上面@Zhang Tianyi兄弟的答案说的就是这么回事。最早由高斯（是的就是那个大名鼎鼎的高斯）系统地总结归纳了近轴光学的性质，并用纯粹的代数学来计算光学系统的所有行为，建立了近轴光学的理论基础，所以近轴光学也叫高斯光学。完毕。

 

 

 

 

 

 

发布于 2014-11-10
作者：章佳杰
链接：https://www.zhihu.com/question/26552292/answer/33192992
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

来自为知笔记(Wiz)



posted @ 2018-08-24 15:28  Jerry_Jin  阅读(15256)  评论(0)  编辑  收藏  举报