隐马尔可夫模型维特比算法详解
隐马尔可夫模型维特比算法详解
关于隐马尔可夫模型的维特比解码算法网上已有一大批文章介绍,故本文不再介绍。
本文主要是在读《自然语言处理简明教程》和看HanLP 中文人名识别源码过程中,对该算法的一次梳理,以防忘记。
隐马模型有三个问题,其中二个是:
- 给定HMM模型 \(\lambda\) 和一个观察序列O,确定观察序列O出现的可能性\(P(O|\lambda)\)
- 给定HMM模型\(\lambda\) 和一个观察序列O,确定产生O的最可能的隐藏序列Q
第一个问题用向前算法解决,可参考:隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率
第二个问题用维特比算法解决,可参考:隐马尔科夫模型HMM(四)维特比算法解码隐藏状态序列
下面记录下我对这两个算法的理解。
向前算法
将\(P(O|\lambda)\)简写成\(P(O)\),观察状态是由隐藏状态生成的,因此:任何一个可能的隐藏状态\(Q=(q_1,q_2,...q_N)\)以一定的概率生成观察状态O。故:
根据贝叶斯公式:\(P(O,Q)=P(O|Q)*P(Q)\)
所以:\(P(O)=\Sigma_{Q}{P(O|Q)*P(Q)}\)
对于一个长度为T的观察序列,书中第518页指出:一共有\(N^T\)种可能的隐藏状态。将这\(N^T\)个隐藏状态生成序列O的概率求和,就得到了\(P(O)\),但这种方法的时间复杂度是指数级的:\(O(N^T)\)
根据隐马尔可夫模型的独立输出假设:
根据概率论中的链式法则:
再根据隐马尔可夫模型的一阶马尔可夫链假设:
简化一下,就是:
因此:对于一个特定的隐藏状态\(Q^*\)
这里:\(p(q_i|q_{i-1})\)就是从隐藏状态\(q_{i-1}\)转移到隐藏状态\(q_i\)的转移概率;
\(p(o_i|q_i)\)就是隐藏状态\(q_i\)生成观察状态\(o_i\) 的 发射概率。
正是根据转移概率和发射概率 定义:\(\alpha_t(j)\),从而采用动态规划的方法来求解:\(P(O|\lambda)\)
动态规划方法
定义:\(\alpha_t(j)=P(o_1,o_2,...o_t, q_t=j|\lambda)\)生成了\(t\)个观察后,在时刻\(t\)隐藏状态\(q\)取值为\(j\)的概率,用公式表示成:
这相当于动态规则的状态方程。上面公式中有个\(\Sigma\),在书中第586页的图9.8 解释了 求和符号的意义:
- 在\(t-1\)时刻的每一个隐藏状态\(q(i)\)的取值概率\(\alpha_{t-1}(i)\) 乘以 从状态i 转移 到 状态j 的概率 再乘以 \(t\) 时刻状态j 生成 观察状态\(o_t\)的概率
- 对上行中所说的: 每一个求和
对于动态规则,有两个性质:最优子结构和重叠子问题。
\(\alpha_{t-1}(j)\)是\(\alpha_{t}(j)\)的子结构,\(\alpha_{t-2}(j)\)是\(\alpha_{t-1}(j)\)的子结构,因为问题的规模变小了。
重叠子问题:要求解\(\alpha_{t}(j)\),需要求解\(\alpha_{t-1}(j)\),要求解 \(\alpha_{t-1}(j)\)需要求解\(\alpha_{t-2}(j)\)……
那么\(\alpha_{t-2}(j)\)就是求解 \(\alpha_{t}(j)\) 和 \(\alpha_{t-1}(j)\) 的一个重叠子问题。
如果在自底向上求解过程中,把这些子问题记录下来:将\(\alpha_{1}(j)\)、\(\alpha_{2}(j)\)……都保存起来,当使用到它们时,直接“查表”,那么计算起来会快很多。关于这种思想,可参考:动态规划之Fib数列类问题应用
书中有向前算法的详细示例。这里不再介绍。
维特比算法
这里的维特比算法和上面的向前算法其实是非常相似的。向前算法是对 \(t-1\)时刻中的每个[隐藏状态的概率 乘 转移概率 乘 发射概率] 求和;
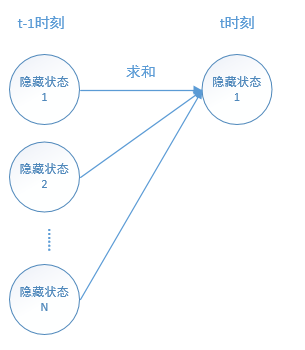
而维特比算法则是:根据 向前算法 \(t-1\)时的求和得到 \(t\)时刻的某个隐藏状态概率,而 \(t\) 时刻 一共有N个隐藏状态概率,算法选出这 N个隐藏状态中 概率值 最大的那个 隐藏状态。
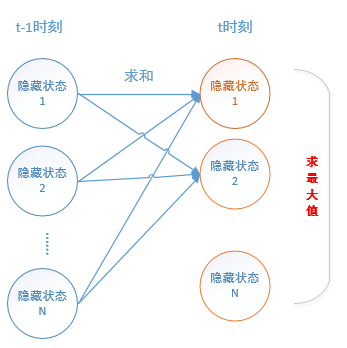
而求解\(t\)时刻N个隐藏状态概率的最大值有两种方法:一种方法是暴力法,第587页已经讲了。另一种是动态规划方法,下面记录一下动态规划方法的求解思路。
动态规划
\(v_t(j)\)表示:在 \(t-1\)时刻的 每个隐藏状态(共有N个) 乘以 转移概率 乘以 发射概率 得到一个结果,取这N个结果的最大值 (这也是最终求得的结果是最优的原因---不是贪心思路)作为 t 时刻 \(j\) 状态的概率。由于一共有N个隐藏状态,在\(t\)时刻,需要求解:\(v_t(1)\)、\(v_t(2)\)……\(v_t(N)\)
写出动态规划的状态方程如下:
\(t\)代表时间,范围为1,2...T,\(a_{ij}\)代表隐藏状态转移矩阵的概率,即从隐藏状态\(q_i\)转移到\(q_j\)的概率。\(b_j(o_t)\)代表发射概率,即\(t\)时刻的隐藏状态\(q_j\)生成观察状态\(o_t\)的概率。 具体详细的示例解释参考书上第587页开始的讲解。
下面用代码验证一下理论的正确性:
参考:通用维特比算法实现并针对《自然语言处理简明教程》第9章隐马尔可夫模型介绍,验证了在观察状态 3 1 3 时最佳隐藏状态为 H H H。具体验证代码如下,并加了一些注释。
import static org.hapjin.hanlp.Viterbi.Activity.one;
import static org.hapjin.hanlp.Viterbi.Activity.two;
import static org.hapjin.hanlp.Viterbi.Activity.three;
import static org.hapjin.hanlp.Viterbi.Weather.hot;
import static org.hapjin.hanlp.Viterbi.Weather.cold;
public class Viterbi {
static enum Weather
{
cold,
hot,
}
static enum Activity
{
one,
two,
three,
}
static int[] states = new int[]{cold.ordinal(), hot.ordinal()};
// static int[] observations = new int[]{one.ordinal(), two.ordinal(),three.ordinal()};
static int[] observations = new int[]{three.ordinal(), one.ordinal(),three.ordinal()};
static double[] start_probability = new double[]{0.2, 0.8};
static double[][] transititon_probability = new double[][]{
{0.6, 0.4},//cold
{0.3, 0.7},//hot
};
static double[][] emission_probability = new double[][]{
{0.5, 0.4, 0.1},//cold
{0.2, 0.4, 0.4},//hot
};
public static void main(String[] args)
{
int[] result = Viterbi.compute(observations, states, start_probability, transititon_probability, emission_probability);
for (int r : result)
{
System.out.print(Weather.values()[r] + " ");
}
System.out.println();
}
public static int[] compute(int[] obs, int[] states, double[] start_p, double[][] trans_p, double[][] emit_p)
{
//动态规划中保存 当前最优结果, 供后续计算 直接 "查表"
double[][] V = new double[obs.length][states.length];//v_t(j)
//保存最优路径
int[][] path = new int[states.length][obs.length];//[state][t]
for (int y : states)
{
V[0][y] = start_p[y] * emit_p[y][obs[0]];//t=0 (t=0代表起始隐藏状态)
path[y][0] = y;
}
//时间复杂度: (T-1)*N*N=O(T*N^2)
// T-1
for (int t = 1; t < obs.length; ++t)
{
int[][] newpath = new int[states.length][obs.length];//应该是可以优化一下的.
//N 个隐藏状态 即:{cold, hot}, N=2
for (int y : states)
{
double prob = -1;
int state;
//N
for (int y0 : states)
{
// v_{t-1}(i)*a_{ij}*b_j(o_t)
double nprob = V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]];
//find max
if (nprob > prob)
{
prob = nprob;
state = y0;
// 记录t时刻 隐藏状态为y 时的最大概率
V[t][y] = prob;//t是第一个for循环参数, y 是第二个for循环参数
// 记录路径
System.arraycopy(path[state], 0, newpath[y], 0, t);//
newpath[y][t] = y;//将t时刻 最佳隐藏状态 y 保存
}
}
}
path = newpath;
}//end outer for
double prob = -1;
int state = 0;
//找出最后那个时刻的 V_T(j) j=1,2...N 的最大值 对应的隐藏状态y
for (int y : states)
{
if (V[obs.length - 1][y] > prob)
{
prob = V[obs.length - 1][y];
state = y;
}
}
return path[state];//根据上面 max{V_T(j)} 求得的y "回溯" 得到 最优路径
}
}
《自然语言处理简明教程》里面详细介绍了HMM三个问题的求解过程,通俗易懂。
另外想学习一下概率图模型,不知道有没有好的书籍推荐?
参考链接:HanLP中人名识别分析
原文链接:http://www.cnblogs.com/hapjin/p/9033471.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号