【初等概率论】 05 - 极限定理和正态分布
1. 极限定理
至现在为止,概率论仿佛还算简单,只是把一些直观的东西用数学语言表达出来而已。当有了实变和泛函的基础后,你会发现概率论只是分析学的一个普通特例,故更丰富的内容还需我们提升之后再去欣赏。概率论中很多极限问题,一度成为其核心课题,它们不仅发掘了更多有趣的结论,更是解释了很多深层的随机现象。极限定理需要很多高级的分析学工具,故这里仅做结论性的介绍,一是体会高级概率论的无穷奥妙,二是为数理统计准备必要的结论。
1.1 大数定律
我们还是要回答最初的问题:概率究竟什么?我们建立的概率系统与直觉上的概率是否兼容?起初我们就把事件和固定的数值挂钩,就假定了随机事件有一个不变的属性和值。这个值原本就是用来描述随机现象的发生频率,现在可以来验证概率能否描述频率,这对概率论的自洽性非常重要。
1.1.1 弱大数定律
概率就是事件到实数的映射,一个事件的概率\(p\)应当与大量重复试验中事件出现频率\(\dfrac{\mu_n}{n}\)接近。那什么是接近?怎么度量这个接近?频率序列是一个无限的随机变量序列,说它接近\(p\),比较直观的定义当然是类似极限的定义,即对任意\(\varepsilon>0\),都要有式(1)成立。这个现象被称为伯努利大数定律,它标志着大数定律研究的开始,后续的研究都始于这里。
\[\lim\limits_{n\to\infty}P\left\{\left|\dfrac{\mu_n}{n}-p\right|<\varepsilon\right\}=1\tag{1}\]
从随机变量的角度看,频率其实是\(n\)个独立伯努利变量的平均值,我们自然想把大数定律推广到独立同分布随机变量的平均值,看它是不是接近分布的期望。甚至更一般地,可以讨论任意随机变量序列\(\xi_1,\xi_2,\cdots\),看它们的平均值是不是接近平均期望(式(2))。
\[\lim\limits_{n\to\infty}P\left\{\dfrac{1}{n}\sum\limits_{k=1}^n|\xi_k-E\xi_k|<\varepsilon\right\}=1\tag{2}\]
对此,切比雪夫证明了:当\(\xi_i\)两两不相关,且方差一致有界时有式(2)成立,它被称为切比雪夫大数定律。证明中首次应用了切比雪夫不等式,从此矩不等式成为研究大数定律的重要手段。该定律有两个简单的变形,一个是独立不同伯努利分布下的泊松大数定律,另一个是只需条件\(D(\sum\xi_k)/n^2\to 0\)的马尔科夫大数定律,这些证明都很简单,请自行完成。
在独立同分布的场合,辛钦大数定律甚至不要求方差存在,这进一步放宽了大数定律的条件,它在数理统计中非常重要。证明需要用到著名的连续性定理,大概是说如果分布函数收敛于另一个分布函数,则它们的特征函数也收敛于特征函数。论证中还要用到特征函数与分布函数的唯一确定性,特征函数的威力由此可见一斑。
1.1.2 强大数定律
对于式(1)的定义,应该没有太多的异议和怀疑,但仔细看式(2),有个地方值得我们商讨。式中对某个表达式取了概率,一向严格的你不禁要问:这个概率对应的事件是什么?它的样本空间是什么?两个随机变量能随意地加减吗?运算的意义是什么?这个思考是非常必要的,而且也是对概率论的认识的一次提升,由直观数学向严格的分析数学进行转变。更具体地,我们是要严格定义随机变量序列\(\{\xi_n\}\)收敛于另一个随机变量\(\xi\)。
判断收敛离不开运算和度量,但要使得运算\(\xi_n-\xi\)有意义,必须是\(\xi_n,\xi\)来自同一个概率空间。这样来看,不等式\(|\xi_n(\omega)-\xi(\omega)|<\varepsilon\)就有了确定的意义,它表示满足条件的样本点,且所有这样的样本点可以组成事件(考虑联合分布)。对这样的事件就可以用概率度量,因此我们就有了式(3)随机变量序列收敛的定义,它也叫\(\{\xi_n\}\)以概率收敛于\(\xi\),式(1)就是依概率收敛的例子。
\[\forall(\varepsilon>0),\;\lim\limits_{n\to\infty}P\left\{\left|\xi_n(\omega)-\xi(\omega)\right|<\varepsilon\right\}=1\tag{3}\]
有了这个严谨的定义之后,我们进一步研究随机变量收敛。随机变量虽然叫“变量”,但它的特性更像是一个“函数”,而函数列的收敛与数列的收敛有一个很大的不同,那就是关于一致收敛。依概率收敛本质上就是一般的“数列收敛”,它只考察单个随机变量\(\xi_n\)与\(\xi\)的接近程度,但并没有考虑在每个样本点的收敛情况以及其一致性。我们希望的自然是在每个样本点都一致收敛,换个说法就是:一致收敛的样本点集的概率为\(1\)。这样的收敛性可以表示为式(4),用纯集合的语言一般写作式(5),因此这种收敛也叫以概率1收敛。
\[\forall(\varepsilon>0),\;\lim\limits_{k\to\infty}P\left\{\bigcap_{n=k}^{\infty}\left|\xi_n(\omega)-\xi(\omega)\right|<\varepsilon\right\}=1\tag{4}\]
\[P\left\{\lim_{n\to\infty}\xi_n=\xi\right\}=P\left\{\bigcap_{m=1}^{\infty}\bigcup_{k=1}^{\infty}\bigcap_{n=k}^{\infty}\left(|\xi_n-\xi|<\dfrac{1}{m}\right)\right\}=1\tag{5}\]
不难证明,以概率1收敛是比以概率收敛更强的条件,它真正表示了“处处收敛”。在这样的收敛定义下,把无穷伯努利实验做为样本空间,博雷尔重新讨论了伯努利实验的大数定律,得到了式(6)的强大数定律。这是对频率稳定性的更强证据,在偶然性中发现了必然性,在概率论史上有重要意义。接下来科尔莫戈洛夫对独立同分布的随机变量序列,证明了式(7),还找到了式(7)对独立随机变量序列成立的充分条件:\(\sum\dfrac{D\xi_k}{k^2}\)收敛,它们都被称为科尔莫戈洛夫强大数定律。
\[P\left\{\lim\limits_{n\to\infty}\dfrac{\mu_n}{n}=p\right\}=1\tag{6}\]
\[P\left\{\lim\limits_{n\to\infty}\dfrac{1}{n}\sum\limits_{i=1}^n(\xi_i-E\xi_i)=0\right\}=1\tag{7}\]
1.2 中心极限定理
大数定律集中讨论了随机变量\(\xi_1,\xi_2,\cdots\)平均值的收敛情况,现在来进一步研究随机变量之和本身的分布特点。我们知道,要研究分布特点,最好先将方差统一为\(1\),为此我们还得假设随机变量是两两不相关的,从而可以像式(8)那样将其标准化。
\[\zeta_n=\dfrac{\mu_n-np}{\sqrt{npq}};\;\zeta_n=\dfrac{\sum\limits_{i=1}^n(\xi_i-E\xi_i)}{\sqrt{\sum\limits_{i=1}^nD\xi_i}}\tag{8}\]
最早由棣莫弗和拉普拉斯分别对\(p=\dfrac{1}{2}\)和\(p\ne\dfrac{1}{2}\)时的伯努利试验进行讨论,得到了式(9)的棣莫弗-拉普拉斯极限定理。这个结论如此地迷人,对它的研究长达两个世纪,故也称中心极限定理。后来Lindeberg使用连续定理,证明了式(9)在独立同分布场合也成立,这个结论对数理统计非常重要。
\[\lim\limits_{n\to\infty}P\left\{\zeta_n<x\right\}=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^xe^{-\frac{t^2}{2}}\,\text{d}t\tag{9}\]
中心极限定理还有其它更弱的成立条件,但都很复杂,这里暂且不谈。式(9)中的分布称为正态分布,它是另一个非常普遍的“原子分布”,当一个随机变量受很多因素的影响,但每个因素的影响又不大时,这个随机变量往往就服从正态分布。
2. 正态分布
在中心极限定理中,我们才迟迟地提到正态分布,主要是缺少它并不影响对初等概率的讨论。但正态分布又的确是非常常见和重要的分布,这里对它在做一些扩展讨论,顺便也是对基础概念的一次复习。
2.1 一元正态分布
正态分布主要用于描述误差分布,即随机变量的概率以某个值为中心向两边递减,并且是足够光滑的。但这样的性质太过平凡,为什么一定要是正太分布呢?我们需要其它的条件来得到更多的细节。既然描述的是误差,这个分布应该有这样一个性质:对任意的多次测量结果\(x_1,x_2,\cdots,x_n\),均值\(\bar{x}\)总是最好的接近。这里的“任意”既表示\(x_i\)可以为所有可能值,也表示对所有正整数\(n\)都成立。这个条件虽然合理,但看起来非常苛刻,下面就来尝试一下,看满足条件的分布是否存在。
另一方面,“最好的接近”需要用数学语言描述出来,设分布的密度函数是\(p(x)\),则式(10)左的似然函数应该在\(\bar{x}\)处取到最大值。关于似然函数,以后再数理统计中再详细介绍,这里单拎出这个式子也不违反直观。下面为了简化计算,用\(\ln\,L(x)\)来代替讨论,也就是说式(10)右成立,整理后有式(11)。提醒一下,式(11)应该对任意\(x_i\)和\(n\)都成立。
\[L(x)=\prod\limits_{i=1}^np(x_i-x)\;\Rightarrow\;[\ln\,L(x)]'|_{x=\bar{x}}=0\tag{10}\]
\[g(x)=\dfrac{p'(x)}{p(x)}\;\Rightarrow\;\sum\limits_{i=1}^ng(x_i-\bar{x})=0\tag{11}\]
当\(n=1\)时,只能得到\(p'(0)=0\),\(n=2\)时也只能得到\(g(x)\)的对称性,结论都太过平凡。当\(n=3\)时,由于\(x_1-\bar{x},x_2-\bar{x}\)的任意性,可以得到恒等式(12)左,进而得到式(12)右。注意,当\(n>3\)时,也是得到类似式(12)左的表达式,因此\(g(x)\)存在且只有形式\(ax\)。继续还原,容易得到式(13),由密度函数的积分可求出\(K\),最终得到的便是一元正态分布。注意它的中心为\(0\),故式(10)对中心非零的正态分布不成立,这是由于式(10)的性质就是针对误差的。
\[g(x)+g(y)=g(x+y)\;\Rightarrow\;g(x)=ax\tag{12}\]
\[\ln\,p(x)=\frac{a}{2}x^2+b\;\Rightarrow\;p(x)=Ke^{\frac{a}{2}x^2}\tag{13}\]
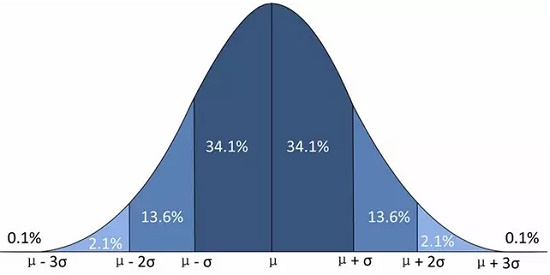
如果把中心也考虑在内,式(14)就是一般的正态分布,简记为\(N(\mu,\sigma^2)\)。容易验证,\(\mu\)是它的数学期望,而\(\sigma^2\)是它的方差,正态分布的图像如下。特别地,\(N(0,1)\)称为标准正态分布,其对应的密度函数和分布函数如式(15)。
\[p(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\tag{14}\]
\[\varphi(x)=\dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}};\;\;\varPhi(x)=\int_{-\infty}^x\varphi(y)\,\text{d}y\tag{15}\]
式(16)验证了\(N(0,1)\)的规范性,这个证明思想可用于计算式(13)中的\(K\)。可以求得正态分布的特征函数是式(17),当\(\mu=0\)时,易知正态分布关于\(\sigma^2\)具有再生性,即如果\(\xi_i\sim N(0,\sigma_i^2)\),则有\(\xi_1+\xi_2\sim N(0,\sigma_1^2+\sigma_2^2)\)。
\[\left(\int_{-\infty}^{+\infty}\varphi(x)\,\text{d}x\right)^2=\dfrac{1}{2\pi}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-\frac{x^2+y^2}{2}}\,\text{d}x\text{d}y=\dfrac{1}{2\pi}\int_0^{\infty}\int_{0}^{2\pi}r\,\text{d}r\text{d}\varphi=1\tag{16}\]
\[f_{\xi}(t)=e^{i\mu t-\frac{1}{2}\sigma^2t^2}\tag{17}\]
2.2 多元正态分布
以上一元正态分布仅受一个维度因素的影响,现在假设某个随机变量受\(n\)个维度的影响,简单起见,设每个维度都是独立的随机变量\(\eta_i\sim N(0,1)\)。可知,随机向量\(\overrightarrow{\eta}=(\eta_1,\cdots,\eta_n)\)的密度为式(18)。函数这样的多元正态分布是平凡的,但对它进行简单的线性变换,便得到一般的多元正态分布,这里的顺序与教材相反。
\[p(\overrightarrow{y})=\dfrac{1}{(2\pi)^{\frac{n}{2}}}e^{-\frac{1}{2}\parallel\overrightarrow{y}\parallel^2} \tag{18}\]
现实中的观察角度往往是\(\eta_i\)的线性组合(式(19)),由特征数的再生性可知\(\xi\sim N(0,\sum a_i^2)\),即每个线性角度看都是正态分布。假设取\(n\)的个线性无关的\(\xi_j\),且有\(\overrightarrow{\xi}=\overrightarrow{\eta}A\),由线性变换的结论可知有式(20)。如果记矩阵\(\varSigma=A^TA\),并加入中心\(\overrightarrow{\mu}\),便得到一般多元正态分布的表达式(21)。
\[\xi=\sum_{i=1}^na_i\eta_i\;\Rightarrow\;f_{\xi}(t)=\prod\limits_{i=1}^ne^{-\frac{1}{2}a_i^2t^2}\tag{19}\]
\[p(\overrightarrow{x})=\dfrac{1}{(2\pi)^{\frac{n}{2}}|A|}\exp\{-\frac{1}{2}\overrightarrow{x}(A^TA)^{-1}\overrightarrow{x}^T\}\tag{20}\]
\[p(\overrightarrow{x})=\dfrac{1}{(2\pi)^{\frac{n}{2}}|\varSigma|^{\frac{1}{2}}}\exp\{-\frac{1}{2}(\overrightarrow{x}-\overrightarrow{\mu})\varSigma^{-1}(\overrightarrow{x}-\overrightarrow{\mu})^T\}\tag{21}\]
式(22)计算了\(\xi_i,\xi_j\)的协方差,不难发现,它正是\(\varSigma[i,j]\),为此\(D\overrightarrow{\xi}=\varSigma=\{\sigma_{ij}\}\)也称为协方差矩阵。由式(23)可知协方差矩阵为正定的(随机变量线性相关才取\(0\)),反之对任意的正定对称矩阵\(\varSigma\),由线性代数的知识,可将分布(21)转化为标准式(18)。这就说明,可以对任意正定对称矩阵\(\varSigma\),定义式(22)为多元正态分布,记作\(N(\overrightarrow{\mu},\varSigma)\)。
\[\sigma_{ij}=E(\xi_i\xi_j)=E\left(\sum\limits_k a_{ik}\xi_k\cdot\sum\limits_k a_{jk}\xi_k\right)=\sum\limits_k a_{ik}a_{jk}\tag{22}\]
\[\sum\limits_{i,j}\sigma_{ij}t_it_j=E\left[\sum\limits_{i=1}^nt_i(\xi_i-E\xi_i)\right]^2\geqslant 0\tag{23}\]
同样利用线性变换,也能求得多元正态分布的特征函数(24),它和多元正态分布互相确定。把中心设为\(0\)后,利用特征函数可以得到更多有用的结论。比如任意子空间\(\overrightarrow{\xi'}=(\xi_1,\cdots,\xi_m)\)的分布都是正态分布,协方差矩阵正好取对应子矩阵,特别地,边界分布\(\xi_i\)是正态分布\(N(\mu_i,\varSigma[i,i])\)。
\[f(\overrightarrow{t})=\exp\{\text{i}\overrightarrow{\mu}\overrightarrow{t}^T-\frac{1}{2}\overrightarrow{t}\varSigma\overrightarrow{t}^T\}\tag{24}\]
多元正态分布的线性本质将独立性和不相关性统一了起来,因为对于互不相关的正态变量,协方差矩阵为对角矩阵,由特征函数的形式特点知变量是相互独立的。一般地还有,对随机正态分布\(\overrightarrow{\xi}=(\overrightarrow{\xi}_1,\overrightarrow{\xi}_2)\),\(\overrightarrow{\xi}_1,\overrightarrow{\xi}_2\)相互独立的充要条件是:对应的对应的协方差矩阵\(\varSigma_{12}=0\)。更本质地,从式(22)可以看出,正态变量独立的充要条件是:对应线性系数(式(19))正交。
对于正态向量\(\overrightarrow{\xi}_1,\overrightarrow{\xi}_2\),由上面的讨论和简单的矩阵运算,可将变换为互相独立的向量\(\overrightarrow{\zeta}_1,\overrightarrow{\zeta}_2\)。当\(\overrightarrow{\xi}_1\)确定时,由独立性知\(\overrightarrow{\zeta}_2\)的条件分布不变,仍然是\(N(0,\varSigma_{22}-\varSigma_{21}\varSigma_{11}^{-1}\varSigma_{12})\)(通过式(25)计算)。再根据式(25)知\(\overrightarrow{\xi}_2\)的条件概率是\(\overrightarrow{\zeta}_2\)的一个偏移,加上中心后便得到条件概率\(\overrightarrow{\xi}_2|\overrightarrow{\xi}_1\)(式(26))。特别地,对二元正态分布有式(27),注意\(\varSigma_{12}=\rho\sigma_1\sigma_2\)。
\[\overrightarrow{\zeta}_1=\overrightarrow{\xi}_1;\;\;\overrightarrow{\zeta}_2=-\overrightarrow{\xi}_1\varSigma_{11}^{-1}\varSigma_{12}+\overrightarrow{\xi}_2\tag{25}\]
\[\overrightarrow{\xi}_2|\overrightarrow{\xi}_1\sim N\left(\overrightarrow{\mu}_2+(\overrightarrow{\xi}_1-\overrightarrow{\mu}_1)\varSigma_{11}^{-1}\varSigma_{12},\varSigma_{22}-\varSigma_{12}\varSigma_{11}^{-1}\varSigma_{21}\right)\tag{26}\]
\[\xi_2|\xi_1\sim N\left(\mu_2+\rho\dfrac{\sigma_2}{\sigma_1}(x-\mu_1),\;\sigma_2^2(1-\rho^2)\right)\tag{27}\]
【全篇完】


 浙公网安备 33010602011771号
浙公网安备 33010602011771号