【初等概率论】 02 - 条件概率和随机变量

　　概率空间是事先给定的，其中样本空间是定义的基础，事件及其概率是我们讨论的对象。那么面对一个给定的概率空间，我们要讨论一些什么问题呢？事件与概率是绑定在一起的，故应把注意力放在事件域上，本篇从两个角度考察事件概率：条件概率和随机变量，它们是概率论中非常基础的概念。

1. 条件概率

1. 1 定义和性质

　　对于整个事件域，我们不光要知道每个事件的概率，还要知道事件之间的关系。具体讲就是，如果事件\(A\)发生了，事件\(B\)会是什么情况呢？当然这里所说的情况还是指“概率”，不过这时的样本空间已经发生了变化，由\(\Omega\)变成了\(A\)，自然原本的事件也都变成了与\(A\)的交集，比如事件\(B\)对应到事件\(AB\)。我们自然希望新事件域上的概率与之前的“兼容”，可以以\(P(A)\)作为基准，以\(P(AB)\)作为“可能性”的度量，容易构造出新的概率为\(\dfrac{P(AB)}{P(A)}\)。这样的定义不光符合直觉，还容易证明是符合概率的三条要求的。数学上，把式（1）定义为事件\(B\)关于事件\(A\)的条件概率，条件概率生成的概率空间具有一般概率空间的所有性质。

\[P(B|A)=\dfrac{P(AB)}{P(A)}\tag{1}\]

　　先把目光放在概率空间的转移上，可以把\(\Omega\)上对应的称为先验概率空间，而把\(A\)上对应的称为后验概率空间。前者表示在没有其它条件下的概率，而后者表示获得了信息\(A\)后的概率，这也是条件概率名称的由来。条件概率不仅揭示了事件概率随条件的变化，本质上更是揭示了事件之间的关联。如果后验概率与先验概率不同，则表示事件\(A\)与其它事件之间有一定关系，至于如何度量这个关联，以后会具体讨论。

　　在很多时候，后验概率反而更容易获取，这时把式（1）改写成式（2）会更有意义，它可以求得“局部”的先验概率。这个思想容易扩展成式（3）的乘法公式，它将复杂的概率分解成了多层简单的概率，在实际计算中非常有用。

\[P(AB)=P(A)P(B|A)\tag{2}\]

\[P(A_1A_2\cdots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1A_2\cdots A_{n-1})\tag{3}\]

　　式（2）得到的是事件\(B\)在条件\(A\)下的片段，如果样本空间\(\Omega\)可以被分割为可数个互斥条件\(A_i\)，并且\(B\)在每个条件下的概率都容易求得，则不难得到\(B\)的完整先验概率。式（4）被称为全概率公式，它经常被用在事件可以按条件分类的场景，是也是一个常用的方法。

\[P(B)=\sum_{i=1}^{\infty}P(A_iB)=\sum\limits_{i=1}^{\infty}P(A_i)P(B|A_i)\tag{4}\]

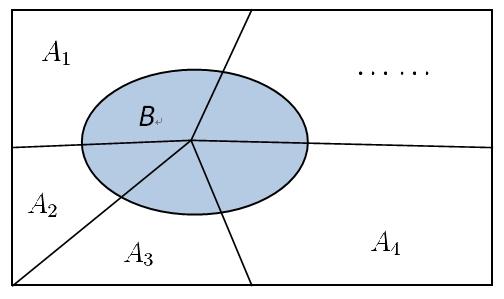
　　继续观察全概率模型，样本空间被条件\(A_i\)划分，而在每个条件下事件\(B\)发生概率也是清楚的。试想如果事件\(B\)的确发生了，如何计算条件\(A_i\)发生的概率\(P(A_i|B)\)？这是一个后验概率的计算，只不过把条件与结果的顺序颠倒了。利用式（5）不难得到式（6），它就是著名的贝叶斯公式。要想在观察值\(B\)下估算实际的值，可事先统计实际值的分布、以及对每个实际值的可能观察值。贝叶斯公式为信息判断提供了一种便捷可靠的途径，在工业上被广泛应用。

\[P(B)P(A_i|B)=P(A_iB)=P(A_i)P(B|A_i)\tag{5}\]

\[P(A_i|B)=\dfrac{P(A_i)P(B|A_i)}{P(B)}=\dfrac{P(A_i)P(B|A_i)}{\sum\limits_{j=1}^{\infty}P(A_j)P(B|A_j)}\tag{6}\]

1.2 统计独立性

　　前面说过，条件概率反应了事件之间的关系，当条件概率\(P(B|A)\)与先验概率\(P(B)\)不相同时，可以认为条件\(A\)对事件\(B\)造成了影响。这里先讨论简单的情景，即条件\(A\)并没有对事件\(B\)的概率造成影响，这时有\(P(B|A)=P(B)\)。展开条件概率得到它的等价表达式（7），该式中\(A,B\)的关系是对等的，它更适合用来表示“相互”的关系。

　　对于满足式（7）的事件\(A,B\)，一般称之为统计独立的，或简称独立的。其实并不能说独立的两个事件是“无关”的，这里的独立仅适用于统计概率值的关系，这个认识非常重要，它也正是数学严谨性的体现，每个概念都有它明确的所指。“无关”是个很宽泛的概念，在这里是能包含统计独立性的。因此在现实使用中，如果不需要严格论证，就可以把那些明显“无关”的事件看成是独立的，比如两次互不干扰的随机试验。

\[P(AB)=P(A)P(B)\;\Leftrightarrow\;P(B|A)=P(B)\;\Leftrightarrow\;P(A|B)=P(A)\tag{7}\]

\[P(A_1A_2\cdots A_n)=P(A_1)P(A_2)\cdots P(A_n)\tag{8}\]

　　统计独立性可以简化很多问题的计算，当事件独立时，联合事件的概率可以直接由各个事件概率相乘得到（式（8））。另外容易证明，如果事件\(A,B\)独立，则\(\bar{A},\bar{B}\)、\(\bar{A},B\)、\(A,\bar{B}\)也是独立的，这个结论使得独立性更方便使用。

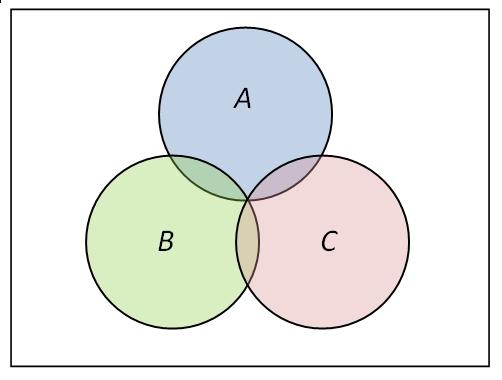
　　独立性作为事件间的一种“关系”，它有没有传递性呢？你画个文氏图，很容易找出反例，即独立性是与“两者”紧相连的，与第三者并无关联。更甚者，如果你要定义三个事件之间“相互独立”，光有两两独立也是不够的。所谓多个事件的相互独立，自然是想任何事件（或联合事件）都统计独立于其它事件（或联合事件），光有两两独立是不够的。举个三个事件下的反例就足够了，图中\(A,B,C\)两两独立，但显然\(A\)与\(BC\)不独立。\(n\)个事件相互独立的条件是式（9）成立，其中\(A_{i_1},\cdots,A_{i_m}\)是对任意\(m\)任意选取的\(m\)个不同事件。

\[P(A_{i_1}A_{i_2}\cdots A_{i_m})=P(A_{i_1})P(A_{i_2})\cdots P(A_{i_m}),\;(2\leqslant m\leqslant n)\tag{9}\]

2. 随机变量

2.1 分布函数

　　概率空间的模型好像很难进一步讨论下去，主要原因是样本空间是一般性的集合。如果把样本空间特殊化成数集，概率就能和函数联系起来，处理起来就能方便得多，而且可以直接利用实变函数的结论。另一方面，实际应用中的样本空间往往就是一个整数集或实数集，这就有了充分的理由来研究实数样本空间的概率问题。不过统一的论证需要测度论的知识，这里仅以离散模型和连续模型为例，阐明随机变量的概念。

　　先是将样本点对应成实数，也就是说存在\(\Omega\to\Bbb{R}\)上的映射\(\xi(\omega)\)。新的样本空间中，我们自然以一维博雷尔域\(\mathscr{B}_1\)为事件域。要使得原来的概率在新事件域上仍然是概率，还得要求任何博雷尔点集\(B\)的原像是一个事件，即满足式\(\{\omega:\xi(\omega)\in B\}\in\scr{F}\)，而\(B\)的概率则应是\(P\{\xi(\omega)\in B\}\)。这个条件虽然重要，但在实际中往往都是成立的，故以后直接使用新的概率空间。

　　映射\(\xi(\omega)\)的值是实数，它随着\(\omega\)变化，并且还带有概率的属性，一般也把它称为随机变量，简写为\(\xi\)，仔细品味\(\xi\)的含义对理解随机变量很重要。我们知道，一维博雷尔域可以由所有的开区间\((-\infty,a)\)生成，因此如果能描述所有\((-\infty,a)\)上的概率，也就完整描述了随机变量的概率分布。式（10）中的实函数便满足要求，它被称为随机变量\(\xi\)的分布函数，也说成\(\xi\)服从分布\(F(x)\)，简记为\(\xi\sim F(x)\)。

\[F(x)=P\{\xi(\omega)<x\}\tag{10}\]

　　容易证明分布函数满足以下三个性质，它们与概率的三条性质一一对应。实变函数中还能证明：任何满足这三个条件的函数，都是某个随机变量的分布函数，并且随机变量和分布函数相互唯一确定。

　　（1）单调性：\(a<b\,\Rightarrow\, F(a)<F(b)\)；

　　（2）规范性：\(\lim\limits_{x\to-\infty}F(x)=0\)，\(\lim\limits_{x\to+\infty}F(x)=1\)；

　　（3）左连续性：\(F(x^-)=F(x)\)。

　　分布函数为概率空间提供了统一的描述，使得分析的工具更容易使用，但这里我们不进行分析讨论，故还是分成离散和连续两种情况直接讨论。离散随机变量的分布函数是一个跳跃函数，直接讨论它的分布函数\(p(\xi=x_i)\)会更方便直观。对于连续随机变量的分布函数，一般假定它是光滑的，即存在连续导函数\(p(x)=F'(x)\)。仔细思考导数的含义，你同样会明白，\(p(x)\)并不是\(x\)处的概率，它表示\(x\)附近的“平均概率”或者“概率密度”，因此\(p(x)\)也称为\(\xi\)的密度函数，显然有式（11）成立。

\[F(x)=\int_{-\infty}^xp(y)\,\text{d}y\tag{11}\]

2.2 随机变量的函数

　　现在我们已经进入变量和函数的世界，有个很自然的问题是，如果随机变量\(\eta\)满足\(\eta=g(\xi)\)，则如何用\(\xi\)的分布函数\(F(x)\)表示\(\eta\)的分布函数？这个问题不难，直接用定义有式（12），但可惜它无法化简，因为非常依赖于\(g(x)\)的特性。

\[G(y)=P\{\eta<y\}=P\{g(\xi)<y\}=\int_{g(x)<y}p(x) \text{d}x\tag{12}\]

　　但在一些特殊情景下，式（12）还可以进一步化简。比如假设\(g(x)\)是单调递增的，则容易有\(G(y)=F(g^{-1}(y))\)。有趣的是，如果\(F(x)\)本身是单调的，则易知随机变量\(\eta=F(\xi)\)的分布函数是\(G(y)=y\)，它是\([0,1]\)上的均匀分布。这就启发我们，对任何单调的分布函数\(F(x)\)，我们都可以构造出它的随机变量\(F^{-1}(\eta)\)，而需要的只是一个\([0,1]\)上的均匀分布。这个结论的条件还可以放宽，有兴趣的自行研究，它被称为随机变量的存在定理。

　　当\(\xi\)有密度函数\(p(x)\)，而\(g(x)\)有连续导函数时，容易证明\(\eta\)的密度函数\(q(y)\)满足式（13）。如果你理解密度函数的意义，其实式（13）有着很直观的解释，就是表示斜率对密度的影响。根据这个思想，如果\(g(x)\)的导函数分段连续，可以将公式（13）应用在每个分段中，然后每段的密度函数相加即可。

\[q(y)=p[g^{-1}(y)]\cdot\left|[g^{-1}(y)]'\right|\tag{13}\]

　　当然还可以讨论多元函数的随机变量\(\eta=g(\xi_1,\cdots,\xi_n)\)，但一般情况下也很难得到简单的分布函数，只能针对特殊情况分别讨论。比如当\(\xi_1,\xi_2\)相互独立时，你可以求得\(\eta=\xi_1+\xi_2\)的分布函数（14）。它被称为卷积公式，卷积的概念在数学里非常常见。还可以求得\(\eta=\xi_1/\xi_2\)的分布函数（15），该式在数理统计中比较有用。

\[\eta=\xi_1+\xi_2\;\Rightarrow\;q(y)=\int_{-\infty}^{+\infty}p_1(y-u)p_2(u)\,\text{d}u\tag{14}\]

\[\eta=\dfrac{\xi_1}{\xi_2},\;(\xi_2>0)\;\Rightarrow\;q(y)=\int_{-\infty}^{+\infty}up_1(yu)p_2(u)\,\text{d}u\tag{15}\]

　　• 设\(\eta,\zeta\)分别是独立随机变量\(\xi_1,\cdots,\xi_n\)中的最大值和最小值，试求\(\eta,\zeta,\eta-\zeta\)的分布函数。

2.3 随机向量

　　有时候，随机事件的值是一个多维向量\(\overrightarrow{\xi}=(\xi_1,\xi_2,\cdots,\xi_n)\)，它被称为随机向量或\(n\)维随机变量。容易定义\(\overrightarrow{\xi}\)的（联合）分布函数如式（16），它在每一维都是递增的。但在每一维都递增的函数（同时满足分布函数其它特点），不一定是分布函数。拿二维空间为例，只有满足空间上的递增性（而不是单个维度），才能成为分布函数，因此还必须有式（17）成立。

\[F(x_1,x_2,\cdots,x_n)=P\{\xi_1<x_1,\xi_2<x_2,\cdots,\xi_n<x_n\}\tag{16}\]

\[P\{a_1\leqslant\xi_1<b_1,a_2\leqslant\xi_2<b_2\}=F(b1,b_2)-F(a_1,b_2)-F(b_1,a_2)+F(a_1,a_2)\geqslant 0\tag{17}\]

　　随机向量也可以定义密度函数，而且在每一维都有式（18）的边际分布（分别是离散和连续）。但同样的边际分布却可能有不同的分布函数，主要是因为每一维的随机变量之间可能不是独立的。这就为我们提供了另一个视角看随机向量，它是讨论随机变量关系的一个很好的场所，就像条件概率\(P(B|A)\)要借助\(P(AB)\)定义一样。

\[p_1(x_i)=\sum\limits_j p(x_i,y_j);\;\; p_1(x)=\int_{-\infty}^{+\infty}p(x,y)\,\text{d}y \tag{18}\]

　　不管是离散还是连续场景，式（19）定义的\(\xi\)关于\(\eta\)的条件分布都是合理的。可以把条件分布的概率分布（或密度函数）简写为\(p(x|y)\)，容易推导出它有表达式（20）（离散和连续）。自然地，满足式（21）的随机变量被称为相互独立的，它们的分布函数和密度函数可以拆分为边际分布之积，且由边际分布唯一确定（式（22）。

\[P\{\xi<x|\eta=y\}=\lim\limits_{\varDelta y\to 0}P\{\xi<x|y\leqslant\eta<y+\varDelta y\}\tag{19}\]

\[p(x_i|y_j)=\dfrac{p(x_i,y_j)}{p_2(y_j)};\;\;p(x|y)=\dfrac{p(x,y)}{p_2(y)}\tag{20}\]

\[P\{\xi_1<x_1,\cdots,\xi_n<x_n\}=P\{\xi_1<x_1\}\cdots P\{\xi_n<x_n\}\tag{21}\]

\[F(x_1,\cdots,x_n)=F_1(x_1)\cdots F_n(x_n);\;\;p(x_1,\cdots,x_n)=p_1(x_1)\cdots p_n(x_n)\tag{22}\]

　　最后再来看随机向量的变换\(\overrightarrow{\eta}=g(\overrightarrow{\xi})\)，利用微积分中多元函数变换的结论，如果\(\overrightarrow{\eta},\overrightarrow{\xi}\)的维度相同且存在逆函数，则有式（23）成立，其中\(J\)是向量变换的雅克比行列式。这个结论可以对随机向量进行变换，从而得到更便于处理的分布（比如各维度相互独立）。还有一个作用是计算随机变量的多元函数\(\eta_1=g(\xi_1,\cdots,\xi_n)\)的分布，步骤是先添加\(n-1\)个辅助的多元函数，求得联合密度函数（23）后再求\(\eta_1\)的边际分布。

\[q(y_1,\cdots,y_n)=p(x_1(y_1,\cdots,y_n),\cdots,x_n(y_1,\cdots,y_n))\cdot |J|\tag{23}\]