剑指Offer面试题:22.二叉搜索树的后序遍历序列
一、题目:二叉搜索树的后序遍历序列
题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。
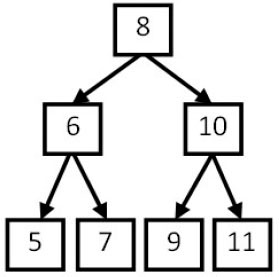
例如在下面的一颗二叉搜索树中,输入数组{5,7,6,9,11,10,8},则返回true,因为这个整数序列是下图二叉搜索树的后序遍历结果。如果输入的数组是{7,4,6,5},由于没有哪棵二叉搜索树的后序遍历的结果是这个序列,因此返回false。
二、解题思路
2.1 核心步骤
在后序遍历得到的序列中,最后一个数字是树的根结点的值。数组中前面的数字可以分为两部分:第一部分是左子树结点的值,它们都比根结点的值小;第二部分是右子树结点的值,它们都比根结点的值大。
因此,我们可以总结出算法步骤:
Step1.通过取出序列最后一个元素得到二叉搜索树的根节点;
Step2.在二叉搜索树中左子树的结点小于根结点,因此可以遍历一次得到左子树;
Step3.在二叉搜索树中右子树的结点大于根结点,因此可以继续遍历后序元素得到右子树;
Step4.重复以上步骤递归判断左右子树是不是二叉搜索树,如果都是,则返回true,如果不是,则返回false;
2.2 代码实现
public static bool VerifySquenceOfBST(int[] sequence, int length) { if (sequence == null || length <= 0) { return false; } int root = sequence[length - 1]; int i = 0; // 在二叉搜索树中左子树的结点小于根结点 for (; i < length - 1; i++) { if (sequence[i] > root) { break; } } // 在二叉搜索树中右子树的结点大于根结点 int j = i; for (; j < length - 1; j++) { if (sequence[j] < root) { // 如果找到小于根节点直接返回false return false; } } // 判断左子树是不是二叉搜索树 bool leftIsBST = true; if (i > 0) { leftIsBST = VerifySquenceOfBST(sequence, i); } // 判断右子树是不是二叉搜索树 bool rightIsBST = true; if (j < length - 1) { // C#中无法直接操作指针,在C/C++可以直接传递sequence+i int[] newSequence = sequence.Skip(i).ToArray(); rightIsBST = VerifySquenceOfBST(newSequence, length - i - 1); } return leftIsBST && rightIsBST; }
三、单元测试
3.1 测试用例
// 10 // / \ // 6 14 // /\ /\ // 4 8 12 16 [TestMethod] public void SequenceTest1() { int[] data = { 4, 8, 6, 12, 16, 14, 10 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, true); } // 5 // / \ // 4 7 // / // 6 [TestMethod] public void SequenceTest2() { int[] data = { 4, 6, 7, 5 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, true); } // 5 // / // 4 // / // 3 // / // 2 // / // 1 [TestMethod] public void SequenceTest3() { int[] data = { 1, 2, 3, 4, 5 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, true); } // 1 // \ // 2 // \ // 3 // \ // 4 // \ // 5 [TestMethod] public void SequenceTest4() { int[] data = { 5, 4, 3, 2, 1 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, true); } // 树中只有1个结点 [TestMethod] public void SequenceTest5() { int[] data = { 5 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, true); } // 错误序列 [TestMethod] public void SequenceTest6() { int[] data = { 7, 4, 6, 5 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, false); } // 错误序列 [TestMethod] public void SequenceTest7() { int[] data = { 4, 6, 12, 8, 16, 14, 10 }; bool result = SequenceHelper.VerifySquenceOfBST(data, data.Length); Assert.AreEqual(result, false); } // 错误序列 [TestMethod] public void SequenceTest8() { bool result = SequenceHelper.VerifySquenceOfBST(null, 0); Assert.AreEqual(result, false); }
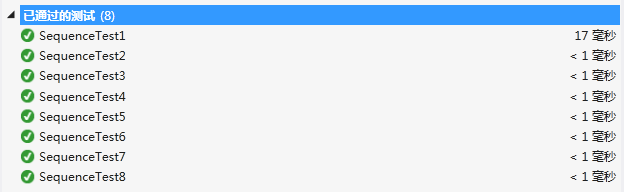
3.2 测试结果


 题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。例如在下面的一颗二叉搜索树中,输入数组{5,7,6,9,11,10,8},则返回true,因为这个整数序列是下图二叉搜索树的后序遍历结果。如果输入的数组是{7,4,6,5},由于没有哪棵二叉搜索树的后序遍历的结果是这个序列,因此返回false。
题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。例如在下面的一颗二叉搜索树中,输入数组{5,7,6,9,11,10,8},则返回true,因为这个整数序列是下图二叉搜索树的后序遍历结果。如果输入的数组是{7,4,6,5},由于没有哪棵二叉搜索树的后序遍历的结果是这个序列,因此返回false。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号