【bzoj4176】Lucas的数论 莫比乌斯反演+杜教筛

题目描述

去年的Lucas非常喜欢数论题，但是一年以后的Lucas却不那么喜欢了。

在整理以前的试题时，发现了这样一道题目“求Sigma(f(i)),其中1<=i<=N”，其中 表示i的约数个数。他现在长大了，题目也变难了。

求如下表达式的值：

 

其中f(ij)表示ij的约数个数。

他发现答案有点大，只需要输出模1000000007的值。

输入

第一行一个整数n。

输出

一行一个整数ans，表示答案模1000000007的值。

样例输入

2

样例输出

8

---

题解

莫比乌斯反演+杜教筛

首先有个神奇的结论：

证明：只考虑质数p，设n=a*p^x，m=b*p^y，那么等式左端p的贡献显然为x+y+1；而等式右边p的贡献为数对(i,j)：(p,1),(p^2,1),...,(p^x,1) , (1,p),(1,p^2),...,(1,p^y) , (1,1)，共x+y+1对，因此命题得证。

然后就有：

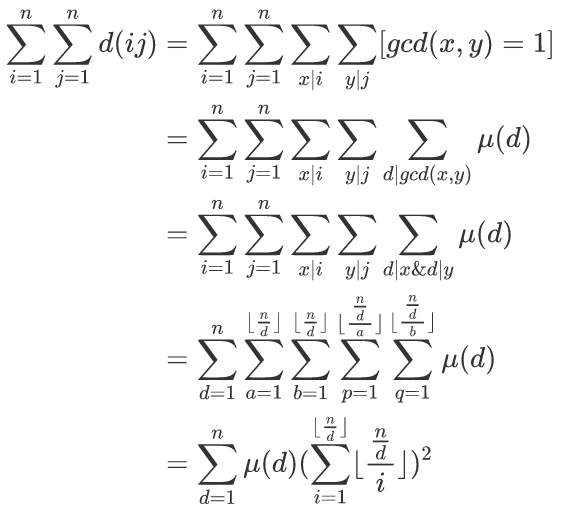
注意到n/d只有O(√n)种取值，因此我们可以枚举这些n/d，找出对应的d的范围，前边的mu(d)求一下前缀和，后面的sigma，由于n/d/i只有O(√n/d)种取值，因此可以用O(√n/d)的复杂度求出。

由于这里面的n值过大，无法直接维护mu的前缀和，因此需要使用杜教筛的方法，参见 bzoj3944

因此总的时间复杂度貌似是O(n^3/4+n^2/3logn)。

#include <cstdio>
#include <map>
#define N 1000010
using namespace std;
#define mod 1000000007
typedef long long ll;
map<ll , ll> f;
map<ll , ll>::iterator it;
ll m = 1000000 , mu[N] , prime[N] , tot , sum[N];
bool np[N];
ll cal1(ll n)
{
	if(n <= m) return sum[n];
	it = f.find(n);
	if(it != f.end()) return it->second;
	ll ans = 1 , i , last;
	for(i = 2 ; i <= n ; i = last + 1) last = n / (n / i) , ans = (ans - (last - i + 1) * cal1(n / i) % mod + mod) % mod;
	return f[n] = ans;
}
ll cal2(ll n)
{
	ll ans = 0 , i , last;
	for(i = 1 ; i <= n ; i = last + 1) last = n / (n / i) , ans = (ans + n / i * (last - i + 1)) % mod;
	return ans * ans % mod;
}
int main()
{
	ll n , i , j , last , ans = 0;
	mu[1] = sum[1] = 1;
	for(i = 2 ; i <= m ; i ++ )
	{
		if(!np[i]) mu[i] = -1 , prime[++tot] = i;
		for(j = 1 ; j <= tot && i * prime[j] <= m ; j ++ )
		{
			np[i * prime[j]] = 1;
			if(i % prime[j] == 0)
			{
				mu[i * prime[j]] = 0;
				break;
			}
			else mu[i * prime[j]] = -mu[i];
		}
		sum[i] = (sum[i - 1] + mu[i] + mod) % mod;
	}
	scanf("%lld" , &n);
	for(i = 1 ; i <= n ; i = last + 1) last = n / (n / i) , ans = (ans + (cal1(last) - cal1(i - 1) + mod) % mod * cal2(n / i)) % mod;
	printf("%lld\n" , ans);
	return 0;
}