浅谈BP神经网络
前言
BP 神经网络是一种多层前馈神经网络(由多层构成,信息从前往后传播,误差从后往前传播)。由输入层、隐藏层和输出层组成。BP 神经网络常用来处理回归、分类、模式识别等问题。
激活函数
BP 神经网络通过激活函数的缩放、拉伸、组合等操作达到拟合函数的目的。激活函数的意义是引入非线性因素。如果没有激活函数,本质上就是在将直线变形,得到的仍是直线,无法拟合复杂的非线性函数。下表是常见的四种激活函数(Sigmoid 受图片限制展示不全):
| 名称 | 图像特点 | 表达式 | 导数 | 图像 |
|---|---|---|---|---|
| ReLU | 折线 | f ( x ) = { x x ≥ 0 0 x < 0 f(x) = \begin{cases}x & x \ge 0 \\0 & x < 0\end{cases} f(x)={x0x≥0x<0 | f ′ ( x ) = { 1 x > 0 不可导 x = 0 0 x < 0 f'(x) = \begin{cases}1 & x > 0\\不可导&x=0 \\0 & x < 0\end{cases} f′(x)=⎩ ⎨ ⎧1不可导0x>0x=0x<0 | 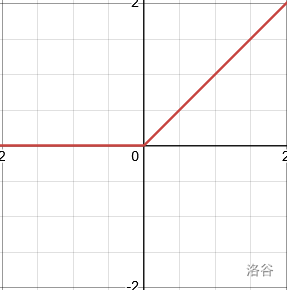 |
| LeakyReLU | 折线 | f ( x ) = { x x ≥ 0 x × α x < 0 f(x) = \begin{cases}x & x \geq 0 \\x\times \alpha & x < 0\end{cases} f(x)={xx×αx≥0x<0 | f ′ ( x ) = { 1 x > 0 不可导 x = 0 α x < 0 f'(x) = \begin{cases}1 & x >0\\不可导&x=0 \\\alpha & x < 0\end{cases} f′(x)=⎩ ⎨ ⎧1不可导αx>0x=0x<0 | 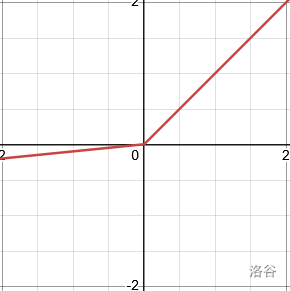 |
| Sigmoid | S 形 | f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1 | f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x)) | 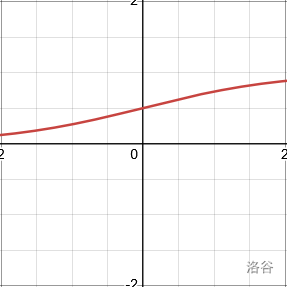 |
| Tanh | S 形 | f ( x ) = e x − e − x e x + e − x f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x | f ′ ( x ) = 1 − f 2 ( x ) f'(x)=1-f^2(x) f′(x)=1−f2(x) | 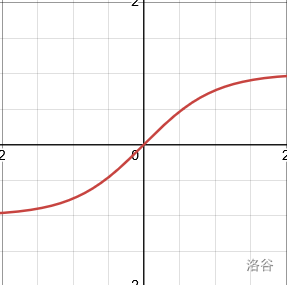 |
虽然 ReLU 和 LeakyReLU 在 x = 0 x=0 x=0 处不可导,但实际应用中,可以把这一点的导数看成 1 1 1( α \alpha α)。
正向传播
下面通过一个简单的例子解释 BP 神经网络正向传播的主要过程:
假设我们需要拟合的函数如下图所示: 原链接
原链接
为了拟合它,我们需要先搞清楚如何将激活函数变形。以 ReLu 为例,设 f ( x ) = max ( 0 , x ) f(x)=\max(0,x) f(x)=max(0,x)。
- 上下平移(紫线): g ( x ) = f ( x ) + a g(x)=f(x)+a g(x)=f(x)+a
- 左右平移(蓝线): g ( x ) = f ( x + a ) g(x)=f(x+a) g(x)=f(x+a)
- 缩放(绿线):
g
(
x
)
=
f
(
a
x
)
g(x)=f(ax)
g(x)=f(ax)
 原链接
原链接
原折线可以表示为 f ( x ) + f ( 2 x − 6 ) + 3 f\left(x\right)+f\left(2x-6\right)+3 f(x)+f(2x−6)+3,如果把它画成图,可能是这样的:
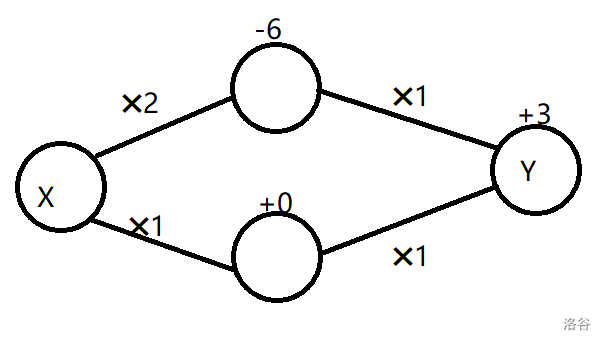
对着上面给的式子 f ( x ) + f ( 2 x − 6 ) + 3 f\left(x\right)+f\left(2x-6\right)+3 f(x)+f(2x−6)+3,不难看懂上图。值得一提,如果你在网上搜索神经网络的示意图,得到的图片大概率也是长这样的。
我们把边上面乘以的数叫做权重,把点上加的数叫做偏置,图上每个圆圈叫做神经元。在实际画图时,一般不画偏置,如果非要画只需要加一个输出 1 1 1 虚拟的点就行了。图上的点按照横向的位置分成三层,这就是输入层、隐藏层和输出层。输入和输出层只有一层,而隐藏层可以有很多层。
把第 i i i 层 j j j 号神经元得到的输入值记作 R i , j R_{i,j} Ri,j,第 i i i 层 j j j 号神经元的输出值记作 V i , j V_{i,j} Vi,j,连接第 i i i 层的 j j j 号神经元和第 i + 1 i+1 i+1 层的 k k k 号神经元的边的权重记作 W i , j , k W_{i,j,k} Wi,j,k,第 i i i 层 j j j 号神经元的偏置记作 B i , j B_{i,j} Bi,j,第 i i i 层的神经元数量记作 N i N_i Ni,激活函数为 f ( x ) f(x) f(x),可以写出正向传播的公式(建议结合上图理解)。
R i , j = ∑ k = 1 N i − 1 V i − 1 , k × W i − 1 , k , j + B i , j V i , j = f ( R i , j ) R_{i,j}=\sum^{N_{i-1}}_{k=1}V_{i-1,k}\times W_{i-1,k,j} + B_{i,j}\\ V_{i,j}=f\left(R_{i,j}\right) Ri,j=k=1∑Ni−1Vi−1,k×Wi−1,k,j+Bi,jVi,j=f(Ri,j)
反向传播
在正向传播中,出现了很多系数,那么系数怎么确定呢?
首先,引入损失函数 L = 1 2 ∑ i = 1 N M ( V M , i − o i ) 2 L=\frac{1}{2}\sum^{N_M}_{i=1} (V_{M,i}-o_i)^2 L=21∑i=1NM(VM,i−oi)2( M M M 是输出层的层数编号, o i o_i oi 表示输出层 i i i 号神经元的预期输出值,由训练数据给出)乘以 1 2 \frac{1}{2} 21 是为了方便后面的计算。
损失函数是关于 BP 神经网络中每一个参数的函数,反向传播的目标就是通过调整系数使得 L L L 尽量的小。在一个复杂的 BP 神经网络中, L L L 也是一个很复杂的函数,它的最小值一般不存在解析解,即无法用公式算出来。此时就要通过迭代的方法求出一个数值解,在 BP 神经网络中,使用梯度下降。
梯度下降
如果我们把 L L L 的图像画出来,可以看成是一座高维的山。调整神经网络参数的过程,就可以看成再这座山上行走的过程。 L L L 的最小值,就对应着这座山的最低点。此时我们能获取到的只有身处的那一点的信息,类比下山的过程,在不知道路时时,该怎么走下山呢?可以寻找最陡峭的方向往下走一步,然后继续寻找最陡峭的方向往下走。这个最陡峭,即函数减小最快的方向就是梯度。
梯度是函数对每个参数求偏导得到的数值组成的向量。如 J ( Θ ) = 3 θ 0 + θ 1 2 − θ 2 J(\boldsymbol{\Theta})=\boldsymbol{3\theta}_0+\boldsymbol{\theta}_1^2-\boldsymbol{\theta}_2 J(Θ)=3θ0+θ12−θ2 的梯度 ∇ J ( Θ ) = ( ∂ J ∂ θ 0 , ∂ J ∂ θ 1 , ∂ J ∂ θ 2 ) = ( 3 , 2 θ 1 , − 1 ) \nabla J(\boldsymbol{\Theta})=\left(\frac{\partial J}{\partial \boldsymbol{\theta}_0},\frac{\partial J}{\partial \boldsymbol{\theta}_1},\frac{\partial J}{\partial \boldsymbol{\theta}_2}\right)=\left(3,2 \boldsymbol{\theta}_1,-1\right) ∇J(Θ)=(∂θ0∂J,∂θ1∂J,∂θ2∂J)=(3,2θ1,−1)。梯度指向的方向是函数增长最快的方向,梯度的反方向是函数减小最快的方向。证明可以看这里。
往梯度的反方向走,实际上就是加上一个与梯度方向相反的向量,于是可以得出梯度下降的公式: θ i = θ i − 1 − η ∇ J ( θ i − 1 ) \boldsymbol{\theta}_i=\boldsymbol{\theta}_{i-1}-\eta \nabla J(\boldsymbol{\theta}_{i-1}) θi=θi−1−η∇J(θi−1)。其中, η \eta η 被称为学习率 / 步长,用来控制梯度下降时行走的距离。为了防止移动太远越过最小值, η \eta η 一般是一个比较小的数(如 0.01 0.01 0.01)。
梯度推导
求梯度的过程需要对每个参数求偏导,这个求偏导的过程可以使用链式法则。链式法则不是本文的重点,不懂的可以自己搜,这里就不讲了。
先看输出层:
∂ L ∂ V M , i = ∂ 1 2 ∑ j = 1 N M ( V M , j − o j ) 2 ∂ V M , i \frac{\partial L}{\partial V_{M,i}}=\frac{\partial \frac{1}{2}\sum^{N_M}_{j=1} (V_{M,j}-o_j)^2}{\partial V_{M,i}} ∂VM,i∂L=∂VM,i∂21∑j=1NM(VM,j−oj)2
当 i ≠ j i\not=j i=j 时, ∂ ( V M , j − o j ) 2 ∂ V M , i = 0 \frac{\partial(V_{M,j}-o_j)^2}{\partial V_{M,i}}=0 ∂VM,i∂(VM,j−oj)2=0,于是原式可以转化为:
∂ 1 2 ( V M , i − o i ) 2 ∂ V M , i = V M , i − o i \frac{\partial \frac{1}{2}\left(V_{M,i}-o_i\right)^2}{\partial V_{M,i}}=V_{M,i}-o_i ∂VM,i∂21(VM,i−oi)2=VM,i−oi
之前加的 1 2 \frac{1}{2} 21 作用就是在这里消去平方求导产生的 × 2 \times2 ×2。
再看其他层:根据链式法则:
∂ L ∂ V i , j = ∑ k = 1 N i + 1 ∂ L ∂ V i + 1 , k × ∂ V i + 1 , k ∂ V i , j \frac{\partial L}{\partial V_{i,j}}=\sum_{k=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,k}}\times \frac{\partial V_{i+1,k}}{\partial V_{i,j}} ∂Vi,j∂L=k=1∑Ni+1∂Vi+1,k∂L×∂Vi,j∂Vi+1,k
设激活函数为 f ( x ) f(x) f(x),将正向传播公式代入:
∂ L ∂ V i , j = ∑ k = 1 N i + 1 ∂ L ∂ V i + 1 , k × ∂ f ( ∑ l = 1 N i V i , l × W i , l , k + B i + 1 , k ) ∂ V i , j = ∑ k = 1 N i + 1 ∂ L ∂ V i + 1 , k × f ′ ( ∑ l = 1 N i V i , l × W i , l , k + B i + 1 , k ) × ∂ ∑ l = 1 N i V i , l × W i , l , k + B i + 1 , k ∂ V i , j \frac{\partial L}{\partial V_{i,j}}=\sum_{k=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,k}}\times \frac{\partial f\left(\sum^{N_{i}}_{l=1}V_{i,l}\times W_{i,l,k} + B_{i+1,k}\right)}{\partial V_{i,j}}\\=\sum_{k=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,k}}\times f'\left(\sum^{N_{i}}_{l=1}V_{i,l}\times W_{i,l,k} +B_{i+1,k}\right)\times \frac{\partial \sum^{N_{i}}_{l=1}V_{i,l}\times W_{i,l,k} +B_{i+1,k}}{\partial V_{i,j}} ∂Vi,j∂L=k=1∑Ni+1∂Vi+1,k∂L×∂Vi,j∂f(∑l=1NiVi,l×Wi,l,k+Bi+1,k)=k=1∑Ni+1∂Vi+1,k∂L×f′(l=1∑NiVi,l×Wi,l,k+Bi+1,k)×∂Vi,j∂∑l=1NiVi,l×Wi,l,k+Bi+1,k
当 l ≠ j l\not=j l=j 时, ∂ V i , l × W i , l , k ∂ V i , j = 0 \frac{\partial V_{i,l}\times W_{i,l,k}}{\partial V_{i,j}}=0 ∂Vi,j∂Vi,l×Wi,l,k=0 于是原式等于:
∑ k = 1 N i + 1 ∂ L ∂ V i + 1 , k × f ′ ( ∑ l = 1 N i V i , l × W i , l , k + B i + 1 , k ) × ∂ V i , j × W i , j , k ∂ V i , j = ∑ k = 1 N i + 1 ∂ L ∂ V i + 1 , k × f ′ ( ∑ l = 1 N i V i , l × W i , l , k + B i + 1 , k ) × W i , j , k \sum_{k=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,k}}\times f'\left(\sum^{N_{i}}_{l=1}V_{i,l}\times W_{i,l,k} +B_{i+1,k}\right)\times \frac{\partial V_{i,j}\times W_{i,j,k}}{\partial V_{i,j}}\\=\sum_{k=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,k}}\times f'\left(\sum^{N_{i}}_{l=1}V_{i,l}\times W_{i,l,k} +B_{i+1,k}\right)\times W_{i,j,k} k=1∑Ni+1∂Vi+1,k∂L×f′(l=1∑NiVi,l×Wi,l,k+Bi+1,k)×∂Vi,j∂Vi,j×Wi,j,k=k=1∑Ni+1∂Vi+1,k∂L×f′(l=1∑NiVi,l×Wi,l,k+Bi+1,k)×Wi,j,k
把 ∑ l = 1 N i V i , l × W i , l , k + B i + 1 , k \sum^{N_{i}}_{l=1}V_{i,l}\times W_{i,l,k} +B_{i+1,k} ∑l=1NiVi,l×Wi,l,k+Bi+1,k 换成 R i + 1 , k R_{i+1,k} Ri+1,k,于是原式等于:
∑ k = 1 N i + 1 ∂ L ∂ V i + 1 , k × f ′ ( R i + 1 , k ) × W i , j , k \sum_{k=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,k}}\times f'\left(R_{i+1,k}\right)\times W_{i,j,k} k=1∑Ni+1∂Vi+1,k∂L×f′(Ri+1,k)×Wi,j,k
再把 ∂ L ∂ V i + 1 , k × f ′ ( R i + 1 , k ) \frac{\partial L}{\partial V_{i+1,k}}\times f'\left(R_{i+1,k}\right) ∂Vi+1,k∂L×f′(Ri+1,k) 记作 d i + 1 , k d_{i+1,k} di+1,k
∑ k = 1 N i + 1 d i + 1 , k × W i , j , k \sum_{k=1}^{N_{i+1}} d_{i+1,k}\times W_{i,j,k} k=1∑Ni+1di+1,k×Wi,j,k
现在损失函数对每一个神经元权值的偏导都可以通过公式求出,下面推导损失函数对权重和偏置的偏导。
根据链式法则:
∂ L ∂ W i , j , k = ∑ l = 1 N i + 1 ∂ L ∂ V i + 1 , l × ∂ V i + 1 , l ∂ W i , j , k \frac{\partial L}{\partial W_{i,j,k}}=\sum_{l=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,l}}\times \frac{\partial V_{i+1,l}}{\partial W_{i,j,k}} ∂Wi,j,k∂L=l=1∑Ni+1∂Vi+1,l∂L×∂Wi,j,k∂Vi+1,l
将正向传播公式代入,在求和中只保留不为 0 0 0 的项可得:
∑ l = 1 N i + 1 ∂ L ∂ V i + 1 , l × ∂ V i + 1 , l ∂ W i , j , k = ∂ L ∂ V i + 1 , k × f ′ ( R i + 1 , k ) × ∂ V i , j × W i , j , k ∂ W i , j , k = ∂ L ∂ V i + 1 , k × f ′ ( R i + 1 , k ) × V i , j = d i + 1 , k × V i , j \sum_{l=1}^{N_{i+1}}\frac{\partial L}{\partial V_{i+1,l}}\times \frac{\partial V_{i+1,l}}{\partial W_{i,j,k}}\\ =\frac{\partial L}{\partial V_{i+1,k}}\times f'\left(R_{i+1,k}\right)\times\frac{\partial V_{i,j}\times W_{i,j,k}}{\partial W_{i,j,k}}\\ =\frac{\partial L}{\partial V_{i+1,k}}\times f'\left(R_{i+1,k}\right)\times V_{i,j}\\ =d_{i+1,k}\times V_{i,j} l=1∑Ni+1∂Vi+1,l∂L×∂Wi,j,k∂Vi+1,l=∂Vi+1,k∂L×f′(Ri+1,k)×∂Wi,j,k∂Vi,j×Wi,j,k=∂Vi+1,k∂L×f′(Ri+1,k)×Vi,j=di+1,k×Vi,j
偏置的偏导:
∂ L ∂ B i , j = ∂ L ∂ V i , j × ∂ V i , j ∂ B i , j = ∂ L ∂ V i , j × f ′ ( R i , j ) × ∂ ∑ k = 1 N i − 1 W i − 1 , k , j × V i − 1 , k + B i , j ∂ B i , j = ∂ L ∂ V i , j × f ′ ( R i , j ) × 1 = ∂ L ∂ V i , j × f ′ ( R i , j ) = d i , j \frac{\partial L}{\partial B_{i,j}}=\frac{\partial L}{\partial V_{i,j}}\times \frac{\partial V_{i,j}}{\partial B_{i,j}}\\ =\frac{\partial L}{\partial V_{i,j}}\times f'(R_{i,j})\times \frac{\partial \sum_{k=1}^{N_{i-1}}W_{i-1,k,j}\times V_{i-1,k}+B_{i,j}}{\partial B_{i,j}}\\ =\frac{\partial L}{\partial V_{i,j}}\times f'(R_{i,j})\times1\\ =\frac{\partial L}{\partial V_{i,j}}\times f'(R_{i,j})\\ =d_{i,j} ∂Bi,j∂L=∂Vi,j∂L×∂Bi,j∂Vi,j=∂Vi,j∂L×f′(Ri,j)×∂Bi,j∂∑k=1Ni−1Wi−1,k,j×Vi−1,k+Bi,j=∂Vi,j∂L×f′(Ri,j)×1=∂Vi,j∂L×f′(Ri,j)=di,j
通过公式可以看到,第 i i i 层参数的梯度依赖第 i + 1 i+1 i+1 层参数的梯度,所以更新时是从最后一层往前反向更新的。这就是误差从后往前传播。
代码实现
代码照着上面公式打就行,不难。蒟蒻不会 python 只能用 c++ 了。
#include<bits/stdc++.h>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
using namespace std;
const int M=3,N[M+1]={0,2,5,1},MAXN=5;
const long double eta=0.01;//层数,每一层神经元数,每层神经元数的最大值,学习率
long double W[M+5][MAXN+5][MAXN+5],B[M+5][MAXN+5];//权重,偏置
long double V[M+5][MAXN+5],R[M+5][MAXN+5],o[MAXN+5];//神经元输出值,神经元接收值,输出层预期值
long double pV[M+5][MAXN+5],d[M+5][MAXN+5];//对权值的偏导
long double ReLU(long double x){return (x>0?x:0);}
long double pReLU(long double x){return (x>0?1:0);}
void FP()//forward propagation正向传播
{
memset(R,0,sizeof R);
for(int i=2;i<=M;i++)
for(int j=1;j<=N[i];j++)
{
for(int k=1;k<=N[i-1];k++)R[i][j]+=V[i-1][k]*W[i-1][k][j];
R[i][j]+=B[i][j];
V[i][j]=ReLU(R[i][j]);
}
}
long double BP()//Back Propagation反向传播,返回值是误差
{
memset(pV,0,sizeof pV);
for(int i=1;i<=N[M];i++)pV[M][i]=V[M][i]-o[i],d[M][i]=pV[M][i]*pReLU(R[M][i]);
for(int i=M-1;i>=2;i--)
for(int j=1;j<=N[i];j++)
{
for(int k=1;k<=N[i+1];k++)
pV[i][j]+=d[i+1][k]*W[i][j][k];
d[i][j]=pV[i][j]*pReLU(R[i][j]);
}
for(int i=M-1;i>=1;i--)
for(int j=1;j<=N[i];j++)
for(int k=1;k<=N[i+1];k++)
W[i][j][k]-=eta*d[i+1][k]*V[i][j];
for(int i=M;i>=2;i--)
for(int j=1;j<=N[i];j++)
B[i][j]-=eta*d[i][j];
long double L=0;
for(int i=1;i<=N[M];i++)L+=(V[M][i]-o[i])*(V[M][i]-o[i]);
return L*0.5;
}
void gettest()
{
//在这里对输入层和预期值进行赋值,输入值尽量在[-1,1],如果超过可以除以一个大数
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
mt19937_64 e(time(0));
uniform_real_distribution<long double> u(-1,1);
for(int i=1;i<=M-1;i++)
for(int j=1;j<=N[i];j++)
for(int k=1;k<=N[i+1];k++)
W[i][j][k]=u(e);
for(int i=1;i<=M;i++)
for(int j=1;j<=N[i];j++)
B[i][j]=u(e);//初始化参数
int T=10000000;//训练次数
for(int i=1;i<=T;i++)
{
gettest();
FP();
long double loss=BP();
if(i%100000==0)cout<<loss<<endl;//每隔100000组数据输出一次误差
}
return 0;
}
- 回归问题:直接将输入值和需要预测的值输入即可。
- 多标签分类问题(可同时为一个标签):输入需要分类的数据,输出每一种类别的概率,此时输出层激活函数应该为 Sigmoid 等输出值在 ( 0 , 1 ) (0,1) (0,1) 的激活函数。
- 多元互斥分类问题(不可同时为一个标签):输出层激活函数应该为 Softmax 等输出值在 ( 0 , 1 ) (0,1) (0,1) 且输出值之和等于 1 1 1 的激活函数。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号