[AGC005]:F - Many Easy Problem

F - Many Easy Problems

---

Time limit : 5sec / Memory limit : 512MB

Score : 1900 points

Problem Statement

One day, Takahashi was given the following problem from Aoki:

• You are given a tree with N vertices and an integer K. The vertices are numbered 1 through N. The edges are represented by pairs of integers (a_i,b_i).
• For a set S of vertices in the tree, let f(S) be the minimum number of the vertices in a subtree of the given tree that contains all vertices in S.
• There are 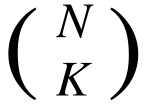ways to choose K vertices from the trees. For each of them, let S be the set of the chosen vertices, and find the sum of f(S) over all 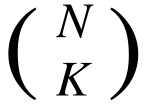ways.
• Since the answer may be extremely large, print it modulo 924844033(prime).

Since it was too easy for him, he decided to solve this problem for all K=1,2,…,N.

Constraints

• 2≦N≦200,000
• 1≦a_i,b_i≦N
• The given graph is a tree.

---

Input

The input is given from Standard Input in the following format:

N
a1 b1
a2 b2
:
aN−1 bN−1

Output

Print N lines. The i-th line should contain the answer to the problem where K=i, modulo 924844033.

 

大意：从一棵树中选择$k$个点，记$f(S)$为最小的包括点集$S$的联通子图，求每个$k$的$\sum F(S)$。

思路{

　　直接做比较麻烦。考虑计算点的贡献。

　　一个点$u$被算入联通子图当且仅当选出的$k$个点没有全部在它的子树内或者是子树外。

　　那么用总数减去不合法方案数贡献就是$C_n^k-\sum_{i=1}^{k}C_{a_i}^k$

　　（其中$a_i$为删除$u$后各个连通块的大小。

　　对于$k$来说把这些项单独提出来，在每一个组合数的前面都会有一个系数$p_i$
　　则$Ans_k=\sum_{i=k}^np_i*C_i^k=\dfrac{1}{k!}*\sum_{i=k}^{n}\dfrac{p_i*i!}{(i-k)!}$

　　把记录$p_i*i!$的数组设为$A$，记录$\dfrac{1}{(i-k)!}$数组翻转设为$B$；

　　不难发现变成了一个卷积的形式，由于还要取模，直接上$NTT$做多项式乘法就好了。

}

#include<bits/stdc++.h>
#define LL long long
#define RG register
#define il inline
#define N 400010
#define mod 924844033
using namespace std;
struct ed{int nxt,to;}e[N*2];
int head[N],tot,n,m,R[N*2],A[N*2],B[N*2],fac[N*2],_fac[N*2],sz[N];
void link(int u,int v){e[tot].nxt=head[u];e[tot].to=v;head[u]=tot++;}
void lnk(int u,int v){link(u,v),link(v,u);}
void dfs(int u,int faa){
  A[n]++;
  sz[u]=1;
  for(int i=head[u];i!=-1;i=e[i].nxt){
    int v=e[i].to;if(v==faa)continue;
    dfs(v,u);sz[u]+=sz[v];
    A[sz[v]]--;if(A[sz[v]]<0)A[sz[v]]+=mod;
  }
  A[n-sz[u]]--;if(A[n-sz[u]]<0)A[n-sz[u]]+=mod;  
}
int qp(int a,int b){
  if(!b)return 1;if(a==1)return a;
  int temp=qp(a,(b>>1));
  temp=1ll*temp*temp%mod;
  if(b&1)temp=1ll*temp*a%mod;
  return temp;
}
void NTT(int *a,int f){
  for(int i=0;i<n;++i)if(i<R[i])swap(a[i],a[R[i]]);
  for(int i=1;i<n;i<<=1){
    int gn=qp(5,(mod-1)/(i<<1));
    for(int j=0;j<n;j+=(i<<1)){
      int g=1;
      for(int k=0;k<i;++k,g=1ll*g*gn%mod){
	int x=a[j+k],y=1ll*g*a[j+k+i]%mod;
	a[j+k]=(x+y)%mod;
	a[j+k+i]=(x-y+mod)%mod;
      }
    }
  }
  if(f==-1){
    reverse(a+1,a+n);
    int _n=qp(n,mod-2);
    for(int i=0;i<n;++i)a[i]=1ll*a[i]*_n%mod;
  }
}
int main(){
  memset(head,-1,sizeof(head));
  scanf("%d",&n);for(int i=1;i<n;++i){int u,v;scanf("%d%d",&u,&v),lnk(u,v);}
  dfs(1,1);
  fac[1]=1;fac[0]=1;
  for(int i=2;i<=n;++i)fac[i]=1ll*fac[i-1]*i%mod,A[i]=1ll*A[i]*fac[i]%mod;
  _fac[n]=qp(fac[n],mod-2);for(int i=n;i;--i)_fac[i-1]=1ll*_fac[i]*i%mod;
  for(int i=1;i<=n;++i)B[i]=_fac[n-i];
  m=n;int L=0;
  for(n=1;n<=(m<<1);n<<=1)L++;
  for(int i=0;i<n;++i)R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));
  NTT(A,1),NTT(B,1);
  for(int i=0;i<n;++i)A[i]=1ll*A[i]*B[i]%mod;
  NTT(A,-1);
  for(int i=1;i<=m;++i)printf("%d\n",1ll*A[m+i]*_fac[i]%mod);
  return 0;
}