Efficient Knowledge Graph Accuracy Evaluation 论文笔记
前言
这篇论文主要讲的是知识图谱正确率的评估,将知识图谱的正确率定义为知识图谱中三元组表述正确的比例。如果要计算知识图谱的正确率,可以用人力一一标注是否正确,计算比例。但是实际上,知识图谱往往很大,不可能耗费这么多的人力去标注,所以一般使用抽样检测的方法。这就好像调查一批商品合格率一样,不可能将所有的商品都检查一遍,采用抽样的方法可以估计出合格率。
抽样产生的样本,我们利用中心极限定理,可以推导出样本均值服从正态分布。根据正态分布的概率形式,可以推导置信区间,并且可以要求误差界限(margin of error)在一定范围内。
这篇博客,先给出每种抽样方法的思路。之后按照如下思路分析:置信区间的推导,时间消耗模型(cost),最优化问题,每种抽样方法的置信区间(分析无偏性和 cost)。
抽样检测的思路
1. Simple Random Sampling
随机从知识图谱中抽取 n 个三元组。
2. Cluster Sampling
motivation:标注员在标注三元组的时候,如果元组来自同一个实体,效率会高。理由是,只需了解一个对象,就可以标注多个三元组。
从 N 个实体中,等概率随机抽取 n 个实体,这些实体对应的所有三元组进行判断。
3. Weighted Cluster Sampling
从 N 个实体中,加权随机抽取 n 个实体,这些实体对应的所有三元组进行判断。
4. Two-Stage Weighted Cluster Sampling
Motivation:随机抽取的实体,存在一些实体有着很多的三元组,如果这些元组全部都要判断的话,时间消耗非常多
第一阶段:从 N 个实体中,加权随机抽取 n 个实体
第二阶段:从 n 个实体的三元组中随机抽样,最多抽取 m 个。(后面的实验结果建议 m 取 3~5)
5. Stratified Two-Stage Weighted Cluster Sampling
Motivation:实体的三元组所含有的数量越多,实体的正确率越高,方差越低。
按照实体的数量分层,然后使用两阶段抽样。
在实验中,按照正确率分层,目的是为了给出分层抽样所能达到的一个下界。
evolving KG 抽样检测的思路
evolving KG 表示正在不断更新的知识图谱,我们知道了原知识图谱的正确率,现在加入了新的三元组,我们需要确定加入新三元组之后,知识图谱的正确率。
1. 加权蓄水池算法(WRS)
WRS 中将更新 \(\Delta\) 中的每一个实体视为一个新实体,不管这个实体是否已经存在于原来的知识图谱中。权重为一个实体的三元组个数,而不是占比。
论文中没有讲该如何计算正确率。WRS 每一格对应一个正确率,对于没有被替换的样本,我们可以使用原来计算得出的正确率。对于新加入的样本,我们可以采用简单随机抽样,因为可能某一个更新,它可能包含某一个实体超过上百个三元组,这就非常耗时了。
2. 分层增量评估
新的知识图谱记为\(G + \Delta\),将原知识图谱 \(G\) 和更新 \(\Delta\) 当成分层抽样中的不同层,之后用加权求和。
置信区间
我们需要的是知识图谱的正确率,所以这里推导的是正确率的置信区间。
设正确率的估计量为\(\hat{\mu}\),需要满足无偏性。有了无偏性,我们可以由大数定律得到,正确率的估计量就有越高的概率接近期望值,也就是真实的正确率。
接着,我们给估计量采样,得到 n 个独立同分布的样本\(X_1, X_2, ..., X_n\)。不管这些样本服从什么分布,根据中心极限定理,在样本量充分大的情况下,样本均值近似服从正态分布。
使用概率形式表示置信区间:
因此我们可以说平均值 \(1-\alpha\) 的置信区间是:
后面在使用这个置信区间的时候,我们可以将样本方差代入总体方差。
当然也可以自己算出方差,重新构造置信区间,比如在两阶段抽样中的那样。
时间消耗模型
在评估一个知识图谱正确率的时候,我们需要两个步骤。
- 确定实体。这个实体指的是谁,比如下表中 Task 1 的 MJ 是科学家,而 Task 2 中的 MJ 是运动员。
- 确定表述。确定三元组表述的事实是否正确。
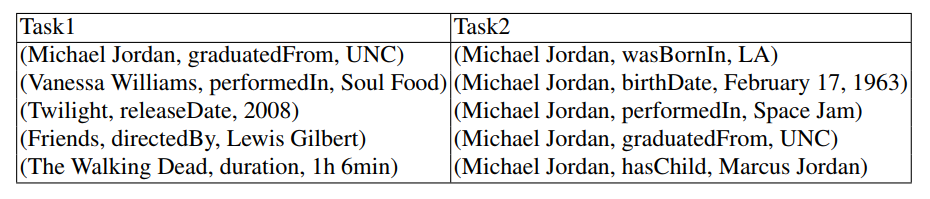
我们发现有如下规律:
- 不同实体越多,我们辨识实体消耗的时间越多。
- 在总数不变的情况下,不同实体越少,实体的三元组越多,总的消耗时间越少,因为我们需要了解一个实体,就可以确定实体相关的三元组。
因此,提出如下 cost function:
\(|E'|\)表示不同实体个数,\(|G'|\)表示抽样产生的知识图谱个数。
\(c_1\)为确定实体消耗,\(c_2\)为确定表述消耗。在后面的实验中,得出了如下数据,\(c_1 = 45, c_2 = 25\)
论文中的公式 2是期望值。随机变量是什么呢?不同的抽样方法!不同抽样方法导致什么不同呢?抽样产生的不同实体个数和抽样总数的不同。我这里就没有写期望了,上面的 cost 函数是已经抽样后的代价。
这个模型有两个作用:
- 最优化的目标
- 模拟实验中,可以拿来估计评估一组三元组需要的时间。我们可以通过合成三元组,再用这个模型计算消耗的时间,实验的时候人力都不需要了。
最优化问题
目标是尽可能减少人力消耗,同时还要满足误差界限在一定范围,并且要求无偏估计。
优化的目标是随着采样数量单调递增的,所以在后面的计算中,都是找采样数量的下界,让采样数量等于下界就是最优化的目标了。
Simple Random Sampling
随机从知识图谱中抽取 \(n_s\) 个三元组。
\(n_s\)个随机变量为:
正确率:
置信区间,二项分布的方差可以用均值表示 \(\hat{\mu_s}(1-\hat{\mu_s})\):
无偏性:
cost 分析:
令 \(n_c\) 表示不同实体的个数,\(n_s\)表示抽取三元组的总数
抽到 \(n_c\) 个不同的实体,我们可以将 \(n_c\) 分解,其中 \(X_i = 0, 1\) 表示“抽\(n_s\)次,第 \(i\) 个实体是否被抽中”的随机变量。
所以 cost 可以写成:
约束条件:
cost 随着 \(n_s\) 增大而增大,所以取下界,即是理论上,最少的采样数量。
你会发现,这个采样数量和知识图谱的总大小无关,和知识图谱的正确率有关!
Random Cluster Sampling
从 N 个实体中,等概率随机抽取 n 个实体,这些实体对应的所有三元组进行判断。
n 个随机变量,\(\tau_{I_k}\)表示第\(I_k\)个实体的正确三元组个数:
正确率:
置信区间:
无偏性:
Weighted Cluster Sampling
从 N 个实体中,加权随机抽取 n 个实体,这些实体对应的所有三元组进行判断。
n 个随机变量,\(\mu_{I_k}\) 表示第 \(I_k\) 个实体的正确率:
正确率:
置信区间:
无偏性:
Two-Stage Weighted Cluster Sampling
第一阶段:从 N 个实体中,加权随机抽取 n 个实体
第二阶段:从 n 个实体的三元组中随机抽样,最多抽取 m 个。(后面的实验结果建议 m 取 3~5)
n 个随机变量,每个随机变量为随机抽样 m 个得到的正确率:
正确率:
置信区间:
无偏性:
cost 分析:
这里论文中算出了 \(\hat\mu_{w, m}\) 的方差为 \(Var(\hat\mu_{w, m})\),因此我们可以使用中心极限定理构造新的关于 \(Var(\hat\mu_{w, m})\)置信区间:
重新构造置信区间
约束:
所以我们才有公式 11 下面的那个表达式(我在这里卡了半天,一直在盲目代公式算,最终才意识到应该重新构造置信区间)
Stratified Two-Stage Weighted Cluster Sampling
分层随机抽样,按照实体所含有的三元组个数分层。在计算准确率的时候,加权计算每层准确率大小。
因为按照个数分层,每一层可以得到更小的方差,所以分层抽样的方差要小于不分层抽样的方差。因此,结合误差界限来看,当方差越小,需要判断抽样的数量越少,所以分层需要耗费的标注时间更少。
Reservoir Incremental Evaluation
这一小节没有讲清楚,WRS 得到的结果该如何去计算正确率。
WRS 中的加权,权重是一个实体的三元组个数 \(M_i\)。一开始一直在纠结用比例 \(M_i / M\),一直没搞懂如何才能保持比例不变呢。 WRS 中将 \(\Delta\) 中的每一个实体视为一个新实体,不管这个实体是否已经存在于原来的知识图谱中。
WRS 的结果为按权重抽样的结果,计算正确率的时候使用 WCS 的公式即可。当然,某个更新可能包含一个实体的几百个三元组,此时可以对这个样本进行简单随机抽样,计算正确率,再用 TWCS 的公式来计算。

Stratified Incremental Evaluation
新的知识图谱记为\(G + \Delta\),将原知识图谱 \(G\) 和更新 \(\Delta\) 当成分层抽样中的不同层,之后用加权求和。

对于多组更新,可以将每一次更新都当成分层抽样的一层,之后再加权求和计算准确率。
实验中重要的结论
实验也是非常重要的部分,这里可以让你直观的了解到每种方法的优点和缺点,了解一些重要参数和方法。
比如,TWCS 评估的时间不受知识图谱的大小影响!!这一结论真是太震惊了。
cost function
时间消耗模型中的参数为 \(c_1 = 45, c_2 = 25\)
Oracle Stratification
按照实际的正确率来分层,方差可以大大减少。从而我们可以确定分层之后,可以达到的最优解。这种分层方法仅仅是理想的分层,实际上我们并不能知道知识图谱的结构,我们用这种方法来确定分层能达到的最优解。
static KG evaluation
所有方法中,TWCS 效率最高。
TWCS 对比 SRS,TWCS 抽取的实体种类少,TWCS 相比 SRS 大概节约 20% 的时间。但是,在高准确率的情况下,TWCS 又是并不明显,有的甚至比 SRS 慢。
TWCS 中 m 的数值
一般来说,评估的时间先随着 m 的增大而减小,到了最低点后,又随着 m 的增大而增大。因为 m 大于一定值的时候,再增大 m 并不能减少需要抽取的实体个数 n。
理论上,m 的数值取决于实体大小和准确率的分布;实践上,m 推荐设置为 3~5。
分层采样
我们预设了“实体的三元组数量越多,正确率越高”,根据这一假设合成了 MOVIE-SYN,然后在上面的实验结果非常美丽动人。
但是,在真实的知识图谱上进行的时候,发现并不奏效。
结论:
in practice, cluster size may serve as a good signal indicating similarities among entity accuracies for large clusters but not for those small ones, and the overall variance is not reduced as we expected.
TWCS 评估时间的影响因素
TWCS 评估的时间不受知识图谱的大小影响!!!
TWCS 评估的时间受到知识图谱正确率的影响,在 50% 正确率的情况下,达到最大。
Single Batch of Update
不管更新内容的大小还是更新内容的准确率,SS 都比 RS 好。
Sequence of Updates
RS 能够 fault-tolerant。实验结果表明,如果一开始知识图谱的正确率评估是不准确的,那么再接下来的更新中,RS 能够较快的进入实际的正确率,但是 SS 一直受到之前结果的影响,很难达到实际的正确率。
因此,在需要多次、少量更新知识图谱的情况下,推荐使用 RS。
Q&A
1,每个抽样方法的 cost 分析得出的抽样数量究竟有什么用?比如,SRS 中我们抽样了 \(n_s\) 个,得到了均值,再用这个均值反推 \(n_s\),这不就死锁了吗?再比如,TWCS 中我们需要知道知识图谱每个实体的准确率,整体的正确率,我们才能求 \(n, m\),我们去优化这个问题干什么呢?
实际上,我们采样的时候,采样的数量我们可以自己决定。
在 SRS 中,根据第 4 节的整体框架,我们每次抽取 a small batch of samples(每次我们抽 30 个),放入已经判断过的样本一起,然后让人判断新加入的样本是否正确。判断结束之后,使用全部样本计算均值。再用这个均值计算是否达到最少需要的样本,如果达到了,那么可以停止了,如果没有,那么还要继续。所以,n_s 的下界给出来的作用是,简化 Quailty Control 的判断。并不是我认为的,需要抽取的数量。
在 TWCS 中,m 取决于知识图谱的结构,但是我们事先根本不知道知识图谱的结构是如何的,根本无法计算 m。所以通过做实验,推荐 m 为 3~5。那么判断是否结束的条件,可以看看样本来是否达到了 nm 个,如果达到了,就可以结束采样了。
另外,我们分析的目的是,确定最优的抽样算法,而不是确定需要采样的数量是多少!比如,在对比 “TWCS” 和“分层的TWCS”两种方法的时候,分析出了方差更小,误差界限的不等式可以推出分层需要的样本量更小,代价更小。所以,代价分析的结果是,分层的 TWCS 更好,当然了,实验结果表明并不,因为分层的方式出发点不对。
2,RCS 和 WCS 的 cost 如何分析?
不分析!
这里不分析 RCS 和 WCS,原因很简单,因为这两种方法在随机抽取 n 个实体之后,把这个实体的所有三元组都拿出来判断了,但是有时候一个实体的三元组很多,这样就消耗了更多时间了。从实验来看,确实存在这种情况。
实际上,这两者的 cost 取决于知识图谱的结构,可能抽取到某些实体的三元组个数特别多,因此消耗更多的时间。
3,为什么 TWCS 需要计算出方差,而不用样本方差呢?
假如我们直接拿样本来分析,我们有 \(n\) 个不同的实体,一共抽取了 \(\sum^n_{k=1} min\{M_{I_k}, m\}\) 个实体。
优化目标是:
这里 \(n\) 和 \(\sum^n_{k=1} min\{M_{I_k}, m\}\) 都是优化目标的变量,但是\(\sum^n_{k=1} min\{M_{I_k}, m\}\)不好搞。
所以,在 TWCS 中,我们分析 cost,先分析正确率的方差(就是那个比较复杂的公式),然后重新构造置信区间,再分析 cost。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号