第四章 线性回归

Recall:

最简单的回归模型是输入变量的线性组合：

\[y(\mathbf{x}, \mathbf{w}) = w_0 + w_1 x_1 + \cdots + w_D x_D \]

其中：

• \(\mathbf{x} = (x_1, \cdots, x_D)^\top\) 是输入向量；
• \(\mathbf{w} = (w_0, w_1, \cdots, w_D)\) 是权重参数；
• \(y(\mathbf{x}, \mathbf{w})\) 是模型对输入 \(\mathbf{x}\) 的预测输出。

“线性回归”（linear regression）有时专指这种形式。
模型不仅对参数 \(w_0, \cdots, w_D\) 是线性的（即没有平方或乘积等非线性变换），它对输入变量 \(x_i\) 也是线性的。这种特性给模型带来限制。

基函数

为了突破这种限制，我们通过输入变量的固定非线性函数的线性组合来扩展之前的模型：

\[y(\mathbf{x}, \mathbf{w}) = \sum_{j=0}^{M-1} w_j \phi_j(\mathbf{x}) \]

其中：

• \(\phi_j(\mathbf{x})\) 是基函数；
• \(w_j\) 是对应的权重参数；
• \(\phi_0(\mathbf{x}) = 1\) 是常数项，用于表示偏置 \(w_0\)。

\[y(\mathbf{x}, \mathbf{w}) = \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}) \]

• 其中 \(\mathbf{w} = (w_0, ..., w_{M-1})^T\)，
  \(\boldsymbol{\phi}(\mathbf{x}) = (\phi_0(\mathbf{x}), ..., \phi_{M-1}(\mathbf{x}))^T\)

NOTE: 虽然 \(\phi_j(\mathbf{x})\) 可能是非线性的，但模型整体仍被称为线性模型，因为它对参数 \(\mathbf{w}\) 是线性的。

基函数的其他形式

1. 多项式基函数：

   \[\phi_j(x) = x^j \]
   • 用于多项式回归。

2. 高斯基函数 ：

   \[\phi_j(x) = \exp\left( - \frac{(x - \mu_j)^2}{2s^2} \right) \]
   • \(\mu_j\)：控制中心位置；
   • \(s\)：控制宽度（尺度）。

3. Sigmoid 基函数：

   \[\phi_j(x) = \sigma\left( \frac{x - \mu_j}{s} \right) \]

   • \(\sigma(a)\)：Sigmoid 函数，定义为：

     \[\sigma(a) = \frac{1}{1 + \exp(-a)} \]

   • 可替代为 tanh：\(\tanh(a) = 2\sigma(2a) - 1\)

4. 傅里叶基函数（Fourier Basis）：

   • 使用正弦波展开，适合表示周期性和频域特征。

5. 小波基函数（Wavelet Basis）：

   • 适用于时频局部化分析；
   • 在图像和时间序列处理中特别有用；
   • 通常具有正交性，适合规则网格输入。

似然函数

\[\ln p(\mathbf{t} | \mathbf{X}, \mathbf{w}, \sigma^2) = \sum_{n=1}^N \ln \mathcal{N}(t_n \mid \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n), \sigma^2) \]

单个高斯分布的概率密度函数形式：

\[\mathcal{N}(t_n \mid \mu_n, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( - \frac{(t_n - \mu_n)^2}{2\sigma^2} \right) \]

在我们的回归模型中：

• \(\mu_n = \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n)\)

所以代入进去：

\[\mathcal{N}(t_n \mid \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n), \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( - \frac{(t_n - \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n))^2}{2\sigma^2} \right) \]

对这个式子取对数：

\[\ln \mathcal{N}(t_n \mid \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n), \sigma^2) = -\frac{1}{2} \ln(2\pi \sigma^2) - \frac{(t_n - \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n))^2}{2\sigma^2} \]

所以总的对数似然为：

\[\ln p(\mathbf{t} | \mathbf{X}, \mathbf{w}, \sigma^2) = \sum_{n=1}^N \left[ -\frac{1}{2} \ln(2\pi \sigma^2) - \frac{(t_n - \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n))^2}{2\sigma^2} \right] \]

\[= -\frac{N}{2} \ln(2\pi \sigma^2) - \frac{1}{2\sigma^2} \sum_{n=1}^N (t_n - \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n))^2 \]

拆开再写清楚：

\[= -\frac{N}{2} \ln(2\pi) - \frac{N}{2} \ln(\sigma^2) - \frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{n=1}^N (t_n - \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n))^2 \]

最后一项定义为 \(E_D(\mathbf{w})\)：

\[E_D(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^N (t_n - \mathbf{w}^T \boldsymbol{\phi}(\mathbf{x}_n))^2 \]

所以最终得出：

\[\ln p(\mathbf{t} | \mathbf{X}, \mathbf{w}, \sigma^2) = -\frac{N}{2} \ln \sigma^2 - \frac{N}{2} \ln(2\pi) - \frac{1}{\sigma^2} E_D(\mathbf{w}) \]

• \(E_D(\mathbf{w})\) 来自对数高斯分布中的平方项；
• 它其实就是我们熟悉的平方损失函数（loss function）；
• 最大化似然函数 ⟺ 最小化 \(E_D(\mathbf{w})\)。

最大似然

写出似然函数后，我们可以通过最大似然来确定w和σ2。

\(\mathbf{w}\)

在给定输入 \(x_n\) 和输出 \(t_n\) 的条件下，假设数据服从高斯分布，似然函数关于 \(\mathbf{w}\) 的对数梯度为：

\[\nabla_{\mathbf{w}} \ln p(\mathbf{t} \mid \mathbf{X}, \mathbf{w}, \sigma^2) = \frac{1}{\sigma^2} \sum_{n=1}^N (t_n - \mathbf{w}^T \boldsymbol{\phi}(x_n)) \boldsymbol{\phi}(x_n)^T \tag{4.12} \]

将梯度设为零，得出极值条件：

\[0 = \sum_{n=1}^N t_n \boldsymbol{\phi}(x_n)^T - \mathbf{w}^T \sum_{n=1}^N \boldsymbol{\phi}(x_n) \boldsymbol{\phi}(x_n)^T \tag{4.13} \]

最优解：正规方程（Normal Equation）

整理后得出最大似然估计：

\[\mathbf{w}_{ML} = (\boldsymbol{\Phi}^T \boldsymbol{\Phi})^{-1} \boldsymbol{\Phi}^T \mathbf{t} \tag{4.14} \]

这里：

• \(\boldsymbol{\Phi}\)：设计矩阵，行是输入样本经基函数变换后的向量；
• \(\mathbf{t}\)：目标向量（标签）；

设计矩阵

设计矩阵 \(\boldsymbol{\Phi}\) 的定义：

\[\boldsymbol{\Phi} = \begin{bmatrix} \phi_0(x_1) & \phi_1(x_1) & \cdots & \phi_{M-1}(x_1) \\ \phi_0(x_2) & \phi_1(x_2) & \cdots & \phi_{M-1}(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(x_N) & \phi_1(x_N) & \cdots & \phi_{M-1}(x_N) \end{bmatrix} \]

伪逆定义为：

\[\boldsymbol{\Phi}^{\dagger} \equiv (\boldsymbol{\Phi}^T \boldsymbol{\Phi})^{-1} \boldsymbol{\Phi}^T \]

这是 Moore-Penrose 伪逆，适用于 \(\boldsymbol{\Phi}\) 不满秩时的广义解。

\(w_0\)

如果将偏置项 \(w_0\) 单独处理，可以重新写误差函数为：

\[E_D(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^N \left\{ t_n - w_0 - \sum_{j=1}^{M-1} w_j \phi_j(x_n) \right\}^2 \]

对 \(w_0\) 求导得最小值点：

\[w_0 = \bar{t} - \sum_{j=1}^{M-1} w_j \bar{\phi}_j \]

其中：

• \(\bar{t}\)：样本目标值均值
• \(\bar{\phi}_j\)：第 \(j\) 个基函数在所有样本上的均值

\(\sigma^2\)

我们把对数似然函数对 \(\sigma^2\) 求导，并令导数为 0，可以推导得到：

\[\sigma^2_{ML} = \frac{1}{N} \sum_{n=1}^N \left( t_n - \mathbf{w}_{ML}^T \phi(x_n) \right)^2 \tag{4.20} \]

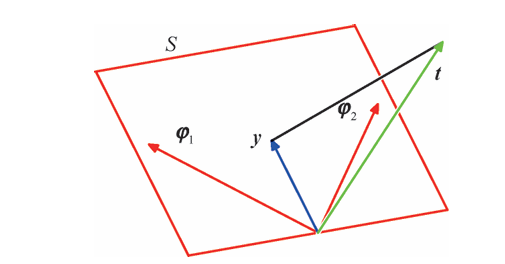
最小二乘的几何表示

序贯学习

序贯学习又称在线算法，适用于：

1. 数据集非常大，使用序贯可以一个一个数据点的对参数进行更新
2. 实时应用场景，数据连续的流式到达们需要在所有数据可获得前预测

随机梯度下降又称序贯梯度下降，假设误差函数 \(E\) 为所有数据点误差项 \(E_n\) 的总和：

\[E = \sum_n E_n \]

我们希望通过最小化总误差函数 \(E\) 来优化参数 \(\mathbf{w}\)。

随机梯度下降的基本更新公式为：

\[\mathbf{w}^{(\tau+1)} = \mathbf{w}^{(\tau)} - \eta \nabla E_n \tag{4.21} \]

• \(\tau\)：迭代次数；
• \(\eta\)：学习率（step size）；
• \(E_n\)：对第 \(n\) 个样本的误差项；

正则化最小二乘法

思想：在误差函数中添加正则化项来控制过拟合

多重输出

直觉是可以通过为t（目标向量）的每个分量引入一组不同的基函数，我们得到多个独立的回归问题。然而，更常见的方法是使用相同的一组基函数来对目标向量的所有分量建模。