第一章：深度学习革命

Note:本文是在DataWhale的活动期间撰写，推荐关注相关公众号共同学习。

通过应用引入相关概念

1.医疗诊断场景

训练集：被标注为恶性或良性的病变图像集，标注依据为对病变活检后得到的真实分类。

训练集用处：确定深度神经网络中2500万个可调参数（权重）的取值。

训练目标：训练好的神经网络可以根据新图像预测病变是良性还是恶性，而无需执行耗时的活检。

训练过程：学习参数值的过程称为学习（learning）或训练（training）。属于监督学习（supervised learning） ，属于分类（classification) 任务，因为每个样本都带有正确的类别标签（良性/恶性）。

挑战与解决方案：
带标注的训练图像数量相对较少（仅约12.9万幅），因此研究人员采用迁移学习（transfer learning） 策略：
先在包含128万幅日常物体图像（如狗、建筑和蘑菇等）的大型数据集上预训练深度神经网络，然后在皮肤病变图像数据集上进行微调（fine-tune）。

结果：
使用深度学习技术对皮肤病变图像进行分类的准确率，已经超过专业皮肤科医生的水平（Brinker et al., 2019）

2. 蛋白质结构预测

同属于监督学习，但是输出是结构预测，感兴趣可阅读 AlphaFold算法。

3. 图像合成

训练集：一组无标注的人脸图像，拍摄于摄影棚中、背景单一、清晰度高，提供了丰富的面部特征信息。

训练集用处：用于训练深度神经网络，使其能够捕捉这些图像的潜在分布特征，进而生成具有类似统计特性但并非真实存在的人脸图像。

训练目标：训练后的神经网络能够合成看起来极其逼真的新图像，这些图像从未在训练集中出现，但质量极高，难以与真实照片区分开。

训练过程：此任务不依赖于“图像-标签”对，而是通过无监督学习（unsupervised learning） 方法训练 生成式模型（generative model) 。

变体：能根据输入的文本字符串（称
为提示词，prompt）生成反映文本语义的图像。

我们用生成式AI（generative AI） 这个术语来描述那些能生成图像、视频、音频、文本、候选药物分子或其他形态信息的深度学习模型。

4. 大语言模型

训练集：大型文本数据集，无需人工标注。

训练集用处：以在大型文本数据集上通过提取训练对（training pair）进行训练。练对的输入是随机选定的词序列，输出是已知的下一个词。

训练目标：从输入到输出映射函数，
有标注的输出是从输入训练数据中自动获取的，无须进行另外的人工标注。

训练过程：
采用自监督学习（self-supervised learning） 策略训练自回归语言模型（autoregressive language model）。

应用场景：以一个词序列作为输入，生成这个词序列最可能的下一个词，我们可以把末尾添加了新词的扩展序列再输入到模型中，让它生成后续的词，重复这个过程，就会得到越来越长的词序列。这样的模型还可以输出一个特殊的 “停止” 词，来表示文本生成的结束，这样就使得模型在输出一定长度的文本后停止。此时，用户可以在词序列的末尾添加自定义的词序列，然后将完整的词序列重新输入模型以触发生成后续的词。通过这种方式，人们就可以和神经网络对话了。

教学示例

监督学习问题：用多项式拟合一个小型合成数据集，目标是根据输入的变量值，对目标变量进行预测。

1. 合成数据

输入与目标变量

• 输入变量：\(x \in [0, 1]\)
• 目标变量：\(t \in \mathbb{R}\)

训练集定义

• 输入数据点：\(\{x_n\}_{n=1}^N\)，其中 \(x_n \sim \text{Uniform}(0,1)\)

• 理想目标值（无噪声）：

  \[t_n^{\text{ideal}} = \sin(2\pi x_n) \]

• 加噪声后的目标值：

  \[t_n = \sin(2\pi x_n) + \epsilon_n \]

  其中噪声 \(\epsilon_n \sim \mathcal{N}(0, \sigma^2)\)

Note: 关于高斯分布概率密度函数的粗糙直觉

学习目标

• 学习一个函数 \(y(x) \approx t\)，使得在新的输入 \(x\) 上预测 \(t\) 的值
• 本质上是从观测数据 \(\{x_n, t_n\}_{n=1}^N\) 学习函数 \(y(x) \approx \sin(2\pi x)\)
  

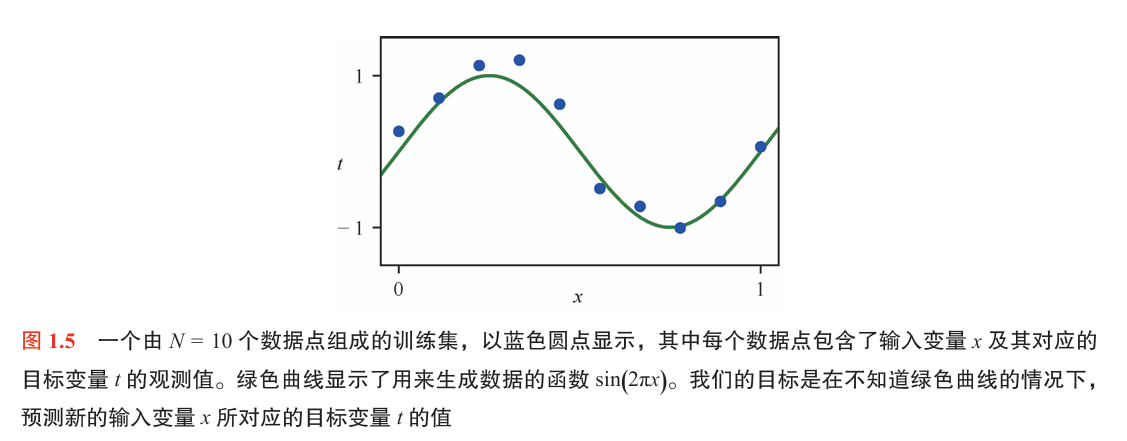
2. 线性模型

我们将使用多项式函数来拟合数据：

\[y(\mathbf{x}, \mathbf{w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M = \sum_{j=0}^M w_j x^j \]

为什么是线性模型？

尽管多项式函数 \(y(x, w)\) 是 \(x\) 的非线性函数，但它是参数 \(w\) 的线性函数。

换句话说，虽然模型关于输入 \(x\) 是非线性的（因为有 \(x^2, x^3, \dots\)），但是关于参数 \(w_j\) 是线性的组合，因此称之为线性模型（linear model）。

这是机器学习中一个重要的分类标准——线性模型是否线性，是指对参数是否线性，而不是对输入。

3. 误差函数

\[E(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^{N} \left\{ y(x_n, \mathbf{w}) - t_n \right\}^2 \]

我们可以通过选择能够使 \(E(\mathbf{w})\) 尽可能小的 \(\mathbf{w}\) 值来解决曲线拟合问题。

训练目标：最小化误差函数

因为平方和误差函数是参数 \(\mathbf{w}\) 的二次函数，其对参数 \(\mathbf{w}\) 的导数是线性函数，所以该误差函数的最小值有且仅有一个唯一解。

这是一种凸优化问题，可以通过解析形式求得封闭解。

4. 模型复杂度

我们还面临选择多项式的阶数M的问题，这将引出模型比较（model comparison）或模型选择（model selection）这一重要概念。下图中的拟合实例分别使用阶数M = 0-9的多项式来拟合数据集：

（感谢组员提供实验结果，等后续完善附上其链接）

模型在训练集上的拟合

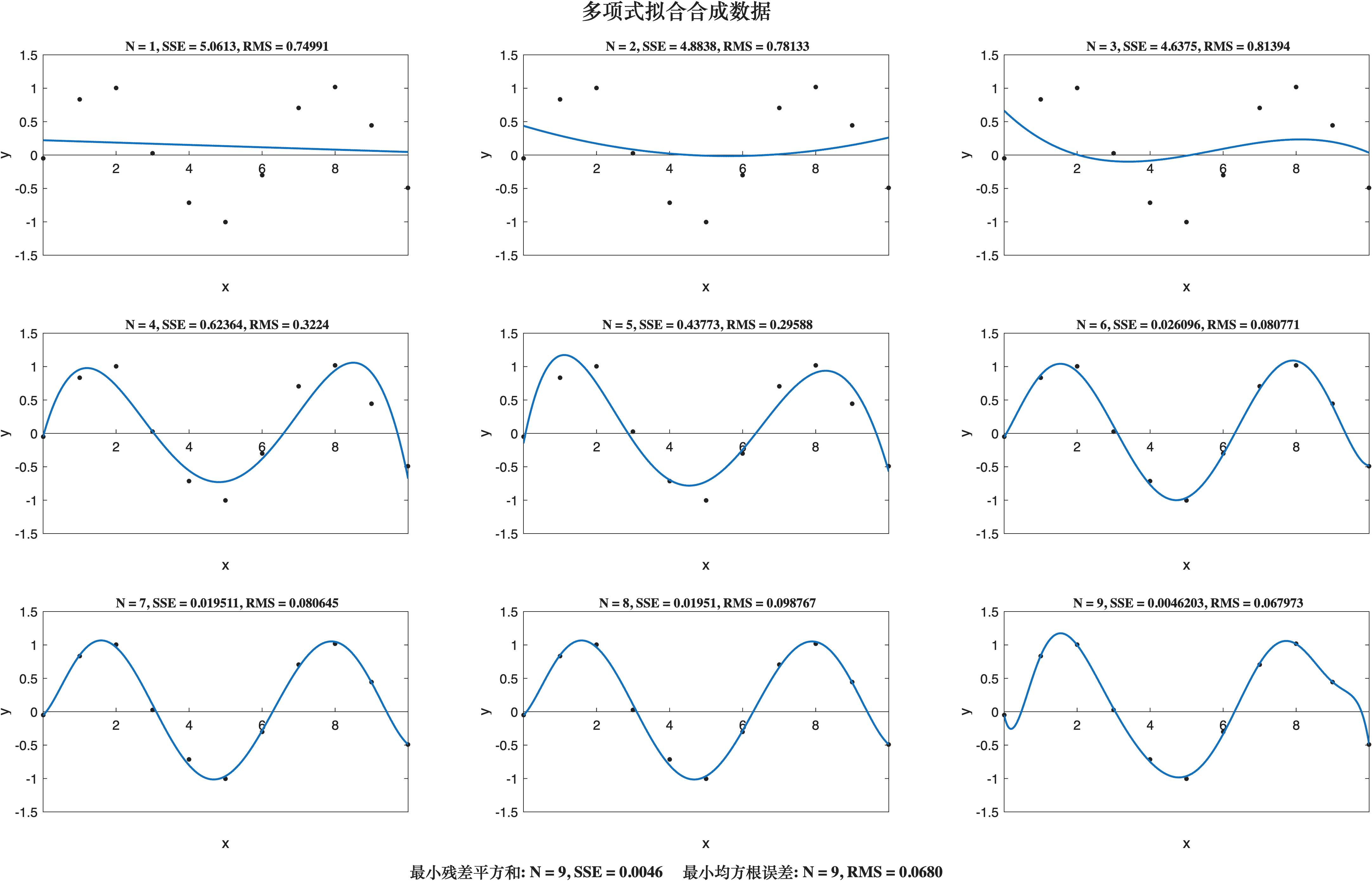
模型在测试集上的表现

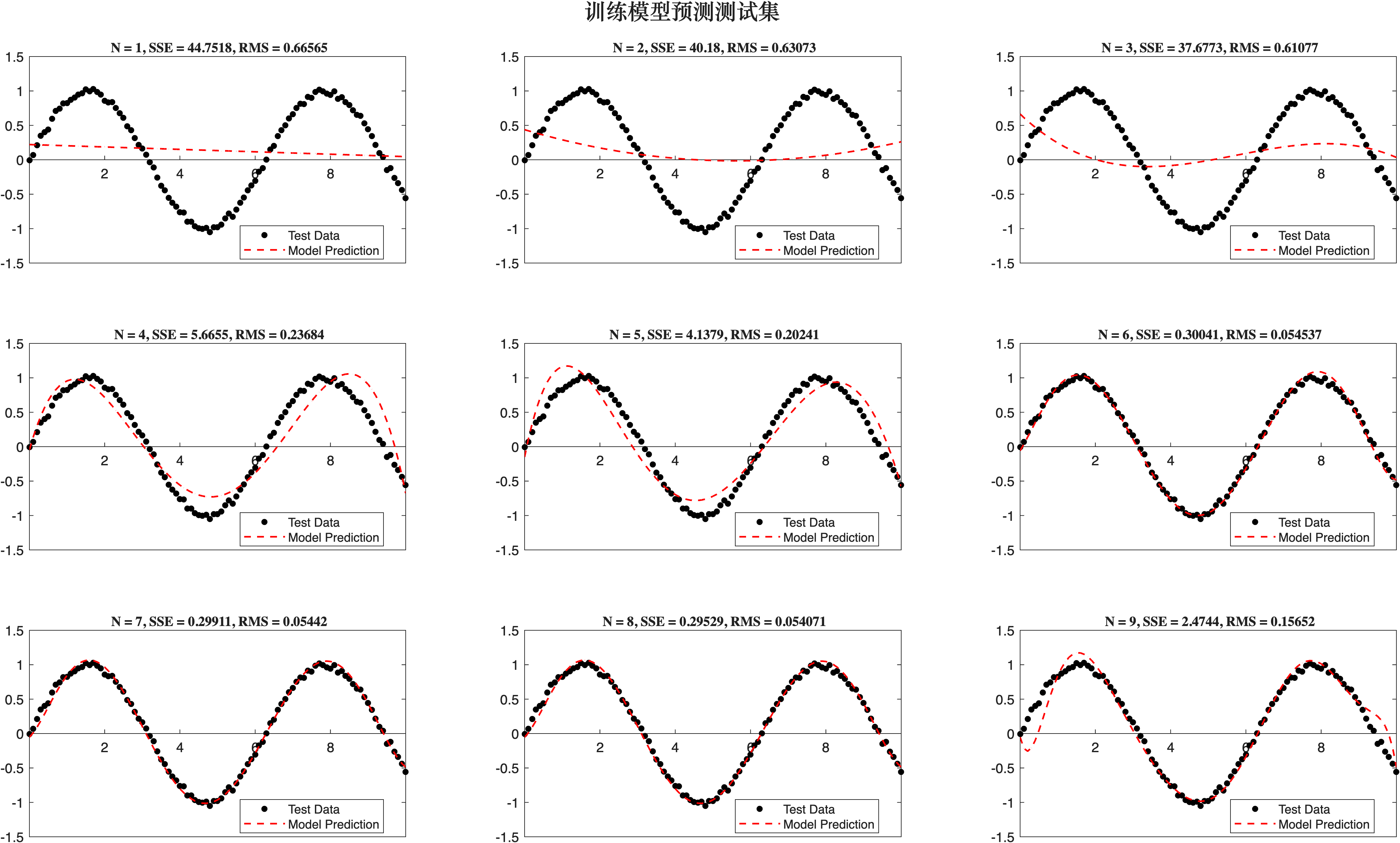
✦ 拟合训练数据：阶数越高，误差越小

• 随着多项式阶数 \(M\) 增加，模型对训练集的拟合误差（例如 SSE、RMS）持续下降。
• 高阶多项式（如 \(M=9\)）甚至可以将训练误差降到接近 0，实现“完美拟合”。
• 但这会出现严重波动，无法反映真实的 \(\sin(2\pi x)\) 函数，属于过拟合（overfitting） 现象。

✦ 泛化到测试集：存在“最优”阶数

• 对独立测试集，RMS 误差先下降再上升，呈现出“U型曲线”：

  • 低阶模型（如 \(M=0\sim2\)）欠拟合，表现差；
  • 高阶模型（如 \(M=9\)）在训练集表现极佳，但测试集误差反而升高，泛化能力差。

✦ 均方根误差公式

用于度量模型预测值与真实值之间的平均偏差，公式如下：

\[E_{\text{RMS}} = \sqrt{\frac{1}{N} \sum_{n=1}^N (y(x_n, \mathbf{w}) - t_n)^2} \]

总的来说，在这一部分我们可以看出，当模型复杂度固定时，数据集越大，过拟合现象就越不明显。换言之，数据量越大，我们就能用越复杂（即更灵活）的模型去拟合数据。
经典统计学中有一条常用的启发式经验：训练数据点的数量应至少是模型中可学习参数数量的若干倍（比如5倍或10倍）。然而，我们在本书继续探讨深度学习后会发现，即使模型参数的数量远远超过训练数据点的数量，也一样可以获得非常出色的结果（双下降现象）。

5. 正则化

\[\tilde{E}(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^{N} \left( y(x_n, \mathbf{w}) - t_n \right)^2 + \frac{\lambda}{2} \| \mathbf{w} \|^2 \]