洛谷刷题（一）

P1007独木桥

题目背景

战争已经进入到紧要时间。你是运输小队长，正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激，于是命令你的士兵们到前方的一座独木桥上欣赏风景，而你留在桥下欣赏士兵们。士兵们十分愤怒，因为这座独木桥十分狭窄，只能容纳

题目描述

突然，你收到从指挥部发来的信息，敌军的轰炸机正朝着你所在的独木桥飞来！为了安全，你的部队必须撤下独木桥。独木桥的长度为

每个士兵都有一个初始面对的方向，他们会以匀速朝着这个方向行走，中途不会自己改变方向。但是，如果两个士兵面对面相遇，他们无法彼此通过对方，于是就分别转身，继续行走。转身不需要任何的时间。

由于先前的愤怒，你已不能控制你的士兵。甚至，你连每个士兵初始面对的方向都不知道。因此，你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外，总部也在安排阻拦敌人的进攻，因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。

输入格式

第一行：一个整数 $1\cdots L1⋯L。$

第二行：一个整数

第三行：有

输出格式

只有一行，输出

输入输出样例
输入 #1/span>
4
2
1 3
输出 #1
2 4
说明/提示

初始时，没有两个士兵同在一个坐标。

数据范围　　1=<L<=5000 　　0<N<=5000,保证N<L；

　　此题分别要求求出最长和最短时间，下面分别分析

　　　　最短时间:因为题目已经说明最初没有位置有两个人，所以只要每个人都向离自己最近的方向走，就可以做到最快撤离，最短时间为按这种方案撤离需要时间最长的人

　　　　最长时间：按照最短时间的方式思考，自然而然的得出当所有人都像离自己远的一端移动时，时间最长，但是当桥两边的士兵相向运动时，会出现许多的变化情况。如下图

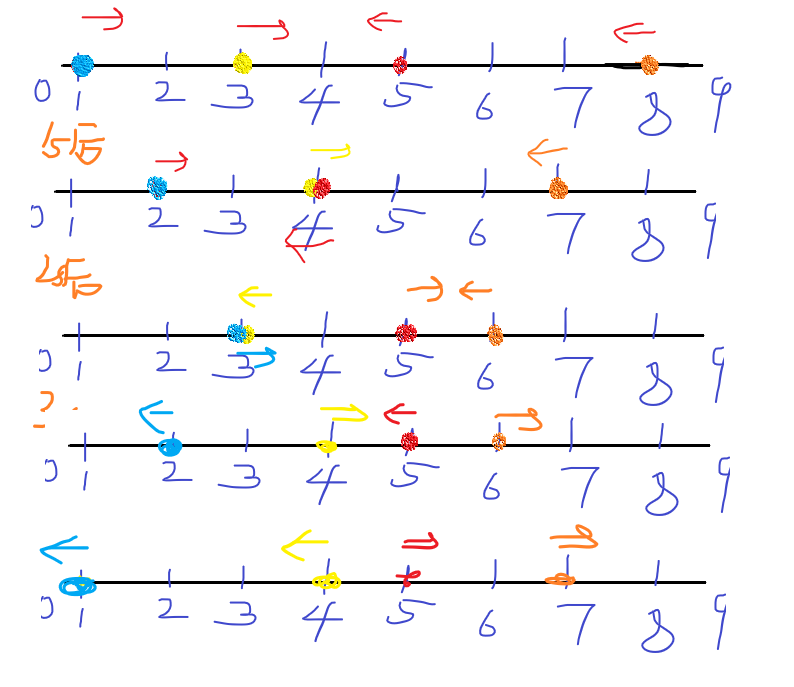
　　　　但由于所有相向运动最终都会回归为各自背向运动，所以最初的思路时 最长时间=达到背向运动的时间+达到背向运动状态时位置的最短时间

　　　　但是在实际编码过程中发现，求出状态变化过程的时间太过复杂。所以换了一种思路。以上的想法是把每个士兵看作有差异的个体，但是实际上我们需要的只是所有的士兵成功撤离，并不关心具体的某位士兵撤离到了那一边，

　　　　所以可以忽略相遇转向的过程，直接视为可以互相穿过

　　　　　　　　eg:最初的想法是这样的

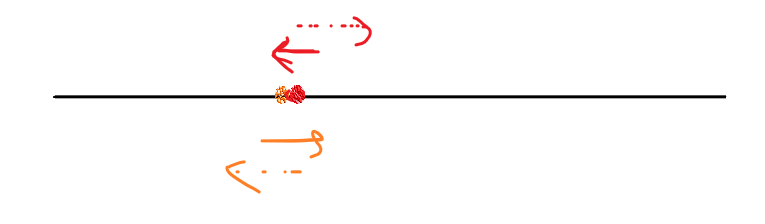
　　　　　　但是忽略士兵的不同之后可以看作

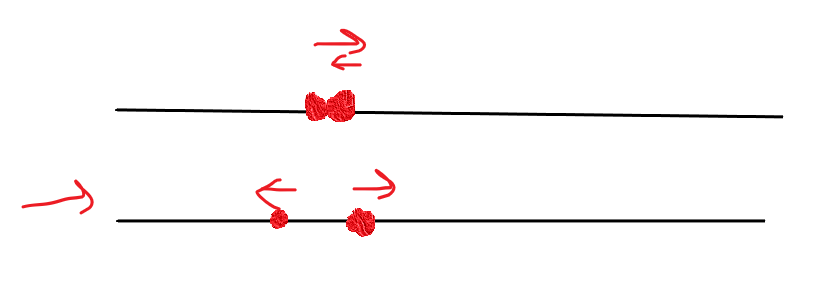
所以可以直接比较每位士兵到达较远端的时间，最大的一个即最长时间

　以下是代码

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int L,N,tmin=0,tmax=0;
    cin>>L;
    cin>>N;
    for(int i=0;i<N;i++)
    {
        int place;
        cin>>place;
        tmin=max(tmin,min(place,L+1-place));
        tmax=max(tmax,max(place,L+1-place));
    }
    cout<<tmin<<' '<<tmax;
    
}

P1008 [NOIP1998 普及组] 三连击

题目背景

本题为提交答案题，您可以写程序或手算在本机上算出答案后，直接提交答案文本，也可提交答案生成程序。

题目描述

将 $\ldots , 91,2,…,9 共 99 个数分成 33 组，分别组成 33 个三位数，且使这 33 个三位数构成 1 : 2 : 31:2:3 的比例，试求出所有满足条件的 33 个三位数。$

输入格式

无

输出格式

若干行，每行

输入输出样例

输入 #1
无

输出 #1

192 384 576
* * *
...

* * *
（剩余部分不予展示）

分析

　　　　最初看到本题，可能下意识是从分组的情况去思考，即先分组再比较值这一较为简单的思考方法，但是实际实行时发现如果先分组，只是进行随机分为三组的操作就已经极为复杂，而每一组的取值有需要经过循环来取得，最终还需要匹配各组产生的值，

　　难免让人感觉吃力不讨好。所以不如换一种思路，先取出所有三位数字各不相同的三位数，分别取其2倍和3倍，然后看这两个数的数字是否已经使用过，思路如此，以下时代码

#include<bits/stdc++.h>
using namespace std;
int number[10];//标记1---9的数字是否使用过。 
int isok(int num)
{
    //分解数字 
    int a,b,c;
    a=num/100;
    b=(num%100)/10;
    c=num%10;
    //判断是否使用过。 
    if(number[a]!=1&&number[b]!=1&&number[c]!=1)
    {
        number[a]=1;
        number[b]=1;
        number[c]=1;
        return 1;
    }
    else return 0;
}
int main()
{
    int num1,num2,num3;
    int i,j,z;
    for(i=1;i<=9;i++)
    {
        for(j=1;j<=9;j++)
        {    
            if(j!=i)
            for(z=1;z<=9;z++)
            {
                if(z!=i&&z!=j)//保证三位数字不同 
                {
                    //将每个使用过的数字标记 
                    number[i]=1;
                    number[j]=1;
                    number[z]=1;
                    num1=i*100+j*10+z;
                    num2=num1*2;
                    num3=num1*3;
                    //排除2倍或3倍不是三位数的情况 
                    if(num2>=1000||num3>=1000)
                    {
                        continue;
                    }
                    //判断2倍和3倍的结果的数字是否使用过 
                    if(isok(num2)&&isok(num3))
                    {
                        printf("%d %d %d\n",num1,num2,num3);
                    }
                    //当某一个num已经被验证之后将标记数组归0，进行下一次循环。 
                    for(int l=1;l<10;l++)
                    {
                        number[l]=0;
                    }
                }
            }
        }
    }
}

P1009 [NOIP1998 普及组] 阶乘之和

题目描述

用高精度计算出

其中“!”表示阶乘，例如：

输入格式

一个正整数

输出格式

一个正整数

输入输出样例
输入 #1
3
输出 #1
9
说明/提示

【数据范围】

对于 $\%100% 的数据，1<=n<=50$

此题是典型的高精度计算，需要用到的是高精度乘法和高精度加法

　具体操作见高精度算法（乘法），加法

此处讲一些操作中的注意事项

　　由于进位的问题，建议所有的数据在最终输出之前，反向储存在数组中，防止如果最高位需要进位的话，需要移动整个数组。
进位的过程中 if(a[i]>=10){a[i+1]+=a[i]/10，a[i]=a[i]%10}中判断语句中的‘=’不能忘记,否则容易出现最后相加时发现数组溢出
最后如果是算法题，建议直接开出几个足够大的数组，可以极大的加快编码速度（自己编码的时候没想到可以直接开大数组，选择了直接用vector<int>类来进行动态分配，感觉算法很明显但是编码过程用了很久）Ｏ(≧口≦)Ｏ

　　下面是我的代码（看过题解总感觉自己写成这样很蠢 ,可恶！！！！！(〃＞目＜) )、

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
vector<int> getSum(vector<int>a, vector<int>b);
void getSumfactorial(int n, vector<int>* result);
vector<int> getfactorial(int n);
vector<int> getproduct(vector<int> result, int num);
vector<int> getSum(vector<int>a, vector<int>b);
int main()
{
    int n;
    vector<int> result;
    cin >> n;
    getSumfactorial(n, &result);
    for (int i = 0; i < result.size(); i++)
    {
        cout << result[i];
    }
    cout << endl;
    return 0;
}
//求阶乘和 
void getSumfactorial(int n, vector<int>* result)
{
    int i;
    vector<int>a;
    vector<int>b;
    b.push_back(0);
    for (i = 1; i <= n; i++)
    {
        a = getfactorial(i);
        b = getSum(a, b);
    }
    for (i = b.size() - 1; i >= 0; i--)
    {
        (*result).push_back(b[i]);
    }
    if ((*result).back() >= 10)
    {
        (*result).push_back(0);
    }
    for (i = 0; i < result->size(); i++)
    {
        if ((*result)[i] >= 10)
        {
            (*result)[i + 1] += (*result)[i] / 10;
            (*result)[i] = (*result)[i] % 10;
        }
    }
}
//求阶乘 
vector<int> getfactorial(int n)
{
    vector<int> result;
    int i;
    result.push_back(1);
    for (i = 1; i <= n; i++)
    {
        result = getproduct(result, i);
    }
    return result;
}
//将整数转化为数组
void changetovector(int num, vector<int>* cs)
{
    while (num / 10 > 0)
    {
        cs->push_back(num % 10);
        num = num / 10;
    }
    cs->push_back(num);
}
// 高精乘法 
vector<int> getproduct(vector<int> result, int num)
{
    vector<int> cs;//乘数 
    changetovector(num, &cs);
    int L1 = result.size();
    int L2 = cs.size();
    int Lc;
    if (result[L1 - 1] * cs[L2 - 1] >= 10)
    {
        Lc = L1 + L2;
    }
    else Lc = L1 + L2 - 1;
    int* c;
    c = new int[Lc];
    for (int i = 0; i < Lc; i++)
    {
        c[i] = 0;
    }
    for (int i = 0; i < L1; i++)
    {
        for (int j = 0; j < L2; j++)
            c[i + j] += result[i] * cs[j];
    }
    for (int i = 0; i < Lc - 1; i++)
    {
        if (c[i] >= 10)
        {
            c[i + 1] += c[i] / 10;
            c[i] = c[i] % 10;
        }
    }
    result.clear();
    for (int i = 0; i < Lc; i++)
    {
        result.push_back(c[i]);
    }
    return result;
}

vector<int> getSum(vector<int>a, vector<int>b)
{
    int i;
    vector<int> res;
    int La = a.size();
    int Lb = b.size();
    if (La < Lb)
    {
        for (i = La; i < Lb; i++)
        {
            a.push_back(0);
        }
    }
    if (Lb < La)
    {
        for (i = Lb; i < La; i++)
        {
            b.push_back(0);
        }
    }
    int bigger = max(La, Lb);
    for (i = 0; i < bigger; i++)
    {
        if (i < res.size())
            res[i] = a[i] + b[i];
        else
            res.push_back(a[i] + b[i]);
    }
    if (res.back() >= 10)
    {
        res.push_back(0);
    }
    for (i = 0; i < res.size(); i++)
    {
        if (res[i] >= 10)
        {
            res[i + 1] += res[i] / 10;
            res[i] = res[i] % 10;
        }
    }
    return res;
}

感觉还可以利用存储状态的方法优化以下求阶乘的过程，不需要每个阶乘都重复求，但是可能要等之后有空才能尝试了 ┑(￣Д ￣)┍

最后贴以下题解大佬的代码，○|￣|_

#include<stdio.h>
int main()
{
    int i,A[1005]={0},B[1005]={0},n,j;
    scanf("%d", &n);
    A[0]=B[0]=1;
    for (i=2;i<=n;i++){
        for (j=0;j<100;j++)
            B[j]*=i;
        for (j=0;j<100;j++)
            if (B[j]>9){
                B[j+1] += B[j]/10;
                B[j]%=10;
            }
        for (j=0;j<100;j++){
            A[j]+=B[j];
            if (A[j]>9) {
                A[j+1] += A[j]/10;
                A[j]%=10;
            }
        }
    }
    for (i=100;i>=0&&A[i]==0;i--);
    for (j=i;j>=0;j--) printf("%d", A[j]);
    return 0;
}

posted @ 2022-04-13 23:55 比奇堡的黄色小海绵阅读(142) 评论(0) 收藏举报

刷新页面返回顶部

zz-gy

洛谷刷题（一）

题目背景

题目描述

输入格式

输出格式

输入输出样例

说明/提示

P1008 [NOIP1998 普及组] 三连击

题目背景

题目描述

输入格式

输出格式

输入输出样例

P1009 [NOIP1998 普及组] 阶乘之和

题目描述

输入格式

输出格式

输入输出样例

说明/提示

下面是我的代码（看过题解总感觉自己写成这样很蠢 ,可恶！！！！！(〃＞目＜) )、

感觉还可以利用存储状态的方法优化以下求阶乘的过程，不需要每个阶乘都重复求，但是可能要等之后有空才能尝试了 ┑(￣Д ￣)┍

公告