浅谈激活函数以及其发展

激活函数是神经网络的相当重要的一部分，在神经网络的发展史上，各种激活函数也是一个研究的方向。我们在学习中，往往没有思考过——为什么用这个函数以及它们是从何而来？

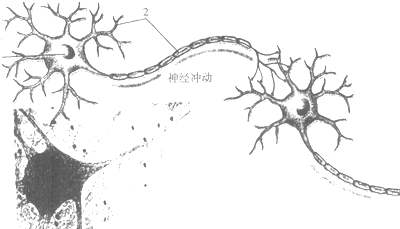
生物神经网络曾给予了人工神经网络相当多的启发。如上图，来自树突信号不断累积，如若信号强度超过一个特定阈值，则向轴突继续传递信号。如若未超过，则该信号被神经元“杀死”，无法继续传播。

在人工神经网络之中，激活函数有着异曲同工之妙。试想，当我们学习了一些新的东西之后，一些神经元会产生不同的输出信号，这使得神经元得以连接。

sigmoid函数也许是大家初学神经网络时第一个接触到的激活函数，我们知道它有很多良好的特性，诸如能将连续的实值变换为0到1的输出、求导简单，那么这个函数是怎么得到的呢？本文从最大熵原理提供一个角度。

sigmoid函数与softmax函数

最大熵原理与模型

最大熵原理是概率模型学习的一个准则¹。最大熵原理认为，学习概率模型时，在所有可能的概率模型中，熵最大的模型是最好的模型。

假设离散随机变量\(X\)的概率分布是\(P(X)\)，则其熵是

\[H(P)=-\sum_{x}P(x)\log P(x) \]

熵满足下列不等式：

\[0\leqslant H(P)\leqslant \log |X| \]

式中，\(|X|\)是\(X\)的取值个数，当且仅当\(X\)的分布是均匀分布时右边的等号成立。这就是说，当\(X\)服从均匀分布时，熵最大。

直观而言，此原理认为要选择的概率模型首先必须满足已有的条件，在无更多信息的条件下没其他不确定的部分都是等可能的。

假设分类模型是一个条件概率分布\(P(Y\mid X)\)，给定一个训练集\(T=\left\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\right\}\)，可以确定\(P(X, Y)\)的经验分布和边缘分布\(P(X)\)的经验分布，分别以\(\tilde{P}(X,Y)\)和\(\tilde{P}(X)\)表示。

用特征函数（feature function）\(f(x.y)\)描述输入\(x\)和\(y\)之间的某一个事实，定义为：

\[f(x, y)=\left\{\begin{array}{ll} 1, & x \text { 与 } y \text { 满足某一事实 } \\ 0, & \text { 否则 } \end{array}\right. \]

由上述信息，可以假设\(f(x.y)\)关于经验分布\(\tilde{P}(X,Y)\)的期望值和关于模型\(P(Y\mid X)\)与经验分布\(\tilde{P}(X)\)的期望值相等，即：

\[\sum_{x, y} \tilde{P}(x, y) f_{i}(x, y)=\sum_{x, y} \tilde{P}(x) P(y \mid x) f_{i}(x, y) \]

结合 条件，该问题等价于约束最优化问题：

\[\begin{aligned} &\min _{P \in \mathbf{C}} - H(P)=\sum_{x, y} \tilde{P}(x) P(y \mid x) \log P(y \mid x)\\ \text { s.t. } &\quad E_{P}\left(f_{i}\right)=E_{\tilde{P}}\left(f_{i}\right), \quad i=1,2, \cdots, n\\ &\sum_{y} P(y \mid x)=1 \end{aligned} \]

由拉格朗日乘子法，问题转换为求如下式子的最小值

\[\begin{equation} L=\sum_{x, y} \tilde{P}(x) P(y \mid x) \ln P(y \mid x)-w_{0}\left(\sum_{y} P(y \mid x)-1\right)-\sum_{i} w_{i}\left(\sum_{x, y} \tilde{P}(x, y) f_{i}(x, y)\right. \left.-\sum_{x, y} \tilde{P}(x) P(y \mid x) f_{i}(x, y)\right) \end{equation} \]

此时，我们对\(L\)求\(P(Y|X)\)的导数：

\[\begin{aligned} \frac{\partial{L}}{\partial P(y \mid x)} &=\sum_{x,y}\tilde{P}(x)(\log P(y \mid x)+1)-\sum_{x,y}w_{0}+\sum_{i} w_{i}(x) \tilde{P}(x) f_{i}(x, y) \\ &=\sum_{x,y}\tilde{P}(x)\left((\log P(y \mid x)+1)-w_{0}+\sum_{i} w_{i}(x) f_{i}(x, y)\right) \end{aligned} \]

令其导数值为0，在\(\tilde{P}(X) > 0\)的情况下，解得：

\[P(y\mid x)= \exp \left( \sum_{i=1}^{n} w_if_i(x,y)+w_0-1 \right) \]

由于\(\sum_{y}P(y\mid x)=1\)，得：

\[\begin{aligned} \sum_{y}P(y\mid x) &= \sum_{y}\exp \left( \sum_{i=1}^{n} w_if_i(x,y)+w_0-1 \right) \\ &=\frac{\sum_{y}\exp \left( \sum_{i=1}^{n} w_if_i(x,y) \right)}{\exp(1-w_0)} = 1 \end{aligned} \]

由上面两式可得：

\[P(y \mid x)=\frac{e^{-\sum_{i} w_{i} f_{i}(x, y)}}{\sum_{y} e^{-\sum_{i} w_{i} f_{i}(x, y)}} \]

细心的同学不难发现，这和softmax函数十分相近，定义\(f_i(x,y)=x\)，即可得到softmax函数：

\[P(y \mid x)=\frac{e^{-\sum_{i} w_{i} x}}{\sum_{y} e^{-\sum_{i} w_{i} x}} \]

那么sigmoid函数呢？其实该函数就是softmax函数的二分类特例：

\[P(y=1 \mid x)=\frac{1}{1+e^{\sum_{i} w_{i} x}} \]

说完了推导，就来谈谈这两函数的特点。sigmoid函数的优点前文已提到，但sigmoid在反向传播时容易出现“梯度消失”的现象。

可以看出，当输入值很大或很小时，其导数接近于0，它会导致梯度过小无法训练。

ReLU函数族的崛起

如图所示，ReLU函数很好避免的梯度消失的问题，与Sigmoid/tanh函数相比，ReLU激活函数的优点是：

• 使用梯度下降（GD）法时，收敛速度更快 。

• 相比ReLU只需要一个门限值，即可以得到激活值，计算速度更快 。

  缺点是： ReLU的输入值为负的时候，输出始终为0，其一阶导数也始终为0，这样会导致神经元不能更新参数，也就是神经元不学习了，这种现象叫做“Dead Neuron”。

为了解决ReLU函数这个缺点，又出现了不少基于ReLU函数的发展，比如Leaky ReLU(带泄漏单元的ReLU)、 RReLU（随机ReLU）等等，也许你有一天也能发现效果更好的ReLU函数呢！

引用

[1] [李航. 统计学习方法[M]. 清华大学出版社, 2012.]