【Python】时间序列分析完整过程

1. 导言

1.1 基本定义

根据维基百科上对时间序列的定义，我们简单将其理解为：

时间序列：一系列以时间顺序作为索引的数据点的集合。

因此，时间序列中的数据点，是围绕着相对确定的时间戳组织在一起的，与随机样本相比，它们包含了一些我们待提取的其他信息。

咱们先来看看，对时间序列数据分析，需要用到哪些库吧 ~

import numpy as np                               # 向量和矩阵运算
import pandas as pd                              # 表格与数据处理
import matplotlib.pyplot as plt                  # 绘图
import seaborn as sns                            # 更多绘图功能
sns.set()

from dateutil.relativedelta import relativedelta # 日期数据处理
from scipy.optimize import minimize              # 优化函数

import statsmodels.formula.api as smf            # 数理统计
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scs

from itertools import product                    # 一些有用的函数
from tqdm import tqdm_notebook

import warnings                                  # 勿扰模式
warnings.filterwarnings('ignore'

作为例子，本文以真实手游数据为例，来看一下我们玩家每小时观看的广告量和每天的游戏币消费情况这两个时间序列数据：

ads = pd.read_csv('../../data/ads.csv', index_col=['Time'], parse_dates=['Time'])
currency = pd.read_csv('../../data/currency.csv', index_col=['Time'], parse_dates=['Time'])

plt.figure(figsize=(15, 7))
plt.plot(ads.Ads)
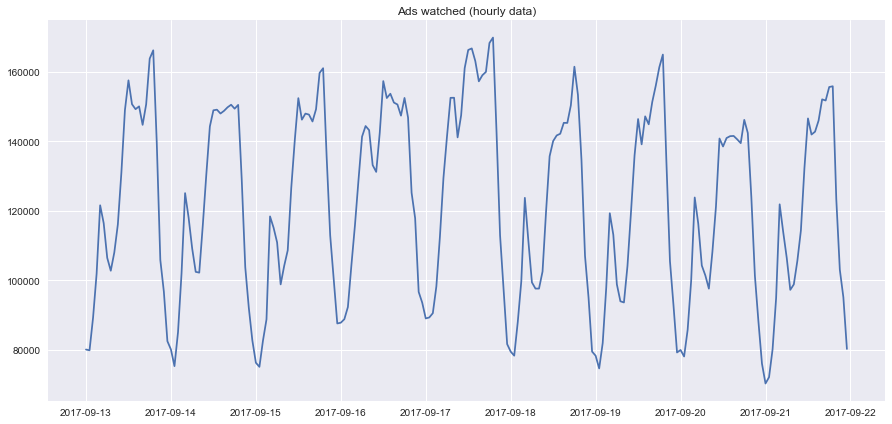
plt.title('Ads watched (hourly data)')
plt.grid(True)
plt.show()

plt.figure(figsize=(15, 7))
plt.plot(currency.GEMS_GEMS_SPENT)
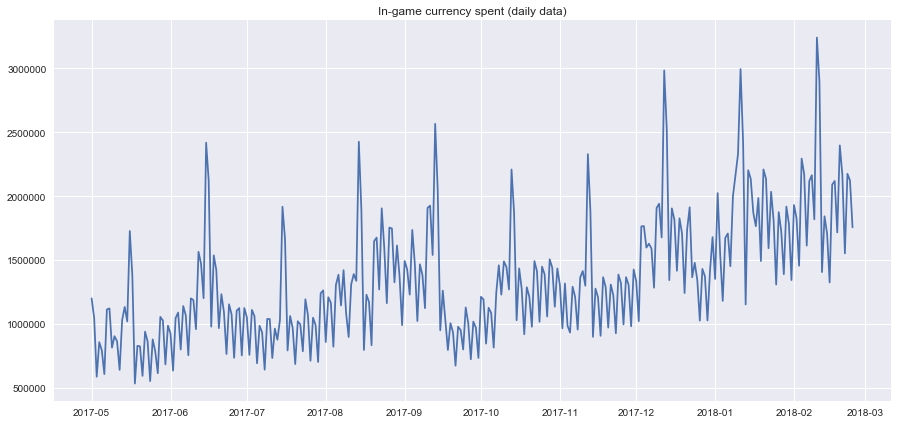
plt.title('In-game currency spent (daily data)')
plt.grid(True)
plt.show()

玩家在2017-09-13到2017-09-22这十天内，每小时广告阅读量的折线图：

玩家在2017-05到2018-03这十一个月内，每天游戏币消费的折线图：

1.2 预测评估指标

在我们开始预测时间序列数据之前，先来了解一些比较流行的模型评估指标。

R squared： $R^2R2 分数，表示确定系数（在计量经济学中，它可以理解为描述模型方差的百分比），描述模型的泛化能力，取值区间 ( − i n f , 1 ] (-inf, 1](−inf,1]，值为1时模型的性能最好；sklearn.metrics.r2_score$
Mean Absolute Error：平均绝对值损失，一种预测值与真实值之间的度量标准，也称作 $l_1l1-norm 损失，取值区间 [ 0 , + i n f ) [0,+inf)[0,+inf)；sklearn.metrics.mean_absolute_error$
Median Absolute Error：绝对值损失的中位数，抗干扰能力强，对于有异常点的数据集的鲁棒性比较好，取值区间 $[0,+inf)[0,+inf)；sklearn.metrics.median_absolute_error$
Mean Squared Error：均方差损失，常用的损失度量函数之一，对于真实值与预测值偏差较大的样本点给予更高（平方）的惩罚，反之亦然，取值区间 $[0,+inf)[0,+inf)；sklearn.metrics.mean_squared_error$
Mean squared logarithmic error：均方对数误差，定义形式特别像上面提的MSE，只是计算的是真实值的自然对数与预测值的自然对数之差的平方，通常适用于 target 有指数的趋势时，取值区间 $[0,+inf)[0,+inf)；sklearn.metrics.mean_squared_log_error$
Mean Absolute Percentage Error：作用和MAE一样，只不过是以百分比的形式，用来解释模型的质量，但是在sklearn的库中，没有提供这个函数的接口，取值区间

导入上面提到的损失度量函数：

from sklearn.metrics import r2_score, median_absolute_error, mean_absolute_error
from sklearn.metrics import median_absolute_error, mean_squared_error, mean_squared_log_error

def mean_absolute_percentage_error(y_true, y_pred): 
    return np.mean(np.abs((y_true - y_pred) / y_true)) * 100

2. 移动、平滑、评估

2.1 滑动窗口估计

在开始学习时序预测之前，我们得先做一个基本的假设，即 “明天将和今天一样” ，但是并不是用类似 $\hat{y}_{t}=y_{t-1}y^t=yt−1 的形式（虽然说这种方式可以作为一个baseline在时序数据的预测中）。$

2.1.1 moving average

我们假设未来某个值的预测，取决于它前面的 n 个数的平均值，因此，我们将用 moving average (移动平均数) 作为 target 的预测值，数学表达式为： $\hat{y}_{t}=\frac{1}{k} \sum_{n=0}^{k-1} y_{t-n}y^t=k1n=0∑k−1yt−n 用 numpy.average() 函数实现上述的功能：$

def moving_average(series, n):
    """
        Calculate average of last n observations
    """
    return np.average(series[-n:])

moving_average(ads, 24) # 对过去24小时的广告浏览量的预测

不幸的是，上面这种方式，不适合我们进行长期的预测（为了预测下一个值，我们需要实际观察的上一个值）。但是移动平均数还有另一个应用场景，即对原始的时间序列数据进行平滑处理，以找到数据的变化趋势。

pandas 提供了一个实现接口DataFrame.rolling(window).mean()，滑动窗口 window 的值越大，意味着变化趋势将会越平滑，对于那些噪音点很多的数据集（尤其是金融数据），使用 pandas的这个接口，有助于探测到数据中存在的共性（common pattern）。

def plotMovingAverage(series, window, plot_intervals=False, scale=1.96, plot_anomalies=False):

    """
        series - dataframe with timeseries
        window - rolling window size 
        plot_intervals - show confidence intervals
        plot_anomalies - show anomalies 
    """
    rolling_mean = series.rolling(window=window).mean()

    plt.figure(figsize=(15,5))
    plt.title("Moving average\n window size = {}".format(window))
    plt.plot(rolling_mean, "g", label="Rolling mean trend")

    # Plot confidence intervals for smoothed values
    if plot_intervals:
        mae = mean_absolute_error(series[window:], rolling_mean[window:])
        deviation = np.std(series[window:] - rolling_mean[window:])
        lower_bond = rolling_mean - (mae + scale * deviation)
        upper_bond = rolling_mean + (mae + scale * deviation)
        plt.plot(upper_bond, "r--", label="Upper Bond / Lower Bond")
        plt.plot(lower_bond, "r--")
        
        # Having the intervals, find abnormal values
        if plot_anomalies:
            anomalies = pd.DataFrame(index=series.index, columns=series.columns)
            anomalies[series<lower_bond] = series[series<lower_bond]
            anomalies[series>upper_bond] = series[series>upper_bond]
            plt.plot(anomalies, "ro", markersize=10)
        
    plt.plot(series[window:], label="Actual values")
    plt.legend(loc="upper left")
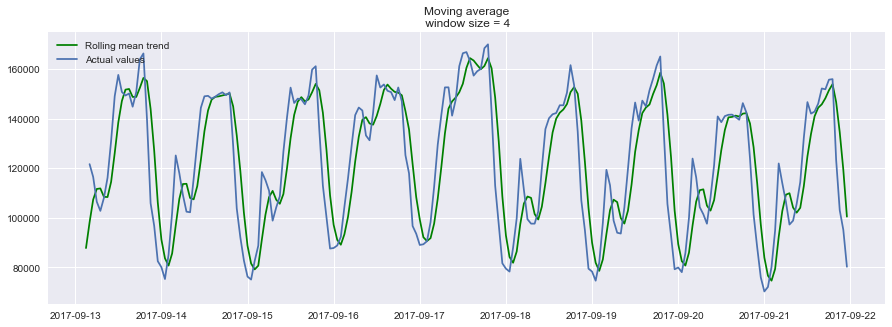
    plt.grid(True)

设置滑动窗口值为4(小时)，plotMovingAverage(ads, 4)，绘制预测结果：
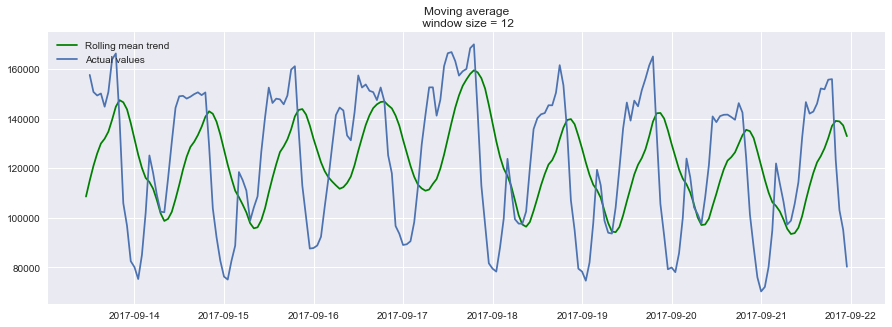
设置滑动窗口值为12(小时)，plotMovingAverage(ads, 12)，绘制预测结果：
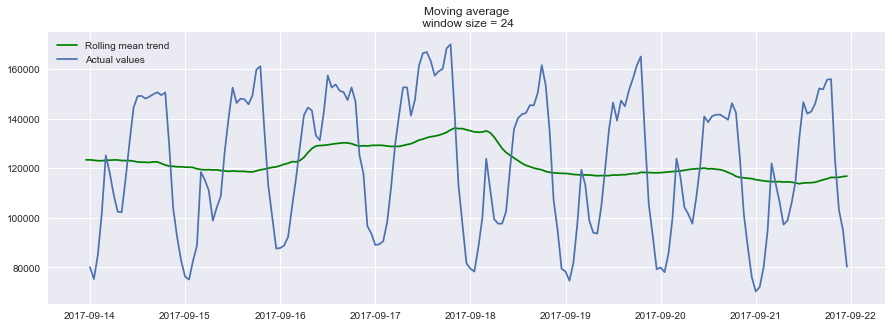
设置滑动窗口值为24(小时)，plotMovingAverage(ads, 24)，绘制预测结果：

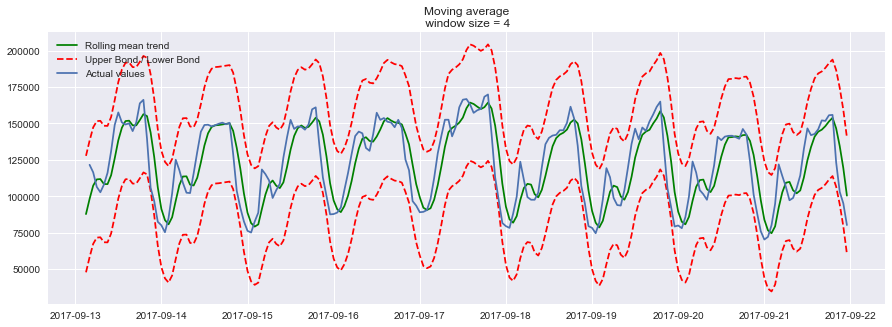
以24小时作为滑动窗口的大小，来分析玩家每小时阅读广告量的信息时，可以清晰地发现广告浏览量的变化趋势，周末时广告浏览量较高，工作日广告浏览量较低。
我们还可以给我们的平滑值添上置信区间plotMovingAverage(ads, 4, plot_intervals=True)

现在我们再用 moving average 创建一个简单的异常检测系统（即如果数据点在置信区间之外，则认为是异常值），显然在我们上面的时间系列数据中，数据点都在置信区间以内，因此我们故意把数据中的某个值改为异常值。

ads_anomaly = ads.copy()
ads_anomaly.iloc[-20] = ads_anomaly.iloc[-20] * 0.2 # say we have 80% drop of ads

我们来瞧一下，上面这个简单的方法，是否能够找到异常值。
plotMovingAverage(ads_anomaly, 4, plot_intervals=True, plot_anomalies=True)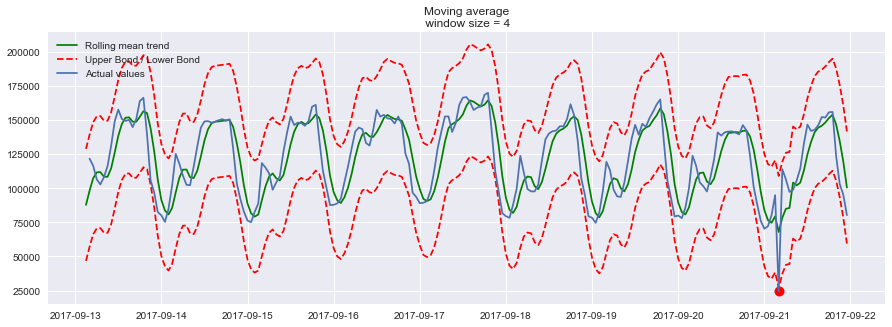

瞧！我们的方法，找到了异常点的位置（2017-09-21），那我们再来试试第二个数据序列（每天游戏币的消费情况），并且设置滑动窗口大小为7，看看是什么效果。
plotMovingAverage(currency, 7, plot_intervals=True, plot_anomalies=True)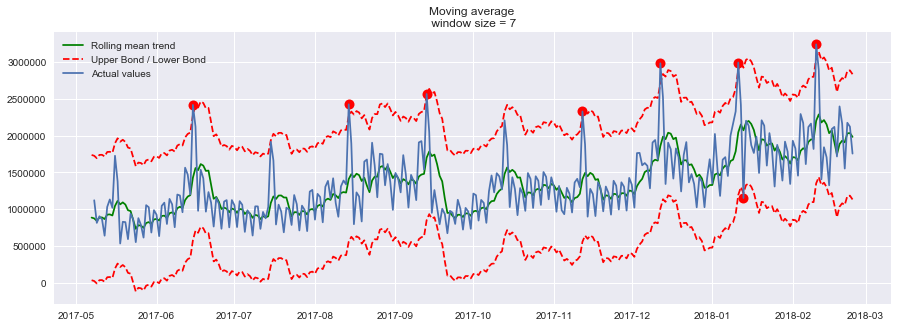

Oh no！这就暴露出我们简单方法的缺点了。它没有在我们的数据中捕捉到每个月中出现的季节性变化，反倒几乎把所有每隔30天出现的峰值标记为异常。

如果你不想有那么多的错误警报，那么最好考虑更复杂的模型。

2.1.2 weighted average

上面提到了用移动平均值对原始数据做平滑处理，接下来要说的是加权平均值，它是对上面移动平均值的简单改良。

也就是说，前面 k 个观测数据的值，不再是直接求和再取平均值，而是计算它们的加权和（权重和为1）。通常来说，时间距离越近的观测点，权重越大。数学表达式为：
$\hat{y}_{t}=\sum_{n=1}^{k} \omega_{n} y_{t+1-n}y^t=n=1∑kωnyt+1−n$

def weighted_average(series, weights):
    """
        Calculate weighter average on series
    """
    result = 0.0
    weights.reverse()
    for n in range(len(weights)):
        result += series.iloc[-n-1] * weights[n]
    return float(result)
  
  weighted_average(ads, [0.6, 0.3, 0.1])

2.2 指数平滑

2.2.1 exponential smoothing

如果不用上面提到的，每次对当前序列中的前k个数的加权平均值作为模型的预测值，而是直接对目前所有的已观测数据进行加权处理，并且每一个数据点的权重，呈指数形式递减。

这个就是指数平滑的策略，具体怎么做的呢？一个简单的数学式为：
$\hat{y}_{t}=\alpha \cdot y_{t}+(1-\alpha) \cdot \hat{y}_{t-1}y^t=α⋅yt+(1−α)⋅y^t−1 式子中的 α \alphaα 表示平滑因子，它定义我们“遗忘”当前真实观测值的速度有多快。α \alphaα 越小，表示当前真实观测值的影响力越小，而前一个模型预测值的影响力越大，最终得到的时间序列将会越平滑。（这个结论要记住哦，有助于理解接下来的绘图）$

那么指数体现在哪呢？指数就隐藏在递归函数之中，我们上面的函数，每次都要用 $(1-\alpha)(1−α)乘以模型的上一个预测值。$

def exponential_smoothing(series, alpha):
    """
        series - dataset with timestamps
        alpha - float [0.0, 1.0], smoothing parameter
    """
    result = [series[0]] # first value is same as series
    for n in range(1, len(series)):
        result.append(alpha * series[n] + (1 - alpha) * result[n-1])
    return result
    
def plotExponentialSmoothing(series, alphas):
    """
        Plots exponential smoothing with different alphas
        
        series - dataset with timestamps
        alphas - list of floats, smoothing parameters
        
    """
    with plt.style.context('seaborn-white'):    
        plt.figure(figsize=(15, 7))
        for alpha in alphas:
            plt.plot(exponential_smoothing(series, alpha), label="Alpha {}".format(alpha))
        plt.plot(series.values, "c", label = "Actual")
        plt.legend(loc="best")
        plt.axis('tight')
        plt.title("Exponential Smoothing")
        plt.grid(True);
        
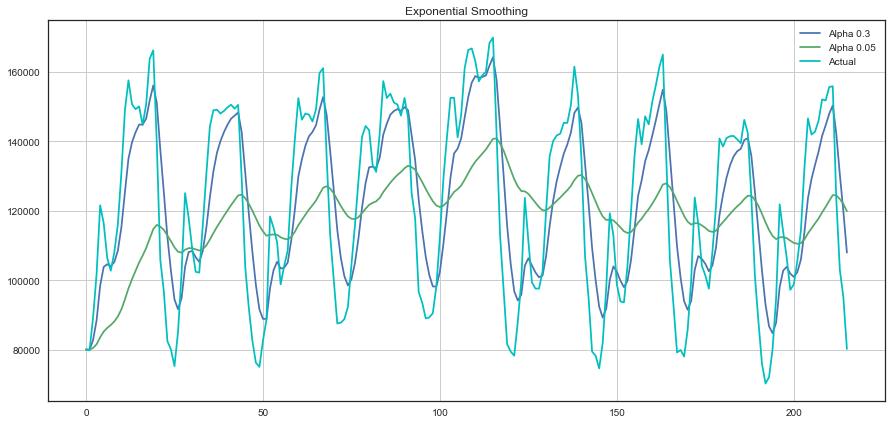
plotExponentialSmoothing(ads.Ads, [0.3, 0.05])
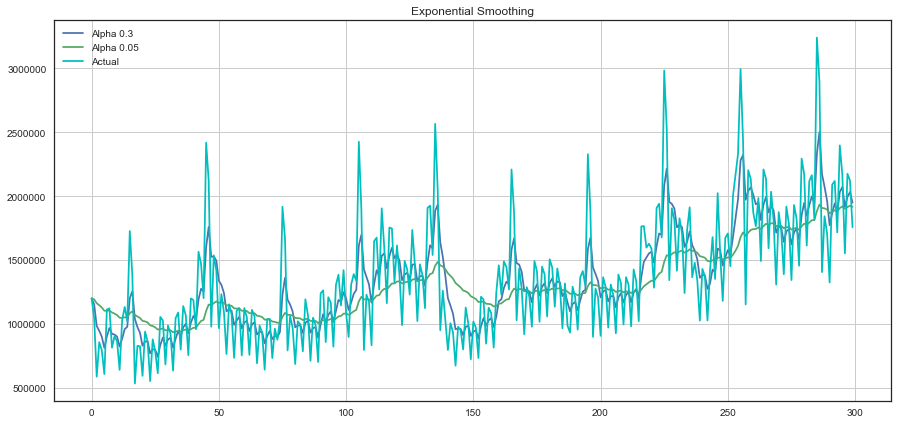
plotExponentialSmoothing(currency.GEMS_GEMS_SPENT, [0.3, 0.05])

游戏玩家每小时浏览的广告量在不同平滑因子下的时序图：
游戏玩家每天游戏币的消费量在不同平滑因子下的时序图：

单指数平滑小结

单指数平滑的特点：能够追踪数据变化。预测过程中，添加了最新的样本数据之后，新数据逐渐取代老数据的地位，最终老数据被淘汰。

单指数平滑的局限性：第一，预测值不能反映趋势变动、季节波动等有规律的变动；第二，这个方法多适用于短期预测，而不适合中长期的预测；第三，由于预测值是历史数据的均值，因此与实际序列相比，有滞后的现象。

单指数平滑的系数： EViews提供两种确定指数平滑系数的方法：自动给定和人工确定。一般来说，如果序列变化比较平缓，平滑系数值应该比较小，比如小于0.l；如果序列变化比较剧烈，平滑系数值可以取得大一些，如0.3～0.5。若平滑系数值大于0.5才能跟上序列的变化，表明序列有很强的趋势，不能采用一次指数平滑进行预测。

2.2.2 double exponential smoothing

前面在对于单指数平滑的小结中，提到了它的一些局限性。

单指数平滑在产生新的序列的时候，考虑了前面的 K 条历史数据，但是仅仅考虑其静态值，即没有考虑时间序列当前的变化趋势。

如果当前的时间序列数据处于上升趋势，那么当我们对明天的数据进行预测的时候，就不应该仅仅是对历史数据进行”平均“，还应考虑到当前数据变化的上升趋势。同时考虑历史平均和变化趋势，这个就是我们的双指数平滑法。

下面看看它具体是怎么做的：

通过序列分解法 (series decomposition)，我们可以得到两个分量，一个叫 intercept (also, level) $\ellℓ ，另一个叫 trend (also, slope，斜率) b bb. 我们根据前面学习的方法，知道了如何预测 intercept （截距，即序列数据的期望值），我们可以将同样的指数平滑法应用到 trend (趋势)上。时间序列未来变化的方向取决于先前加权的变化。ℓ x = α y x + ( 1 − α ) ( ℓ x − 1 + b x − 1 ) b x = β ( ℓ x − ℓ x − 1 ) + ( 1 − β ) b x − 1 y ^ x + 1 = ℓ x + b x$

ℓ x = α y x + (1 - α) (ℓ x - 1 + b x - 1)

第一个函数 $\ell_{x}ℓx 表示截距，第一项表示序列的当前值 y x y_{x}yx，第二项现在被拆分为 level 和 trend 的上一个值；$

第二个函数 $b_{x}bx 表示斜率(或趋势)，第一项为当前的截距值与上一个截距值之差，描述趋势的变化情况，第二项为趋势的前一个值。β系数表示指数平滑的权重；$

第三个函数 $\hat{y}_{x+1}y^x+1，表示最后序列的预测值，为截距和趋势的模型预测值之和；$

def double_exponential_smoothing(series, alpha, beta):
    """
        series - dataset with timeseries
        alpha - float [0.0, 1.0], smoothing parameter for level
        beta - float [0.0, 1.0], smoothing parameter for trend
    """
    # first value is same as series
    result = [series[0]]
    for n in range(1, len(series)+1):
        if n == 1:
            level, trend = series[0], series[1] - series[0]
        if n >= len(series): # forecasting
            value = result[-1]
        else:
            value = series[n]
        last_level, level = level, alpha*value + (1-alpha)*(level+trend)
        trend = beta*(level-last_level) + (1-beta)*trend
        result.append(level+trend)
    return result

def plotDoubleExponentialSmoothing(series, alphas, betas):
    """
        Plots double exponential smoothing with different alphas and betas
        
        series - dataset with timestamps
        alphas - list of floats, smoothing parameters for level
        betas - list of floats, smoothing parameters for trend
    """
    
    with plt.style.context('seaborn-white'):    
        plt.figure(figsize=(20, 8))
        for alpha in alphas:
            for beta in betas:
                plt.plot(double_exponential_smoothing(series, alpha, beta), label="Alpha {}, beta {}".format(alpha, beta))
        plt.plot(series.values, label = "Actual")
        plt.legend(loc="best")
        plt.axis('tight')
        plt.title("Double Exponential Smoothing")
        plt.grid(True)
        
  plotDoubleExponentialSmoothing(ads.Ads, alphas=[0.9, 0.02], betas=[0.9, 0.02])
  plotDoubleExponentialSmoothing(currency.GEMS_GEMS_SPENT, alphas=[0.9, 0.02], betas=[0.9, 0.02])

游戏玩家每小时浏览的广告量在不同平滑因子的组合下的时序图：
游戏玩家每天游戏币的消费量在不同平滑因子的组合下的时序图：

现在我们需要调整两个参数 $\alphaα 和 β \betaβ 。前者决定时间序列数据自身变化趋势的平滑程度，后者决定趋势的平滑程度（有点拗口，可自行观看上图来理解这句话）。$

2.2.3 Triple exponential smoothing

三指数平滑，也叫 Holt-Winters 平滑，与前两种平滑方法相比，我们这次多考虑了一个因素，seasonality （季节性）。这其实也意味着，如果我们的时间序列数据，不存在季节性变化，就不适合用三指数平滑。

模型中的季节性分量，用来解释截距和趋势的重复变化，并且由季节长度来描述，也就是变化重复的周期来描述。

对于一个周期内的每一个观测点，都有一个单独的组成部分。例如，如果季节长度为7（每周季节性），我们将有7个季节性组成部分，一个用于一周中的一天。

ℓ x = α (y x - s x - L) + (1 - α) (ℓ x - 1 +

第一个函数

$\ell_{x}$

第二个函数

$b_{x}$

第三个函数

$s_{x}$

第四个函数

$\hat{y}_{x+m}$

下面是三指数平滑模型的代码，也称Holt-Winters模型，得名于发明人的姓氏——Charles Holt和他的学生Peter Winters。此外，模型中还引入了Brutlag方法，以创建置信区间：

2.3 时间序列交叉验证

我们在常规的数据集中，都有用过交叉验证法，以找到模型最佳的参数。但是对于时间序列数据，数据间存在时间的依赖性，我们就不能再随机划分数据集，导致数据中的时间结构被破坏了。

因此，我们不得不使用一些技巧性的方法，这个方法叫做滚动交叉验证，可观察下面的式子，来理解这个方法。

fold 1 : training [1], test [2]
fold 2 : training [1 2], test [3]
fold 3 : training [1 2 3], test [4]
fold 4 : training [1 2 3 4], test [5]
fold 5 : training [1 2 3 4 5], test [6]

滚动交叉验证的图形表示：

现在，咱们知道了时间序列的数据，交叉验证集应该怎么划分。接下来开始动手找出 Holt-Winters 模型在玩家每小时的广告浏览量数据集中的最佳参数，我们根据常识可知，这个数据集中，存在一个明显的季节性变化，变化周期为24小时，因此我们设置 slen = 24 :

在 Holt-Winters 模型以及其他指数平滑模型中，对平滑参数的大小有一个限制，每个参数都在0到1之间。因此我们必须选择支持模型参数约束的最优化算法，在这里，我们使用 Truncated Newton conjugate gradient (截断牛顿共轭梯度法)

将上面训练后得到的最优参数组合（三个平滑系数），绘制图形：

玩家每小时广告浏览量在三指数平滑模型下的预测图：

玩家每小时广告浏览量在三指数平滑模型下的异常点检测图：

从图表判断，我们的模型能够成功地逼近初始时间序列，捕捉到日季节性、整体下降趋势甚至一些异常。如果你看一下模型的偏差(deviation)，你可以清楚地看到模型对序列结构的变化反应非常强烈，但是很快就会把偏差恢复到正常值，“遗忘”过去。(参看下面折线图) 该模型的这一特性允许我们快速构建异常检测系统，即使对于非常嘈杂的系列，也不需要花费太多的时间和金钱来准备数据和训练模型。

广告每小时浏览量的模型偏差（deviation）走势图：

我们把同样的方法，用于第二个时间序列（玩家每天游戏币的消费情况），这里我们把季节性周期设置为 30 ，即 slen = 30 ：

玩家每天游戏币的消费情况在三指数平滑模型下的预测图：

玩家每天游戏币的消费情况在三指数平滑模型下的异常点检测图：

玩家每天游戏币的消费情况模型的偏差（deviation）走势图：

3. 计量经济学方法

3.1 平稳性

在我们开始建模之前，我们需要提到时间序列的一个重要特性，如平稳性 (stationarity)。

我们称一个时间序列是平稳的，是指它不会随时间而改变其统计特性，即平均值和方差不会随时间而改变。

下图中，红色的序列是不平稳的，因为它的均值随着时间增加；

，红色的序列是不平稳的，因为它的均值随着时间增加；

下图中，红色的序列是不平稳的，因为随着时间的增加，序列点越来越靠近，所以它的协方差也不是一个常数；

那么为什么平稳性这么重要呢？

因为现在大多数的时间序列模型，或多或少都是基于未来序列与目前已观测到的序列数据有着相同的统计特性(均值、方差等) 的假设。也就是说，如果原始序列（已观测序列）是不平稳的，那么我们现有模型的预测结果，就可能会出错。

3.2 摆脱平稳性

首先呢，咱们得知道，导致原始序列不平稳的数据点在哪。为了做到这一点，我们来看看白噪声和随机游走。

绘制白噪声图：

上面是通过标准正态分布生成所生成的样本点，所以它们的分布显然是平稳的，均值为0，方差为1。

$\mathrm{x}(\mathrm{t})=\rho^{*} \mathrm{x}(\mathrm{t}-1)+\mathrm{e}(\mathrm{t})$

绘制新的样本点分布图：

$\rho=0$

上述情况出现的原因，是因为当到达了临界值之后，时间序列

$\mathrm{x}(\mathrm{t})=\rho^{*} \mathrm{x}(\mathrm{t}-1)+\mathrm{e}(\mathrm{t})$

$\mathrm{x}(\mathrm{t}) - \mathrm{x}(\mathrm{t}-1)=(\rho-1)^{*} \mathrm{x}(\mathrm{t}-1)+\mathrm{e}(\mathrm{t})$

等式左边，我们称之为一阶差分 (first difference)，如果

$\rho=1$

需要指出的是，一阶差分并不总是足以得到平稳序列，因为可能是d阶单整且d > 1（具有多个单位根），在这样的情形下，需要使用增广迪基-福勒检验（augmented Dickey-Fuller test）。

我们可以使用不同的方法来对抗非平稳性，如 d阶差分、趋势和季节性消除、平滑处理，也可以使用像box cox或对数这样的转换。

3.3 SARIMA模型构建

现在呢，我们可以通过经历让原始序列平稳的每一个阶段，来构建一个 SARIMA 模型。

绘制时间序列图、ACF 图和 PACF 图代码：

出乎意料，初始序列是平稳的，迪基-福勒检验拒绝了单位根存在的零假设。实际上，从上面的图形本身就可以看出这一点——没有明显的趋势，所以均值是恒定的，整个序列的方差也相对比较稳定。在建模之前我们只需处理季节性。为此让我们采用“季节差分”，也就是对序列进行简单的减法操作，时差等于季节周期。

观察上图，图表中可见的季节性消失，但是自相关 (autocorrelation) 函数仍然有太多的明显滞后的情况(图中浅色阴影之外的一些点为滞后点)。为了移除它们，我们将取一阶差分：从序列中减去自身（时差为1）

可以看到，我们的序列可以看到是在零周围振荡，迪基-福勒检验表明它是平稳的，ACF中显著的尖峰不见了。我们终于可以开始建模了！

3.4 ARIMA模型的速成教程

我们逐字母地来理解

$\operatorname{SARIMA}(p, d, q)(P, D, Q, s)$

此时，

$\mathrm{AR}(p)+\mathrm{MA}(q)=\mathrm{ARMA}(p, q)$

加上字母 I 之后，我们得到了 ARIMA 模型，可以通过非季节性差分处理非平稳数据。

$\mathrm{S}(s)$

现在，我们的模型

$\operatorname{SARIMA}(p, d, q)(P, D, Q, s)$

现在我们知道了如何设置初始的参数值，那我们再最后看一遍图表，然后找到模型上述的参数。

观察可得：

那么我们现在对 SARIMA 模型的参数进行搜索，看哪一组参数效果最好：

1. 设置参数搜索区间：

2. 寻找 SARIMA 模型的最佳参数组合：

30
31
32
33
34
35
36
37
3. 设置 SARIMA 模型最佳参数，查看模型输出结果：

4. 我们绘制模型的残差分布情况：

5. 很明显，模型的残差是平稳的，没有明显的自相关，让我们用此模型进行预测.

最后，我们得到了相当充分的预测，我们的模型平均错误率为4.01%，这是非常好的，但是准备数据，使得原始序列平稳和蛮力参数选择的总成本可能不值得这个精度。

4. 时间序列的（非）线性模型

在工作中，构建模型的原则是快、好、省。这也就意味着有些模型并不适合用于生产环境。

因为它们需要过长的数据准备时间，或者需要频繁地重新训练新数据，或者很难调整参数（前面提到的 SARIMA 模型就包含了着三个缺点）。

因此，我们一般使用一些轻松得多的方法，比如说从现有时间序列中选取一些特征，然后创建一个简单的线性回归或随机森林模型。

4.1 特征提取

咱们来分析一下，现在我们所拥有的只是一个一维时间序列。它能有哪些可以提取的特征呢？

时间序列的滞后值
窗口相关统计量
一个窗口序列中的最大值/最小值；
一个窗口序列中的平均值和中位数；
窗口的方差；
日期和时间特征
每小时的第几分钟，每天的第几小时，每周的第几天；
这一天是节假日吗？有什么特别的事情发生了吗？这可以作为布尔值特征；
目标值编码
其他模型的预测值

咱们再来看看，能否从广告浏览量的序列数据中，通过上面的一些方法，提取出某些特征。

4.1.1 时间序列的滞后值

将时间序列来回移动 n 步，我们能得到一个特征，其中时序的当前值和其t-n时刻的值对齐。如果我们移动1时差，并训练模型预测未来，那么模型将能够提前预测1步。增加时差，比如，增加到6，可以让模型提前预测6步，不过它需要在观测到数据的6步之后才能利用。

1
2
3
4
5
6
7
咱们现在有了数据集了，那先用线性回归训练一个模型试试吧！

简单的处理，效果还不是很差，但是里面有大量不必要的特征，咱们继续来做特征工程。

4.1.2 日期和时间特征

我们将在数据集中加入小时、星期几、是否周末三个特征。为此我们需要转换当前dataframe的索引为datetime格式，并从中提取hour和weekday。

我们可以可视化上面得到的特征：

（蓝线：小时；绿线：星期几；红色：是否周末）

现在我们需要对上述特征进行归一化处理：

测试集上的误差下降了一点，根据系数图判断，我们可以发现工作日和周末是很有用的特征。

4.1.3 平均值编码

我们可以在已有的特征空间中，再添加一个对类别型变量进行编码的变体，平均值编码。

如果使用大量的dummy变量来分解数据集，则会导致有关距离的信息丢失，并且它们不能被当作实数值，如 “0点 < 23 点”，而实际上第二天的 0 点比前一天的 23 点大。

因此我们应该用一些更易于解释的值对变量进行编码，自然而然的想法就是平均值编码。

举个例子，我们把所有特征值为星期三的广告阅读量累加起来，再取平均值，然后用该值覆盖原本特征值。（实际做法是生成字典结构，key为星期几，value为target的均值，生成新的特征字段，再drop掉原来的类别型特征）

聚类计算均值

1
2
3
4
5
6
以 hours 字段为例

把上面提到的三种转换，集成在下面的一个函数中：

线性回归模型的预测图：

线性回归模型的权重系数：

我们可以看到，hour_average 这个特征的系数比起其他的特征，显得太大了，以至于其他特征在模型的计算中，所起到的作用变得很小。解决这个问题的办法有很多，比如说我们可以不在整个训练集上进行target的平均值编码，而是在相应的滑动窗口上进行计算。或者说我们直接手动移除这种特征，反正我们确定它只会带来更多的坏处。

4.2 正则化与特征筛选

我们都知道，并不是每一个特征都是重要的，有些特征甚至会带来过拟合，像这种特征应该被移除。除此之外，我们还要尝试正则化方法，两种常见的带正则化的线性回归模型分别是 Lasso(

$l_1$

绘制特征热度图，删除相关度比较高的特征

Ridge(

$l_2$

Ridge 预测结果：

Ridge 权重分布观察发现，Ridge的参数分布相对比较均匀，并且那些不太重要的特征，系数越来越趋向于0；

Lasso(