算法入门——二分：快速幂

快速幂

一、问题描述

　　现在假设写一个程序计算2^18，那么可以得到代码

　　　　for(int i=0;i<18;i++) a=a*2;//a的初值为1。

　　这个代码可以很轻松的跑出来，但是对于指数为n的时候呢？如果n取10万取10亿呢，显然这个代码效率太低了，因为对于一个足够大的n即使是O（n）也是一个很高的复杂度。

二、算法分析　　

　　所以就产生了对于一个数如何快速求出它的幂，这样的问题。

　　基于二分法思想，就可以尝试将指数进行二分，指数足够小，就可以快速求出幂，然后把这些部分幂相乘就得出了结果。

　　所以就产生了对于指数进行二分的想法，下面考虑两种情况

　　设指数j为奇数，则a^j=a*a^j-1。

　　设指数j为偶数，则a^j=(a^j/2)*(a^j/2)。

　　通过上述两种方法就可以得出一个求快速幂的方法，当指数部分为奇数时，可以让指数降一次幂变成偶数，当指数部分为偶数时，就对指数进行二分。

　　这里给出这个代码的一种递归解法

　　

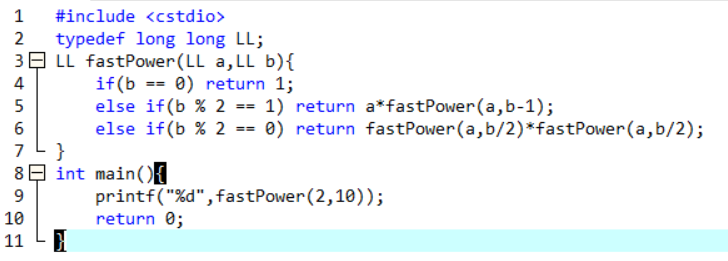
　　注意：递归算法虽然简单，但是递归对于空间的利用是很恐怖的。

三、非递归方法

　　书中对于非递归方式的实现非常巧妙，所以这里直接给出书中思想。

　　对于b来说，可以把b写成2进制的形式，假设b=9，那么二进制的b=1001，那么在把b由二进制转换10进制时可以得到这样一个关系式 b(10)=1*2^3+0*2^2+0*2^1+1*2^0

　　所以这个关系式就是指数的一种变形，我们都知到，指数的加和可以拆分成多项相乘的形式。所以a^b=a^(1*2^3)*a^0*a^0*a^(1*2^0)。

　　只需要分别求出这几项然后乘积就行了

　　具体实现：

　　　　1、开始时定义结果变量ans=1；

　　　　2、判断b的二进制末尾是否为1，如果是则令ans=ans*a

　　　　3、令a=a*a，并且将b右移，（这里相当于计算下一项的值了，因为最低项已经算入ans所以应当过滤掉，可带入上述关系式一起理解）

　　　　4、只要b>0就返回步骤2

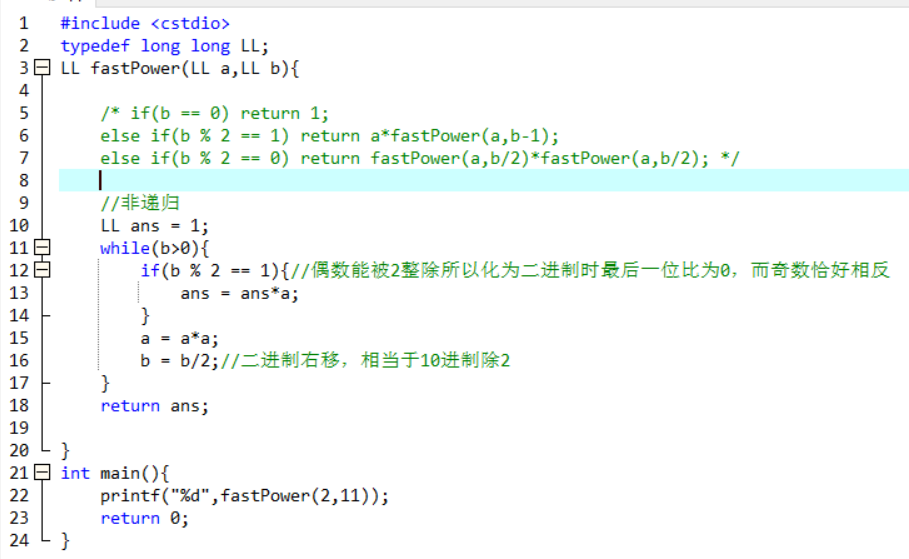
　　代码