算法入门——二分：二分法拓展

二分法拓展

一、引子

　　可以设想一个问题，怎么求？我们日常生活中总是找平方小于2和平方大于2的两个数，那么肯定介于这两个数之间，然后我们让两个数不断逼近，左边加一点，右边减一点，最终我们一定能求得一个近似的结果，其实采用二分法也可以实现求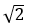这个功能。

 

 

二、算法描述

　　我们可以定义一个区间[1,n]那么的值一定在这个区间中，然后就可以通过对区间的不断压缩找到我们想要的结果。

 

 

　　其实压缩区间的过程，是一种逐步精确的过程，举个例子，假设我们要求2的平方根，首先肯定是确定两个边界1和2，因为1^2<2<2^2；然后我们可以对上界进行压缩取（1+2）/2=1.5，因为1^2<2<1.5^2；那么再次压缩（1+1.5）/2=1.25；因为1.25^2<2<1.5^2，那么就再次压缩（1.25+1.5）/2=1.375，这时候精度已经来到了小数点后三位，然后不断重复下去，结果超过就压缩上界，结果没超过就压缩下界，直到到达我们想要的精度，这时候这个值就无限趋近于，我们就得到了想要的结果

 

 

　　下面给出这个算法的代码

　　

 

 

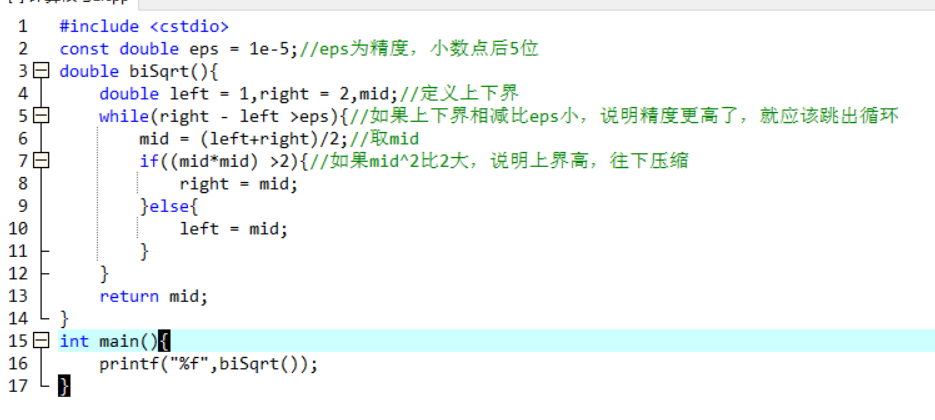
 三、算法拓展

　　其实求根号2只是一种例子，为了使代码泛用性更号应该对代码进行一定优化，那么对于前面问题的分析，其实我们就是在找一个数满足-=0这样的一个一元方程，所以我们可以设有一个一元方程f(x)=0，现在求这个方程的解x，当然这个x是给定范围的一个数

　　所以有了下面的代码

　　

 

 　　这里引入了一个问题就是f(x)的单调性问题，因为已知f（x）的单调性，对于单调增函数如果带入的mid使得函数值偏大，那么说明mid偏大了，对于减函数这个结论应该反过来，也就是说如果减函数的mid使函数值偏大，说明mid偏小了。

 

四、总结

　　综上，对于一个求函数在区间上零点的问题就可以用压缩区间的二分法解得，所以处理此类问题时，可先对问题列出一个关系方程，找出这个方程中的变化量的区间，然后不断对区间压缩，最后就可以确定这个变化量。