leetcode每日一题(2021.5.18)——爬楼梯

题目：爬楼梯

一、题目链接：https://leetcode-cn.com/problems/climbing-stairs/

二、问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

 

三、解题思路

　　拿到题目，可以先在草稿纸上推演一下。

　　方案一：（弃用）

　　　　先尝试n=4时：

　　　　　　　　　1、1+1+1+1

　　　　　　　　　2、1+1+2

　　　　　　　　　3、1+2+1

　　　　　　　　　4、2+1+1

　　　　　　　　　5、2+2

　　　　　　　　总共有5种方法：

　　　　再尝试n=5时:

　　　　　　　　1、1+1+1+1+1

　　　　　　　　2、1+1+1+2

　　　　　　　　3、1+1+2+1

　　　　　　　　4、1+2+1+1

　　　　　　　　5、2+1+1+1

　　　　　　　　6、2+2+1

　　　　　　　　7、2+1+2

　　　　　　　　8、1+2+2

　　　推演的过程中可以发现，n阶楼梯，如果要用最少的步数走完，那么最少的步数是：奇数阶最少n/2+1步走完，偶数阶最少n/2步走完，最多都是n步

　　　所以可以按步数对所有走法分类，比如n=5时，最少5/2+1=3步走完，最多5步走完。那么此时可以按步数分类为5-3+1类，5步走完，4步走完，3步走完，三种情况。

　　　还是对于n=5来说，需要4步走完时，序列里必然有5-4个2，需要3步走完时，序列里必然有5-3个2。所以可以总结到的规律有

　　　　　　1、n个台阶最少n/2+n%2步走完，所以可以将步数分成   n-(n/2+n%2)+1种情况

　　　　　　2、当步数为n-i步时，该步数对应的所有走法中必然有i个2，i从0开始。

　　　其实上面的规律不通过总结也可以找到，因为上台阶时如果需要的步数少1，那么序列里肯定有两个1加和成了2。（少一个1，多一个2）

　　既然每种步数里1和2出现的次数知到了，那么只需要对这个序列进行无序排列组合的统计就行了（因为对于每步中出现的所有1，并不需要在意他们的先后顺序，只不过时有x个1和y个位置有几种占坑的方法而已）

　　算法思想，设计一个循环用于计算每类情况对应的走法数量。循环变量i初值为n，循环条件为i<=(n/2+n%2)，每次循环i-1

　　　　　　　循环过程中当前为i步走完，有n-i个2，计算C_i^n-i，也就是i!/(n-i)!*(2i-n)!，并将结果加到要返回的变量rin上

　　问题：求很大的数的阶乘出现越界，无法用代码实现该算法（弃用）

 

　　方案二：动态规划

　　这个方案是我在看官方解答后了解到的，这是我第一次接触这种算法思想。

　　动态规划的意识大致就是我本次计算的结果要用到上次的结果，还是利用n=4，n=5的例子，如果要求n=6时就是在n=4的基础上跨两阶或者在n=5的基础上跨一阶台阶。因为上到第四阶的所有可能的方法已经得出，接下来如果要只走一步上到第6阶就只能一次跨2阶，在第5阶时也是同理。所以上到第六阶的方案和应该是上到第四阶的方案和加上到第五阶的方案和相加。或者说是在上文列出的n=4的所有式子中都加2，以及在n=5的所有式子中都加1，就是上到第6阶的方案。

　　按照上述思想可以得出一个函数

f(x)=f(x-1)+f(x-2)

　　按照这个函数就可以递推出所有的f(x)了。

　　可以先自己算出f(1)=1和f(2)=2　　

　　下面分析代码：

　　

 

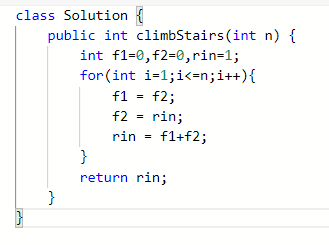
 　　这里官方给出了一个滚动数组的概念，在一个数组中有三个元素{f1,f2,rin}，f1记录函数f(x-1)的结果，f2记录函数f(x-2)的结果，rin就是f(x)的结果。

　　f1，f2初值都赋0，稍后通过滚动更新他们的值，rin初值设为1，表示f(0)的结果，我们要计算f(2)时需要用到f(0)，可以通过方案一的代码求得f(0)=1就是排列组合中的C00，

　　这样就可以开始滚动数组了rin滚动到f2上，f2滚动到f1上此时f2就记录了f(0)的结果，rin上就是f(1)的结果，下次滚动，f1上记录f(0)的结果1；f2上记录了f（1）的结果1，此时可以求得f(2)=1+1，所以rin就等于f1+f2；

四、总结

　　今天第一次了解到动态规划以及滚动数组，这些算法和数据结构对我来说还是很抽象的，这道题包含的算法思想也值得以后再看。