秋招-智力题总结

1、有100个饺子，两个人轮流拿，一次可拿1～5个，问怎么样可以保证是你自己最后拿

答：我一定要抢先拿4个，之后永远是对方拿x个，我拿6-x个，能保证最后是我拿

2、一个岛上有红黄蓝三种颜色的兔子，数量分别为a,b,c，任意两只不同颜色的兔子碰撞变成两只第三种颜色的兔子，a,b,c满足什么样的关系可以使得有可能经过足够长时间的碰撞，岛上最终都是一种颜色的兔子

答：存在两个数模3相等

3、利用烧绳子计算时间

现有若干不均匀的绳子，烧完这根绳子需要一个小时，问如何准确计时15分钟，30分钟，45分钟，75分钟。。。

计算15分钟：对折之后两头烧(要求对折之后绑的够紧，否则看45分钟解法)

计算30分钟：两头烧

计算45分钟：两根，一根两头烧一根一头烧，两头烧完过了30分钟，立即将第二根另一头点燃，到烧完又过15分钟，加起来45分钟

计算75分钟：将30和45分钟的方式加起来就可以了

其余类似

 4、有一个水龙头，一个5L水杯，一个7L水杯，如何精准地获得6L水？

  • 将7L的加满水往5L的里面注满，剩下2L，倒空5L的瓶子，将7L中剩下的2L倒入5L的瓶子中。
  • 将7L的加满水往5L的里面注满，剩下4L，倒空5L的瓶子，将7L中剩下的4L倒入5L的瓶子中。
  • 将7L的加满水往5L的里面注满，剩下6L。

5、有四队参加比赛，两个之间对比，赢一场3分，平一场1分，输一场0分，有一队不被淘汰，最少要得多少分

  • 最少保证7分，要2赢1平才能不被淘汰

6、100层楼，只有2个鸡蛋，想要判断出那一层刚好让鸡蛋碎掉，给出策略

  • 暴力法：从1楼开始，最坏的情况需要100次

  • 二分法：采用类似于二分查找的方法，把鸡蛋从一半楼层（50层）往下扔。如果第一枚鸡蛋，在50层碎了，第二枚鸡蛋，就从第1层开始扔，一层一层增长，一直扔到第49层。如果第一枚鸡蛋在50层没碎了，则继续使用二分法，在剩余楼层的一半（75层）往下扔......这个方法在最坏情况下，需要尝试50次。

  • 均匀法：如何让第一枚鸡蛋和第二枚鸡蛋的尝试次数，尽可能均衡呢？很简单，做一个平方根运算，100的平方根是10。因此，我们尝试每10层扔一次，第一次从10层扔，第二次从20层扔，第三次从30层......一直扔到100层。这样的最好情况是在第10层碎掉，尝试次数为 1 + 9 = 10次。最坏的情况是在第100层碎掉，尝试次数为 10 + 9 = 19次。不过，这里有一个小小的优化点，我们可以从15层开始扔，接下来从25层、35层扔......一直到95层。这样最坏情况是在第95层碎掉，尝试次数为 9 + 9 = 18次。

7、 有1000个一模一样的瓶子，其中有999瓶是普通的水，有1瓶是毒药。任何喝下毒药的生命都会在一星期之后死亡。现在你只有10只小白鼠和1个星期的时间，如何检验出哪个瓶子有毒药？

  • 首先一共有1000瓶，2的10次方是1024，刚好大于1000，也就是说，1000瓶药品可以使用10位二进制数就可以表示。从第一个开始：

    第一瓶 ： 00 0000 0001

    第二瓶： 00 0000 0010

    第三瓶： 00 0000 0011

    ……

    第999瓶： 11 1111 0010

    第1000瓶： 11 1111 0011

    需要十只老鼠，如果按顺序编号，ABCDEFGHIJ分别代表从低位到高位每一个位。 每只老鼠对应一个二进制位，如果该位上的数字为1，则给老鼠喝瓶里的药。观察，若死亡的老鼠编号为：ACFGJ，一共死去五只老鼠，则对应的编号为 10 0110 0101，则有毒的药品为该编号的药品，转为十进制数为：613号。（这才是正解，当然前提是老鼠还没被撑死）

8、博弈论问题

9、 瓶子换饮料问题：1000瓶饮料，3个空瓶子能够换1瓶饮料，问最多能喝几瓶？

  • 拿走3瓶，换回1瓶，相当于减少2瓶。但是最后剩下4瓶的时候例外，这时只能换1瓶。所以我们计算1000减2能减多少次，直到剩下4.（1000-4=996，996/2=498）所以1000减2能减498次直到剩下4瓶，最后剩下的4瓶还可以换一瓶，所以总共是1000+498+1=1499瓶。

10、放n只蚂蚁在一条树枝上，蚂蚁与蚂蚁之间碰到就各自往反方向走，问总距离或者时间

  • 碰到就当没发生，继续走，相当于碰到的两个蚂蚁交换了一下身体。其实就是每个蚂蚁从当前位置一直走直到停止的总距离或者时间。

11、有25匹马，每场比赛只能赛5匹，至少要赛多少场才能找到最快的3匹马？

  • 第一次，分成5个赛道ABCDE，每个赛道5匹马，每个赛道比赛一场，每个赛道的第12345名记为 A1,A2,A3,A4,A5 B1,B2,B3,B4,B5等等，这一步要赛5场。
  • 第二次，我们将每个赛道的前三名，共15匹。分成三组，然后每组进行比赛。这一步要赛3场。
  • 第三次，我们取每组的前三名。共9匹，第一名赛道的马编号为1a,1b,1c，第二名赛道的马编号为2a,2b,2c，第三名赛道的马编号为3a,3b,3c。这时进行分析，1a表示第一名里面的第一名，绝对是所有马中的第一，所以不用再比了。2c表示第二名的三匹里头的最后一匹，3b和3c表示第三名里面的倒数两匹，不可能是所有马里面的前三名，所以也直接排除，剩下1b,1c,2a,2b,,3a，共5匹，再赛跑一次取第一第二名，加上刚筛选出来的1a就是所有马里面的最快3匹了。这一步要赛1场。
  • 所以一共是5+3+1=9场。

12、在24小时里面时针分针秒针可以重合几次

  • 24小时中时针走2圈，而分针走24圈，时针和分针重合24-2=22次，而只要时针和分针重合，秒针一定有机会重合，所以总共重合22次

13、1000个苹果10个箱子，如何把这1000个苹果装在这10个箱子里，才能使不管任何数量（1-1000）的苹果，都能一次给出？

  • 1000个苹果，最接近1024，转化为2进制，需要占用10个bit，则从右往左数，第一个bit位表示1个苹果，第二个bit位表示2个苹果，第三个bit位表示4个苹果，，，第10个bit位表示剩下的489个苹果。分别把这些通过放入相同编号的箱子里。当需要某一数量的苹果时，查看这些数量的哪些bit位为1，为1则表示这个bit位代表有苹果，取出对应编号的箱子即可。

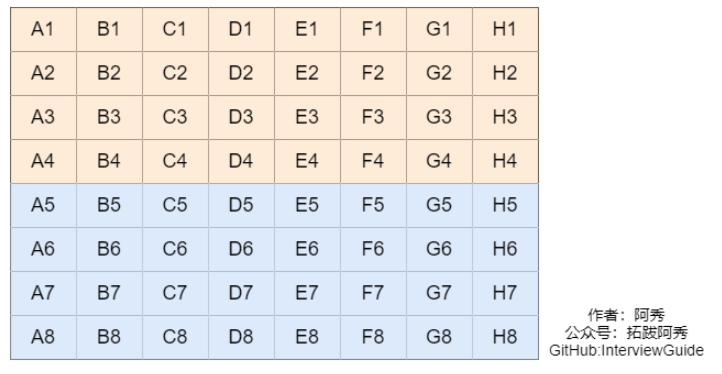
14、64匹马8条跑道找最快的4匹马，需要跑几次？

  • 第一步 全部马分为8组，每组8匹，每组各跑一次，然后淘汰掉每组的后四名，如下图（需要比赛8场）

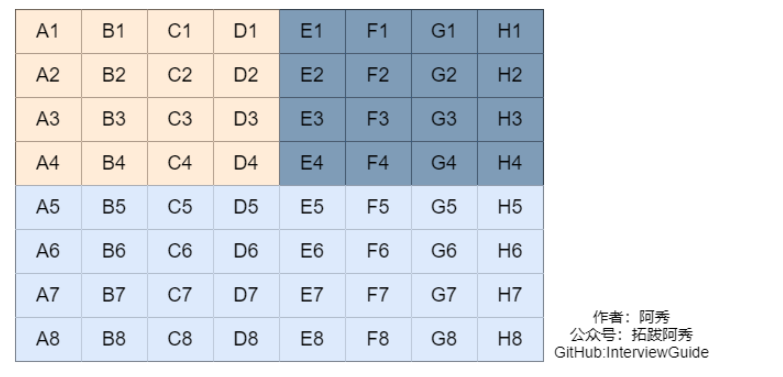
  • 第二步 取每组第一名进行一次比赛，然后淘汰最后四名所在组的所有马，如下图（需要比赛1场） 

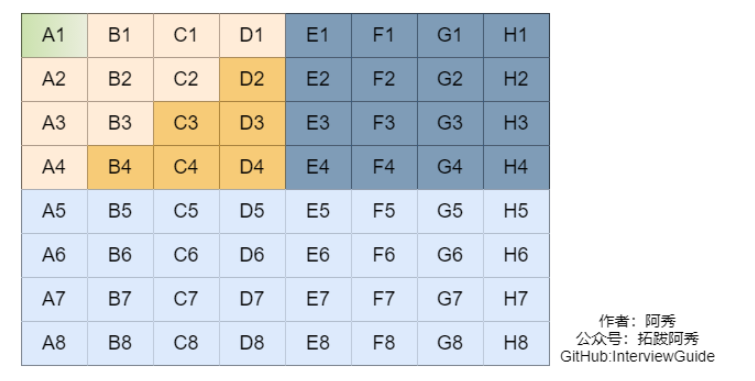
  • 这个时候总冠军已经诞生，它就是A1，蓝域（它不需要比赛了）。而其他可能跑得最快的三匹马只可能是下图中的黄域了（A2,A3,A4,B1,B2,B3,C1,C2,D1，共9匹马） 

  • 第三步 只要从上面的9匹马中找出跑得最快的三匹马就可以了，但是现在只要8个跑道，怎么办？那就随机选出8匹马进行一次比赛吧（需要比赛一场） 

  • 第四步 上面比赛完，选出了前三名，但是9匹马中还有一匹马没跑呢，它可能是一个潜力股啊，那就和前三名比一比吧，这四匹马比一场，选出前三名。最后加上总冠军，跑得最快的四匹马诞生了！！！（需要一场比赛）
  • 最后，一共需要比赛的场次：8 + 1 + 1 + 1 = 11 场

15、1元一瓶饮料2个空瓶可以换一瓶饮料，你有20元钱，问你最多能喝多少瓶？

  • 20+10+5+2+1+1=39；前面的都不用说，到35之后；还有5个瓶子，换两瓶，剩下3个瓶子，接着再换一个，剩两个瓶子，再换一瓶，加起来为35+2+1+1=39。
posted @ 2021-09-21 18:49  Z9Y1J5  阅读(976)  评论(0)    收藏  举报