EDA 中的 DRC 检测—— multiple pattern 技术和对应 drc 检测

multiple pattern

多重图案光刻（MPL，MultiplePatternLithography）是在当前光刻技术下制造更小特征尺寸和更小间距的版图的方法。多重图案光刻包含适用于 22m 和 16nm 工艺的双重图案光刻（DPL，DoublePatternLithography）和适用于 7nm 和 5nm 工艺的三重图案光刻（TPL，TriplePatternLithography），及更多重光刻技术。

MPL 技术的工艺流程如图3所示，在满足间距规则的前提下，将初始版图的图案分配到多层掩模进行制造。MPL版图分解算法的关键是合理地将不同图案分配到不同掩模层，一般抽象为着色问题，有如下两个评估指标：（1)分解速度，即掩模层分配方案的求解速度要快；（2）分解质量，即分配完成后存在的冲突边和缝合边数目要少。

为了优化分解速度，Kuang 提出了图匹配查找表法，可以加速版图着色，但只适用小规模版图。X.Li 提出离散松弛方法求解TPL，对于小规模版图求解质量好，速度快，但同样对于大规模版图求解速度慢。Yu 提出整数线性规划（ILP，IntegerLinearProgram)及半正定规划（SDP，SemidefiniteProgram）加速解决 TPL 问题，求解质量高，但是求解速度慢，加速效果有限。Jiang将MPL问题构建为精确覆盖问题，并采用舞蹈链算法进行求解，求解速度很快，但内存消耗过大。

奇数环和奇数轮

以两种和三种 mask 的处理为例，在 drc 检测中为了保证每层的 metal wire 都可以拆分成两个 mask，通常通过奇数环的方式检测（odd loop）；而为了检测三种 mask 造成的掩模冲突，则通过奇数轮的方式（odd cycle）。

2个mask——奇数环

当可以拆分成两个 mask 时，我们考虑的图形是奇数环。

图1

如上图所示，三个蓝色 cut 可以构成一个奇数环，三个蓝色 cut 加上另外三个 cut 中的任意一个即是一个偶数环，而三个蓝色 cut 加上另外三个 cut 中的任意两个可以构成一个奇数环，三个蓝色 cut 加上另外三个 cut 即是一个偶数环。当存在 2个 mask 时，奇数环总是会出现 drc violation 的，而偶数环不会。

3个mask——奇数轮

当拆分成三个 mask 时，我们考虑两种图形：奇数星型图和偶数星型图（有一个中心节点的环），或者统称为奇数轮。

图2

如图2所示，可以将图2分为两个部分，一个是中间的紫色 cut，另一个则是除了紫色 cut 之外的其他所有 cut。假设紫色 cut 占据了三个 mask 中的一个 mask，则问题回到了判断 2个 mask 的情况，可以沿用上面的结论。基于奇数环和奇数轮的检测，基本可以覆盖常见的 same mask 检测。

图划分算法

graph partion 主要有两种场景，点分割 vertex partion 和边分割 edge partition。

点分割是将原来图中所有的点划分导不同集合中，不同集合中的点不重合，同时尽可能最大化或者最小化某些目标函数。如下图右上，需要删除原先的某些边（Edge cut）。

边分割就是将原来图中的所有边划分到不同集合中，不同集合中的边不重合，同时尽可能最大化或者最小化某些目标函数。如下图右下，会出现节点的重复，好像节点被切割成了多个（Vertex cut），因为原先的某个节点可能会出现在多个集合中。

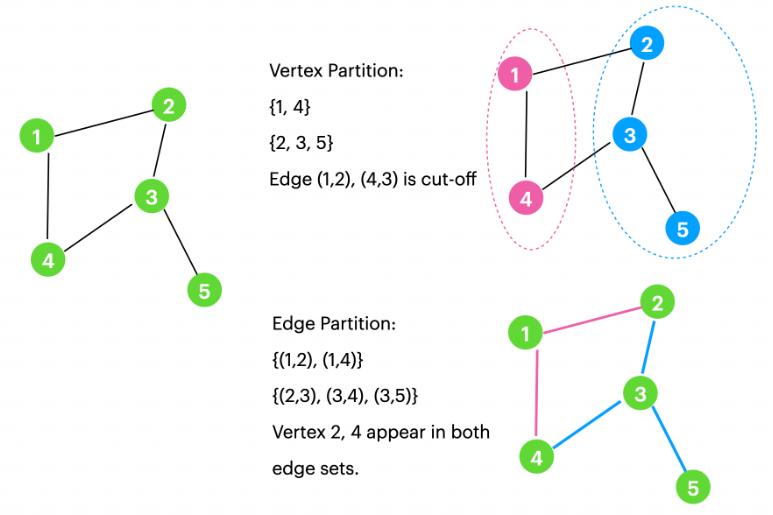
对于存在 n 个mask的掩模冲突，可以看作约束条件下的图划分问题，如果采用点分割，即是将所有通孔划分到 n 个点集合中。