因果推断学习笔记01.Yule-Simpson悖论

Yule-Simpson悖论是统计学上一个很经典的例子，他揭示了以相关性为基础的传统统计学的根本问题——不能很好的解释因果性，同时也促进了因果推断方法的发展。我第一次接触Yule-Simpson悖论是在袁卫老师《统计学概论》的课上，当时大一的我十分困惑，并没有理解这个悖论的本质。

作为因果推断学习笔记的第一篇内容，本文主要参考了丁鹏老师的A First Course in Causal Inference第一章以及他发表在统计之都上的因果推断简介之一：从 Yule-Simpson’s Paradox 讲起，希望从不同的角度解释清楚Yule-Simpson悖论。

一个二值变量的例子

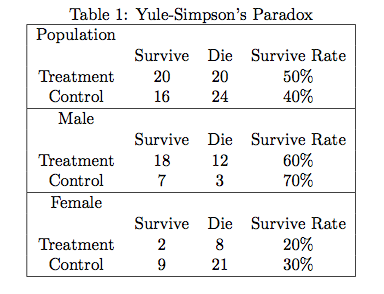
上表展示了某种药物实验中，处理组和对照组中，男性和女性各自的存活率以及总体的存活率。从总体来看，处理组的存活率为50%，对照组的存活率为40%，说明该种药物是有效的。

然而分别观察男性和女性的数据，对照组的存活率均高于处理组，这就产生了矛盾：这种药物对男性和女性都有负作用，居然对总体却有正作用！

用统计语言来说，如果令X表示是否处理，Y表示是否死亡，Z表示性别，且：

\[X=\left\{ \begin{array}{**lr**} 1,处理\\0,对照 \end{array} \right. \quad Y=\left\{ \begin{array}{**lr**} 1,死亡\\0,存活 \end{array} \right. \quad Z=\left\{ \begin{array}{**lr**} 1,女性\\0,男性 \end{array} \right. \]

则X和Y的相关系数小于0，但是给定变量Z，\(Cov(X,Y|Z)>0.\)这说明，相关性不能用于描述因果关系。

一个正态变量的例子

Yule-Simpson悖论不仅在二项分布中存在，下面举一个正态分布的例子，假设

\[\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right) \sim \mathrm{N}\left(\left(\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right),\left(\begin{array}{ccc} 1 & \rho_{X Y} & \rho_{X Z} \\ \rho_{X Y} & 1 & \rho_{Y Z} \\ \rho_{X Z} & \rho_{Y Z} & 1 \end{array}\right)\right) \]

我们的目标是使得\(Cov(X,Y)<0,Cov(X,Y|Z)>0\)（注意保持协方差矩阵的正定），可以得到一个解\(\rho_{XY}=-0.5,\rho_{YZ}=0.8,\rho_{XZ}=-0.8.\)

解释与启发

在二值变量的例子中，从数学的角度很容易解释，即：

\[\frac{a}{b}<\frac{c}{d}, \frac{a^{\prime}}{b^{\prime}}<\frac{c^{\prime}}{d^{\prime}}, \frac{a+a^{\prime}}{b+b}>\frac{c+c^{\prime}}{d+d^{\prime}} \]

但是他在统计上有着很重要的意义。注意，悖论出现并不是因为数据的随机性或者分布的特殊性，它是普遍存在的，且表明相关性不等于因果性。因此，很多人认为不能用统计的方法研究因果性。

然而，我们还是可以从以上两个例子中得到一些启发。在正态变量的例子中，有\(Cov(X,Y|Z)=\rho_{XY}-\rho_{XZ}\rho_{YZ}\)，如果令\(\rho_{XZ}=0\)（等价于二者独立），那么两个相关系数就不会出现异号的情况，回到第一个例子，也就是处理组和对照组的分配与性别独立时，Yule-Simpson悖论就不会出现。

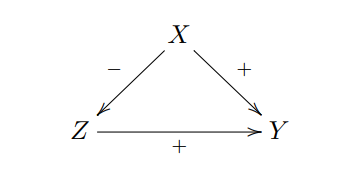
我们同样可以通过图的形式给出解释，X通过两条途径影响Y，一方面X对Y有正面作用，另一方面X对Z有负面作用，Z对Y有正面作用，即在男性和女性当中，更倾向于男性接受处理，而男性的死亡率比女性更低。最终，X对Y的总影响是负面的，而固定Z，X对Y的影响是正面的，这样就很好的解释了Yule-Simpson悖论。同样，如果使得X和Z独立，切断二者之间的因果作用，就可以避免悖论的产生。

因此，实验的分配机制变得尤为重要。在精心设计的实验中，我们也许可以通过切断XZ边的方法发现因果关系。当然，如果实验结果（是否死亡）仅受到我们关心的因素（是否处理）的影响而不受其他因素（性别）的影响（也就是Y,Z之间没有边），则实验结果也是可信的，但是在真实世界中，这是不可能的。我们将影响实验结果但不关心的因素称为混杂(confoundness)，因此分配机制的重要性也可以理解为控制混杂因素的重要性。

在很多领域的研究中，我们无法通过设计实验的方式获取数据，而只能进行观察性研究，所以因素的混杂不可避免，这在经济学上被称为“内生性问题”。比如说吸烟对癌症的关系，究竟是吸烟导致的癌症，还是吸烟和癌症受相同基因表达的影响？这样的问题是很难回答的。统计学家的工作，正是发展出一套严格的数学工具描述这样的问题，并在一些很强的假设下尝试做出解答。