机器学习：异常检测(概率密度)

一、异常检测(Anomaly Detection)

识别数据中异常的数据点

 任务一:根据设备上传感器1与2的数据自动监测设备异常工作状态

其中：sensor就是传感器的意思。

 任务二:自动寻找图片中异常的目标

更多案例:

（1）、异常消费检测(商业)

（2）、劣质产品检测(工业)

（3）、缺陷基因检测(医疗)。。。

异常检测的定义：根据输入数据，对不符合预期模式的数据进行识别。

一维数据集 ：{x⁽¹⁾,x⁽²⁾,..x^(m)}

 一维数据找异常点的方式：寻找低概率数据（事件）

概率密度：概率密度函数是一个描述随机变量在某个确定的取值点附近的可能性(即概率)的函数。

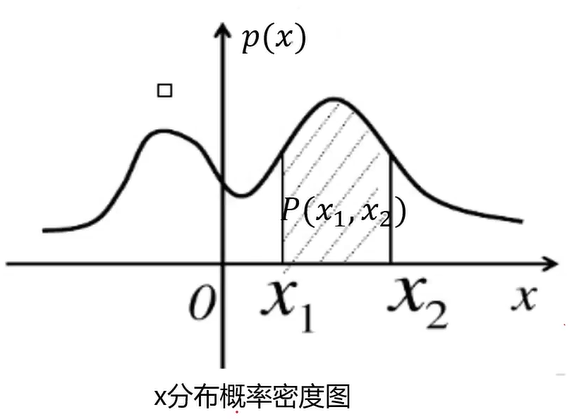
区间(x1,x2)的概率为:

高斯分布（即正态分布）的概率密度函数是:

 其中，u为数据均值，σ为标准差

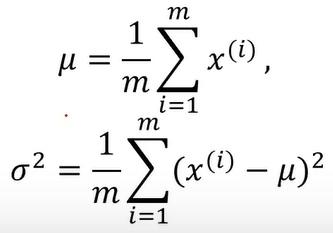
计算均值与标准差的示例：

均值：u=1/4(-1+0+1+2)=0.5

标准差：σ²= 1/4[(-1-0.5)² + (0-0.5)² + (1-0.5)²  + (2-0.5)² ] = 1.2

基于高斯分布实现异常检测：

　　1、计算数据均值μ，标准差σ

　　2、计算对应的高斯分布概率函数p(x)

　　3、根据数据点概率，进行判断。如果p(x)< ε:则该点为异常点

当数据维度高于一维怎么办?nxm

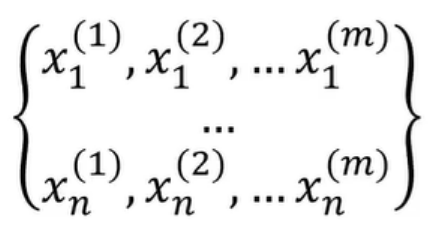
（1）、计算数据均值μ₁,μ₂.……μ_n,,标准差σ₁，σ₂.….,σ_n

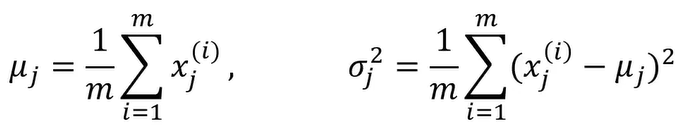
x1(1),x1(2),...,x1(m)的均值为μ_1，标准差为σ₁

（2）、计算概率密度函数p(x)

∏表示连乘，j从1到n将不同维度的概率密度p(x₁),p(x₂),...,p(x_n)相乘

举例：计算二维数据x₁和x₂的概率密度

已知：u1= 3,σ1 = 0.5，u2=4,σ2= 0.14，ε=0.05,判断x₁= 3.5,x₂= 3.5是不是异常点。

计算过程如下:

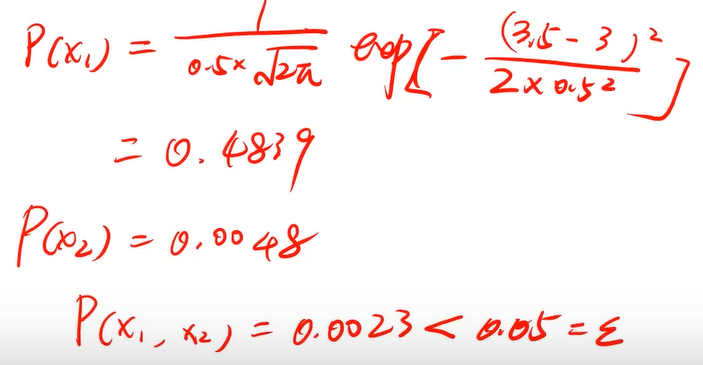
所以x₁= 3.5,x₂= 3.5是异常点。

概率密度函数三维图像如下：

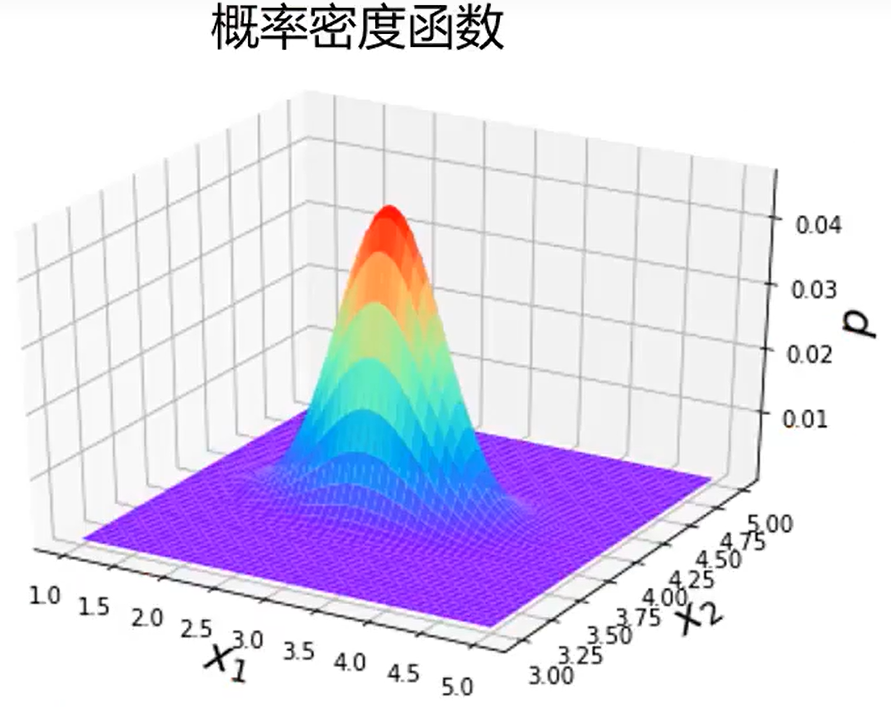
二、实战(二)-异常数据检测

1、基于 anomaly_data.csv数据，可视化数据分布情况、及其对应高斯分布的概率密度函数

2、建立模型，实现异常数据点预测

3、可视化异常检测处理结果

4、修改概率分布阈值contamination（默认contamination=0.1)，查看值改变对结果的影响

数据集anomaly_data.csv免费下载：

通过网盘分享的文件：anomaly_data.csv
链接: https://pan.baidu.com/s/16pRCfbogvW_iHEXNzIv13A 提取码: v554 
--来自百度网盘超级会员v6的分享

1、数据加载

import torch
import pandas as pd
import numpy as np
# from matplotlib import pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
#加载数据
data = pd.read_csv('./data/anomaly_data.csv')
print(data)

结果:

            x1         x2
0     8.046815   9.741152
1     8.408520   8.763270
2     9.195915  10.853181
3     9.914701  11.174260
4     8.576700   9.042849
..         ...        ...
302   7.476629   9.459370
303  14.582573   5.411619
304  18.339868  11.298874
305  13.261188  12.978309
306  -0.247387  19.350407

2、可视化

# 数据可视化
fig1 = plt.figure(figsize=(10, 7))
plt.scatter(data.loc[:, 'x1'], data.loc[:, 'x2'])
plt.title("data")
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

结果：

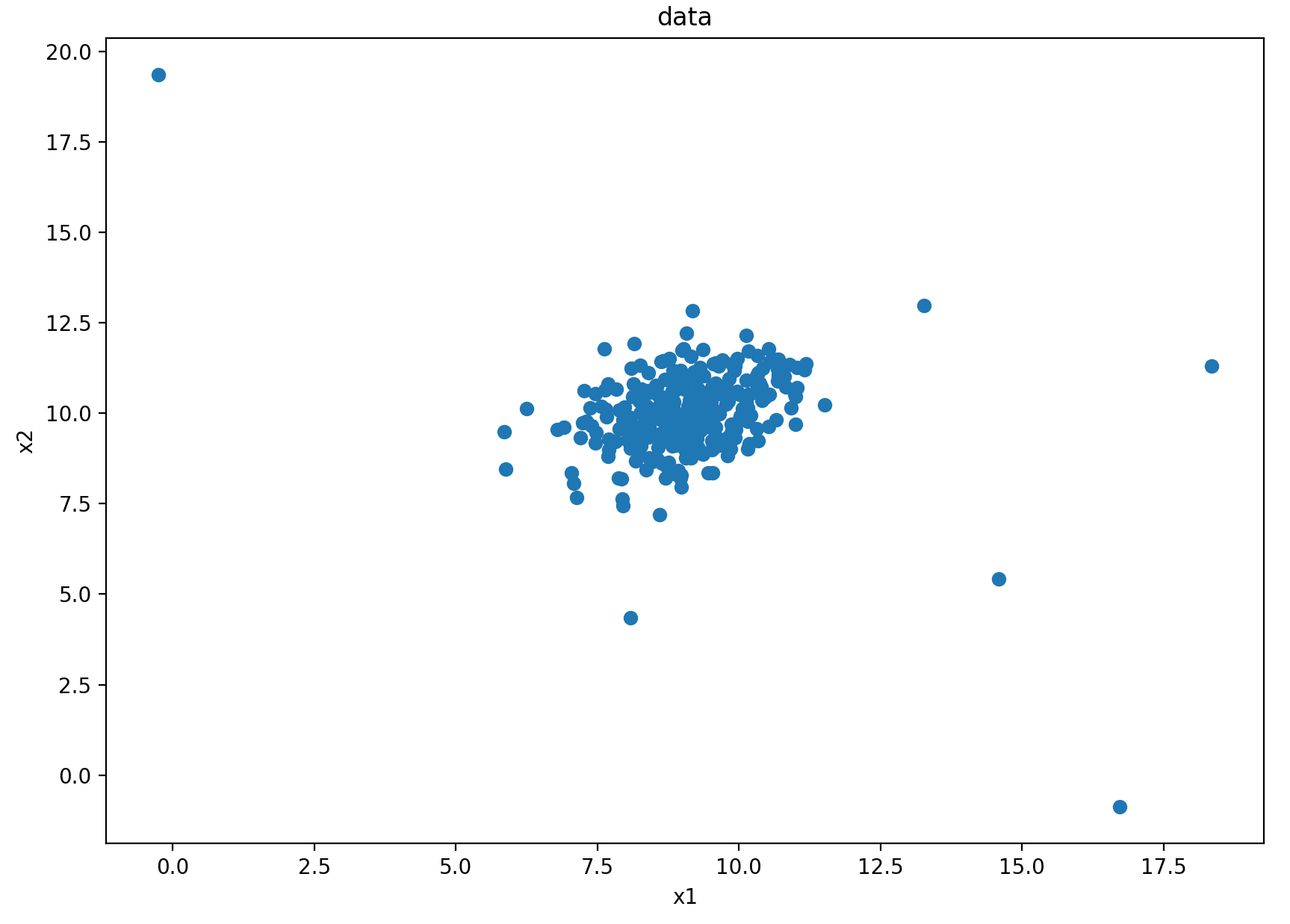
3、定义x1和x2

#define x1 and x2
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']

4、将x1和x2数据分布进行一个可视化

# 将数据分布进行一个可视化
import matplotlib as mlp

font2 = {'family': 'SimHei', 'weight': 'normal', 'size': '20'}  # 定义一下字体（根据自己喜好定义即可）
mlp.rcParams['font.family'] = 'SimHei'  # 设置字体
mlp.rcParams['axes.unicode_minus'] = False  # 字符显示
fig2 = plt.figure(figsize=(20, 7))
plt.subplot(121) #一行两列中的第一列
plt.hist(x1, bins=100)  # 分成100个数据分隔，即有100条条状图
plt.title('x1 数据分布统计', font2)
plt.xlabel('x1', font2)
plt.ylabel('出现次数', font2)
plt.subplot(122) # 一行两列中的第二列
plt.hist(x2, bins=100)  # 分成100个数据分隔
plt.title('x2 数据分布统计', font2)
plt.xlabel('x2', font2)
plt.ylabel('出现次数', font2)
plt.show()

其中plt.hist表示绘制直方图。

结果：

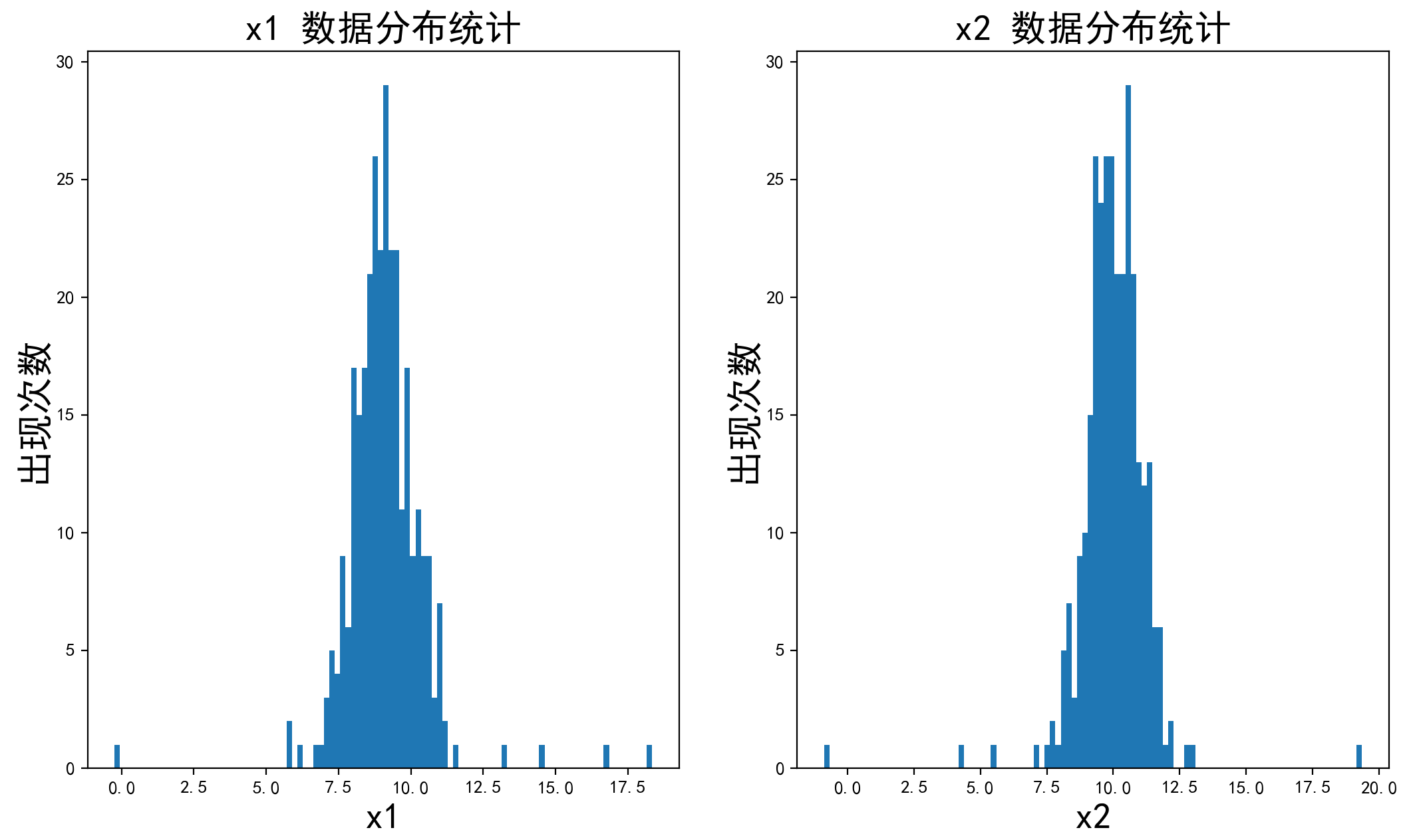下

其中y轴为每个分隔范围x1或x2出现的次数

 5、计算x1、x2的均值(mean)和标准差(sigma)

# 计算x1、x2的均值(mean)和标准差(sigma,即σ)
x1_mean = x1.mean()
x1_sigma = x1.std()
x2_mean = x2.mean()
x2_sigma = x2.std()
print(x1_mean, x1_sigma, x2_mean, x2_sigma)

结果：

9.112225783931596 1.3559573758220915 9.997710507954398 1.3097071175386399

6、计算高斯分布（即正态分布）概率密度函数

由图中可知，x1和x2的范围大致在[0,20]

# 计算高斯分布概率密度函数
from scipy.stats import norm

x1_range = np.linspace(0, 20, 300)  # 范围是0到20，300个点均分
x1_normal = norm.pdf(x1_range, x1_mean, x1_sigma)  # 计算高斯分布概率密度函数
x2_range = np.linspace(0, 20, 300)
x2_normal = norm.pdf(x2_range, x2_mean, x2_sigma)

7、可视化高斯分布概率密度函数

# 可视化高斯分布概率密度函数
fig3 = plt.figure(figsize=(20, 7))
plt.subplot(121)
plt.plot(x1_range, x1_normal)
plt.title('normal p(x1)')
plt.subplot(122)
plt.plot(x2_range, x2_normal)
plt.title('normal p(x2)')
plt.show()

x1_normal为一维数组，类型为ndarray

结果：

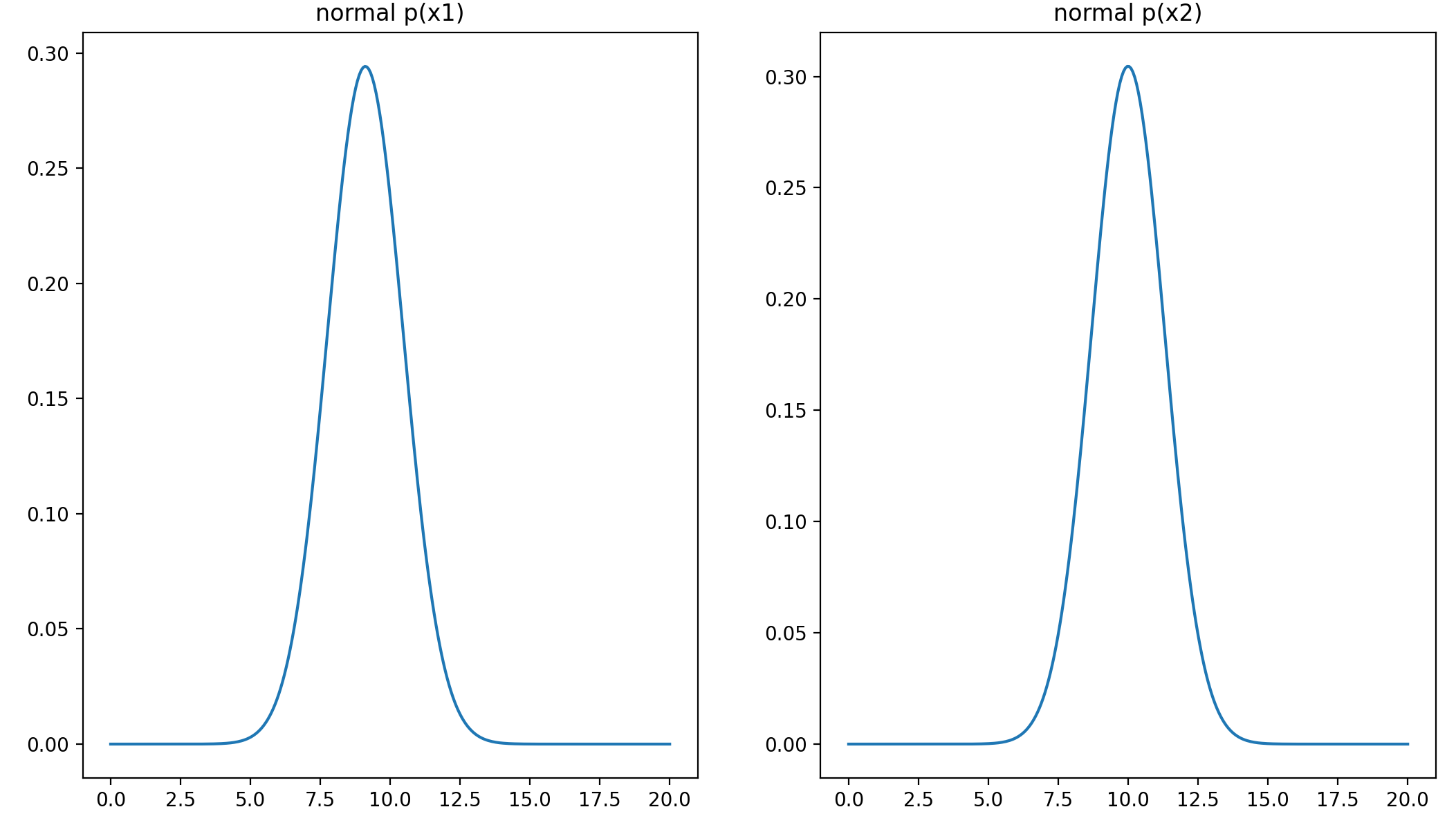
至此，我们任务的第一部分就完成了，下面开始建立模型

8、建立模型

协方差EllipticEnvelope：数据分布中存在异常值是常见的情况。许多算法都能处理异常值，EllipticEnvelope 是 Sklearn 内置的一个优秀示例。该算法在检测正态分布（高斯）特征中的异常值方面表现出色。

#建立模型
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope()
ad_model.fit(data)

9、预测

#预测
y_predict = ad_model.predict(data)
print(pd.Series(y_predict).value_counts())

结果:

 1    276
-1     31
Name: count, dtype: int64

只有两类：1和-1，1表示正常点，-1表示异常点。可以看到异常点占比10%左右，contamination中文表示污染。任务第二步也完成了，然后下一步可视化结果

10、最终结果可视化

# 可视化结果
font2 = {'family': 'SimHei', 'weight': 'normal', 'size': '20'}  # 定义一下字体（根据自己喜好定义即可）
fig4 = plt.figure(figsize=(10, 6))
orginal_data = plt.scatter(data.loc[:, 'x1'], data.loc[:, 'x2'], marker='x')  # 将原始数据各点用'x'表示
anomaly_data = plt.scatter(data.loc[:, 'x1'][y_predict == -1], data.loc[:, 'x2'][y_predict == -1], marker='o',
                           facecolor='none', edgecolor='red', s=150) 
# y_predict==-1即是异常点; marker='o'将异常点用圆圈圈起来; facecolor='none' 不填充，即空心圆; edgecolor='red' 颜色为红色; s=150 圆圈的大小.
plt.title('自动寻找异常数据', font2)
plt.xlabel('x1', font2)
plt.ylabel('x2', font2)
plt.legend((orginal_data, anomaly_data), ('原数据', '检测异常点'))
plt.show()

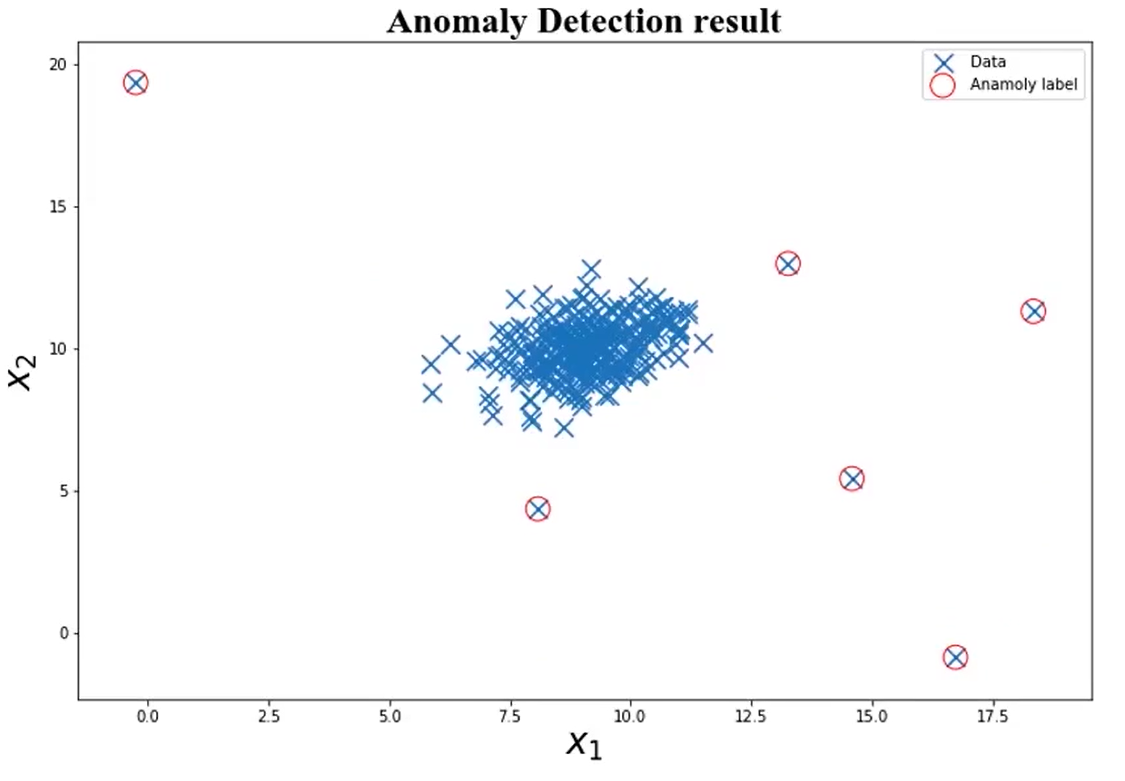
结果：

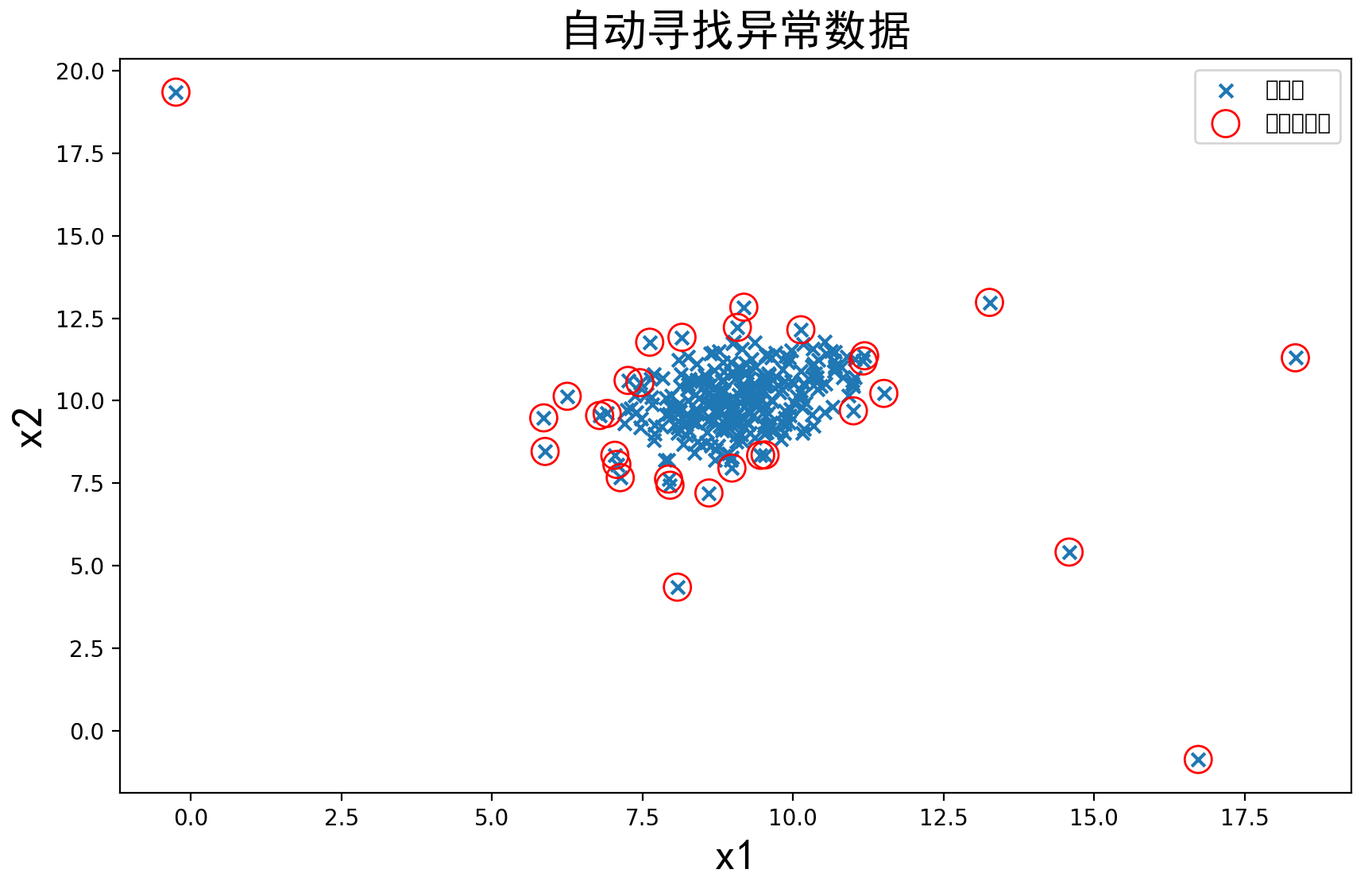
可以看到有些我们感觉是正常数据的点也被标记为异常点了，这时我们可以执行任务的最后一步，修改一下阈值EllipticEnvelope(contamination=0.1)中的contamination，查看阈值改变对结果的影响

#建立模型
from sklearn.covariance import EllipticEnvelope
# ad_model = EllipticEnvelope()
#将contamination的值改为0.03，默认值为0.1
ad_model = EllipticEnvelope(contamination=0.03)
ad_model.fit(data)

结果如下:

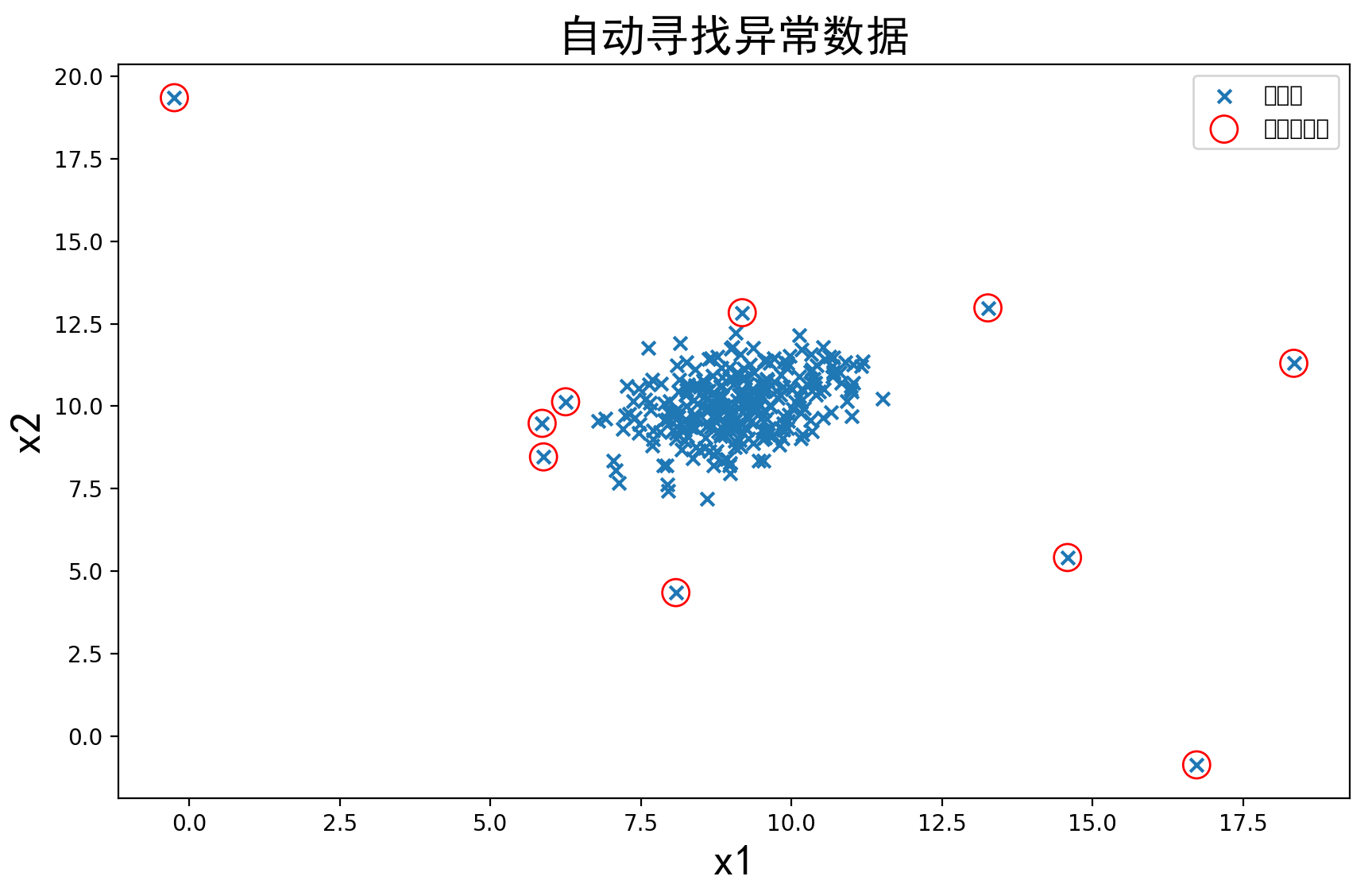
和之前对比可以看出，修改后的结果明显更好。当然，也可以试着改变其他参数的值来达到更好的效果

完整代码：

import torch
import pandas as pd
import numpy as np
# from matplotlib import pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
#加载数据
data = pd.read_csv('./data/anomaly_data.csv')
print(data)

#define x1 and x2
x1 = data.loc[:,'x1']
x2 = data.loc[:,'x2']

# 计算x1、x2的均值(mean)和标准差(sigma)
x1_mean = x1.mean()
x1_sigma = x1.std()
x2_mean = x2.mean()
x2_sigma = x2.std()
print(x1_mean, x1_sigma, x2_mean, x2_sigma)

# 计算高斯分布概率密度函数
from scipy.stats import norm

x1_range = np.linspace(0, 20, 300)  # 范围是0到20，300个点均分
x1_normal = norm.pdf(x1_range, x1_mean, x1_sigma)  # 计算高斯分布概率密度函数
x2_range = np.linspace(0, 20, 300)
x2_normal = norm.pdf(x2_range, x2_mean, x2_sigma)

# # 可视化高斯分布概率密度函数
# fig3 = plt.figure(figsize=(20, 7))
# plt.subplot(121)
# plt.plot(x1_range, x1_normal)
# plt.title('normal p(x1)')
# plt.subplot(122)
# plt.plot(x2_range, x2_normal)
# plt.title('normal p(x2)')
# plt.show()

#建立模型
from sklearn.covariance import EllipticEnvelope
# ad_model = EllipticEnvelope()
#将contamination的值改为0.03，默认值为0.1
ad_model = EllipticEnvelope(contamination=0.03)
ad_model.fit(data)

#预测
y_predict = ad_model.predict(data)
print(pd.Series(y_predict).value_counts())

# 可视化结果
font2 = {'family': 'SimHei', 'weight': 'normal', 'size': '20'}  # 定义一下字体（根据自己喜好定义即可）
fig4 = plt.figure(figsize=(10, 6))
orginal_data = plt.scatter(data.loc[:, 'x1'], data.loc[:, 'x2'], marker='x')  # 将各点用'x'表示
anomaly_data = plt.scatter(data.loc[:, 'x1'][y_predict == -1], data.loc[:, 'x2'][y_predict == -1], marker='o',
                           facecolor='none', edgecolor='red', s=150)
# y_predict==-1即是异常点; marker='o'将异常点用圆圈圈起来; facecolor='none' 不填充，即空心圆; edgecolor='red' 颜色为红色; s=150 圆圈的大小.
plt.title('自动寻找异常数据', font2)
plt.xlabel('x1', font2)
plt.ylabel('x2', font2)
plt.legend((orginal_data, anomaly_data), ('原数据', '检测异常点'))
plt.show()

# 将数据分布进行一个可视化
# import matplotlib as mlp
#
# font2 = {'family': 'SimHei', 'weight': 'normal', 'size': '20'}  # 定义一下字体（根据自己喜好定义即可）
# mlp.rcParams['font.family'] = 'SimHei'  # 设置字体
# mlp.rcParams['axes.unicode_minus'] = False  # 字符显示
# fig2 = plt.figure(figsize=(20, 7))
# plt.subplot(121)
# plt.hist(x1, bins=100)  # 分成100个数据分隔，即有100条条状图
# plt.title('x1 数据分布统计', font2)
# plt.xlabel('x1', font2)
# plt.ylabel('出现次数', font2)
# plt.subplot(122)
# plt.hist(x2, bins=100)  # 分成100个数据分隔
# plt.title('x2 数据分布统计', font2)
# plt.xlabel('x2', font2)
# plt.ylabel('出现次数', font2)
# plt.show()

# 数据可视化
# fig1 = plt.figure(figsize=(10, 7))
# plt.scatter(data.loc[:, 'x1'], data.loc[:, 'x2'])
# plt.title("data")
# plt.xlabel('x1')
# plt.ylabel('x2')
# plt.show()