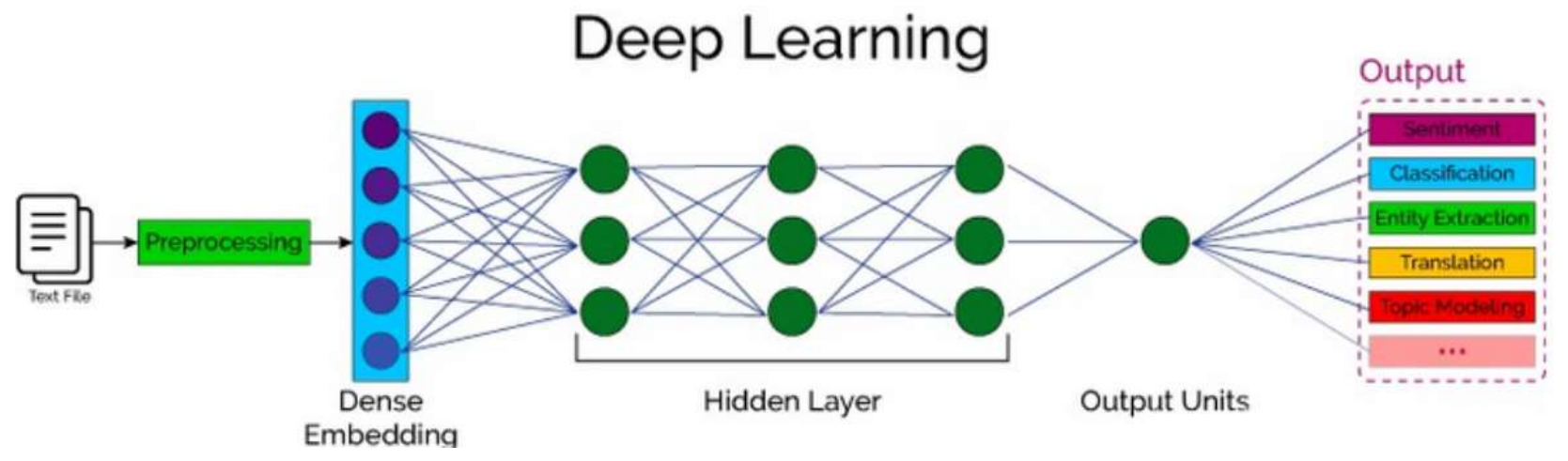
一、自然语言处理NLP概述
二、词嵌入层
词嵌入层的作用就是将文本转换为向量（文本先转索引，索引再向量化，这样词就可以用向量来表示）。
词嵌入层首先会根据输入的词的数量构建一个词向量矩阵，例如: 我们有 100 个词，每个词希望转换成 128 维度的向量，那么构建的矩阵形状即为: 100*128（100行128列，即每一行代表一个词），输入的每个词都对应了一个该矩阵中的一个向量。
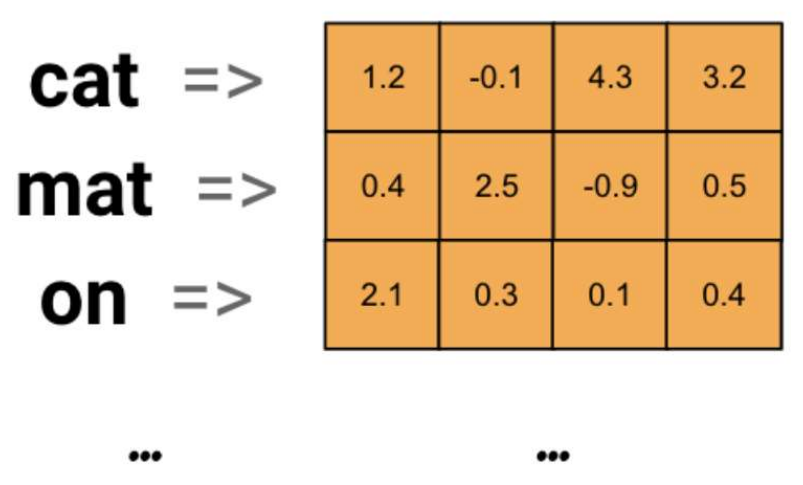
在 PyTorch 中，使用 nn.Embedding 词嵌入层来实现输入词的向量化。
nn.Embedding(num_embeddings=10, embedding_dim=4)
nn.Embedding 对象构建时，最主要有两个参数:
1. num_embeddings 表示词的数量
2. embedding_dim 表示用多少维的向量来表示每个词
接下来，我们将会学习如何将词转换为词向量，其步骤如下:
1. 先将语料进行分词，构建词与索引的映射，我们可以把这个映射叫做词表，词表中每个词都对应了一个唯一的索引
2. 然后使用 nn.Embedding 构建词嵌入矩阵，词索引对应的向量即为该词对应的数值化后的向量表示。
例如，我们的文本数据为: "北京冬奥的进度条已经过半，不少外国运动员在完成自己的比赛后踏上归途。" ，
import torch import torch.nn as nn import jieba if __name__ == '__main__': # 0.文本数据 text = '北京冬奥的进度条已经过半，不少外国运动员在完成自己的比赛后踏上归途。' # 1. 文本分词 words = jieba.lcut(text) print('文本分词:', words) # 2.分词去重并保留原来的顺序获取所有的词语 unique_words = list(set(words)) # 使用set去重无法表示数据的序列关系，这里通过list就构建了词与索引的映射 print("去重后词的个数:\n",len(unique_words)) # 3. 构建词嵌入层:num_embeddings: 表示词的总数量;embedding_dim: 表示词嵌入的维度 embed = nn.Embedding(num_embeddings=len(unique_words), embedding_dim=4) print("词嵌入的结果：\n",embed) # embed可以看作是18行4列的矩阵， # 4. 词语的词向量表示（根据词的索引查找这个索引对应的行来获取该词的向量） for i, word in enumerate(unique_words): # 获得词嵌入向量 word_vec = embed(torch.tensor(i)) # torch.tensor(i)就是一个标量，即固定数值 print('%3s\t' % word, word_vec)
结果：
文本分词: ['北京', '冬奥', '的', '进度条', '已经', '过半', '，', '不少', '外国', '运动员', '在', '完成', '自己', '的', '比赛', '后', '踏上', '归途', '。'] 去重后词的个数: 18 词嵌入的结果： Embedding(18, 4) 外国 tensor([-0.4085, 1.7605, -0.0886, -0.8449], grad_fn=<EmbeddingBackward0>) 归途 tensor([ 0.3770, -0.2005, 1.4169, -1.1038], grad_fn=<EmbeddingBackward0>) 。 tensor([ 0.4501, 0.3017, -1.4901, 0.3360], grad_fn=<EmbeddingBackward0>) 冬奥 tensor([ 0.6739, -0.9080, 2.3047, 1.6717], grad_fn=<EmbeddingBackward0>) 踏上 tensor([ 0.6598, -0.0093, 0.5512, -1.8283], grad_fn=<EmbeddingBackward0>) 北京 tensor([-0.9512, -0.2574, -0.4365, -0.6001], grad_fn=<EmbeddingBackward0>) 自己 tensor([-1.0887, 1.0354, -0.7965, -1.4167], grad_fn=<EmbeddingBackward0>) 在 tensor([-0.9719, 0.8727, 1.7726, 1.8527], grad_fn=<EmbeddingBackward0>) 后 tensor([-0.6442, -0.8894, 0.8813, 1.4761], grad_fn=<EmbeddingBackward0>) 过半 tensor([-1.8137, 1.0396, -0.1525, 2.3747], grad_fn=<EmbeddingBackward0>) 完成 tensor([-0.7455, -0.0772, 1.8586, -0.7208], grad_fn=<EmbeddingBackward0>) 进度条 tensor([ 0.8328, -1.9584, -0.0998, 0.2505], grad_fn=<EmbeddingBackward0>) 比赛 tensor([-0.0771, 1.9371, 2.0748, -2.5942], grad_fn=<EmbeddingBackward0>) 已经 tensor([-0.9876, -0.0267, -0.2948, -1.2054], grad_fn=<EmbeddingBackward0>) 运动员 tensor([0.5670, 0.0390, 1.0599, 0.5479], grad_fn=<EmbeddingBackward0>) ， tensor([-0.6211, -0.8672, -0.3918, -0.5938], grad_fn=<EmbeddingBackward0>) 不少 tensor([-0.9130, 0.6979, 1.1702, 1.1438], grad_fn=<EmbeddingBackward0>) 的 tensor([-0.9983, 0.0377, 0.0976, -0.4719], grad_fn=<EmbeddingBackward0>)
Embedding在机器学习中通常以矩阵的形式存在，但具体取决于上下文和应用的场景：
-
整体结构是矩阵
在自然语言处理（NLP）或推荐系统中，Embedding通常被实现为一个二维矩阵：-
行数：对应实体的数量（如词汇表大小、用户/物品数量）。
-
列数：对应嵌入向量的维度（如300维的词向量）。
-
示例：若词汇表有10,000个词，每个词用300维向量表示，则Embedding矩阵的尺寸为
10,000×300。
-
-
单个实体的Embedding是向量
每个实体（如一个词、用户或物品）的Embedding是矩阵中的一行，即一个向量。例如，单词“apple”的Embedding是该矩阵中对应行的向量。 -
动态Embedding的例外
在某些模型（如Transformer）中，Embedding可能会经过位置编码或上下文相关计算（如BERT），但底层参数仍以矩阵形式存储初始表示。
总结
-
Embedding的整体结构是矩阵，用于存储所有实体的向量表示。
-
单个实体的Embedding是该矩阵中的一个向量（一行）。
-
矩阵形式使得Embedding可以通过索引高效查询，并支持梯度下降优化。
因此，严格来说，Embedding的存储和实现是矩阵，但具体使用时提取的是其中的向量或子矩阵。
jieba.lcut
jieba.lcut是jieba分词库中的一个函数，用于精确模式分词。该函数将字符串分割成等量的中文词组，返回结果是列表类型。使用jieba.lcut时，可以通过设置参数来控制分词的行为，例如是否使用全模式（cut_all=True）或搜索引擎模式（cut_for_search=True）
使用方法
1、精确模式：使用jieba.lcut(s)函数进行精确分词，返回结果是一个列表。例如：
import jieba sentence = "我是xiaogenggou,专业是信息管理与信息系统" seg_list = jieba.lcut(sentence) print(seg_list)
结果：
['我', '是', 'xiaogenggou', ',', '专业', '是', '信息管理', '与', '信息系统']
2、全模式：使用jieba.lcut(s, cut_all=True)函数进行全模式分词，返回结果是一个列表。例如：
import jieba sentence = "我是xiaogenggou,专业是信息管理与信息系统" seg_list = jieba.lcut(sentence, cut_all=True) print(seg_list)
结果：
['我', '是', 'xiaogenggou', ',', '专业', '是', '信息', '信息管理', '管理', '与', '信息', '信息系统', '系统']
3、搜索引擎模式：使用jieba.lcut_for_search(s)函数进行搜索引擎模式分词，返回结果是一个列表。例如：
import jieba sentence = "我是xiaogenggou,专业是信息管理与信息系统" seg_list = jieba.lcut_for_search(sentence) print(seg_list)
结果：
['我', '是', 'xiaogenggou', ',', '专业', '是', '信息', '管理', '信息管理', '与', '信息', '系统', '信息系统']
三、循环神经网络RNN
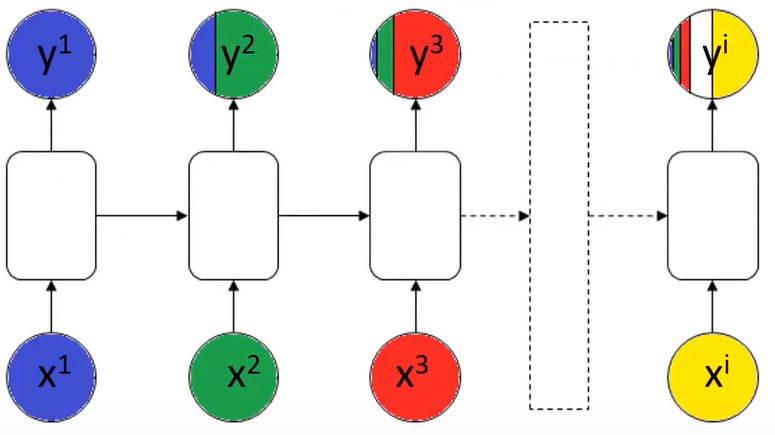
RNN(Recurrent Neural Network)，中文称作循环神经网络，它一般以序列Sequence数据为输入，通过网络内部的结构设计有效捕捉序列之间的关系特征，一般也是以序列形式进行输出。
因为RNN结构能够很好利用序列之间的关系，因此针对自然界具有连续性的输入序列，如人类的语言，语音等进行很好的处理，广泛应用于自然语言处理NLP领域的各项任务，如文本分类，情感分析，意图识别，机器翻译等．
先来看多层感知器MLP的结构：分为输入层、隐藏层、输出层。
循环神经网络：前面的序列数据用到后面的结果预测中。下图为简化的RNN结构：
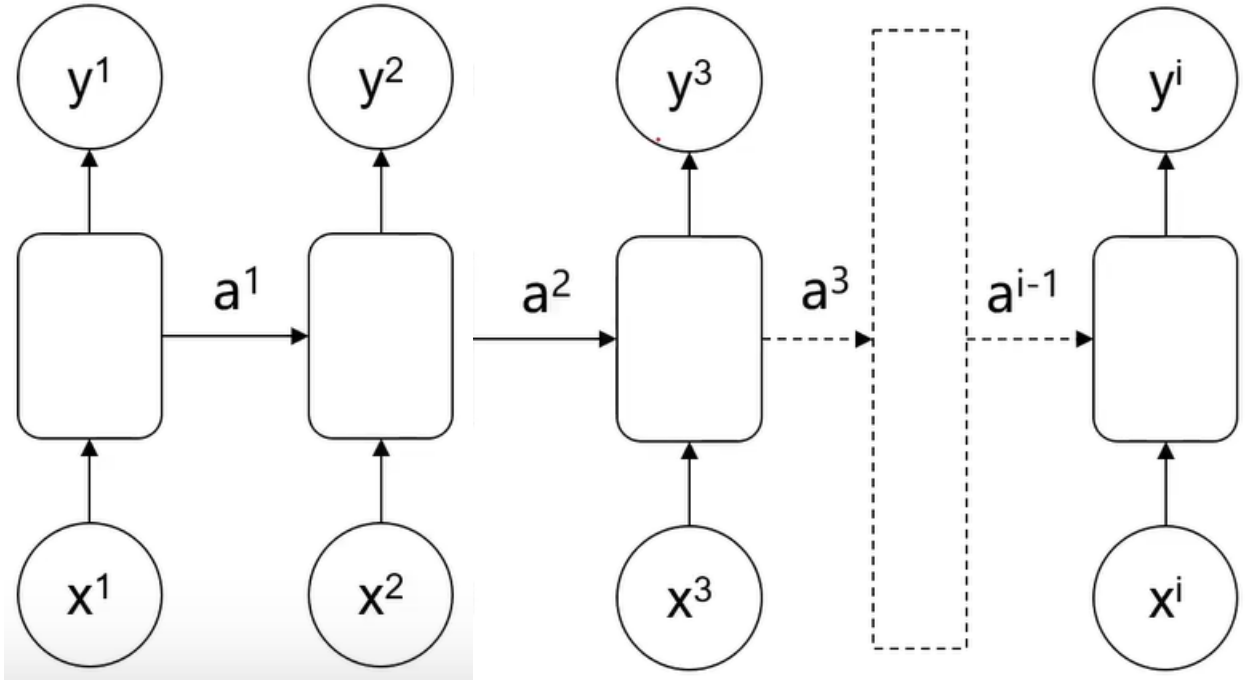
a 表示隐藏状态,每一次的输入都会包含两个值: 上一个时间步的隐藏状态a1 、当前状态的输入值x2 ，输出当前时间步的隐藏状态a2 和当前时间步的预测结果y2 。
前部序列的信息经处理后，作为输入信息传递到后部序列。即输入x1 后，除了得到预测结果y1 ，还得到a1 ，a1 包含前面序列的部分信息，再把a1 和x2 输入得到预测结果y2 ，这样的话y2 的预测结果与前面的输入x1 是有一定的关系的。
1、RNN模型的分类
这里我们将从两个角度对RNN模型进行分类．第一个角度是输入和输出的结构，第二个角度是RNN的内部构造．
按照输入和输出的结构进行分类：
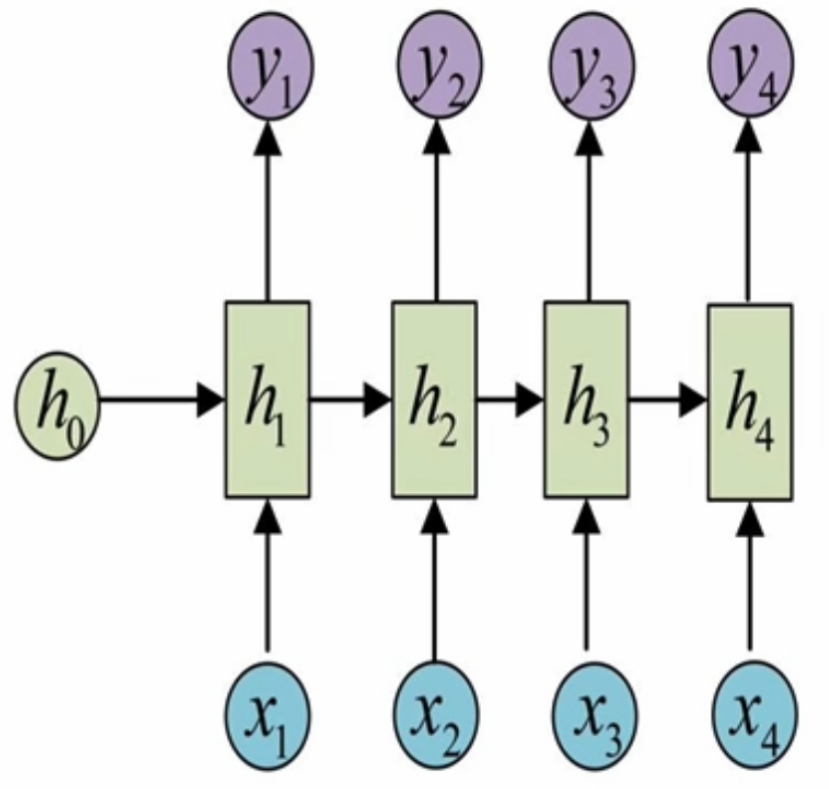
（1）、多输入对多输出、维度相同RNN结构（N vs N-RNN）
它是RNN最基础的结构形式，最大的特点就是：输入和输出序列是等长的．由于这个限制的存在，使其适用范围比较小，可用于生成等长度的合辙诗句．
（2）、多输入单输出RNN结构（N vs 1-RNN）
有时候我们要处理的问题输入是一个序列，而要求输出是一个单独的值而不是序列，要在最后一个隐层输出h上进行线性变换。
大部分情况下，为了更好的明确结果，还要使用sigmoid或者softmax进行处理．这种结构经常被应用在文本分类问题上．
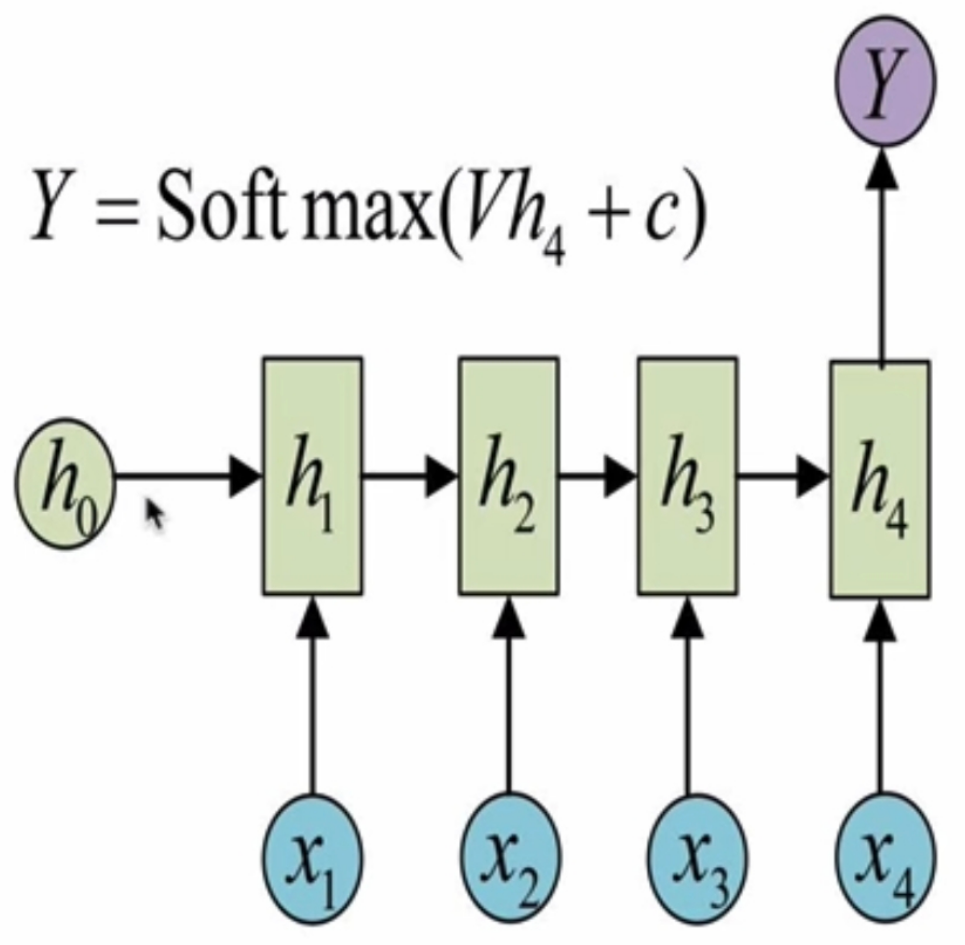
（3）、单输入多输出RNN结构（1 vs N-RNN）
我们最常采用的一种方式就是使该输入作用于每次的输出之上．这种结构可用于将图片生成文字任务等．
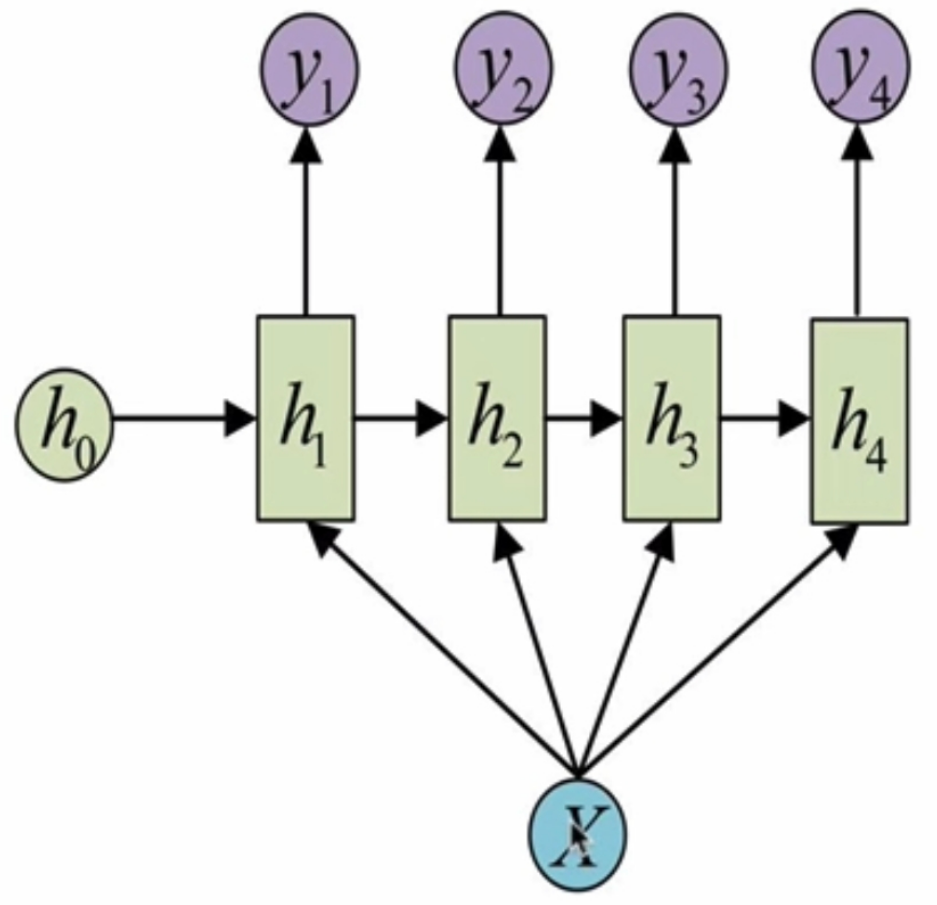
（4）、多输入对多输出、维度不同RNN结构（N vs M-RNN）
这是一种不限输入输出长度的RNN结构，它由编码器和解码器两部分组成，两者的内部结构都是某类RNN，它也被称为seq2seq架构。
输入数据首先通过编码器，最终输出一个隐含变量c，之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上，以保证输入信息被有效利用。
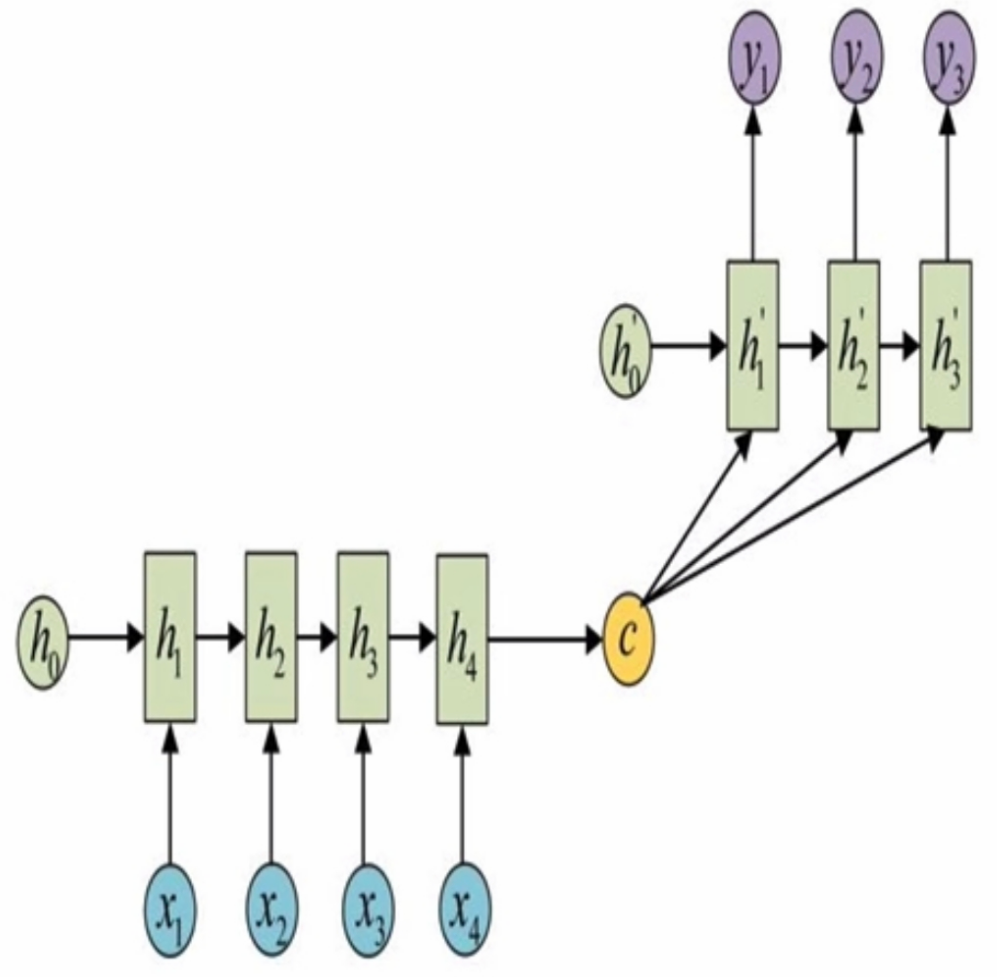
按照RNN的内部构造进行分类：
（1）、传统RNN
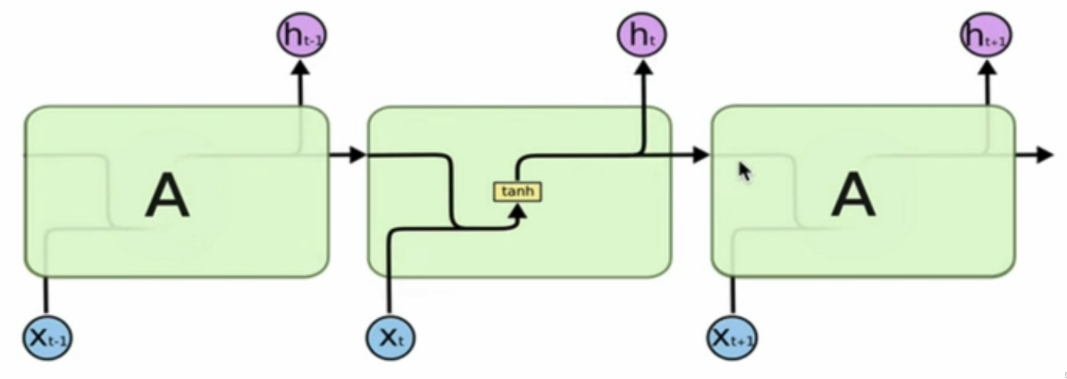传统RNN结构只通过一个箭头串联
内部计算函数
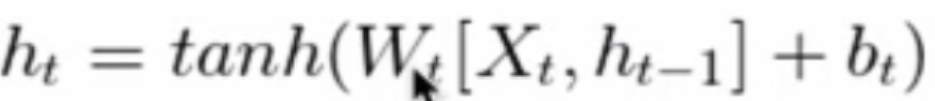
tanh的作用： 用于帮助调节流经网络的值，tanh函数将值压缩在﹣1和1之间。
传统RNN的优势：
由于内部结构简单，对计算资源要求低，相比之后我们要学习的RNN变体LSTM和GRU模型参数总量少了很多，在短序列任务上性能和效果都表现优异。
传统rnn的缺点：
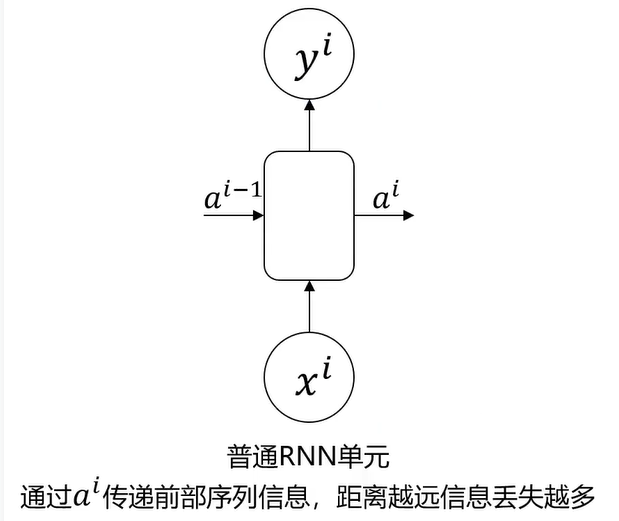
传统RNN在解决长序列之间的关联时，通过实践，证明经典RNN表现很差，原因是在进行反向传播的时候，过长的序列导致梯度的计算异常，发生梯度消失或爆炸。
前部序列信息在传递到后部的同时，信息权重下降，导致重要信息丢失。
例子: 第一句填入was,第二句填入were
答案是was还是were取决于前面是student还是students,但是前面序列的信息传递到后面时,信息权重下降,导致重要信息丢失.
解决办法:需要提高前部特定信息的决策权重
四、掌握传统RNN网络原理
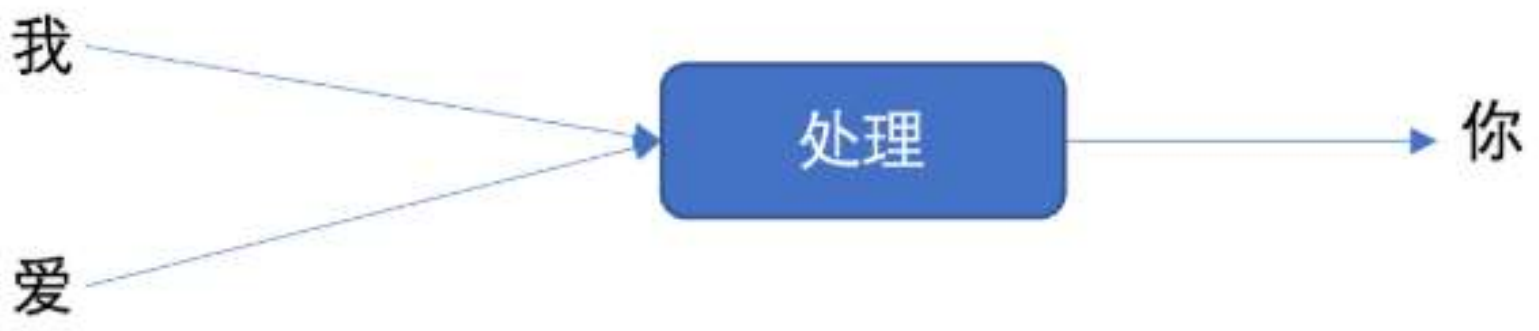
文本数据是具有序列特性的
例如: "我爱你", 这串文本就是具有序列关系的，"爱" 需要在 "我" 之后，"你" 需要在 "爱" 之后, 如果颠倒了顺序，那么可能就会表达不同的意思。
为了表示出数据的序列关系，需要使用循环神经网络(Recurrent Nearal Networks, RNN) 来对数据进行建模，RNN 是一个作用于处理带有序列特点的样本数据。
RNN 是如何计算过程是什么样的呢？
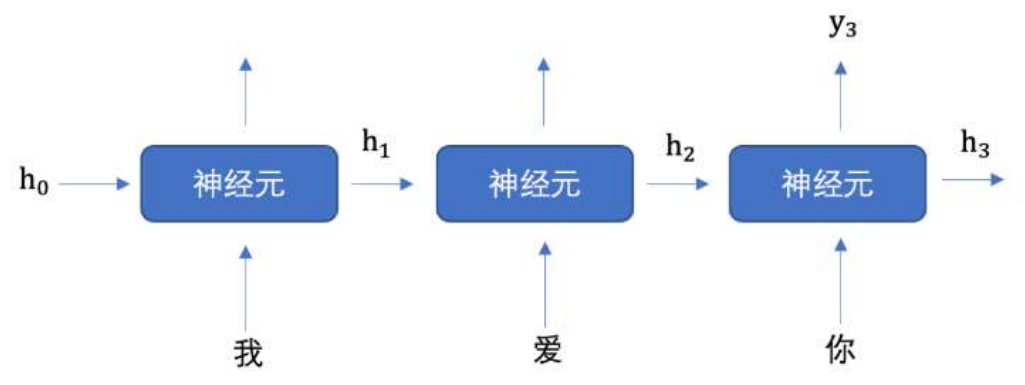
h 表示隐藏状态,
每一次的输入都会包含两个值: 上一个时间步的隐藏状态、当前状态的输入值，输出当前时间步的隐藏状态和当前时间步的预测结果。你可以看到非常重要的一点，就是输入序列长度与输出序列长度是相同的。这种输入和输出数据项数一致的 RNN，一般叫做 N vs.N 的 RNN。
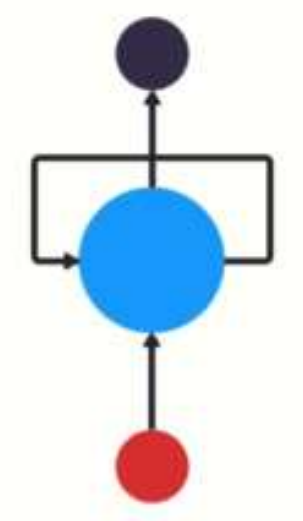
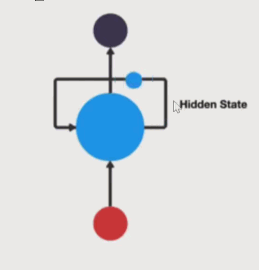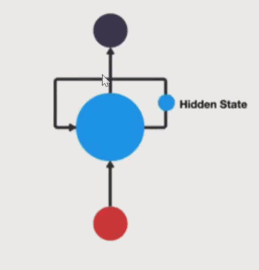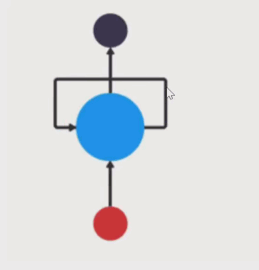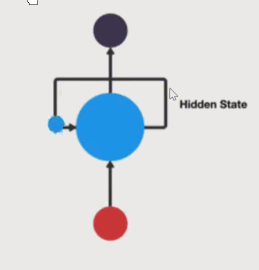
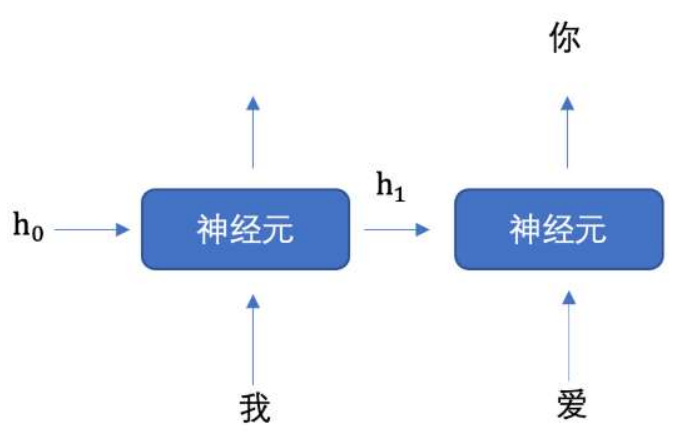
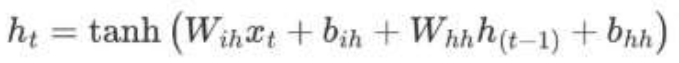
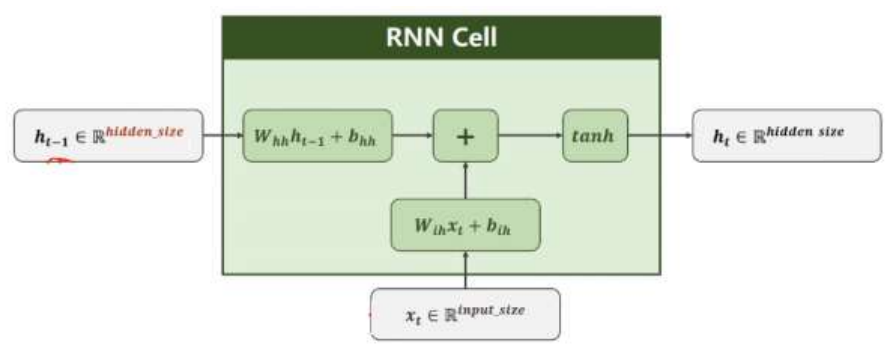
上述公式中: xt 表示词向量，ht-1 表示隐藏状态矩阵
1. Wih 表示输入数据的权重
2. bih 表示输入数据的偏置
3. Whh 表示输入隐藏状态的权重
4. bhh 表示输入隐藏状态的偏置
最后对输出的结果使用 tanh 激活函数进行计算，得到该神经元你的输出。
1、掌握PyTorch RNN API
这里用默认pytorch的RNN
RNN = torch.nn.RNN(input_size,hidden_size，num_layer)
参数意义是：
1. input_size：输入数据的维度，一般设为词向量的维度；
2. hidden_size：隐藏层h的维数，也是当前层神经元的输出维度；
3. num_layer: 隐藏层h的层数，默认为1.
将RNN实例化就可以将数据送入进行处理。
⚫ 输入数据和输出结果
将RNN实例化就可以将数据送入其中进行处理，处理的方式如下所示：
output, hn = RNN(x, h0)
◼ 输入数据:输入主要包括词嵌入的x 、初始的隐藏层h0
x的表示形式为[seq_len, batch, input_size]，即[句子的长度，batch的大小，词向量的维度]
h0的表示形式为[num_layers, batch, hidden_size]，即[隐藏层的层数，batch的大，隐藏层h的维数]
◼ 输出结果：主要包括输出结果output,最后一层的hn
output的表示形式与输入x类似，为[seq_len, batch, hidden_size]，即[句子的长度，batch的大小，输出向量的维度]
hn的表示形式与输入h0一样，为[num_layers, batch, hidden_size]，即[隐藏层的层数，batch的大，隐藏层h的维度]
import torch
import torch.nn as nn
# RNN层送入批量数据
def test():
# 词向量维度 128, 隐藏向量维度 256
rnn = nn.RNN(input_size=128, hidden_size=256)
# 第一个数字: 表示句子长度,也就是词语个数
# 第二个数字: 批量个数，也就是句子的个数
# 第三个数字: 词向量维度
inputs = torch.randn(5, 32, 128)
hn = torch.zeros(1, 32, 256) # 隐藏层的层数为1，隐藏层的维数为256
# 获取输出结果
output, hn = rnn(inputs, hn)
print("输出向量的维度：\n",output.shape)
print("隐含层输出的维度：\n",hn.shape)
if __name__ == '__main__':
test()
输入维度为 (seq_len, batch_size, input_size)
结果:
输出向量的维度： torch.Size([5, 32, 256]) 隐含层输出的维度： torch.Size([1, 32, 256])
下面通过代码来理解从词嵌入层到RNN层的过程
import torch
import torch.nn as nn
import jieba
if __name__ == '__main__':
# 0.文本数据(语料)
text = '北京冬奥的进度条已经过半，不少外国运动员在完成自己的比赛后踏上归途。'
# 1. 文本分词
words = jieba.lcut(text)
print('文本分词:', words)
all_words = [] # 所有的
all_words.append(words)
print('all_words:', all_words)
# 2.分词去重并保留原来的顺序获取所有的词语
# unique_words = list(set(words)) # 注意：如果用set去重的话，数据就没有了序列关系
unique_words = [] # 去重的
# 遍历分词结果，去重后存储到unique_words
for word in words:
if word not in unique_words:
unique_words.append(word)
print("去重后词的个数:",len(unique_words)) # 此时的unique_words带了数据的序列关系
# 语料中词的数量
word_count = len(unique_words) # 18
# 词到索引映射
word_to_index = {word: idx for idx, word in enumerate(unique_words)}
print("词到索引映射",word_to_index)
# 词表索引表示
corpus_idx = [] # 即将分词后的词用索引表示
for words in all_words:
temp = []
# 获取每一行的词，并获取相应的索引
for word in words:
temp.append(word_to_index[word])
# 获取当前文档中每个词对应的索引
corpus_idx.extend(temp) # extend:将可迭代对象中的所有元素逐一添加到列表中
print("当前文档中每个词对应的索引", corpus_idx)
# 3. 构建词嵌入层:num_embeddings: 表示词的总数量;embedding_dim: 表示词嵌入的维度
ebd = nn.Embedding(word_count, embedding_dim=10) # 词嵌入层
print("词嵌入的结果：",ebd) # 18行10列的矩阵
inputs = torch.tensor([[ 15]]) # 假设取1个词（这里为‘踏上’）来进行训练
print("输入值：：", inputs)
print("输入值的形状：",inputs.shape)
embed = ebd(inputs) # 词索引的向量化表示
print("词嵌入层矩阵embed的值：",embed) # 词索引对应的向量，即为该词对应的数值化后的向量表示
print("词嵌入层矩阵embed的形状：", embed.shape) # torch.Size([1, 1, 10])
# 修改维度: (seq_len, batch,词向量维度 128)
rnn = nn.RNN(10, 10, 1, batch_first=True) # RNN层 参数分别为词向量的维度10、隐藏层的输出维度10、隐藏层的层数（默认为1）
print("embed将0维和1维进行交换：", embed.transpose(0, 1))
print("embed将0维和1维进行交换后的形状：", embed.transpose(0, 1).shape) # torch.Size([1, 1, 10])
h0 = torch.zeros(1, 1, 10) # 初始隐藏状态
print("初始隐藏状态：", h0) #tensor([[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]])
output, hidden = rnn(embed.transpose(0, 1), h0) # 将数据送入RNN层进行处理
print("输出值：",output)
print("输出值的形状：", output.shape) # torch.Size([1, 1, 10])
print("输出隐藏状态：",hidden)
print("输出隐藏状态的形状：", hidden.shape) # torch.Size([1, 1, 10])
结果：
文本分词: ['北京', '冬奥', '的', '进度条', '已经', '过半', '，', '不少', '外国', '运动员', '在', '完成', '自己', '的', '比赛', '后', '踏上', '归途', '。']
all_words: [['北京', '冬奥', '的', '进度条', '已经', '过半', '，', '不少', '外国', '运动员', '在', '完成', '自己', '的', '比赛', '后', '踏上', '归途', '。']]
去重后词的个数: 18
词到索引映射 {'北京': 0, '冬奥': 1, '的': 2, '进度条': 3, '已经': 4, '过半': 5, '，': 6, '不少': 7, '外国': 8, '运动员': 9, '在': 10, '完成': 11, '自己': 12, '比赛': 13, '后': 14, '踏上': 15, '归途': 16, '。': 17}
当前文档中每个词对应的索引 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 2, 13, 14, 15, 16, 17]
词嵌入的结果： Embedding(18, 10)
输入值：： tensor([[15]])
输入值的形状： torch.Size([1, 1])
词嵌入层矩阵embed的值： tensor([[[-2.4527e+00, -5.2673e-01, 9.3914e-02, -1.3524e-01, -1.2005e+00,
1.7711e-03, -3.8930e-01, -6.9891e-02, -1.7490e+00, -7.9795e-01]]],
grad_fn=<EmbeddingBackward0>)
词嵌入层矩阵embed的形状： torch.Size([1, 1, 10])
embed将0维和1维进行交换： tensor([[[-2.4527e+00, -5.2673e-01, 9.3914e-02, -1.3524e-01, -1.2005e+00,
1.7711e-03, -3.8930e-01, -6.9891e-02, -1.7490e+00, -7.9795e-01]]],
grad_fn=<TransposeBackward0>)
embed将0维和1维进行交换后的形状： torch.Size([1, 1, 10])
初始隐藏状态： tensor([[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]])
输出值： tensor([[[-0.6871, -0.5690, -0.6201, -0.1067, 0.8188, 0.5810, 0.6865,
-0.8248, -0.4414, -0.2037]]], grad_fn=<TransposeBackward1>)
输出值的形状： torch.Size([1, 1, 10])
输出隐藏状态： tensor([[[-0.6871, -0.5690, -0.6201, -0.1067, 0.8188, 0.5810, 0.6865,
-0.8248, -0.4414, -0.2037]]], grad_fn=<StackBackward0>)
输出隐藏状态的形状： torch.Size([1, 1, 10])
用下面的图来表示：
h0为[[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]]
x1为 [[[-2.4527e+00, -5.2673e-01, 9.3914e-02, -1.3524e-01, -1.2005e+00, 1.7711e-03, -3.8930e-01, -6.9891e-02, -1.7490e+00, -7.9795e-01]]]
h1为 [[[-0.6871, -0.5690, -0.6201, -0.1067, 0.8188, 0.5810, 0.6865, -0.8248, -0.4414, -0.2037]]]
y1为 [[[-0.6871, -0.5690, -0.6201, -0.1067, 0.8188, 0.5810, 0.6865, -0.8248, -0.4414, -0.2037]]]
2、手写一个传统RNN的前向传播过程
手写一个传统RNN帮我们深入了解RNN的工作原理
上面用的是pytorch的RNN，下面的是deepseek帮我们手写一个RNN
import torch
import torch.nn as nn
class SimpleRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleRNN, self).__init__()
self.hidden_size = hidden_size
# 权重参数
self.Wxh = nn.Parameter(torch.randn(input_size, hidden_size)) # 输入到隐藏层，输入数据的权重
self.Whh = nn.Parameter(torch.randn(hidden_size, hidden_size)) # 隐藏层到隐藏层,输入隐藏状态的权重，每一轮都只有一个隐藏层
self.Why = nn.Parameter(torch.randn(hidden_size, output_size)) # 隐藏层到输出，输出隐藏状态的权重
# 偏置项
self.bh = nn.Parameter(torch.zeros(hidden_size)) # 8维
self.by = nn.Parameter(torch.zeros(output_size)) # 2维
def forward(self, x, hidden_state):
"""
x: 输入序列 (seq_len, input_size)
hidden_state: 刚开始为初始隐藏状态 (hidden_size,)，
"""
outputs = []
print(x.size(0)) # x.size(0)会返回张量x的第一个维度的大小，x的维度为[5,3],即值为5
for t in range(x.size(0)): # 按时间步循环 x.size(0) 值为5
# 当前时间步的输入
xt = x[t] # 取出二维矩阵x每行的数组
print("每一个词向量：",xt) # tensor([ 1.1127, -0.1445, -2.0122])
# RNN核心计算
hidden_state = torch.tanh(
torch.matmul(xt, self.Wxh) + # torch.matmul表示进行点积运算，即将输入的单个词的词向量与输入数据的权重进行点积运算
torch.matmul(hidden_state, self.Whh) + # 隐藏状态与输入隐藏状态的权重进行点积运算
self.bh # 偏置 ，即只加一个偏置
) # (hidden_size,)
# 输出层计算
yt = torch.matmul(hidden_state, self.Why) + self.by # 输出隐藏状态与输出隐藏状态权重进行点积运算，再加上偏置
outputs.append(yt) # yt的值如下：nsor([1.2658, 2.0378], grad_fn=<AddBackward0>)
print(outputs) # 最终输入结果
return torch.stack(outputs), hidden_state
if __name__ == "__main__":
# 参数设置
input_size = 3 # 输入特征维度 词的维度
hidden_size = 8 # 隐藏层维度
output_size = 2 # 输出维度
seq_len = 5 # 序列长度, 词的个数
# 初始化RNN
rnn = SimpleRNN(input_size, hidden_size, output_size)
# 随机输入和初始隐藏状态
x = torch.randn(seq_len, input_size) # 随机生成5行3列的二维矩阵，即表示5个词进行词嵌入后，词的向量表示
print("输入的值为：",x)
hidden = torch.zeros(hidden_size) # 初始隐藏状态 tensor([0., 0., 0., 0., 0., 0., 0., 0.])
print("初始隐藏状态为：", hidden)
# 前向传播
outputs, final_hidden = rnn(x, hidden)
print("Output:", outputs) # torch.Size([5, 2])，即5行3列的矩阵，输出为5行2列的矩阵
print("Output shape:", outputs.shape) # (seq_len, output_size)
print("Final hidden state:", final_hidden) # [ 9.9123e-01, -9.2621e-01, 9.9919e-01, 9.9781e-01, -6.0391e-04, -9.8622e-01, -8.5304e-01, 6.3166e-01]
print("Final hidden state shape:", final_hidden.shape) # torch.Size([8])，即一维数组
结果：
输入的值为： tensor([[ 1.1127, -0.1445, -2.0122],
[-0.1048, 0.0261, -0.7098],
[-1.9862, -0.0552, 1.1918],
[ 1.0842, 0.6633, -0.5385],
[ 1.6510, -1.2584, 0.2170]])
初始隐藏状态为： tensor([0., 0., 0., 0., 0., 0., 0., 0.])
5
每一个词向量： tensor([ 1.1127, -0.1445, -2.0122])
[tensor([1.2658, 2.0378], grad_fn=<AddBackward0>)]
每一个词向量： tensor([-0.1048, 0.0261, -0.7098])
[tensor([1.2658, 2.0378], grad_fn=<AddBackward0>), tensor([ 1.3628, -1.2764], grad_fn=<AddBackward0>)]
每一个词向量： tensor([-1.9862, -0.0552, 1.1918])
[tensor([1.2658, 2.0378], grad_fn=<AddBackward0>), tensor([ 1.3628, -1.2764], grad_fn=<AddBackward0>), tensor([-1.1195, -2.9322], grad_fn=<AddBackward0>)]
每一个词向量： tensor([ 1.0842, 0.6633, -0.5385])
[tensor([1.2658, 2.0378], grad_fn=<AddBackward0>), tensor([ 1.3628, -1.2764], grad_fn=<AddBackward0>), tensor([-1.1195, -2.9322], grad_fn=<AddBackward0>), tensor([-0.9157, 1.2355], grad_fn=<AddBackward0>)]
每一个词向量： tensor([ 1.6510, -1.2584, 0.2170])
[tensor([1.2658, 2.0378], grad_fn=<AddBackward0>), tensor([ 1.3628, -1.2764], grad_fn=<AddBackward0>), tensor([-1.1195, -2.9322], grad_fn=<AddBackward0>), tensor([-0.9157, 1.2355], grad_fn=<AddBackward0>), tensor([1.0795, 0.1543], grad_fn=<AddBackward0>)]
Output: tensor([[ 1.2658, 2.0378],
[ 1.3628, -1.2764],
[-1.1195, -2.9322],
[-0.9157, 1.2355],
[ 1.0795, 0.1543]], grad_fn=<StackBackward0>)
Output shape: torch.Size([5, 2])
Final hidden state: tensor([ 9.9123e-01, -9.2621e-01, 9.9919e-01, 9.9781e-01, -6.0391e-04,
-9.8622e-01, -8.5304e-01, 6.3166e-01], grad_fn=<TanhBackward0>)
Final hidden state shape: torch.Size([8])
用下面的图来表示：
x表示输入层，h表示隐藏层，y表示输出层
隐藏层的计算如下：
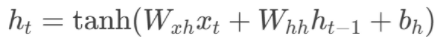
输出层的计算如下：
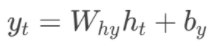
使用线形层n.Linear()来实现输出层：n.Linear() 是 PyTorch 中定义全连接层（也称为线性层、全连接层或密集层）的函数。它的作用是对输入数据进行线性变换，也就是矩阵乘法操作，具体地说，它的作用是对输入向量进行线性变换并加上偏置，从而输出一个新的向量。
代码如下：
self.out = nn.Linear(128, word_count)
与PyTorch原生RNN对比
PyTorch的 nn.RNN 已经优化过，支持批量处理、多层RNN等特性。我们的简单实现有以下区别：
-
不支持批量处理（需要处理
batch_dim） -
没有实现梯度裁剪等优化
-
未提供
num_layers等高级参数
扩展建议
-
处理批量数据：
修改输入维度为(seq_len, batch_size, input_size)，并在计算中维护批量维度。 -
实现LSTM/GRU：
添加门控机制（输入门、遗忘门、输出门）。 -
双向RNN：
增加反向传播的隐藏状态计算。
如果需要一个生产可用的RNN，建议直接使用 torch.nn.RNN，但手写实现能帮助深入理解RNN的工作原理。
五、LSTM(Long Short-Term Memory)长短期记忆网络
RNN是想把所有信息都记住，不管是有用的信息还是没用的信息。LSTM:设计一个记忆细胞，具备选择性记忆的功能，可以选择记忆重要信息，过滤掉噪声信息，减轻记忆负担。
有没有可能增加一项,这一项把前面的重要信息存在里面,在传递的过程中信息保留住
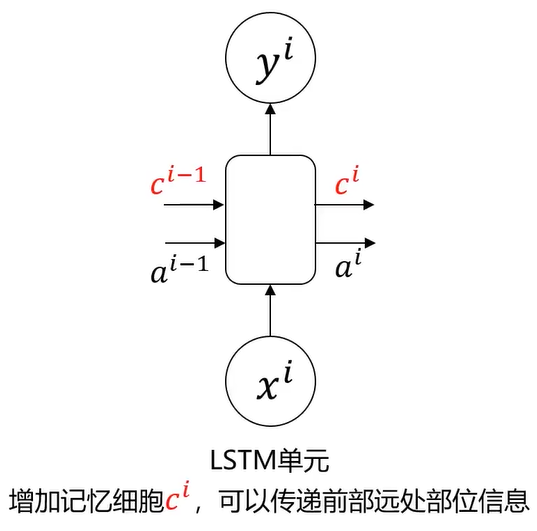
ci 主要是记住重要的信息
简化理解:相比ai ，记忆细胞ci 重点记录前部序列重要信息，且在传递过程中信息丢失少
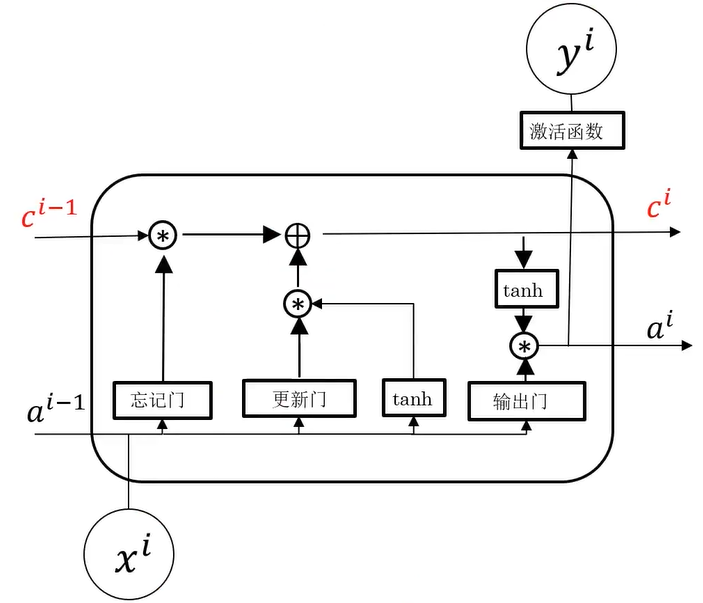
忘记门:选择性丢弃ai-1与xi 中不重要的信息
更新门:确定给记忆细胞添加哪些信息
输出门:筛选需要输出的信息
特点:
在网络结构很深(很多层)的情况下，也能保留重要信息，解决了普通RNN求解过程中的梯度消失问题
LSTM (Long Short-Term Memory）也称长短时记忆结构，它是传统RNN的变体，与经典RNN相比能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象，同时LSTM的结构更复杂。
LSTM缺点：由于内部结构相对较复杂，因此训练效率在同等算力下较传统RNN低很多．
LSTM优势：LSTM的门结构能够有效减缓长序列问题中可能出现的梯度消失或爆炸，虽然并不能杜绝这种现象，但在更长的序列问题上表现优于传统RNN.
1、LSTM的前向传播
LSTM有三个门：遗忘门、输入门、输出门，还有细胞状态。每个门都有各自的权重和激活函数。输入门控制新信息的流入，遗忘门决定丢弃哪些旧信息，输出门则基于当前状态和输入生成最终的隐藏状态。
前向传播的过程。需要按步骤计算遗忘门、输入门、候选细胞状态、更新细胞状态、输出门，最后得到隐藏状态。每个步骤的激活函数也要注意，遗忘门和输入门用sigmoid，候选状态用tanh，输出门同样用sigmoid，隐藏状态再用tanh处理细胞状态。
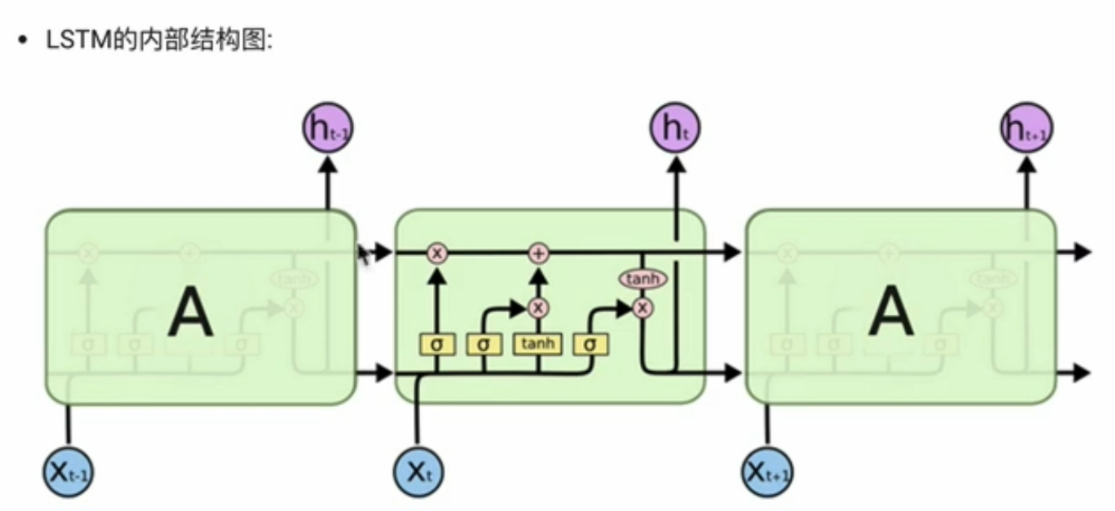LSTM用两个箭头进行串联
pointwise Operation表示逐点乘法运算，concatenate表示合并并串联，copy表示其内容被复制，且转到不同的位置。C表示记忆细胞Cell,
传统RNN只有一个神经网络层，而LSTM有四个神经网络层。
门:
门是一种有选择的让信息通过的方式，他们由一个sigmoid神经网络层和一个逐点乘法运算组成，σ表示sigmoid神经网络层，sigmoid输出0-1之间的数字，描述应该让多少成分通过，值为0表示不让任何东西通过，值为1表示让一切都通过，LSTM具有3个这样的门，以保护和控制单元状态，
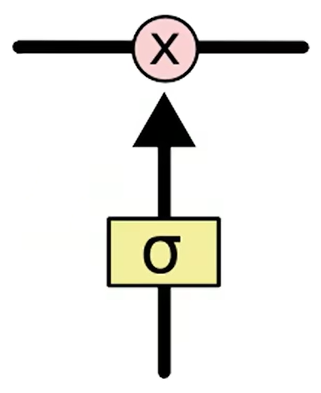
它的核心结构可以分为四个部分去解析：
遗忘门（forget）：决定我们要从细胞状态中丢弃哪些信息，以ht-1和xt为输入，输出一个介于0-1的值。
σ表示sigmoid神经网络层，sigmoid输出0-1之间的数字，描述应该让多少成分通过，值为0表示不让任何东西通过，值为1表示让一切都通过，LSTM具有3个这样的门，以保护和控制单元状态，
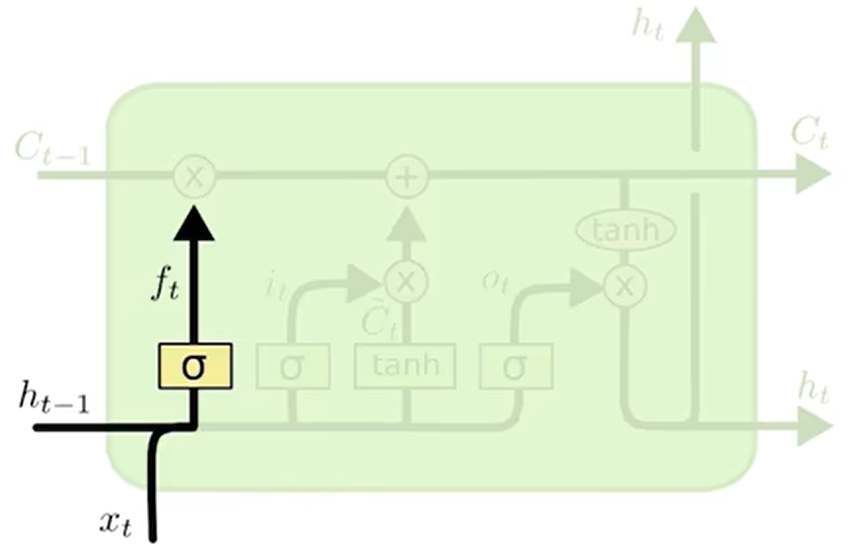
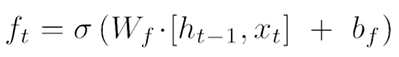
权重矩阵和偏置向量的维度需要正确设置。比如，输入维度是input_size，隐藏层维度是hidden_size，那么每个门的权重应该是[input_size + hidden_size, hidden_size]，因为输入和隐藏状态是拼接在一起的。而偏置则是hidden_size维的向量。
输入门（input）：决定要在cell状态中存储哪些更新信息，这有两个部分，首先称为“输入门层”的sigmoid层决定更新哪些值，接下来一个tanh层创建一个新候选值的向量，可以将其添加到状态中，在下一步中将结合来创建对状态的更新，
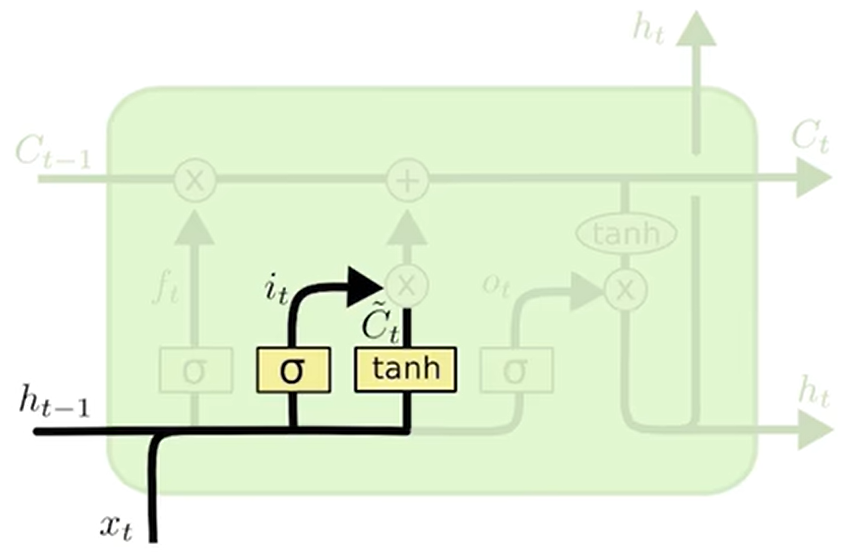
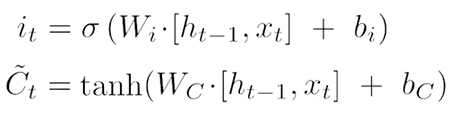
更新细胞状态
接着，将旧状态乘以ft,然后添加
,根据决定更新每个状态值的缩放程度进行缩放，在语言模型的情况下，这是我们实际上要删除有关旧主题信息并添加新信息的地方，
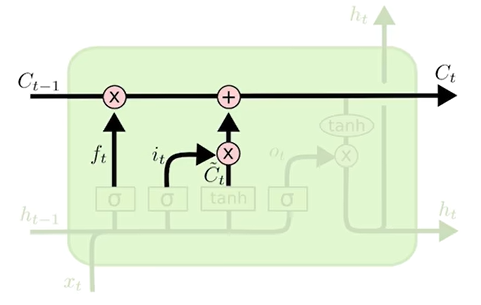
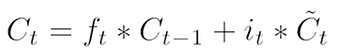
细胞状态的更新是遗忘门乘以旧状态加上输入门乘以候选状态。
在LSTM的每个时间步里面，都有一个记忆cell，这个东西给与了LSTM选择记忆功能使得LSTM有能力自由选择每个时间步里面记忆的内容
细胞状态(Cell)
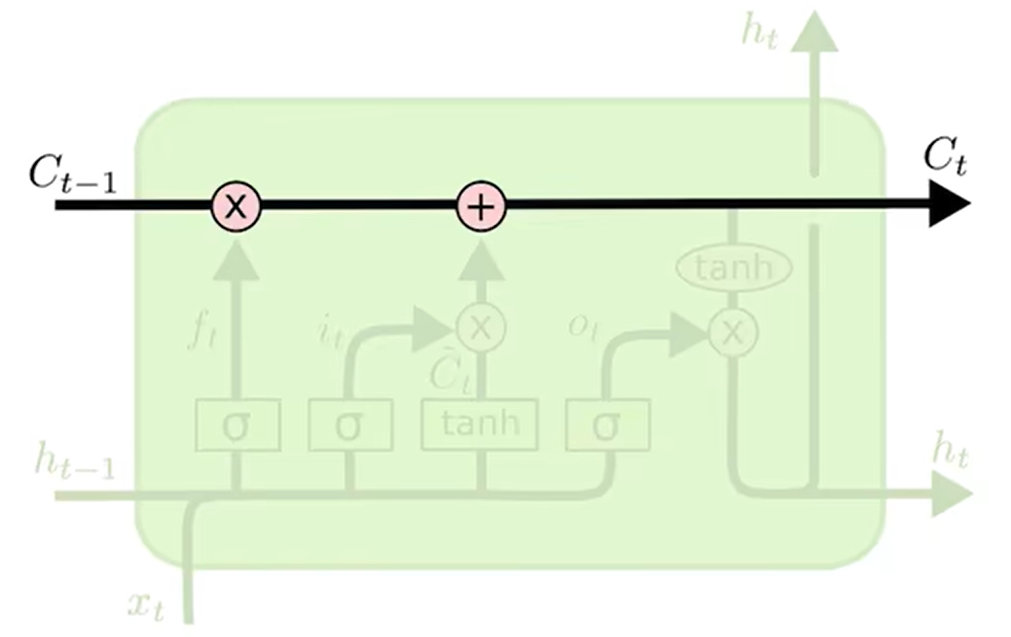
LSTM确实有能力删除或添加信息到细胞状态
输出门（output）：我们需要决定输出什么，此输出将基于我们的细胞状态，但将是过滤后的版本，首先我们运行一个sigmoid层， 它决定我们要输出细胞状态的哪些部分，然后我们将细胞状态通过tanh（将值转化到-1到1之间）并将其乘以sigmoid门的输出，这样我们就只输出我们决定输出的部分，
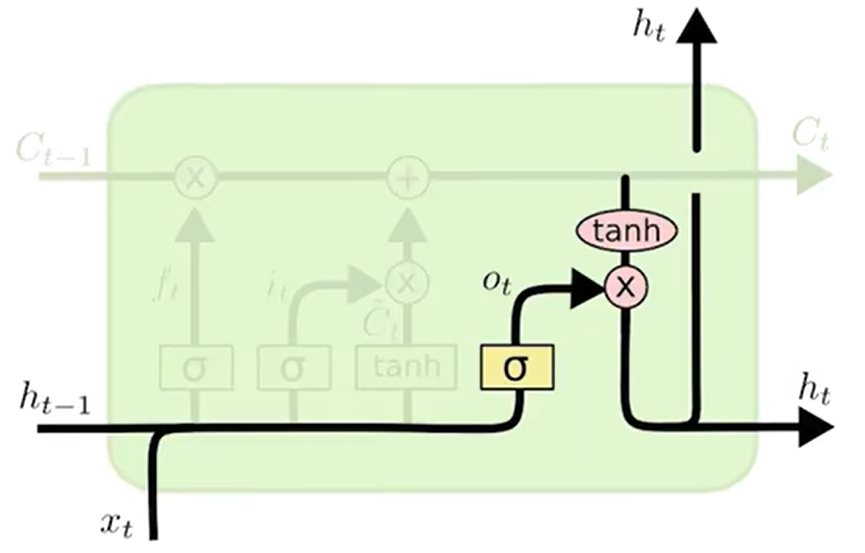
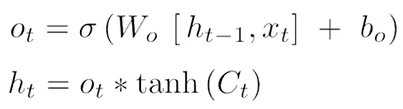
总结:
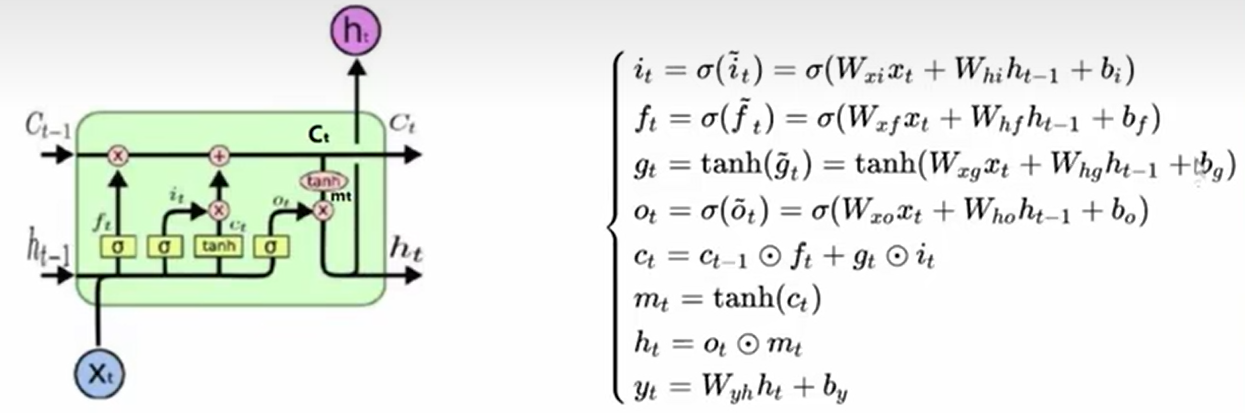
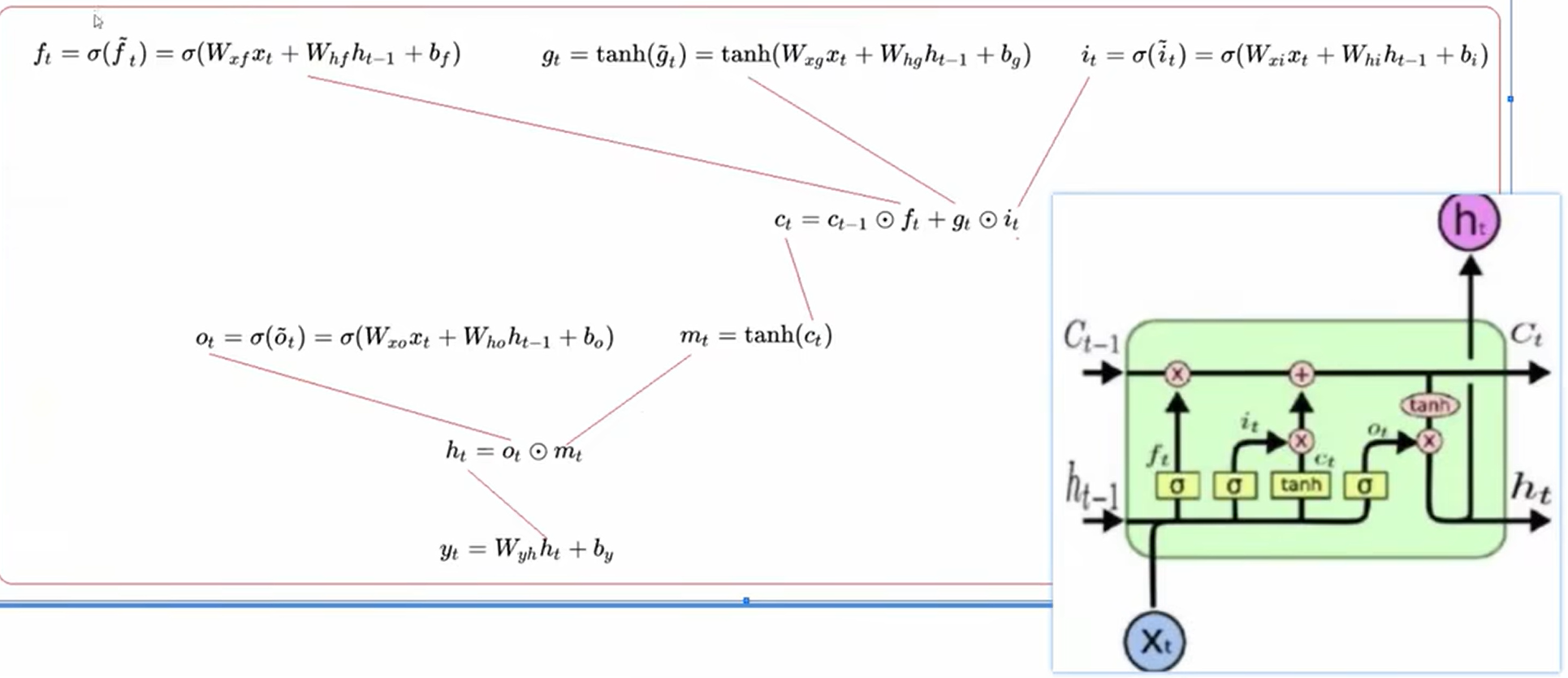
2、手写一个LSTM的前向传播过程
手写一个LSTM帮我们深入了解LSTM的工作原理
注意：
（1）、输入数据的形状，比如输入x是一个时间步的数据，形状为(batch_size, input_size)，而之前的隐藏状态和细胞状态可能需要初始化为零。不过在这个简化的例子中，可能暂时不考虑批量处理，只处理单个样本。
（2）、激活函数的使用是否正确也很重要。比如，sigmoid函数用于门控，将值压缩到0-1之间，表示信息的通过比例；tanh用于候选细胞状态和隐藏状态，将值压缩到-1到1之间，帮助调节梯度流动。
（3）、可能用户会想知道如何训练这个LSTM，比如反向传播的过程，但在这个阶段可能不需要实现，因为重点在前向传播的结构。所以可以暂时忽略训练部分，专注于前向计算。
import numpy as np class LSTM_Cell: def __init__(self, input_size, hidden_size): # 参数初始化 hidden_size为隐藏状态的维度 self.hidden_size = hidden_size # 输入门参数 self.W_xi = np.random.randn(input_size, hidden_size) * 0.01 # 输入数据的权重 形状为（32，64） self.W_hi = np.random.randn(hidden_size, hidden_size) * 0.01 # 输入隐藏状态的权重 形状为（64，64） self.b_i = np.zeros((1, hidden_size)) # 输入门偏置 形状为（1，64） # 遗忘门参数 self.W_xf = np.random.randn(input_size, hidden_size) * 0.01 # 输入数据的权重 形状为（32，64） self.W_hf = np.random.randn(hidden_size, hidden_size) * 0.01 # 输入隐藏状态的权重 形状为（64，64） self.b_f = np.zeros((1, hidden_size)) # 遗忘门偏置 形状为（1，64） # 候选记忆参数 self.W_xc = np.random.randn(input_size, hidden_size) * 0.01 # 输入数据的权重 形状为（32，64） self.W_hc = np.random.randn(hidden_size, hidden_size) * 0.01 # 输入隐藏状态的权重 形状为（64，64） self.b_c = np.zeros((1, hidden_size)) # 候选记忆偏置 形状为（1，64） # 输出门参数 self.W_xo = np.random.randn(input_size, hidden_size) * 0.01 # 输入数据的权重 形状为（32，64） self.W_ho = np.random.randn(hidden_size, hidden_size) * 0.01 # 输入隐藏状态的权重 形状为（64，64） self.b_o = np.zeros((1, hidden_size)) # 输出门偏置 形状为（1，64） def sigmoid(self, x): return 1 / (1 + np.exp(-x)) # sigmoid函数的公式 def tanh(self, x): return np.tanh(x) # tanh双曲正切函数 def forward(self, x, h_prev, c_prev): """ 前向传播 参数: x - 当前时间步输入 (batch_size, input_size) h_prev - 前一时间步隐藏状态 (batch_size, hidden_size) c_prev - 前一时间步细胞状态 (batch_size, hidden_size) """ # 输入维度是input_size，隐藏层维度是hidden_size，那么每个门的权重应该是[input_size + hidden_size, hidden_size]， # 因为输入和隐藏状态是拼接在一起的。而偏置则是hidden_size维的向量。 # 拼接输入和上一个隐藏状态 combined = np.concatenate((x, h_prev), axis=1) print("x的形状", x.shape) # x的形状 (1, 32) print("h_prev的形状", h_prev.shape) # (1, 64) print("combined的形状", combined.shape) # (1, 96) # 遗忘门计算 np.dot表示点积 x的形状 (1, 32) W_xf的形状(32, 64)，点积运算得到(1, 64) # h_prev的维度（1，64），W_hf的维度为（64，64），点积运算得到（1，64） # b_f的维度为（1，64） f = self.sigmoid( # 注意：用sigmoid函数对一维数组进行运算实际上是对数组中的每一个值进行sigmoid计算，数组维度不变 np.dot(x, self.W_xf) + # 遗忘门：输入数据与输入数据的权重进行点积运算 np.dot(h_prev, self.W_hf) + # 遗忘门：前一时间步隐藏状态 与 输入隐藏状态的权重 进行点积运算 self.b_f # 遗忘门的偏置 ) print("遗忘门的值为：", f) print("遗忘门的形状为：", f.shape) # (1, 64) # 输入门计算 i = self.sigmoid( np.dot(x, self.W_xi) + # 输入门：输入数据与输入数据的权重进行点积运算 np.dot(h_prev, self.W_hi) + # 输入门：前一时间步隐藏状态 与 输入隐藏状态的权重 进行点积运算 self.b_i # 输入门的偏置 ) # 候选记忆计算 c_hat = self.tanh( np.dot(x, self.W_xc) + # 候选记忆：输入数据与输入数据的权重进行点积运算 np.dot(h_prev, self.W_hc) + # 候选记忆：前一时间步隐藏状态 与 输入隐藏状态的权重 进行点积运算 self.b_c # 候选记忆偏置 ) # 更新细胞状态 遗忘门乘以旧状态加上输入门乘以候选状态。 c_hat表示顶上有波浪线的细胞状态 # f的形状(1, 64) c_prev的形状(1, 64) c_next = f * c_prev + i * c_hat # * 表示逐元素乘法，np.dot表示矩阵乘法 # 输出门计算 o = self.sigmoid( np.dot(x, self.W_xo) + # 输出门：输入数据与输入数据的权重进行点积运算 np.dot(h_prev, self.W_ho) + # 输出门：前一时间步隐藏状态 与 输入隐藏状态的权重 进行点积运算 self.b_o # 输出门的偏置 ) # 计算新隐藏状态 逐元素乘法 h_next = o * self.tanh(c_next) return h_next, c_next # 示例使用 if __name__ == "__main__": # 参数设置 input_size = 32 # 输入特征维度 词向量的维度 hidden_size = 64 # 隐藏状态的维度 batch_size = 1 # 暂时不考虑批量处理，只处理单个样本 # 初始化LSTM单元 lstm = LSTM_Cell(input_size, hidden_size) # 模拟输入数据 x = np.random.randn(batch_size, input_size) # 当前时间步输入，32维 print("当前时间步输入:", x) h_prev = np.zeros((batch_size, hidden_size)) # 初始隐藏状态，64维 print("初始隐藏状态:", h_prev) c_prev = np.zeros((batch_size, hidden_size)) # 初始细胞状态，64维 print("初始细胞状态:", c_prev) # 前向传播 h_next, c_next = lstm.forward(x, h_prev, c_prev) print("新隐藏状态形状:", h_next.shape) print("新细胞状态形状:", c_next.shape)
结果：
当前时间步输入: [[-2.45900451 -1.78357959 -0.31620146 -0.57266982 0.31719127 -0.84039654 1.22589186 0.40229642 1.45132049 -0.68954759 1.66383744 0.9408305 1.42693676 -1.11690322 0.78445898 0.32824467 -1.16595598 1.05788334 -1.15283355 0.81909814 -0.74497393 -0.71768296 -0.58238037 0.16841018 0.46329239 -1.51563115 -0.40920667 2.21266106 -0.54992637 0.33278381 -0.12644014 -1.63820021]] 初始隐藏状态: [[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]] 初始细胞状态: [[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]] x的形状 (1, 32) h_prev的形状 (1, 64) combined的形状 (1, 96) 遗忘门的值为： [[0.50982242 0.49301366 0.51475938 0.52168217 0.50804705 0.5066252 0.47087581 0.51180911 0.49649178 0.48682217 0.51278003 0.50153855 0.50305216 0.4753417 0.4997102 0.50475094 0.49540963 0.49120168 0.50375016 0.51076254 0.48318515 0.48411508 0.52395901 0.47510399 0.4796499 0.501662 0.5058271 0.47705483 0.49365067 0.50056661 0.49664496 0.50266981 0.50716177 0.50945226 0.52051423 0.52980419 0.50494791 0.48454232 0.50129862 0.5168752 0.50912308 0.48592776 0.51776957 0.51290076 0.50036016 0.50338137 0.45709544 0.48381141 0.48752491 0.50206702 0.49116828 0.48852665 0.49542844 0.49686131 0.50308613 0.49065816 0.52482549 0.51444809 0.54510514 0.51927386 0.49884994 0.47641636 0.51959703 0.52509 ]] 遗忘门的形状为： (1, 64) 新隐藏状态形状: (1, 64) 新细胞状态形状: (1, 64)
Bi-LSTM
Bi-LSTM即双向LSTM，它没有改变LSTM本身任何的内部结构，只是将LSTM应用两次且方向不同，再将两次得到的LSTM结果进行拼接作为最终输出
import torch import torch.nn as nn """ nn.LSTM类初始化主要参数解释： input_size: 输入张量x中特征维度的大小． hidden_size: 隐层张量h中特征维度的大小． num_layers: 隐含层的数量． bidirectional: 是否选择使用双向LSTM，如果为True，则使用；默认不使用． """ rnn=nn.LSTM(input_size=5,hidden_size=6,num_layers=2) """ 设定输入的张量x 第一个参数：sequence_length（输入序列的长度） 第二个参数：batch_size（批次的样本数） 第三个参数：input_size（输入张量x的维度） """ input=torch.randn(1,3,5) """ 设定初始化的h0,c0 第一个参数：num_layers *num_directions（层数＊网络方向数） 第二个参数：batch_size（批次的样本数） 第三个参数：hiddeh_size（隐藏层的维度） """ h0=torch.randn(2,3,6) c0=torch.randn(2,3,6) """ nn.LSTM类实例化对象主要参数解释 input: 输入张量x h0:初始化的隐层张量h. cO:初始化的细胞状态张量c. """ output,(hn,cn)=rnn(input,(h0,c0))
GRU
GRU(Gated Recurrent Unit）也称门控循环单元结构，它也是传统RNN的变体，同LSTM一样能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象．同时它的结构和计算要比LSTM 更简单。
GRU的优势：GRU和LSTM作用相同，在捕捉长序列语义关联时，能有效抑制梯度消失或爆炸，效果都优于传统rnn且计算复杂度相比lstm要小．
GRU的缺点：GRU仍然不能完全解决梯度消失问题，同时其作用RNN的变体，有着RNN结构本身的一大弊端，即不可并行计算，这在数据量和模型体量逐步增大的未来，是RNN发展的关键瓶颈
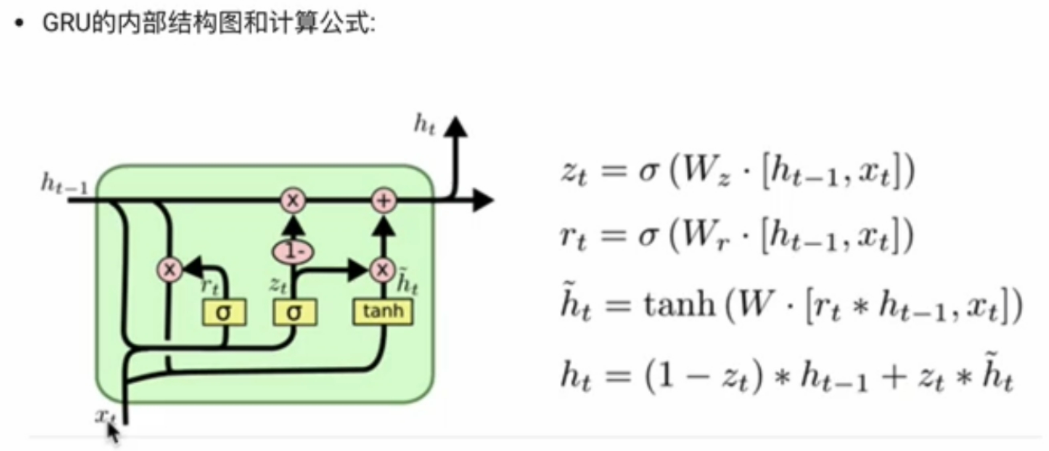
它的核心结构可以分为两个部分去解析：
更新门
重置门
import torch import torch.nn as nn """ nn.GRU类初始化主要参数解释 Input_size: 输入张量x中特征维度的大小 hidden_size:隐层张量h中特征维度的大小 num_layers:隐含层的数量 bidirectional: 是否选择使用双向LSTM，如果为True，则使用；默认不使用 """ rnn=nn.GRU(input_size=5,hidden_size=6,num_layers=2) """ 设定输入的张量x 第一个参数：sequence_length（输入序列的长度） 第二个参数：batch_size（批次的样本数） 第三个参数：input_size（输入张量x的维度） """ input=torch.randn(1,3,5) """ 设定初始化的h0 第一个参数：num_layers *num_directions（层数＊网络方向数） 第二个参数：batch_size（批次的样本数） 第三个参数：hiddeh_size（隐藏层的维度） """ h0=torch.randn(2,3,6) """ nn.GRU类实例化对象主要参数解释 input: 输入张量x. h0:初始化的隐层张量h. """ output,hn=rnn(input,h0)
六、文本生成案例（传统RNN模型训练）
文本生成任务是一种常见的自然语言处理任务，输入一个开始词能够预测出后面的词序列。本案例将会使用循环神经网络来实现周杰伦歌词生成任务。
我们收集了周杰伦从第一张专辑《Jay》到第十张专辑《跨时代》中的歌词，来训练神经网络模型，当模型训练好后，我们就可以用这个模型来创作歌词。数据集如下：
在进行自然语言处理任务之前，首要做的就是就是构建词表。
所谓的词表就是将数据进行分词，然后给每一个词分配一个唯一的编号(即索引)，便于我们送入词嵌入层获取每个词的词向量。
接下来, 我们对周杰伦歌词的数据进行处理构建词表，具体实现如下所示：
整体流程是：
⚫ 获取文本数据
⚫ 分词，并进行去重
⚫ 构建词表
if __name__ == "__main__": # 获取数据 unique_words, word_to_index, word_count, corpus_idx = build_vocab() # 数据获取实例化 dataset = LyricsDataset(corpus_idx, 32) x, y = dataset.__getitem__(0) print("网络输入值：", x) print("目标值：", y)
结果：
网络输入值： tensor([ 0, 1, 2, 3, 40, 0, 4, 5, 6, 7, 8, 3, 40, 0, 4, 5, 9, 10, 11, 3, 40, 9, 10, 7, 12, 3, 40, 13, 14, 14, 14, 10]) 目标值： tensor([ 1, 2, 3, 40, 0, 4, 5, 6, 7, 8, 3, 40, 0, 4, 5, 9, 10, 11, 3, 40, 9, 10, 7, 12, 3, 40, 13, 14, 14, 14, 10, 15])
我们用于实现《歌词生成》的网络模型，主要包含了三个层:
1. 词嵌入层: 用于将语料转换为词向量
2. 循环网络层: 提取句子语义
3. 全连接层: 输出对词典中每个词的预测概率
前面的准备工作完成之后, 我们就可以编写训练函数。训练函数主要负责编写数据迭代、送入网络、计算损失、反向传播、更新参数，其流程基本较为固定。
训练完成之后，我们使用 torch.save 方法将模型持久化存储。
从磁盘加载训练好的模型，进行预测。预测函数，输入第一个指定的词，我们将该词输入网路，预测出下一个词，再将预测的出的词再次送入网络，预测出下一个词，以此类推，直到预测出我们指定长度的内容
# 1.导入依赖包 import torch import jieba from torch.utils.data import DataLoader import torch.nn as nn import torch.optim as optim import time # 2.获取数据集并构建词表 def build_vocab(): # 数据集位置 file_name = 'data/jaychou_lyrics.txt' # 分词结果存储位置 unique_words = [] # 去重的 all_words = [] # 所有的 # 遍历数据集中的每一行文本 for line in open(file_name, 'r',encoding='utf-8'): # 使用jieba精确模式分词,分割结果是一个列表 words = jieba.lcut(line) # print(words) # 所有的分词结果存储到all_words，其中包含重复的词组 all_words.append(words) # 遍历分词结果，去重后存储到unique_words for word in words: if word not in unique_words: unique_words.append(word) # 语料中词的数量 word_count = len(unique_words) # 词到索引映射 word_to_index = {word: idx for idx, word in enumerate(unique_words)} # 词表索引表示 corpus_idx = [] # 遍历每一行的分词结果 for words in all_words: temp = [] # 获取每一行的词，并获取相应的索引 for word in words: temp.append(word_to_index[word]) # 在每行词之间添加空格隔开 temp.append(word_to_index[' ']) # 获取当前文档中每个词对应的索引 corpus_idx.extend(temp) return unique_words, word_to_index, word_count, corpus_idx # 3.构建数据集对象 class LyricsDataset(torch.utils.data.Dataset): def __init__(self, corpus_idx, num_chars): # 文档数据中词的索引 self.corpus_idx = corpus_idx # 每个句子中词的个数，每一个批次batch_size相当于一个句子 self.num_chars = num_chars # num_chars值为32 # 词的数量 self.word_count = len(self.corpus_idx) # 句子数量 word_count必须大于num_chars, 否则number值为0 self.number = self.word_count // self.num_chars # // 表示取整除，返回除法的整数部分，9//2结果为4 def __len__(self): # 返回句子数量 return self.number def __getitem__(self, idx): # idx指词的索引，并将其修正索引值到文档的范围里面 start = min(max(idx, 0), self.word_count - self.num_chars - 2) # 输入值 x = self.corpus_idx[start: start + self.num_chars] # 网络预测结果（目标值） y = self.corpus_idx[start + 1: start + 1 + self.num_chars] # y的值为x的值往后移动一位 # 返回结果 return torch.tensor(x), torch.tensor(y) # 4.模型构建 class TextGenerator(nn.Module): def __init__(self, word_count): super(TextGenerator, self).__init__() # 初始化词嵌入层Embedding: 参数一为词的数量，参数2为词向量的维度128，返回结果ebd为[5703,128]的矩阵 # 参数word_count是词汇表的大小，也就是嵌入层的输入维度。嵌入层的输出维度是128，这可能是将每个单词映射到128维的向量。 self.ebd = nn.Embedding(word_count, 128) # 嵌入层到隐藏层 将5703个索引全部表示成向量 # 循环网络层RNN（单层单向RNN）: 词向量维度 128, 隐藏状态的维度 128, 网络层数1（默认为1层） self.rnn = nn.RNN(128, 128, 1) # 隐藏层到隐藏层 输入和隐藏层都是128，RNN层数是1。 # 输出层Linear: 将RNN的输出转换为word_count维,特征向量维度128与隐藏向量维度相同,参数2为词表中词的个数 self.out = nn.Linear(128, word_count) # 隐藏层到输出 nn.Linear()线性层（全连接层） def forward(self, inputs, hidden): # inputs的形状为 (1,32)，输出维度: (batch, seq_len,词向量维度 128)即(1,32,128) 根据词的索引得到128维的词向量 embed = self.ebd(inputs) # (1,32,128) embed可以看作是32行128列的矩阵 # 修改embed维度: (seq_len, batch,词向量维度 128) 即(1,32,128)修改为(32,1,128) # 嵌入层处理后，输出的形状可能需要调整，因为PyTorch的RNN通常期望输入是(seq_len, batch_size, input_size) output, hidden = self.rnn(embed.transpose(0, 1), hidden) # hidden为隐藏状态 (1,1,128) output的形状是torch.Size([32, 1, 128]) # 输入维度: (seq_len*batch,词向量维度 ) 即reshape后形状(32,128)，通过线性层得到(32*1, word_count) 即torch.Size([32, 5703]) # 将三维输出 (seq_len, batch, hidden_size) 压缩为二维 (seq_len*batch, hidden_size) 便于一次性计算所有时间步的预测结果 output = self.out(output.reshape((-1, output.shape[-1]))) # reshape修改形状，行为-1时，行待定，根据列来计算。output.shape[-1]值为128 # 网络输出结果 return output, hidden def init_hidden(self, bs=1): # 这里的bs（batch_size）要与DataLoader中的batch_size值相同 # 隐藏状态的初始化:[网络层数, batch, 隐藏层向量维度] return torch.zeros(1, bs, 128) # 因为是单层单向RNN，所以第一维是1 # 5.模型训练 def train(): # 构建词典 index_to_word, word_to_index, word_count, corpus_idx = build_vocab() print("word_count的值为：", word_count) # 5703,即去重后总共有5703个词 print("corpus_idx的值为：", corpus_idx) # 数据集 lyrics = LyricsDataset(corpus_idx, 32) # 每次训练32个词 # 初始化模型 model = TextGenerator(word_count) # 指定损失函数 criterion = nn.CrossEntropyLoss() # 交叉熵损失 通常用于多分类问题 # 优化方法 optimizer = optim.Adam(model.parameters(), lr=1e-3) # 训练轮数 epoch = 10 for epoch_idx in range(epoch): # 数据加载器 lyrics_dataloader = DataLoader(lyrics, shuffle=True, batch_size=1) # 每次一个批次进行训练，batch_size参数要与init_hidden方法中的bs值相同 # 训练时间 start = time.time() iter_num = 0 # 迭代次数 # 训练损失 total_loss = 0.0 # 遍历数据集 for x, y in lyrics_dataloader: # print("x的值为：",x) # tensor([[40, 20, 13, 27, 5, 3, 40, 28, 18, 20, 13, 29, 18, 30, 31, 3, 40, 32,18, 20, 13, 33, 18, 30, 31, 3, 40, 34, 18, 20, 13, 35]]) print("y的值为：", y) # tensor([[20, 13, 27, 5, 3, 40, 28, 18, 20, 13, 29, 18, 30, 31, 3, 40, 32, 18,20, 13, 33, 18, 30, 31, 3, 40, 34, 18, 20, 13, 35, 18]]) # 隐藏状态的初始化 (1,1,128) hidden = model.init_hidden() # 模型计算 output, hidden = model(x, hidden) # output的形状为torch.Size([32, 5703]) # 计算损失 # y:[batch,seq_len]->[seq_len,batch]->[seq_len*batch] y为1维数组 # transpose将y的第0维和第1维进行交换，得到(32,1),contiguous保证转置后在内存中连续，view(-1)表示展平 y = torch.transpose(y, 0, 1).contiguous().view(-1) # y的维度由(1,32)变为(32,)，即展平后 # 在PyTorch中，当使用交叉熵损失函数nn.CrossEntropyLoss时，输入output的形状为[batch_size, num_classes] # （例如[32, 5703]），而目标y的形状为[batch_size]（例如(32,)）是完全正确且允许的 loss = criterion(output, y) # 计算损失 optimizer.zero_grad() # 梯度清零 loss.backward() # 自动微分 optimizer.step() # 参数更新 iter_num += 1 # 迭代次数加1 total_loss += loss.item() # 打印训练信息 print('epoch %3s loss: %.5f time %.2f' % (epoch_idx + 1, total_loss / iter_num, time.time() - start)) # 模型存储 torch.save(model.state_dict(), 'data/lyrics_model_%d.pth' % epoch) # 6.模型预测 def predict(start_word, sentence_length): # 构建词典 index_to_word, word_to_index, word_count, _ = build_vocab() # 构建模型 model = TextGenerator(word_count) # 加载参数 model.load_state_dict(torch.load('data/lyrics_model_10.pth')) # 隐藏状态 hidden = model.init_hidden(bs=1) # 将起始词转换为索引 word_idx = word_to_index[start_word] # 产生的词的索引存放位置 generate_sentence = [word_idx] temp_pre = [] # 遍历到句子长度，获取每一个词 for _ in range(sentence_length): # 模型预测 output, hidden = model(torch.tensor([[word_idx]]), hidden) # 获取预测结果 word_idx = torch.argmax(output) generate_sentence.append(word_idx) # 根据产生的索引获取对应的词，并进行打印 for idx in generate_sentence: if index_to_word[idx] != ' ': print(index_to_word[idx], end='') if __name__ == "__main__": # 获取数据 unique_words, word_to_index, word_count, corpus_idx = build_vocab() # print("词的数量：\n", word_count) # print("去重后的词:\n", unique_words) # print("每个词的索引：\n", word_to_index) # print("当前文档中每个词对应的索引：\n", corpus_idx) # 数据获取实例化 # dataset = LyricsDataset(corpus_idx, 5) # 第二个参数表示每次取几个数来训练， # x, y = dataset.__getitem__(0) # print("网络输入值：", x) # print("目标值：", y) # 模型训练 train() # 模型预测 # predict("分手", 50)
关于代码中两个疑问的解释：
（1）、RNN层返回的output和输出层返回的output有什么区别？
在PyTorch中，RNN层处理输入序列后会返回两个结果：输出序列和最终的隐藏状态。这里的输出序列是每个时间步的隐藏状态，而最终的隐藏状态通常是最后一个时间步的状态。接下来，输出层（通常是Linear层）会将RNN的输出转换为词汇表大小的logits，用于预测下一个单词的概率。
RNN层返回的output的实际内容：
# 示例输出（简化） [ [ [0.2, -0.3, ..., 0.8] ], # 时间步1的隐藏状态 [ [0.5, 0.1, ..., -0.2] ], # 时间步2的隐藏状态 ... # 共32个时间步 ]
RNN层的output是每个时间步的隐藏状态，形状为(seq_len, batch_size, hidden_size)。例如，如果输入序列长度是32，批次大小是1，隐藏层大小是128，那么RNN的output形状就是(32, 1, 128)。这个output包含了每个时间步的中间表示，但还没有映射到词汇表空间。
然后，这个output被重塑为(-1, 128)，也就是(32*1, 128)，再通过Linear层，将每个时间步的隐藏状态转换为词汇表大小的向量，形状变为(32, word_count)。这个输出层的作用是将RNN的隐藏状态转换为每个单词的得分，用于后续的Softmax计算，生成概率分布。
输出层返回的output的实际内容：
# 示例输出（简化） [ [3.1, -0.5, ..., 2.8], # 时间步1的预测（5703个分数） [1.2, 4.3, ..., -1.7], # 时间步2的预测 ... # 共32个时间步 ]
对比表格：关键差异
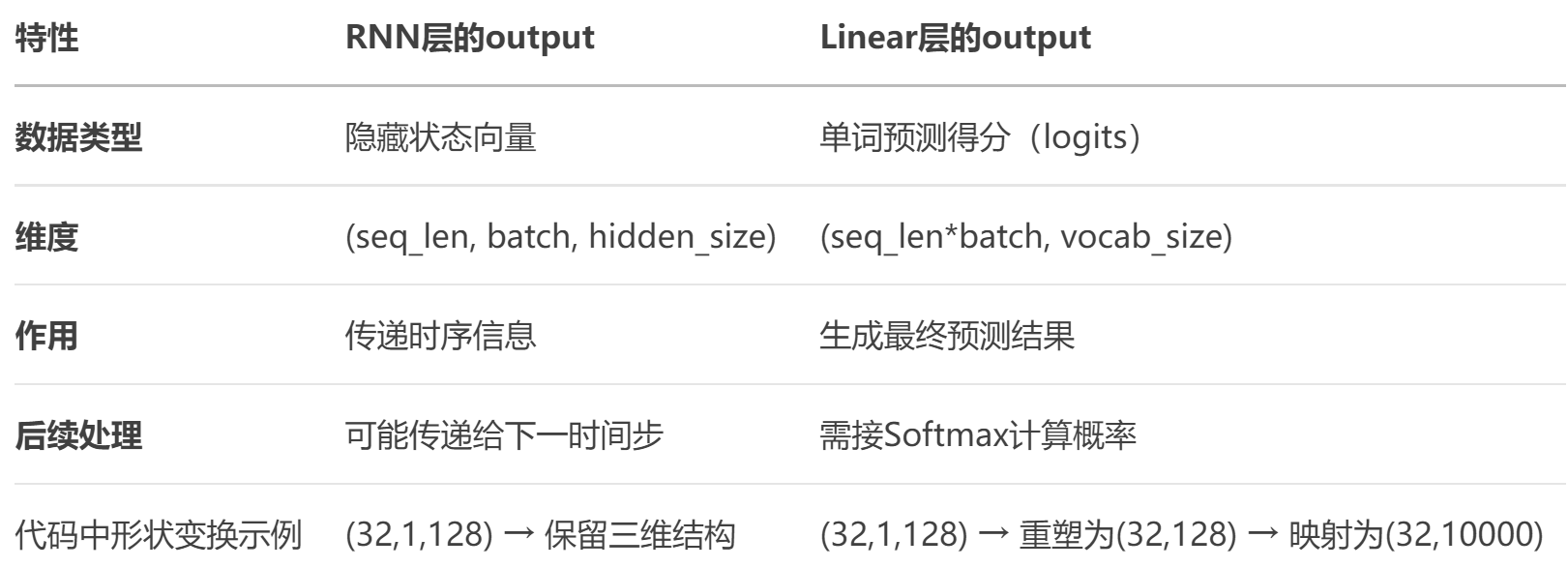
所以，两者的区别主要在于：RNN的output是中间隐藏状态，而经过Linear层后的output是预测的logits。前者用于传递序列信息，后者用于生成最终的预测结果。
（2）、loss = criterion(output, y)中，output的形状为[32, 5703]，有的形状为(32,)，形状不一样可以计算损失吗？
假设`criterion`是交叉熵损失，那么这是正确的。但如果用户错误地使用了其他损失函数，比如MSELoss，那么就会出现形状不匹配的错误。
分类任务中常用的交叉熵损失（CrossEntropyLoss）通常用于多分类问题，其中模型的输出是每个类别的得分（logits），而目标则是类别的索引。比如，如果有10个类别，每个样本的输出应该是10个分数，对应的目标是一个0到9的整数，表示正确的类别。
根据这个理解，假设现在有一个批量大小为32的样本，每个样本属于5703个类别中的一个。那么模型的输出应该是一个形状为`[32, 5703]`的张量，其中每行代表一个样本在各个类别上的得分。而目标`y`的形状为`[32,]`，这应该是一个包含32个类别索引的一维张量，每个元素的值在0到5702之间。这种情况下，交叉熵损失函数是适用的，因为它期望输入的`output`是未归一化的类别分数（即不需要提前做Softmax），而目标`y`是类别的索引。
交叉熵损失函数的设计
-
输入要求：
-
output（模型预测）：形状为(N, C)，其中：-
N 是批量大小（如32）
-
C 是类别数量（如5703）
-
-
y（真实标签）：形状为(N,)，每个元素是类别索引（0 ≤ 值 < C）
-
-
内部操作：
-
自动计算Softmax：将
output转换为概率分布（无需手动添加Softmax层）。 -
计算负对数似然：仅针对真实类别索引的位置计算损失。
-
import torch import torch.nn as nn # 模型输出 (模拟数据) output = torch.randn(32, 5703) # 形状 (32, 5703) # 目标标签 (类别索引) y = torch.randint(0, 5703, (32,)) # 形状 (32,) # 定义损失函数 criterion = nn.CrossEntropyLoss() # 计算损失 loss = criterion(output, y) # 正确执行，无报错 print(f"Loss: {loss.item()}") # Loss: 9.169746398925781
训练结果：
epoch 1 loss: 1.20117 time 11.86 epoch 2 loss: 0.15114 time 12.10 epoch 3 loss: 0.11454 time 12.74 epoch 4 loss: 0.10605 time 12.06 epoch 5 loss: 0.10517 time 11.86 epoch 6 loss: 0.10199 time 12.21 epoch 7 loss: 0.10187 time 12.04 epoch 8 loss: 0.10000 time 12.13 epoch 9 loss: 0.09930 time 13.19 epoch 10 loss: 0.09988 time 12.12
data目录下生成一个文件：
训练：
predict("分手", 50)
训练结果：
分手的话像语言暴力
我已无能为力再提起决定中断熟悉
然后在这里不限日期
然后将过去慢慢温习
让我爱上你那场悲剧
是你完美演出的一场戏
下面来详解过程：
if __name__ == "__main__": # # 获取数据 unique_words, word_to_index, word_count, corpus_idx = build_vocab() print("词的数量：\n",word_count) print("去重后的词:\n",unique_words) print("每个词的索引：\n",word_to_index) print("当前文档中每个词对应的索引：\n",corpus_idx)
结果：
部分计算过程中的数据如下：
输入值：： tensor([[ 40, 21, 165, 166, 167, 3, 168, 3, 110, 111, 112, 113, 114, 115, 40, 116, 117, 3, 118, 119, 120, 121, 40, 122, 169, 170, 171, 172, 173, 3, 116, 174]]) 输入值的形状： torch.Size([1, 32]) 词嵌入层矩阵embed的值： tensor([[[-1.2958, -0.8571, 0.7588, ..., 1.6169, 1.9001, -1.1909], [ 1.2083, 1.1077, -0.1413, ..., 1.1421, -0.5236, -0.3801], [ 0.6416, -1.2305, 1.1910, ..., -0.5675, 0.3264, 0.9053], ..., [ 1.1446, 0.9077, -2.2857, ..., -2.6371, 0.6889, 0.2578], [-0.3772, -0.3816, -1.4073, ..., -1.2335, -1.3684, 0.2937], [-0.6850, -1.0793, -0.5988, ..., -0.1137, 0.7655, -0.8379]]], grad_fn=<EmbeddingBackward0>) 词嵌入层矩阵embed的形状： torch.Size([1, 32, 128]) embed将0维和1维进行交换： tensor([[[-1.2958, -0.8571, 0.7588, ..., 1.6169, 1.9001, -1.1909]], [[ 1.2083, 1.1077, -0.1413, ..., 1.1421, -0.5236, -0.3801]], [[ 0.6416, -1.2305, 1.1910, ..., -0.5675, 0.3264, 0.9053]], ..., [[ 1.1446, 0.9077, -2.2857, ..., -2.6371, 0.6889, 0.2578]], [[-0.3772, -0.3816, -1.4073, ..., -1.2335, -1.3684, 0.2937]], [[-0.6850, -1.0793, -0.5988, ..., -0.1137, 0.7655, -0.8379]]], grad_fn=<TransposeBackward0>) embed将0维和1维进行交换后的形状： torch.Size([32, 1, 128]) 初始隐藏状态： tensor([[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]]) 输出值： tensor([[[ 0.2091, -0.9621, 0.9806, ..., -0.6044, -0.4600, -0.6606]], [[-0.9989, 0.9779, 0.6961, ..., 0.9951, -0.5488, 0.9453]], [[ 0.8430, 0.5412, 0.5054, ..., 0.9577, 0.9633, -0.9910]], ..., [[ 0.9125, -0.8044, 0.9854, ..., -0.9764, 0.9508, 0.9051]], [[ 0.0597, -0.9919, -0.7191, ..., -0.6497, 0.7912, 0.8166]], [[-0.9577, -0.6123, -0.8824, ..., -0.6498, 0.9894, -0.9816]]], grad_fn=<StackBackward0>) 输出值的形状： torch.Size([32, 1, 128]) 输出隐藏状态： tensor([[[-0.9577, -0.6123, -0.8824, -0.8995, -0.9042, 0.9565, -0.1428, 0.8860, -0.9790, -0.5727, 0.8848, -0.9723, 0.8676, -0.9920, 0.9942, -0.4067, 0.2976, 0.9262, 0.9958, -0.7777, 0.6875, 0.9094, 0.9442, 0.8156, 0.8882, -0.7055, 0.8328, 0.9794, -0.8960, 0.9520, 0.8365, 0.9902, -0.9884, -0.6683, -0.9900, -0.3490, 0.3317, -0.7963, 0.9898, -0.1095, -0.9273, 0.9403, 0.8138, -0.9996, -0.9981, 0.9091, -0.9950, 0.9775, 0.8839, 0.6337, -0.9900, 0.9259, 0.9958, -0.9880, -0.1991, -0.9736, -0.8691, -0.9824, 0.6884, 0.9963, -0.9781, -0.9977, 0.5066, 0.8653, 0.9542, 0.3206, 0.9935, -0.8806, -0.8317, 0.9829, 0.8567, 0.1660, 0.9436, -0.9307, -0.9968, 0.7471, -0.4998, -0.8250, 0.9966, -0.4278, -0.9874, 0.9742, -0.7348, 0.9426, 0.2600, 0.9742, 0.9971, -0.9781, 0.9950, -0.9975, -0.9107, 0.6990, 0.8932, -0.9287, -0.9666, -0.9602, 0.8438, 0.9092, -0.9337, 0.8918, 0.7540, 0.8076, 0.9593, 0.7303, -0.9412, 0.7812, 0.9781, -0.8584, -0.8608, 0.8855, -0.9979, 0.4226, -0.9804, -0.8692, -0.9863, -0.6048, 0.9878, 0.9840, 0.6600, 0.8601, -0.8760, -0.6801, -0.9930, -0.9635, 0.9955, -0.6498, 0.9894, -0.9816]]], grad_fn=<StackBackward0>) 输出隐藏状态的形状： torch.Size([1, 1, 128])
浙公网安备 33010602011771号