java中的初等函数

一、函数

基本初等函数：基本初等函数是指常值函数、幂函数、指数函数，对数函数、三角函数、反三角函数这六类函数。

初等函数：将由基本初等函数经过有限次加、减、乘、除四则运算和有限次复合运算所得到的能用一个解析式表示的函数,称为初等函数.

如：y= √（1+ sinx²），还有一类常见的初等函数,称为双曲函数。

基本初等函数在各自定义域中连续,根据定理 2.4.2~2.4.4就可以得到初等函数在其定义域内的区间上连续,即初等函数是其定义区间上的连续函数，

因此求初等函数在定义区间内的点的极限就变为求该点的函数值。

如果复合函数中的每一层函数都是连续函数,求极限运算可以与函数运算层层交换。

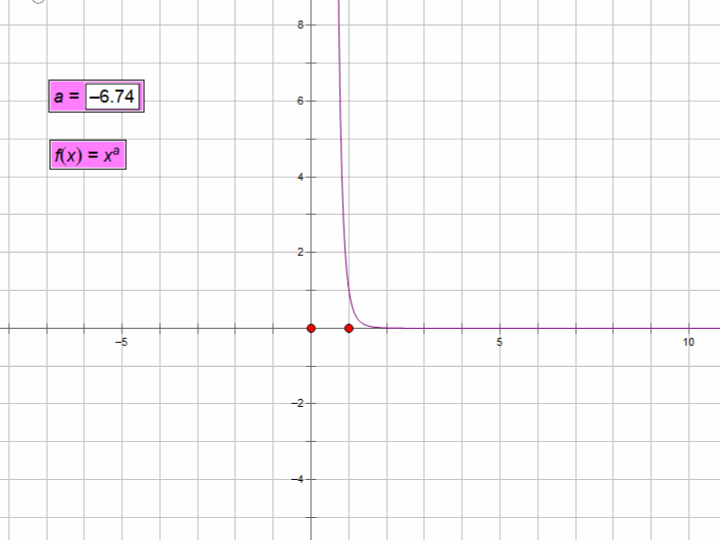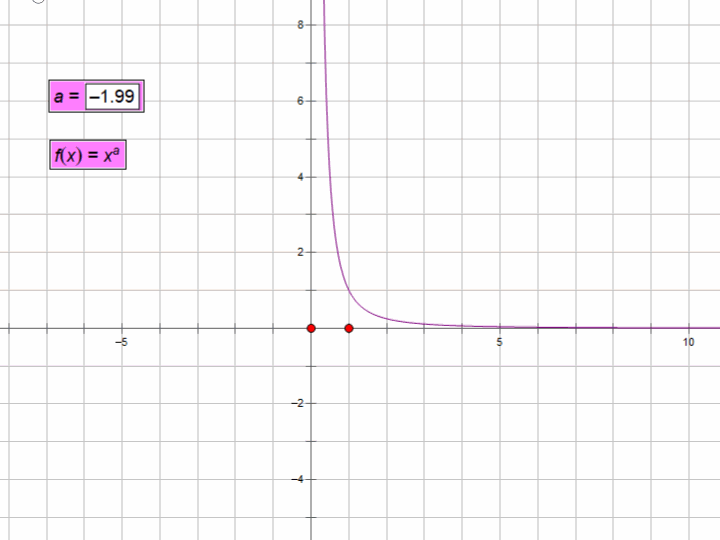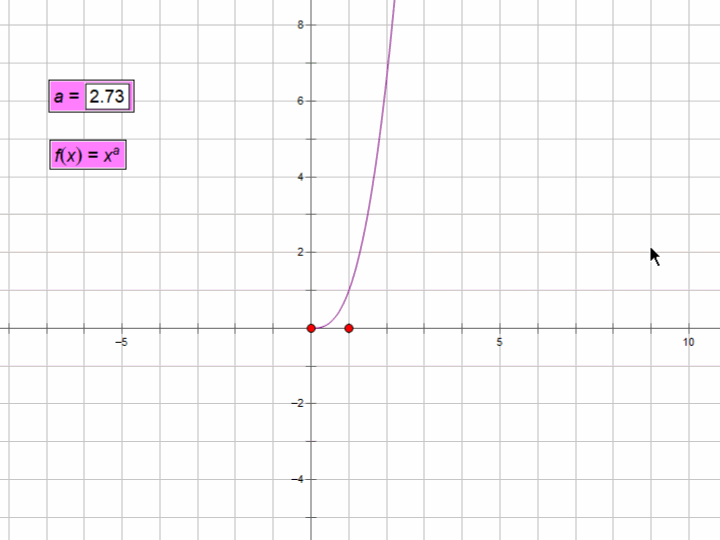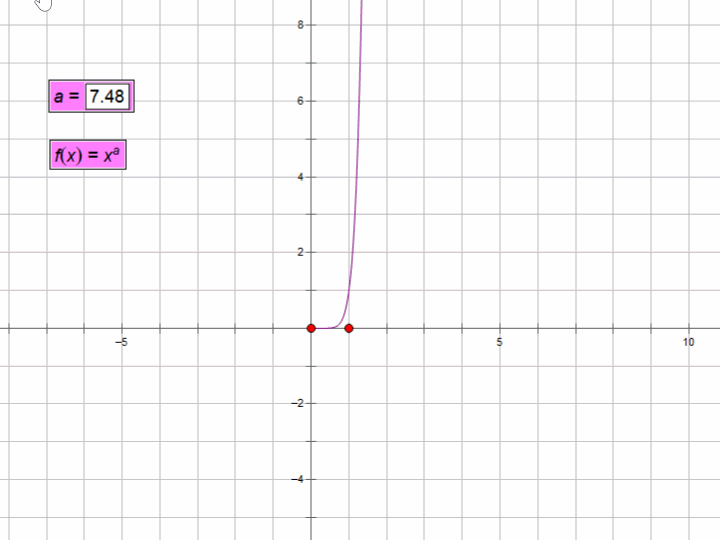
1、java的幂函数（power function）

表达式：y=x^a

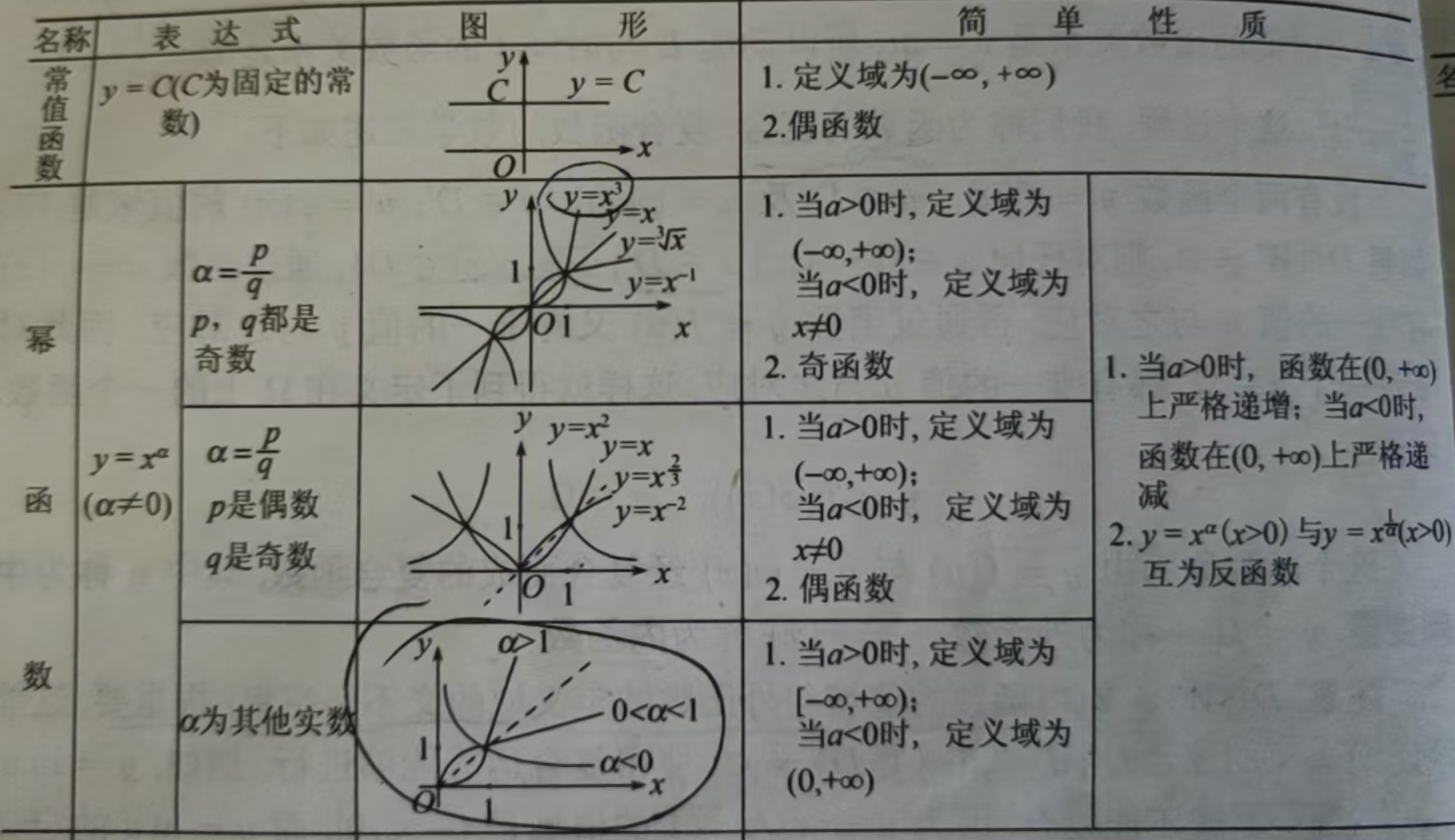
函数图像如下：

当a=-1时，y=1/x的函数图像如下：

由图可知，1/x不等于0。

double result = Math.pow(2, 3); // 8.0

您可以使用Math类的pow方法来计算以e为底的幂运算。

double result = Math.pow(Math.E, 2);
System.out.println(result);

结果为：7.3890560989306495

2、java的对数函数（log function）

表达式：y=log_a^x，（a>0，且a≠1），定义域x>0

对数函数的定义一般为：如果a（a>0，且a≠1）的b次幂等于N（N>0），a^b=N，那么数b叫做以a为底N的对数，记作logₐN=b。其中，a叫做对数的底数，N叫做真数。

通常我们将以10为底的对数叫常用对数（common logarithm），并把log10N记为lgN。另外，在科学计数中常使用以无理数e=2.71828···为底数的对数，以e为底的对数称为自然对数（natural logarithm），并且把logeN 记为ln N。

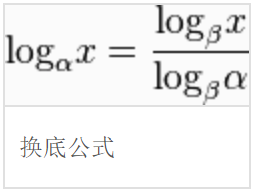
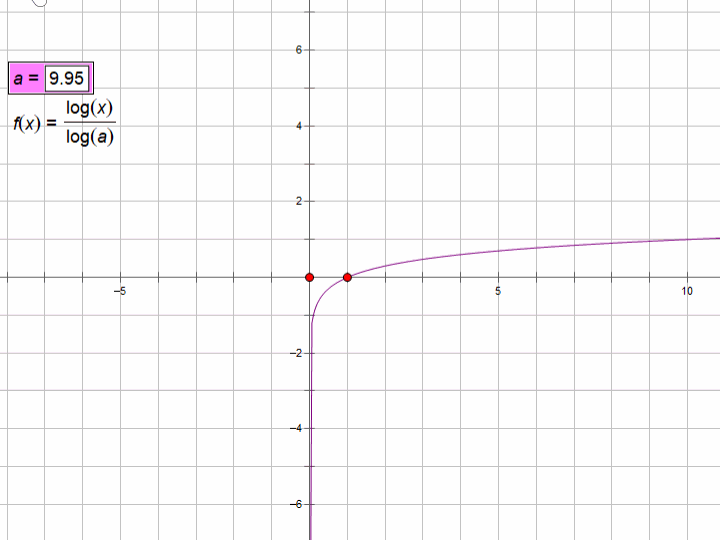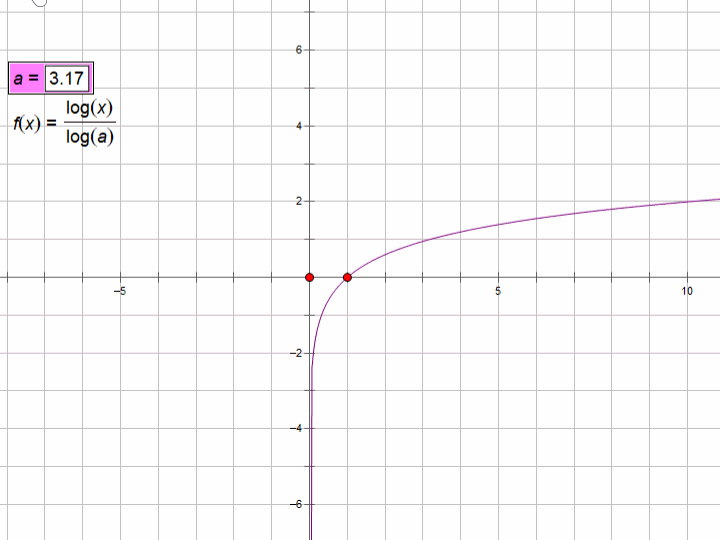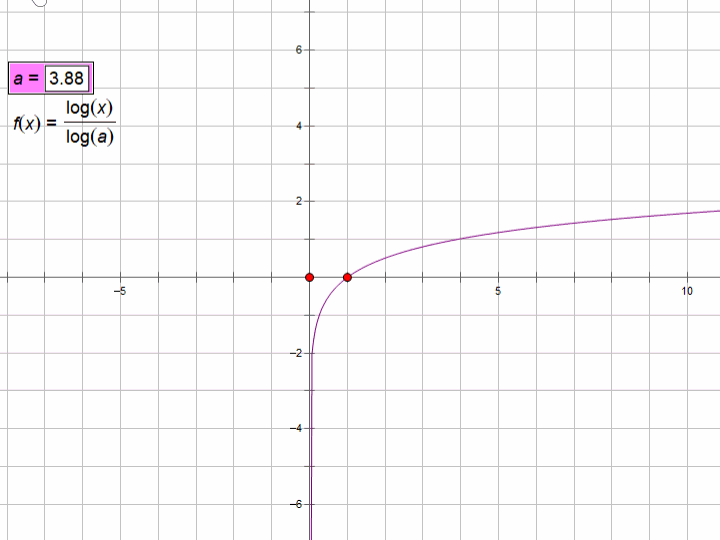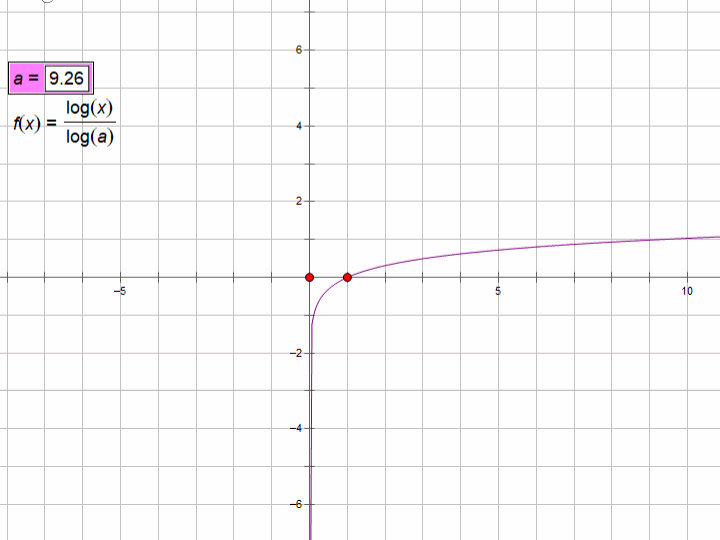
注意：几何画板中lg表示任意对数，log表示以10为底的对数。

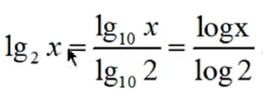
同底的对数函数与指数函数互为反函数

使用Math类的log方法可以计算以e为底的对数函数。返回 a 的自然对数，即 lna 的值，如

System.out.println("以e为底的2的对数："+Math.log(2));

结果：以e为底的2的对数：0.6931471805599453

以10为底的2的对数值

System.out.println("以10为底的2的对数值："+Math.log10(2));

结果：以e为底的2的对数：0.3010299956639812

对数的运算：

3、java的指数函数（exponential function）

指数函数的一般形式：y=a^x ，函数的定义域为R，值域为（0，+∞）

 

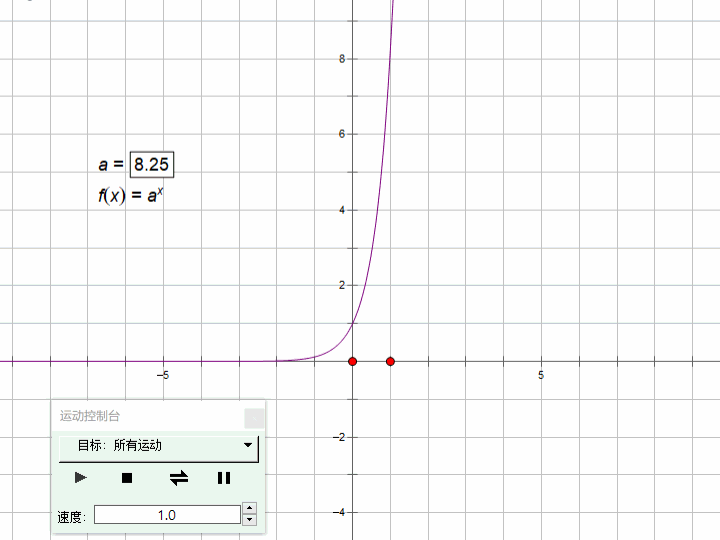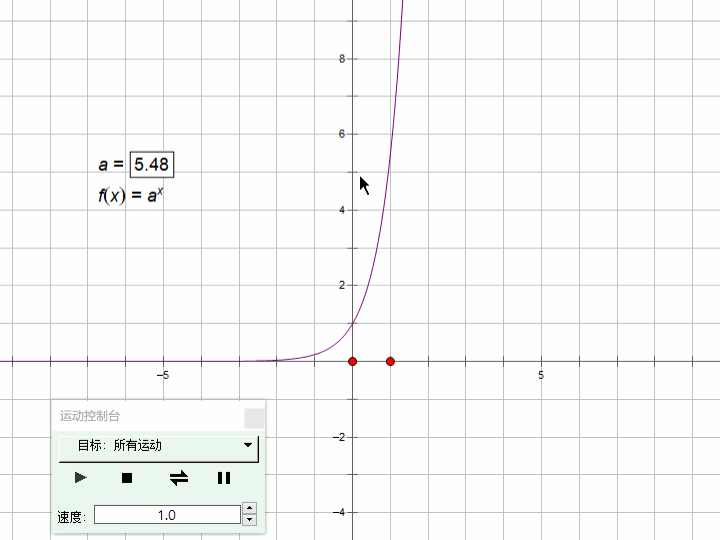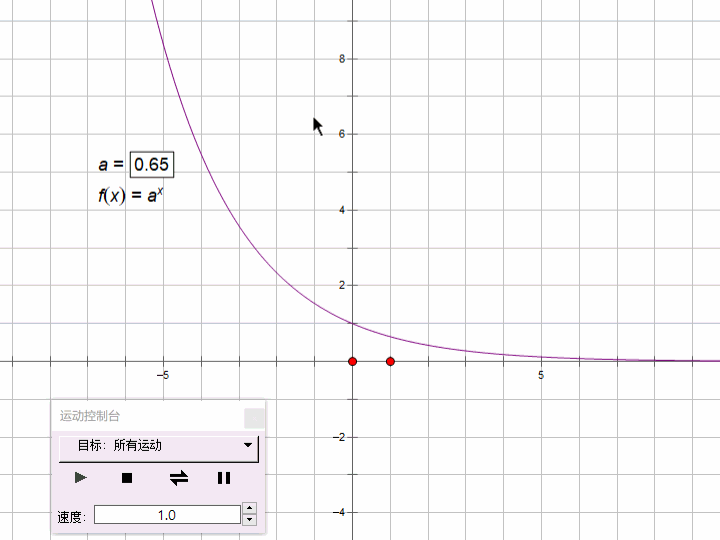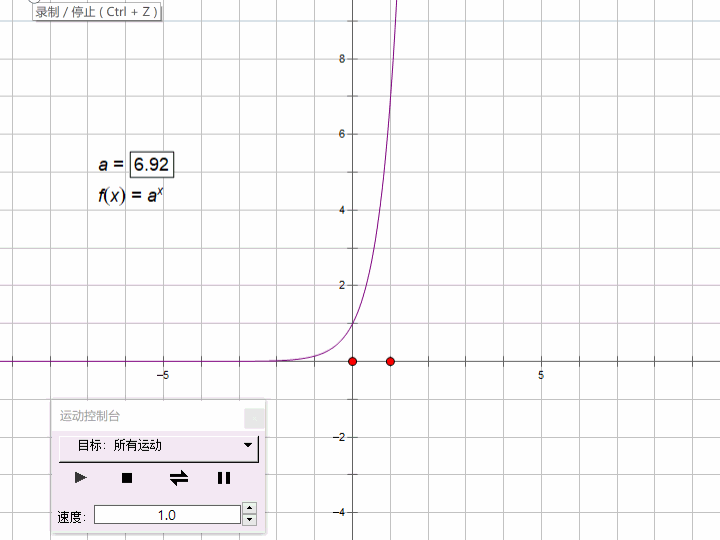
a>1时，单调递增；0<a<1时单调递减。

指数函数中a^x前面的系数为1，y=3*2^x指数函数前系数为3，故不是指数函数。

应用到值e上的这个函数写为exp(x)。还可以等价的写为ex，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。

（1）、返回以 a 为底数，以 b 为指数的幂值：

static double pow(double a,double b)

（2）、您可以使用Math类的exp方法来计算以e为底的指数函数。

System.out.println("e的平方值："+Math.exp(2));

结果为:e的平方值：7.38905609893065

（3）、返回 a 的平方根

System.out.println(Math.sqrt(4));

结果为2.0

y=√x的函数图如下：

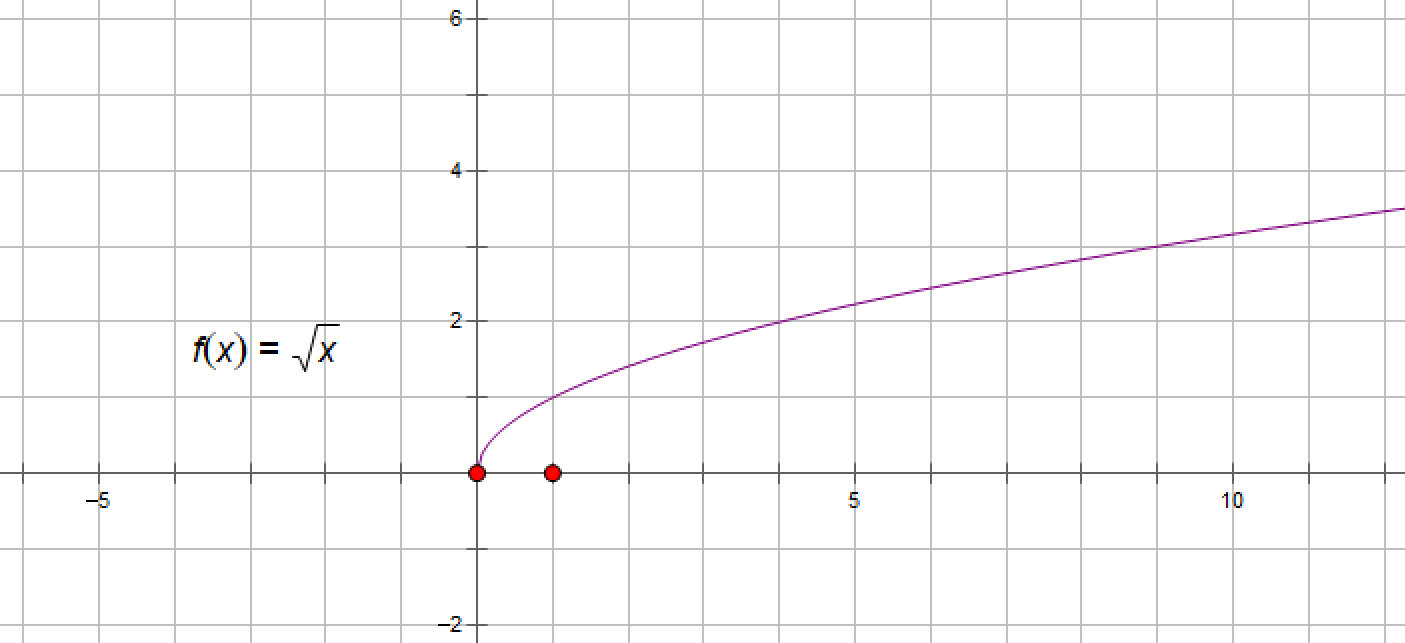
y=√x的定义域是x>=0

（4）、返回 a 的立方根

System.out.println(Math.cbrt(8));

结果为2.0

指数函数的运算法则：

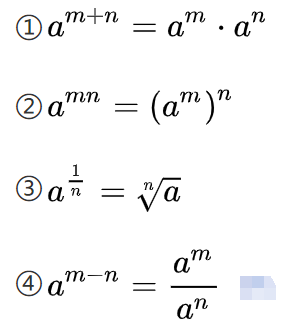
4、三角函数

（1）、正弦函数sinx

 

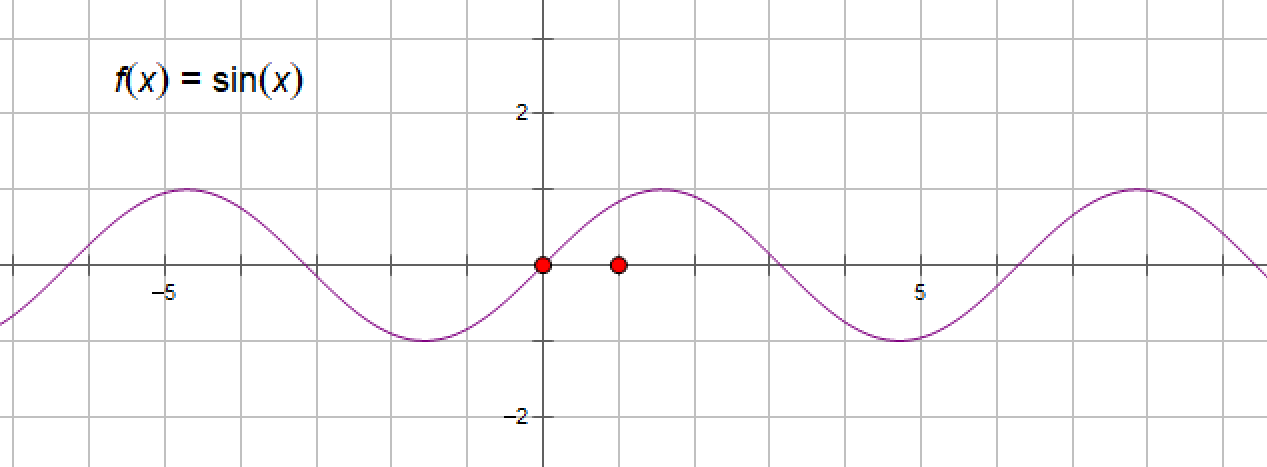
System.out.println("90度的正弦值："+Math.sin(Math.PI/2));

结果如下：90度的正弦值：1.0

正弦函数的运算公式：

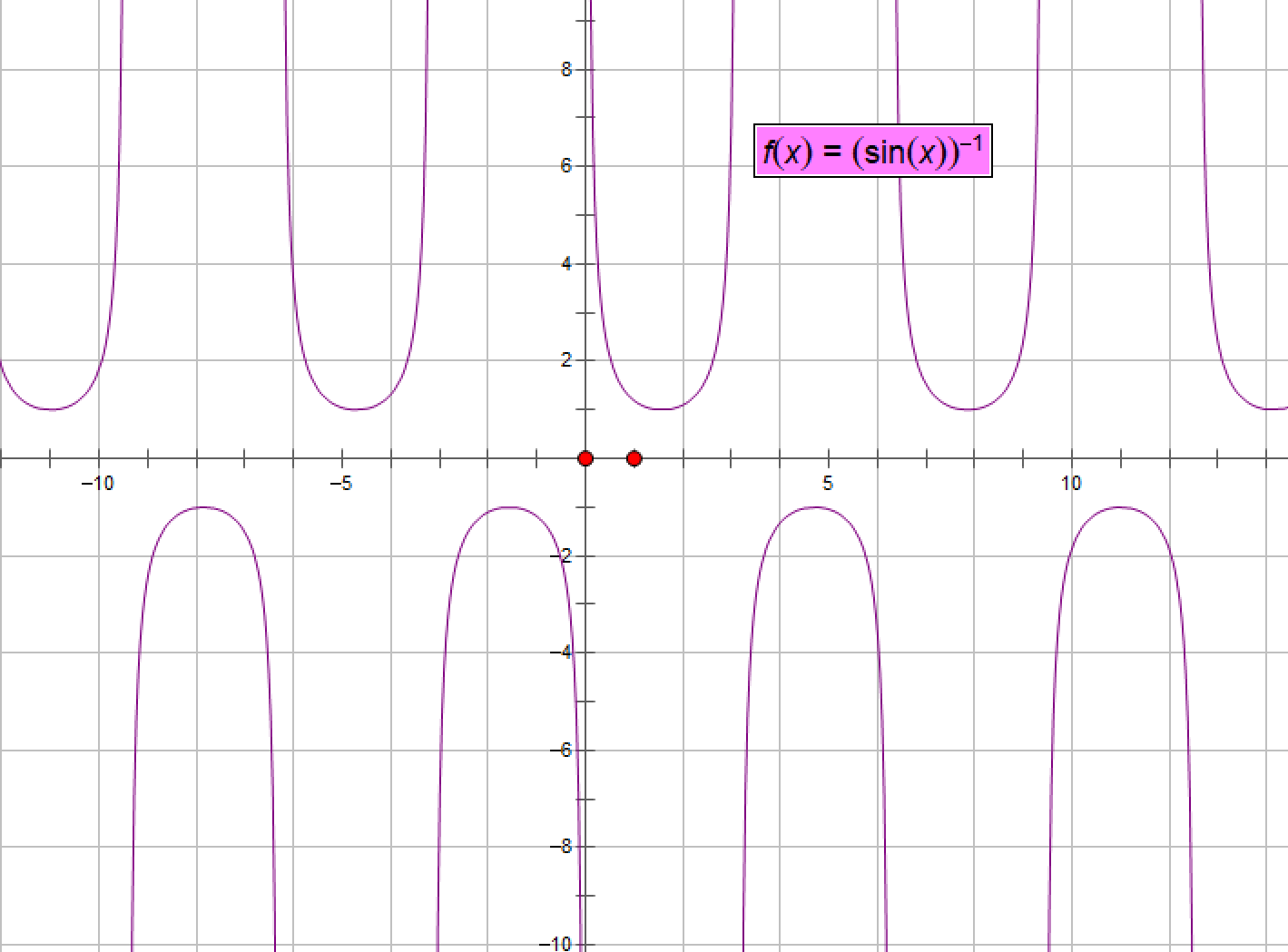
其中secα=1/cosα，cscα=1/sinα

secx函数图像：

cscx函数的图像：

（2）、余弦函数cosx

 

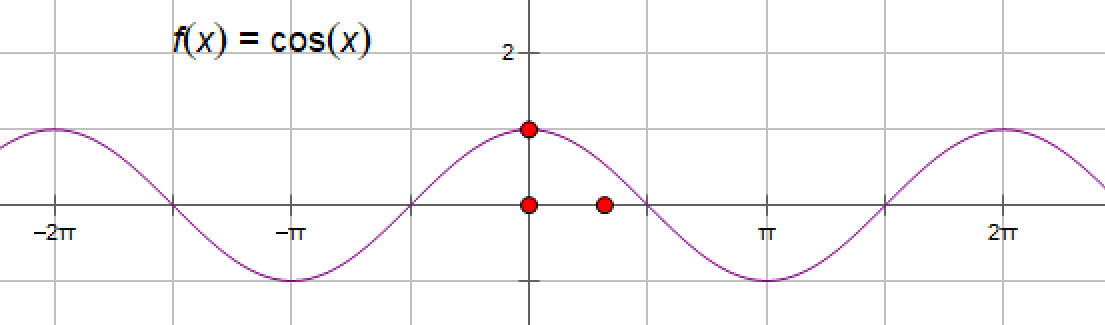
System.out.println("0度的余弦值："+Math.cos(0));

结果：0度的余弦值：1.0

余弦函数的运算：

 

（3）、反正弦函数asinx（x∈[-1,1]）

 

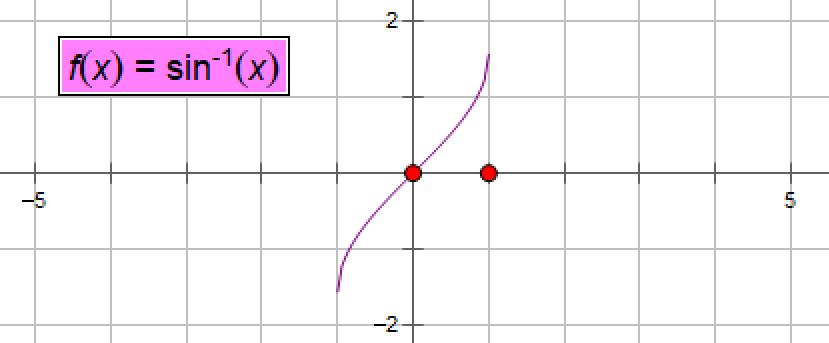
System.out.println("1的反正弦值："+Math.asin(1));

结果：0度的余弦值：1.5707963267948966

（4）、反余弦函数acosx(x∈[-1,1])

 

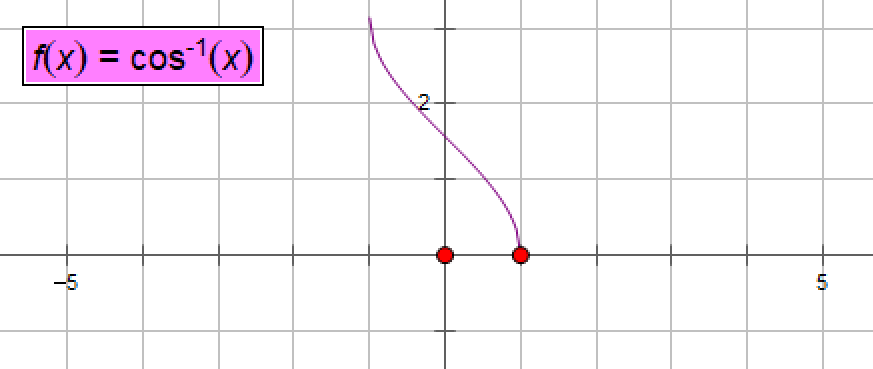
System.out.println("1的反余弦值："+Math.acos(1));

结果：1的反余弦值：0.0

（5）、正切函数tanx

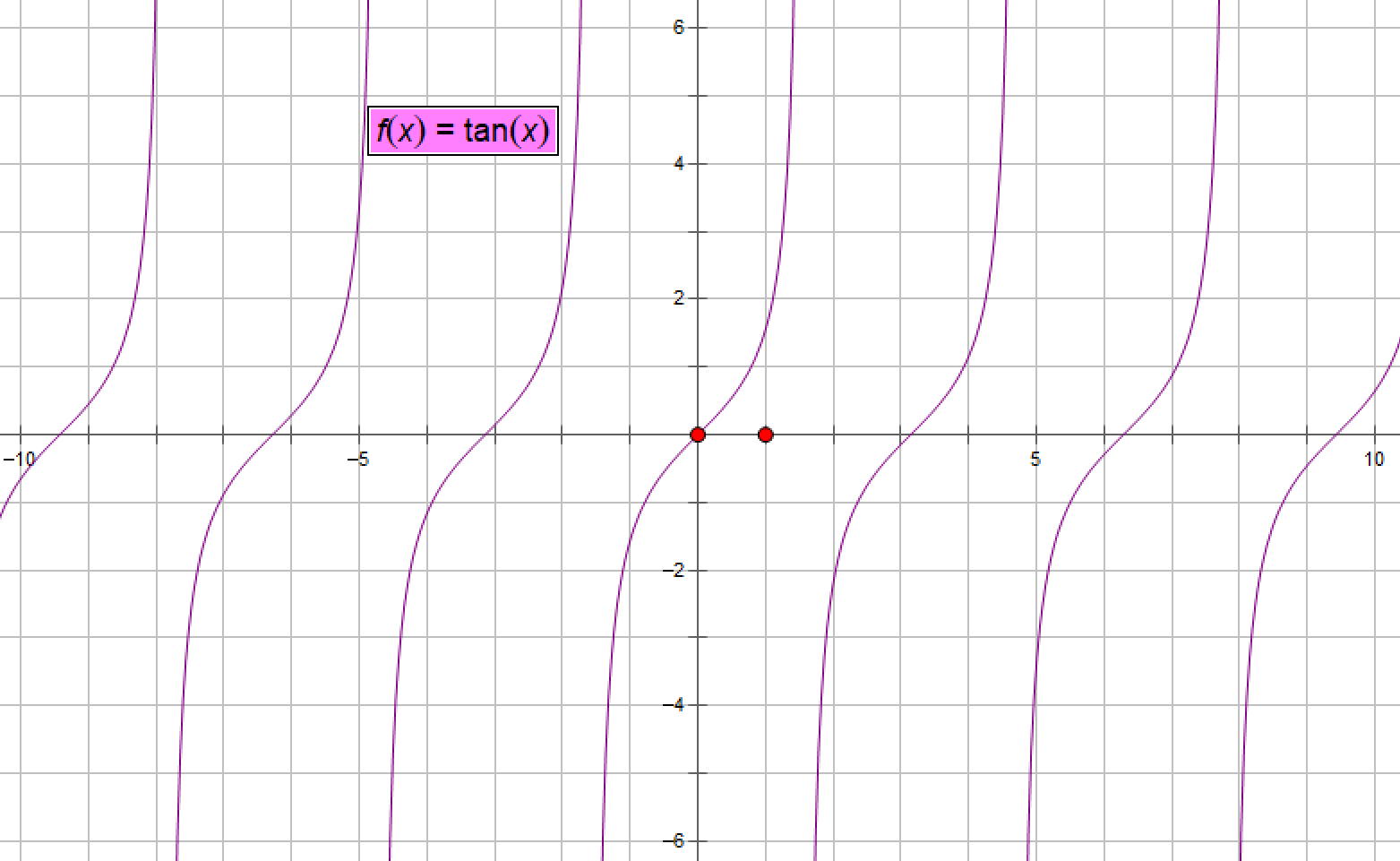
System.out.println("180度正切值："+Math.tan(Math.PI));

结果：180度正切值：-1.2246467991473532E-16（即值为0）

（6）、反正切函数atanx

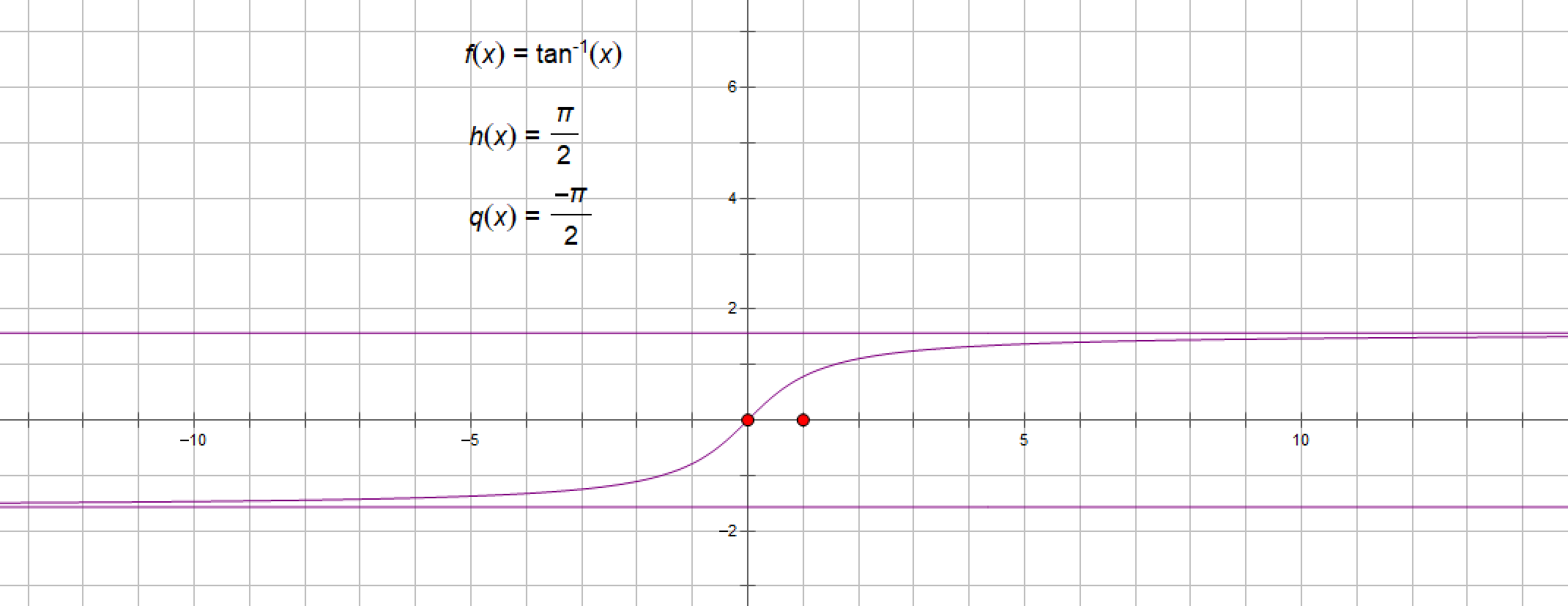
System.out.println("1的反正切值："+Math.atan(1));

结果：1的反正切值：0.7853981633974483

（7）余切函数cotx

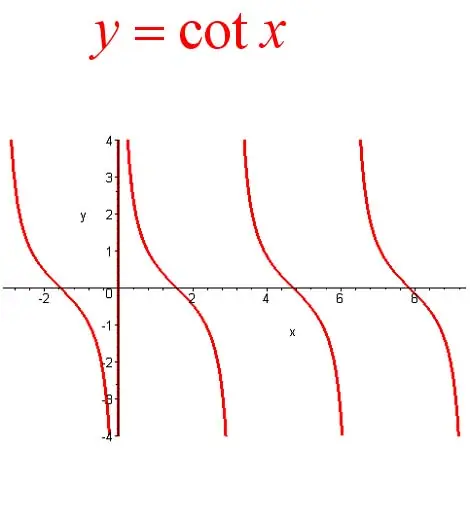
反余切函数arccotx的图像：

（8）、弧度（radian）与角度互转

System.out.println(Math.toDegrees(Math.PI));
System.out.println(Math.toRadians(90));

结果如下：

180.0
1.5707963267948966

（9）双曲正弦函数y=shx=(e^x-e^-x)/2

双曲函数是指数函数通过运算得到的。

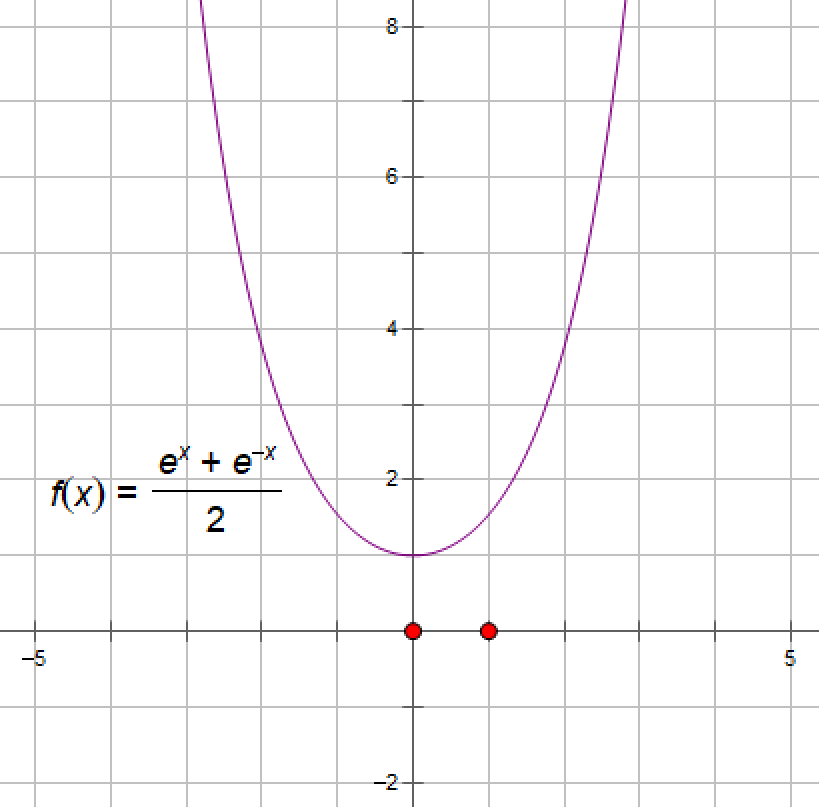
（10）双曲余弦函数y=chx=(e^x+e^-x)/2

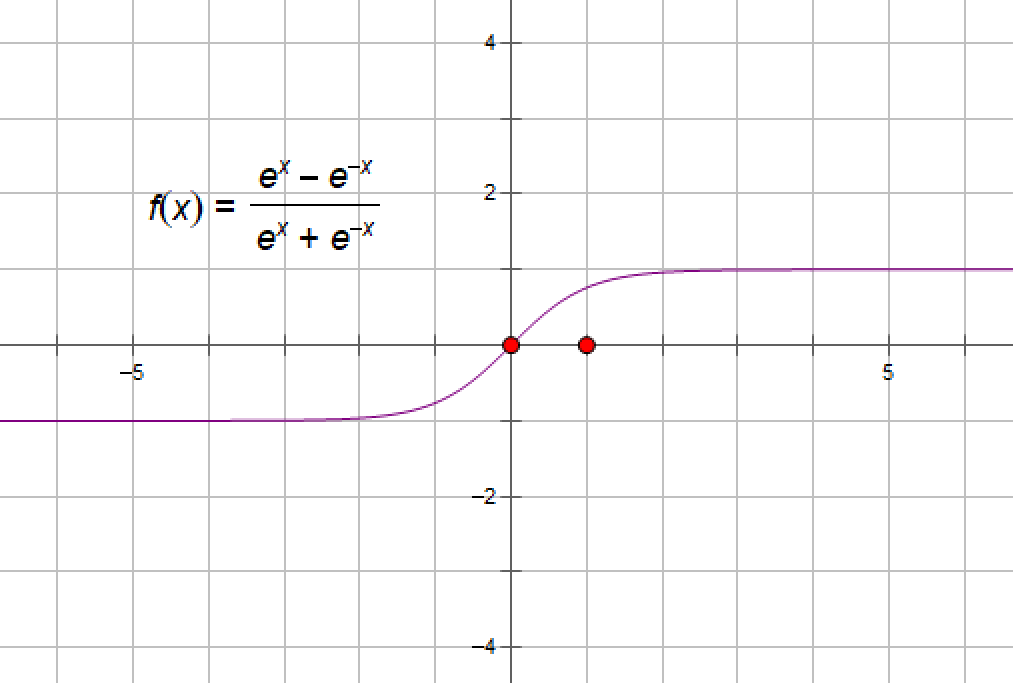
（10）双曲正切函数y=thx=(e^x-e^-x)/(e^x+e^-x)

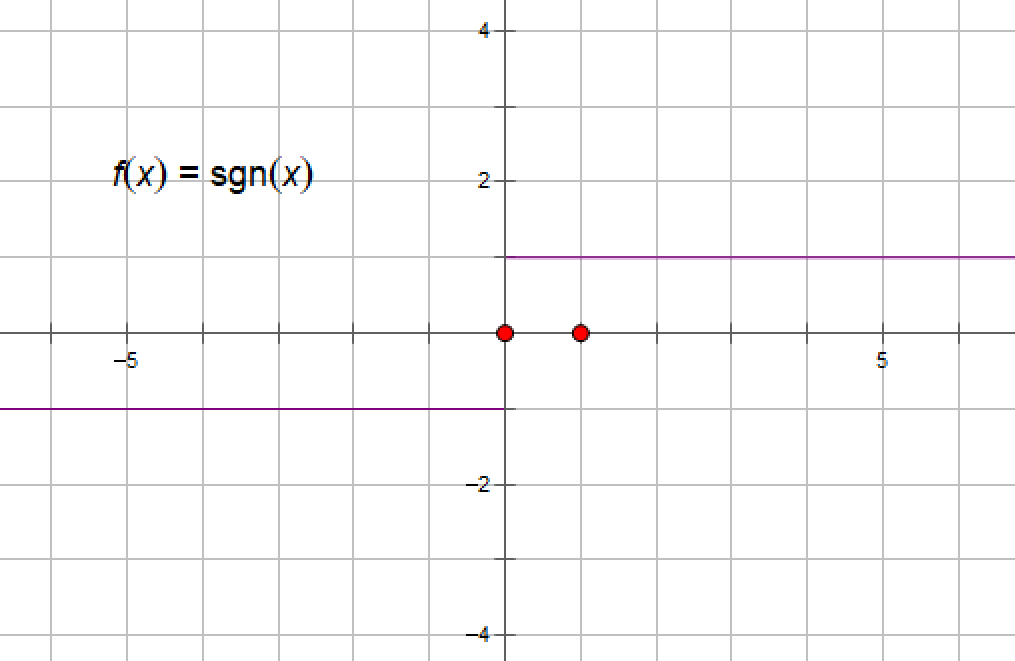
（10）符号函数y=sgnx

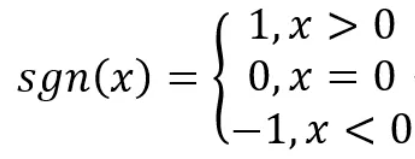
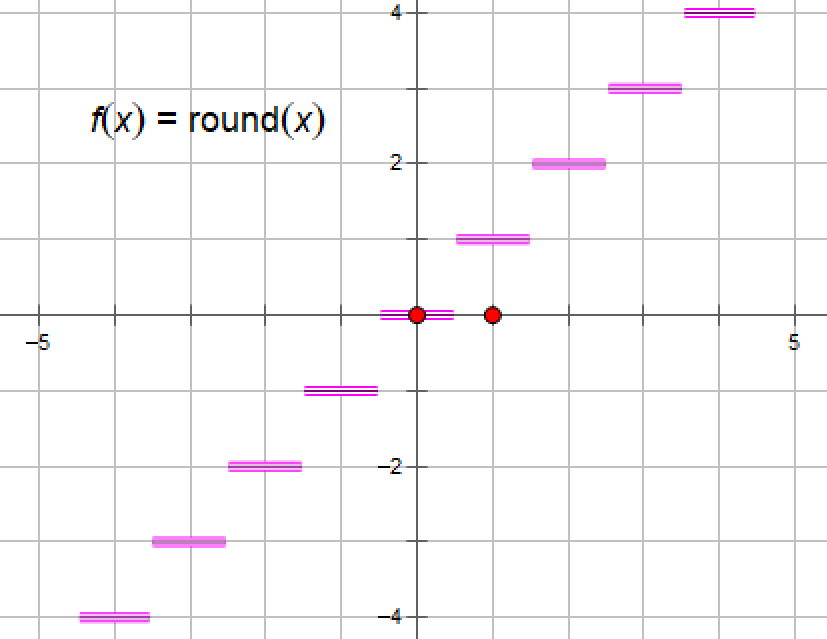
（11）四舍五入函数y=roundx

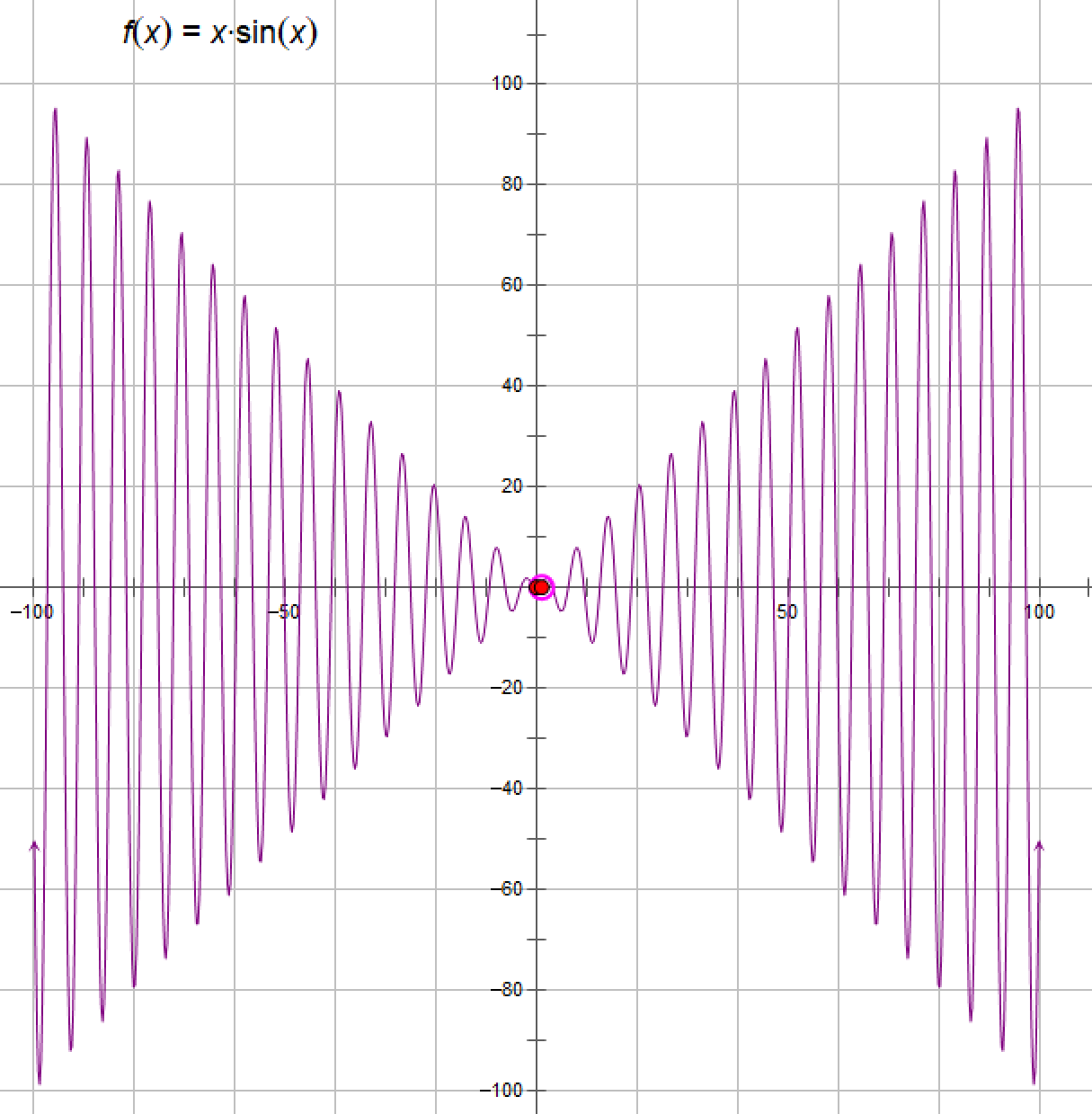
（12）函数y=xsinx

曲线

1、椭圆

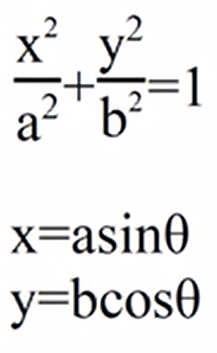
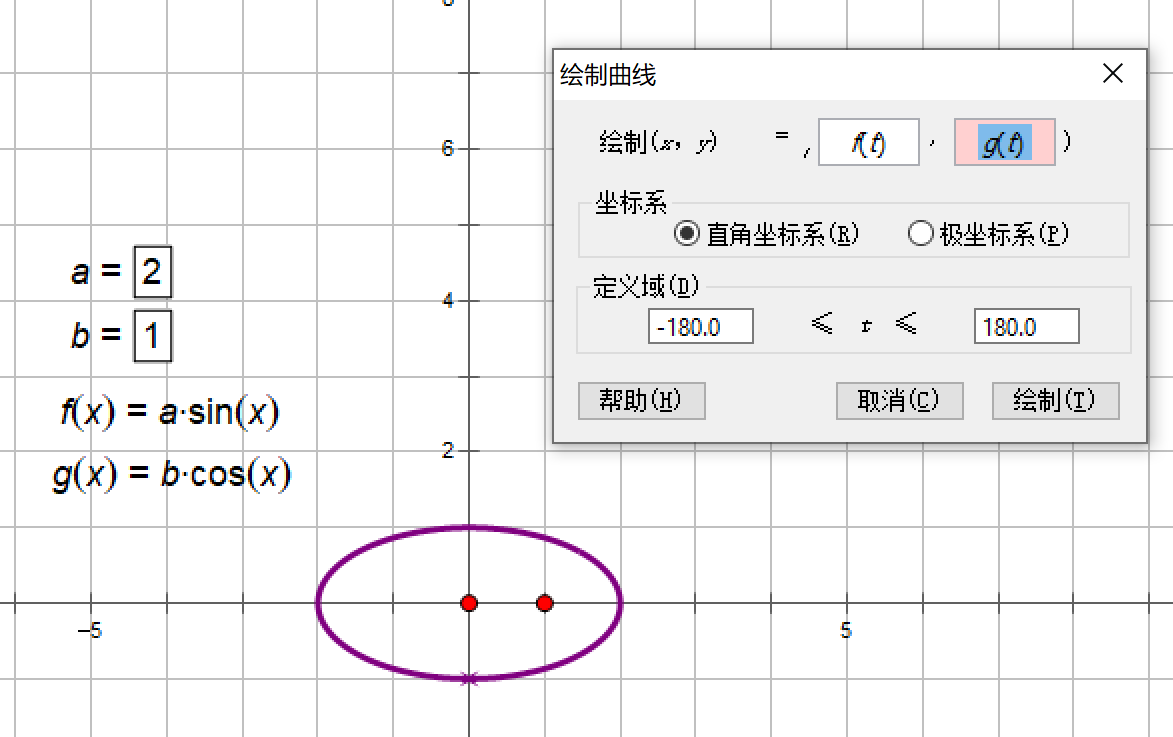
2、三叶玫瑰线r=asin3θ

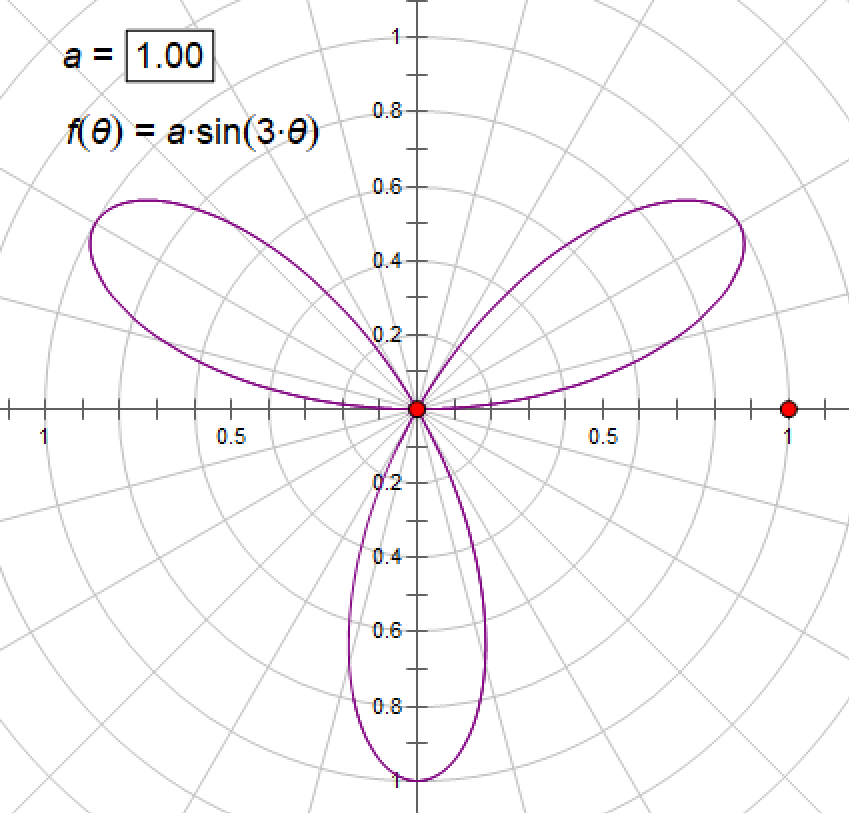
注意：用极坐标系。

 

3、阿基米德螺线r=aθ

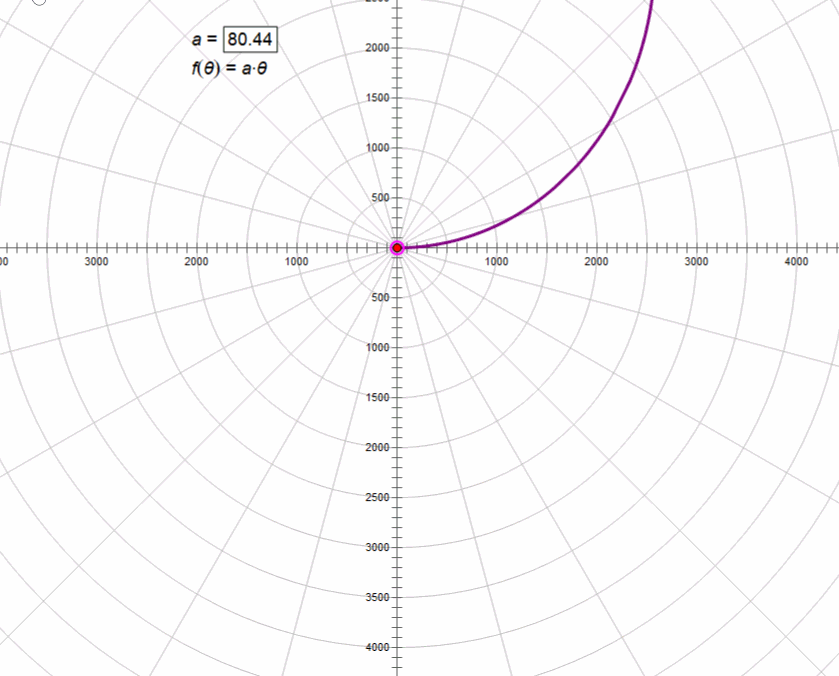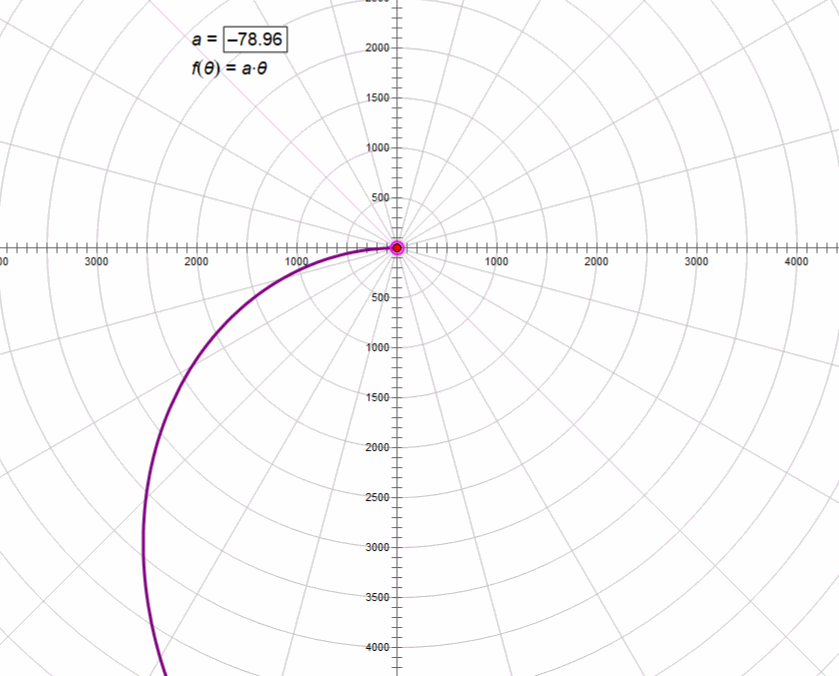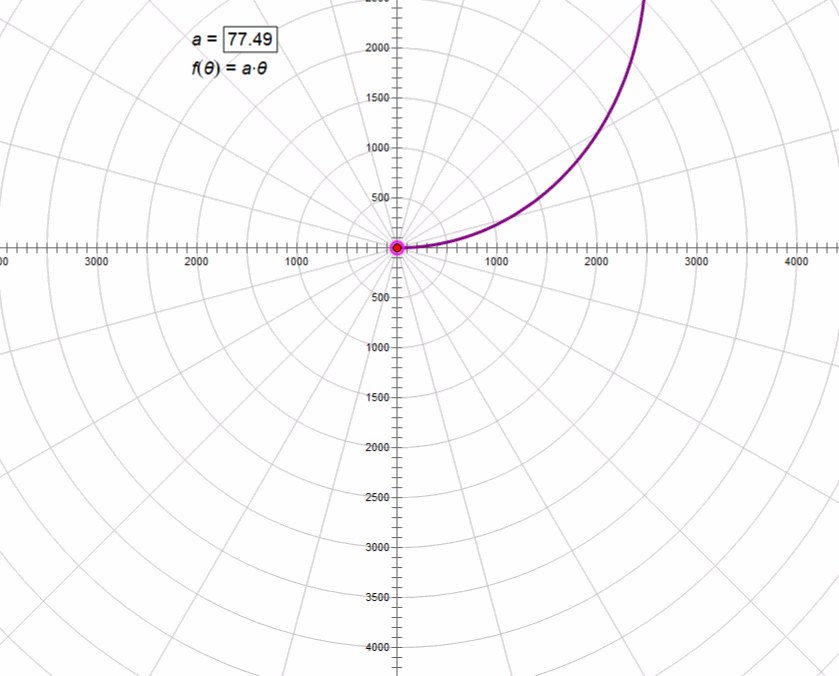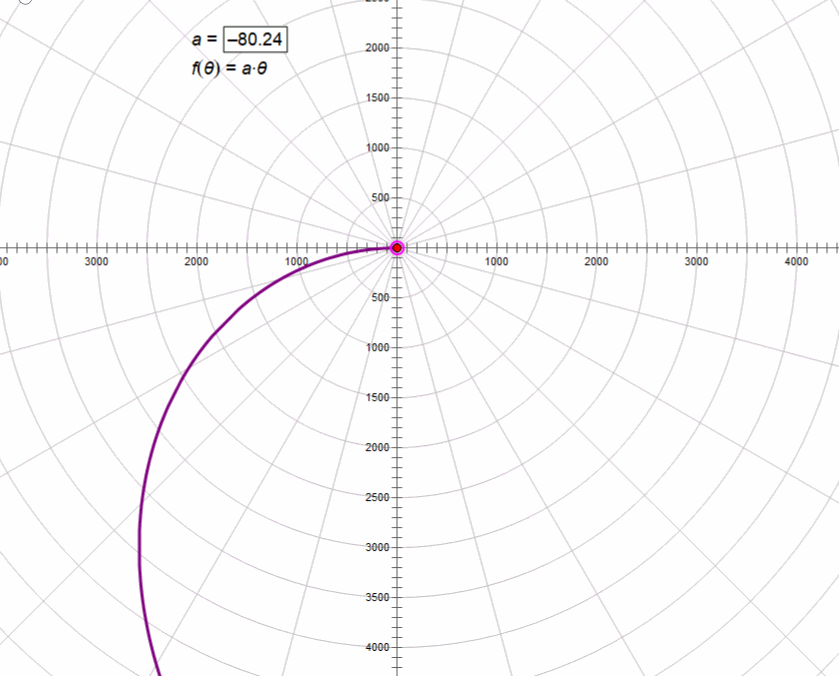
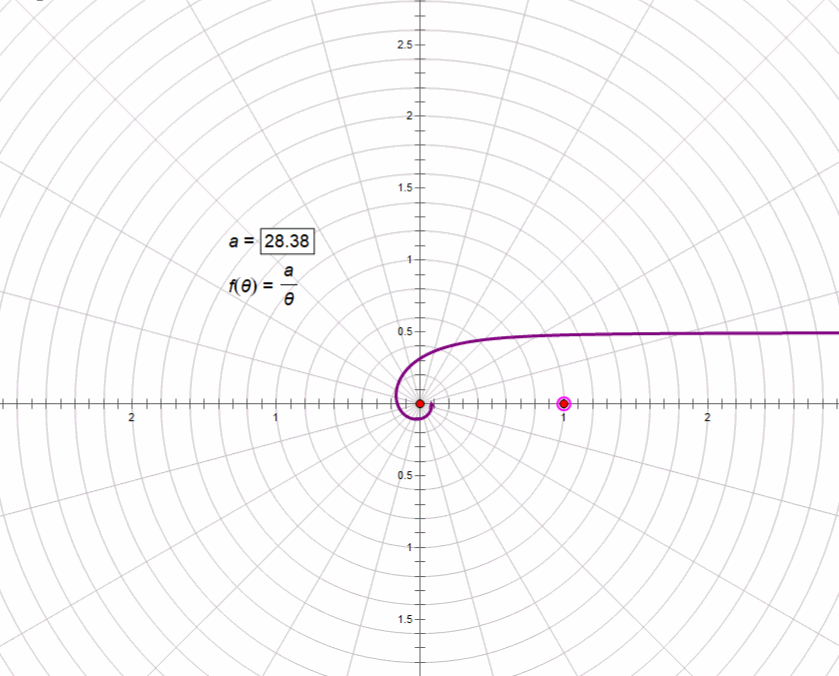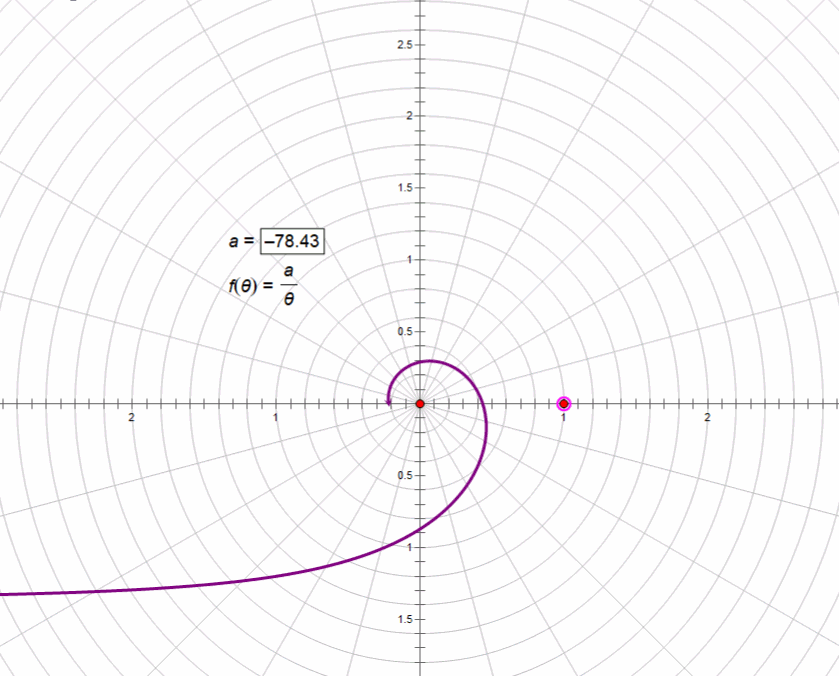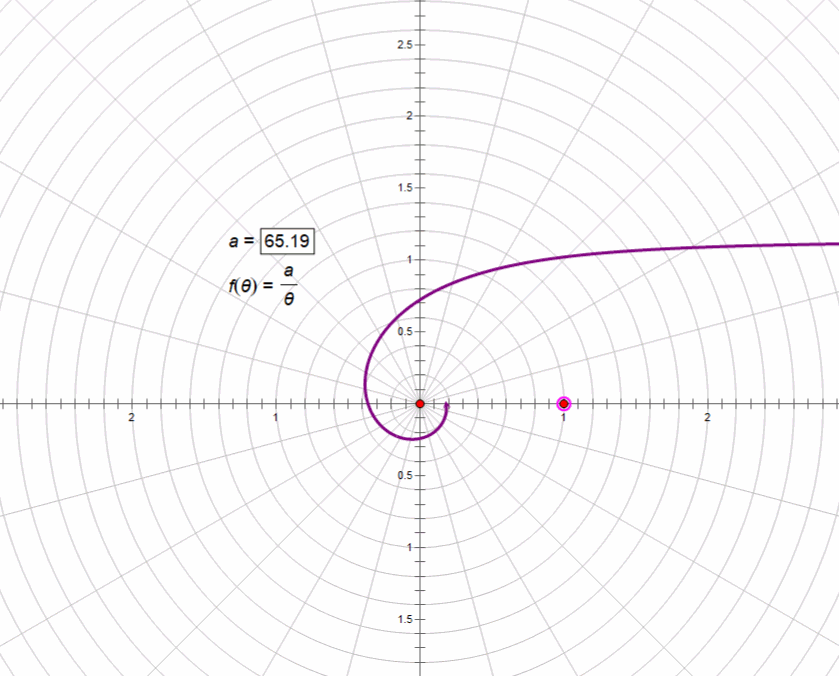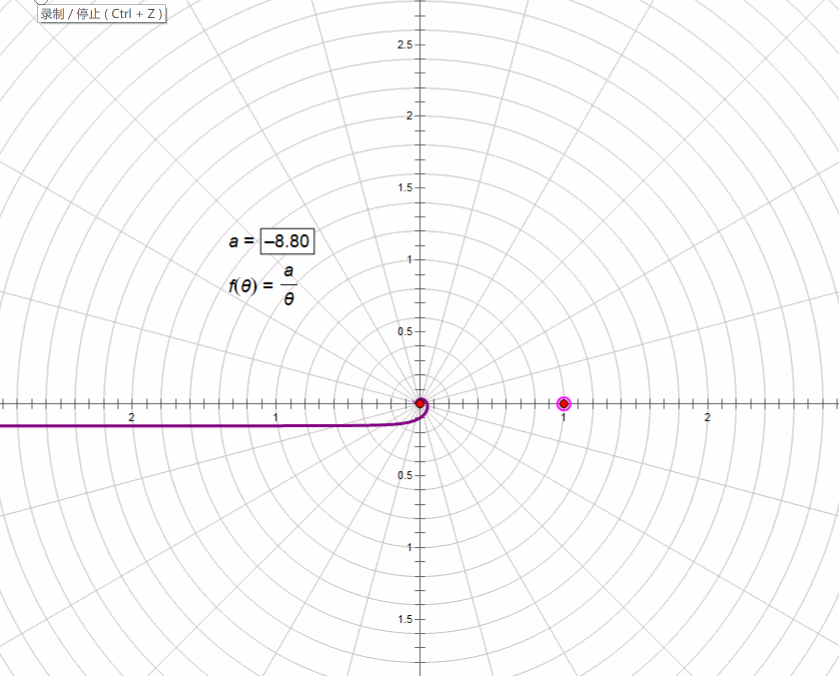
4、双曲螺线rθ=a

反函数

定义1.2.2 设函数y=f(x)在数集D上有定义,值域W=f(D).如果对任何y∈W,在D中有唯一的数x,使f(x)=y,则这个对应法则定义了在数集W上的一个函数,这个函数称为 y=f(x)在 D上的反函数,记作x = f^-1(y), y∈W.

为了与反函数相对应,将原来的函数称为直接函数.习惯上我们用x表示自变量,y表示因变量,因此,将反函数中两个变量位置互换一下,得到y= f^-1(x).除非有特别的说明,以后说函数y=f(x)的反函数就是指y= f^-1(x),反函数的定义域W=f(D),值域是 D.

反函数的图形与直接函数的图形关于直线y=x对称

二、极限

‌学习极限在数学中的作用和重要性主要体现在以下几个方面‌：

（1）、定义基本数学概念‌：极限是高等数学的基础概念，几乎所有的基本概念，如连续、导数、定积分等，都是用极限来描述的。通过极限的概念，可以定义连续性、导数、积分等重要的数学概念，为数学理论的建立和应用提供了基础‌

（2）、‌解决实际问题‌：极限在解决实际问题中有着广泛的应用。例如，通过极限的概念，可以进行近似计算和无限行为的描述，这在物理学、工程学等领域中非常重要‌

（3）、历史背景‌：极限理论的发展源于数学家们对分析的庞大分支在概念和证明中的不严密性的关注。函数概念的不清晰、级数的收敛和发散问题、导数和积分的基本概念的不明确等问题，最终导致了极限理论的出现。极限理论解决了这些问题，并为数学分析提供了坚实的基础‌

（4）、教育意义‌：学习极限有助于培养学生的逻辑思维和问题解决能力。通过学习极限，学生可以更好地理解数学中的无限概念，提高他们的数学素养和解决问题的能力‌.

1、数列的极限

定义：设有数列 {x_n},a是一个常数,如果对于任意给定的正数ε,总存在N∈N+,使得当n>N时,有|x_n - a|< ε，记作

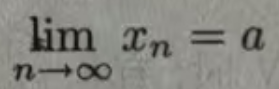
要证明数列{x_n}的极限为a，只需要证明|x_n - a|< ε时，N存在即可。

在用e-N定义证明极限时,只需要指出N存在即可,并不需要找出最小的N。通常可以适当放大|Xn-a|,使之既能小于任意正数ε(分母要有n的因子),还能够容易解出N。

数列有界是收敛的必要条件,不是充分条件,一个数列无界,它肯定发散,但发散数列未必是无界的,如{(-1)”}.

收敛与有界的关系：数列收敛，则数列有界；数列有界，不一定收敛；

发散与无界的关系：数列无界，则数列发散；数列发散，不一定无界；

要求数列的极限，既可以根据迫敛性来求证，还可以根据极限的四则运算来求。

迫敛性：

设数列{x_n)}和{_yn)的极限都是a,若数列{z_n}满足存在 N∈N*,当n>N时,有x_n≤z_n≤y_n,则

极限的四则运算：

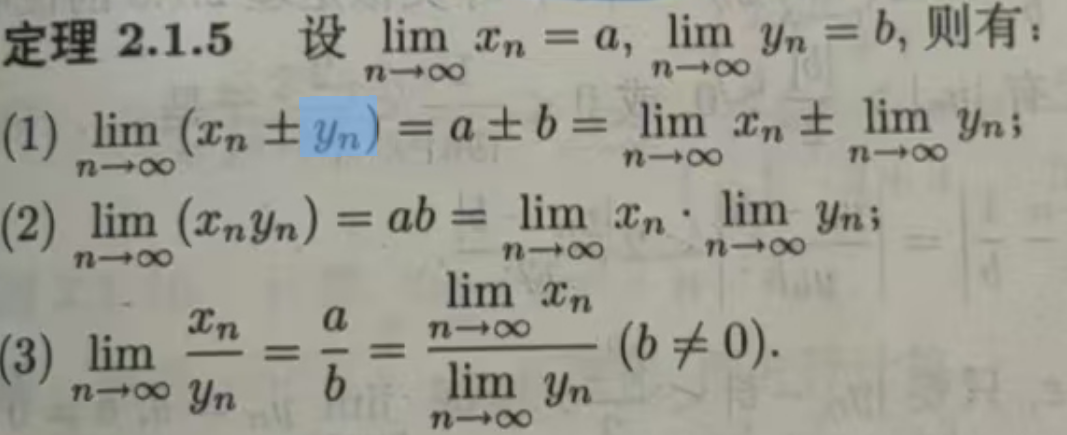
单调有界数列必有极限

单调有界是数列收敛的充分条件,但不是必要条件,其中有界是必要条件而单调性不是.

单调有界，则数列收敛；数列收敛，则有界，但不一定单调。

记住如下公式：

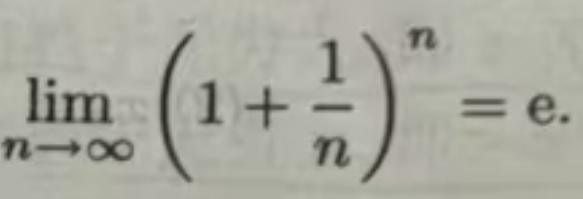
要证明N存在，需要积累一些数学公式，需要掌握以下公式：

（1）、二项式定理：

（2）、排列组合公式

C（n，2）=n(n-1)/2

（3）、绝对值运算

x³-y³=﹙x-y﹚﹙x²+xy+y²﹚

(x³ + y³) = (x+y)(x² - xy + y²)

2、函数的极限

 函数的极限是函数的一个重要性质，所以必须了解一下。

1、自变量趋于无穷大时函数的极限

定义：设f(x)在{|x|>a>0}上有定义,A是一个常数,如果对于任意给定的ε>0,存在 X(X≥a),使得当 |x|>X时,有|f(x)- A| < ε
要想证明自变量趋于无穷大时函数的极限，只需要证明存在X即可。

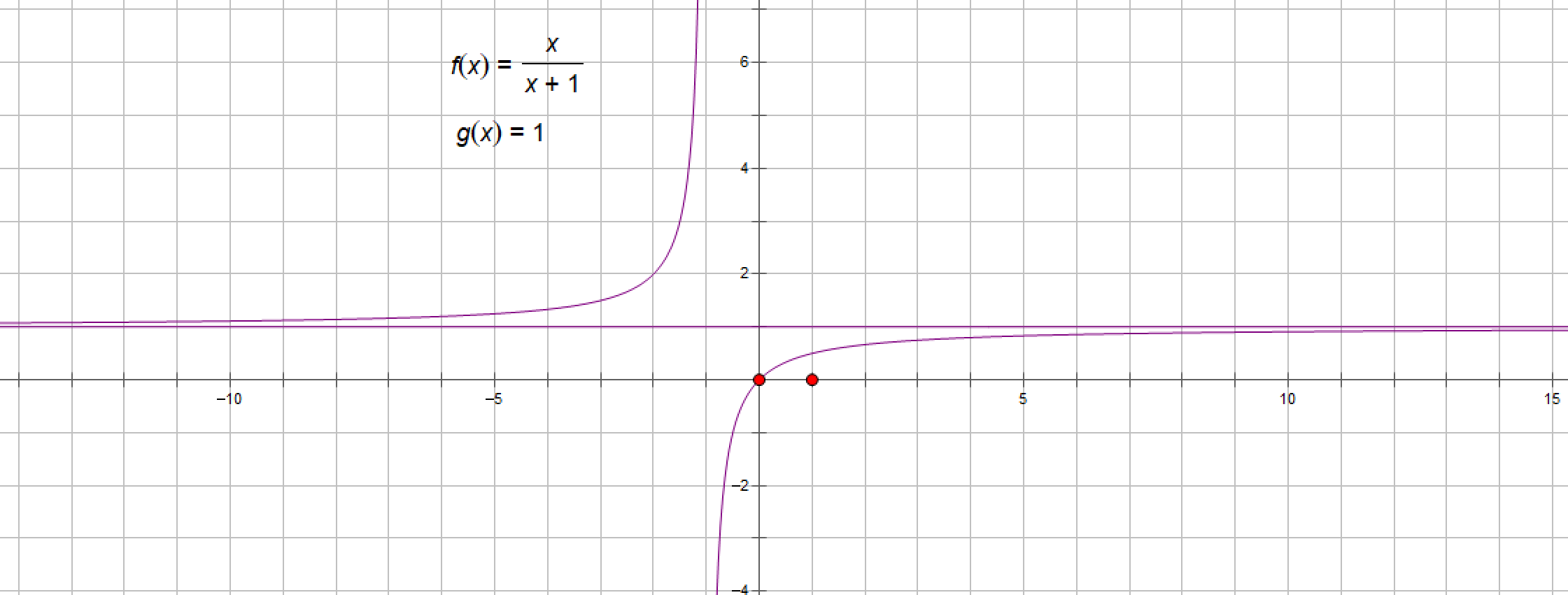
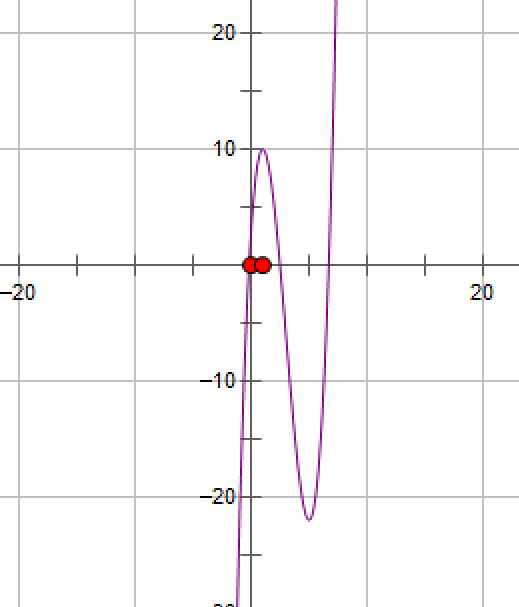
例1：求函数x/(1+x)在x趋于∞时的极限值。

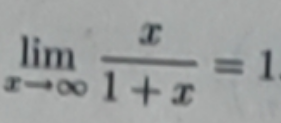
函数x/(1+x)图像如下：

例2：求函数arctanx在x趋于+∞时的极限值

 

 

 

2、自变量趋于有限值时函数的极限

定义：设函数∫(x)在x₀的某个空心邻域U°(x₀,h)中有定义,A是一个常数.如果对于任意给定的ε>0,存在δ>0 使当0<|x-x₀|<δ时,有|f(x)-A| <ε

要想证明自变量趋于有限制时函数的极限，只需要证明存在δ即可。

注 在研究极限时,只考虑函数值在x₀附近的变化趋势,与函数 f(x)在x₀处的值，甚至有无定义没有关系,因此只要求 f(x)在 U°(x_0,h)有定义,不需要考虑f(x)在x₀处是否有定义。

自变量趋于有限值时，求函数的极限值时，不要求函数在x₀处有函数值，也不要求函数在x₀处有定义。

应该注意 定义中的δ只要求存在,不需要找出最大的δ,因此在寻找δ时,可以适当放大|f(x)-A|至 |x-x₀|的常数倍,再确定δ值 (与ε有关)。

例3：求函数（4x²-1）/(2x-1)在x趋于1/2的极限值

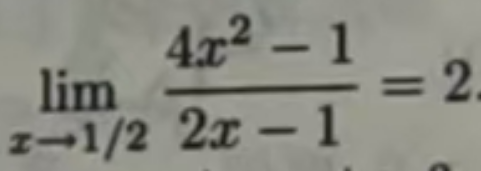
函数在某点上没有定义，可以理解为自变量x不能取该点的X坐标值,换句话说,函数的定义域不包括该点的X坐标值,值域不包括该点的Y坐标值.

函数（4x²-1）/(2x-1)在1/2处没有函数值，但是我们想要知道其极限值。

函数图像如下：

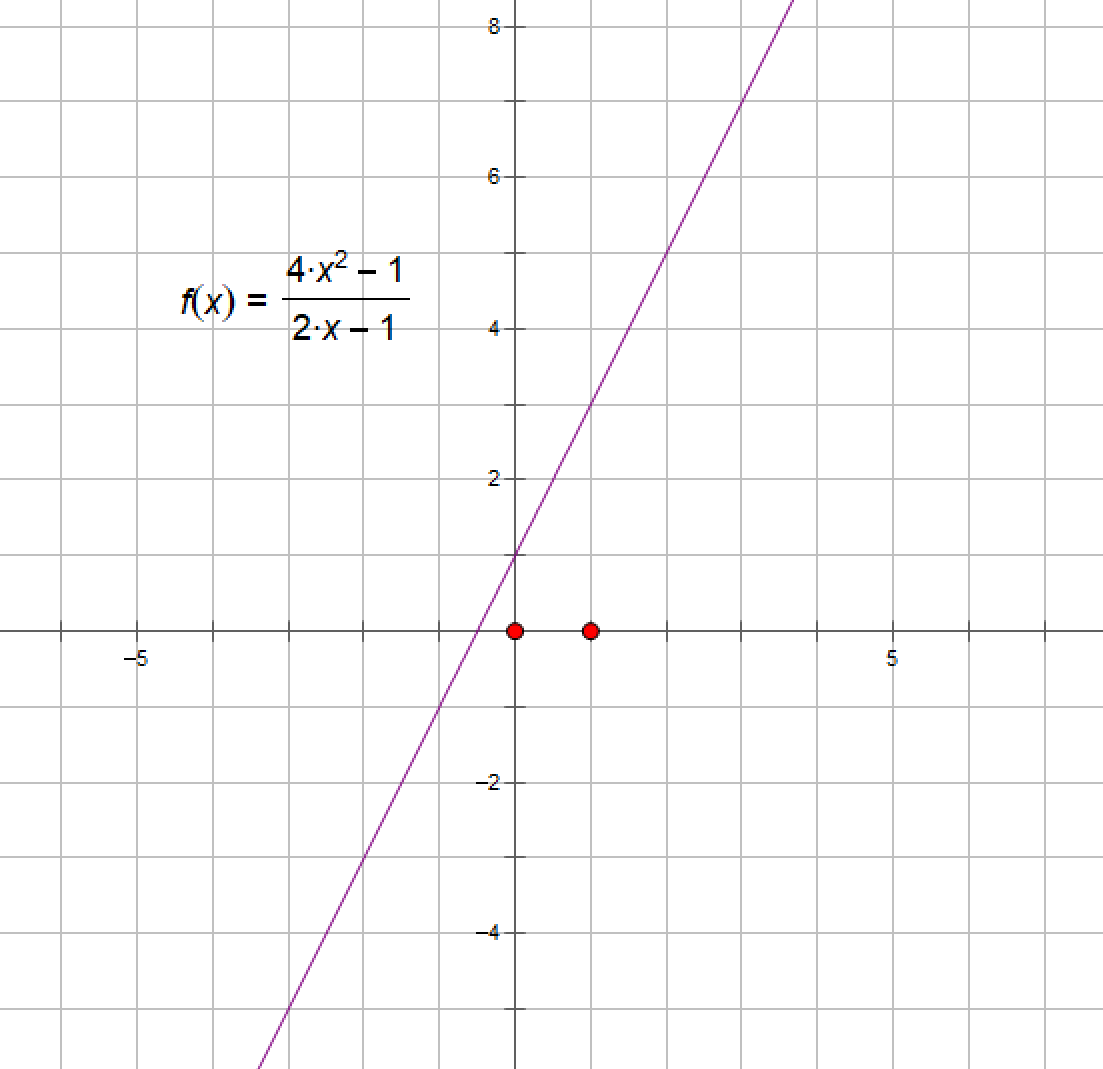
例4:求函数（x³-1）/(x-1)在x趋于1时的极限值

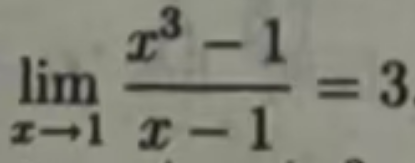
函数的图像：

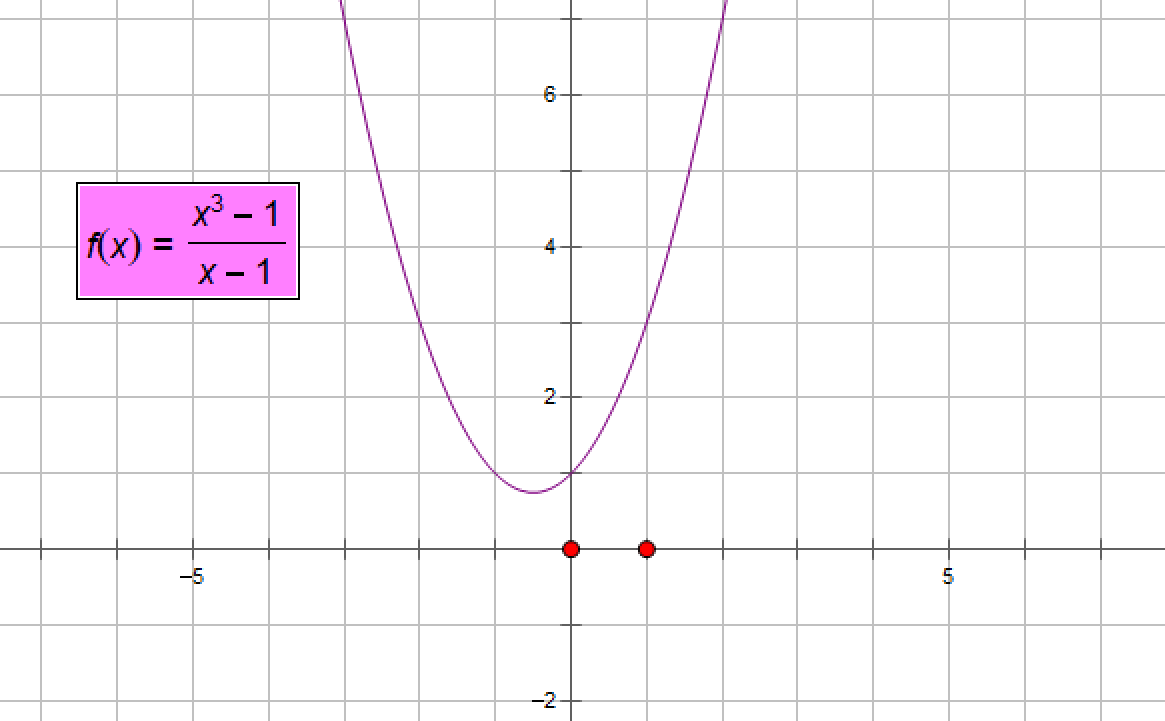
函数在x=1处无定义，也没有函数值，我们求极值只是想知道极限值。

例5：求函数根号x在x趋于x⁰处的极限值

函数图像：

 

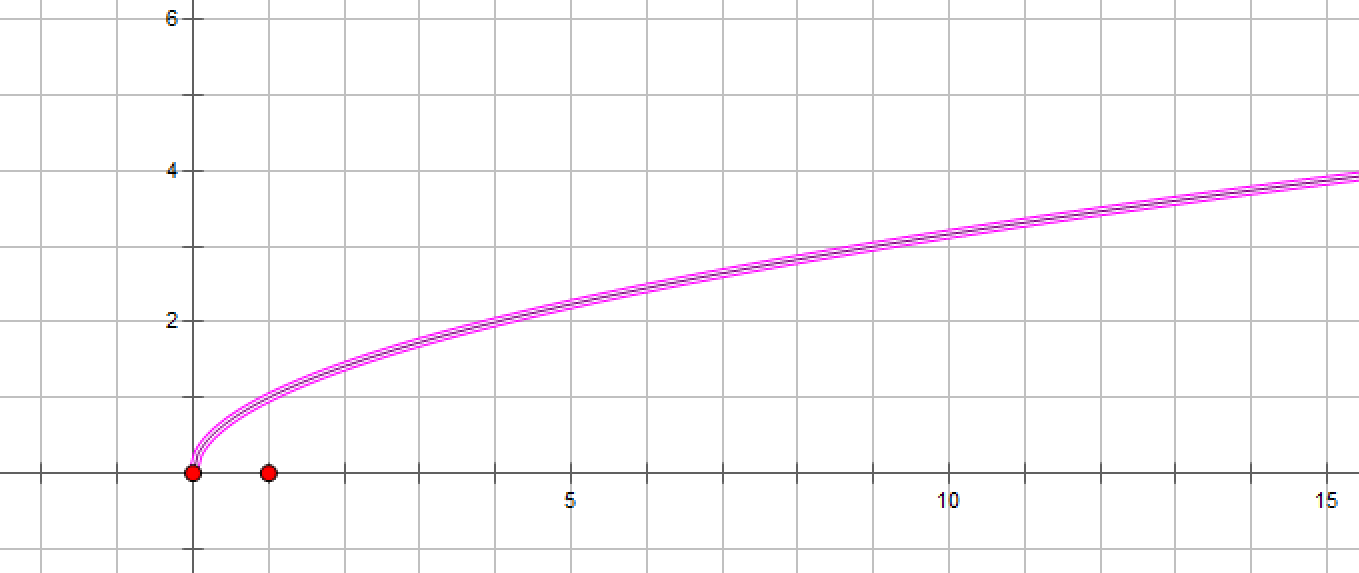
函数极限的性质：

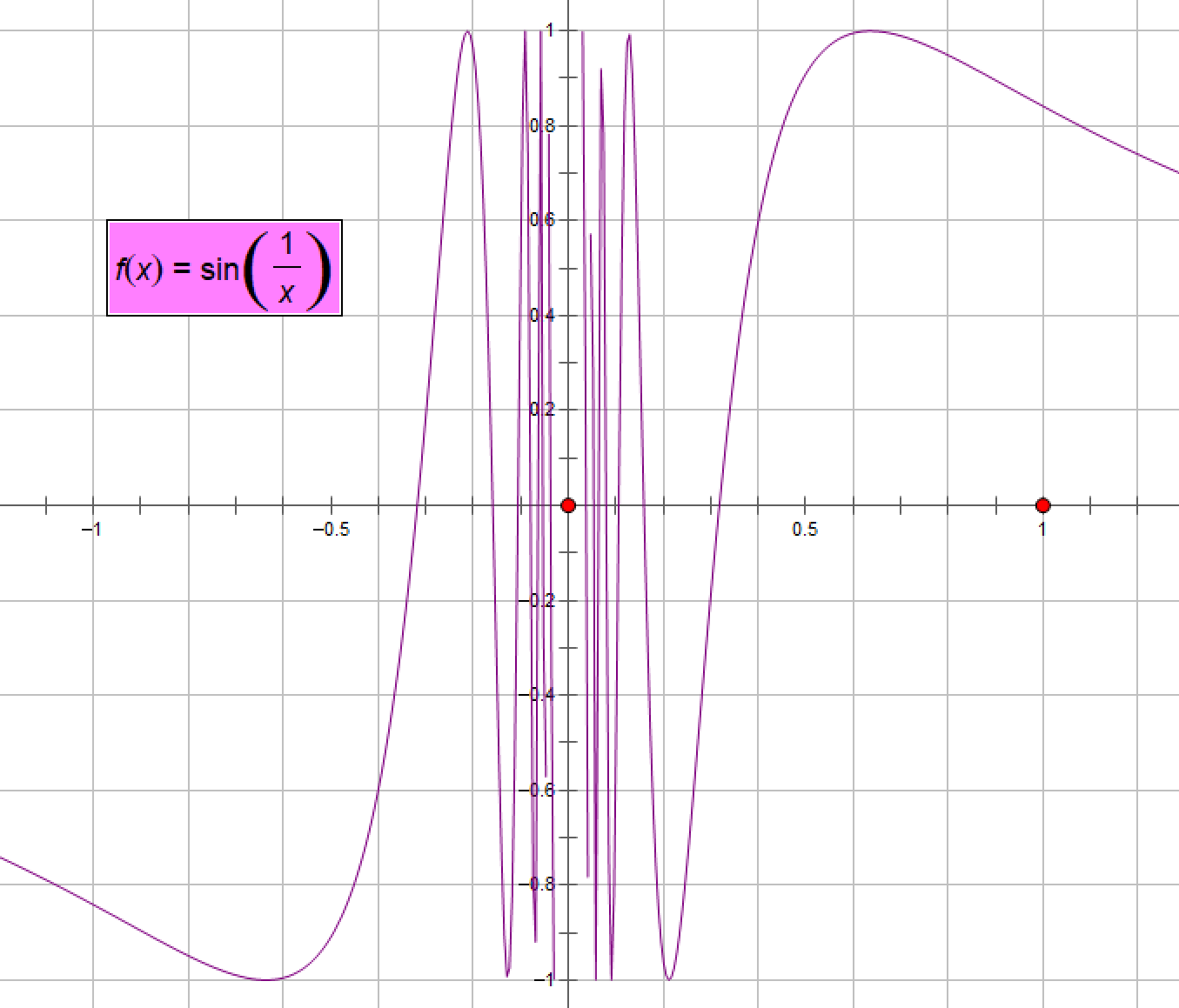
证明sin1/x在x→0时不存在

根据上面的推论，要证明x→0时sin1/x的极限存在，就要证明数列{x_n}在x_n→0时，f(x_n)在n→∞的极限存在。

如果取x_n'''=1/(2nπ-π/2)，此时n→∞时，f(x_n''')的极限为-1，故由于n→∞时f(x_n)的极限在[-1,1]之间不断的变化，故sin1/x在x→0时的极限不存在，同理cos1/x在x→0时的极限y也不存在。

sin1/x的函数图像：

函数极限的运算:

两个重要的极限：

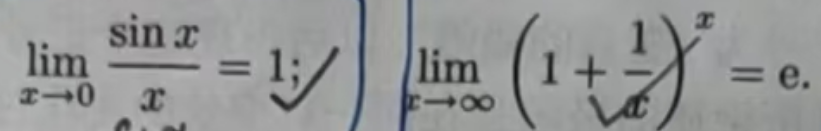
应用：利用这两个重要的极限计算其他函数的极限。

 

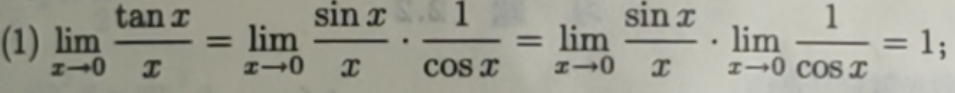
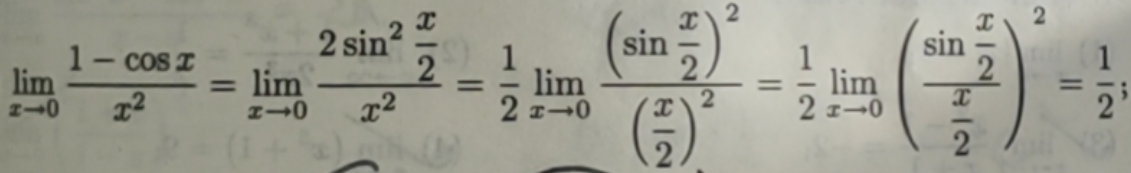
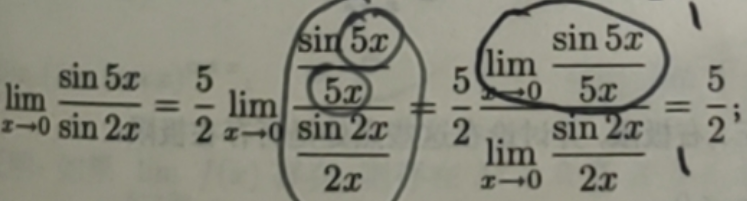
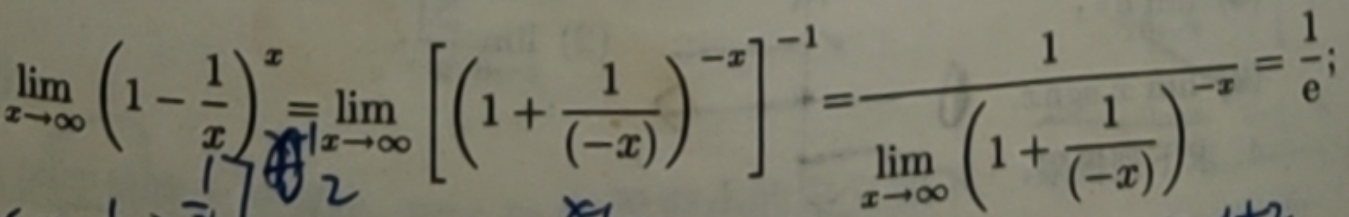
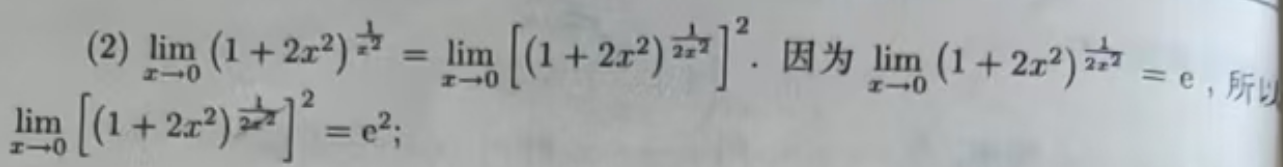
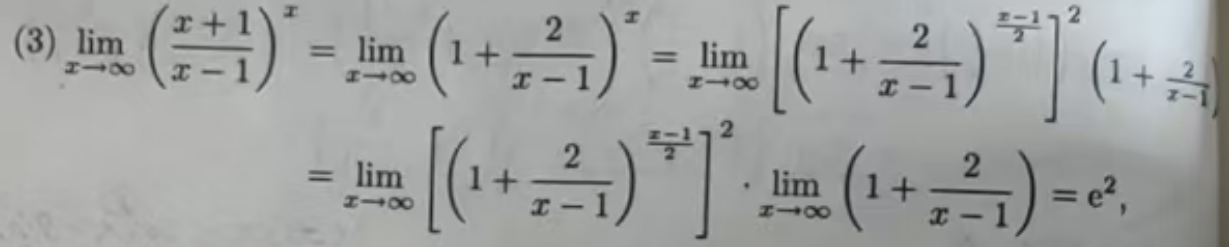
3、利用等价无穷小来求极限

1、无穷小

定义：设函数f(x)在 U°(x₀;h)上有定义,如果对任意给定的ε>0,存在δ>0,当0<|x-x₀|<δ时,有|f(x)|< ε,则称函数f(x)是x→x₀时的无穷小；

注意：（1）、x→x_{0时，函数f(x)是无穷小。（2）、无穷小不是-∞，-∞是沿x轴负向的无穷大。}

注  无穷小是一个变量f(x)的变化过程,不要与很小的常数混为一谈.根据无穷小定义,常数中只有零才是无穷小。当提及无穷小时,一定要指出自变量的变化过程。这与函数极限一定要指出变化过程是一样的,如y=1/√x,当x→ +∞ 时是无穷小,而当x→1时,就不是无穷小了.

运算性质：

(1)、有限个无穷小的代数和仍是无穷小;

1/x³是x→ +∞时的无穷小，e^-x是x→ +∞时的无穷小，无穷小和无穷小的代数和仍是无穷小。

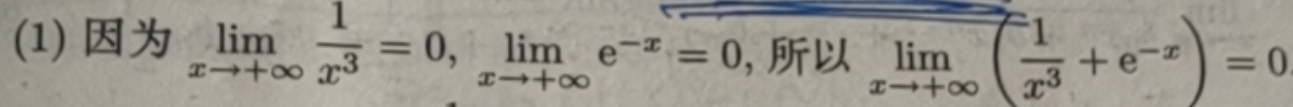
(2)、有限个无穷小的乘积仍是无穷小;

(3)、无穷小与有界变量的乘积仍是无穷小;

x²是x→ 0时的无穷小，sin(1/x)在 U°(0;1)中有界,所以：

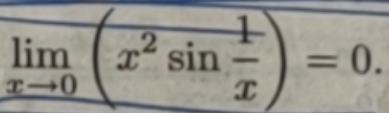
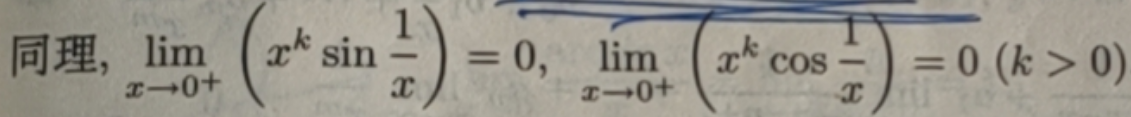
(4)、无穷小与极限不为零的变量的商仍是无穷小,

定理 2.3.2  lim f(x)=A的充分必要条件是存在ェ→x₀时的无穷小 a(x)使得f(x)= A+a(x).

 

2、无穷大

定义  设函数f(x)在U°(x₀;h)中有定义.如果对于任意正数M,存在6>0,使当0<|x-x₀l<δ时,有|f(x)|> M,则称函数 f(x)是x→x₀时的无穷大,记为

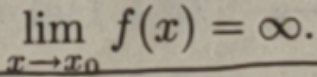
这样只是为了表达方便,并不是说x→x₀时 f(x)的极限存在.

 

定理 2.3.3(无穷大与无穷小的关系)在自变量的同一变化过程中,如果f(x)是无穷大,则1/f(x)是无穷小;反之,如果 f(x)是无穷小,且f(x)≠0,则1/f(x)是无穷大。

例1：求1/（1+x）在x→-1时的极限

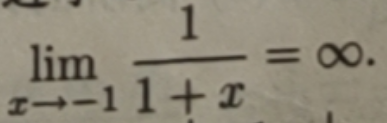
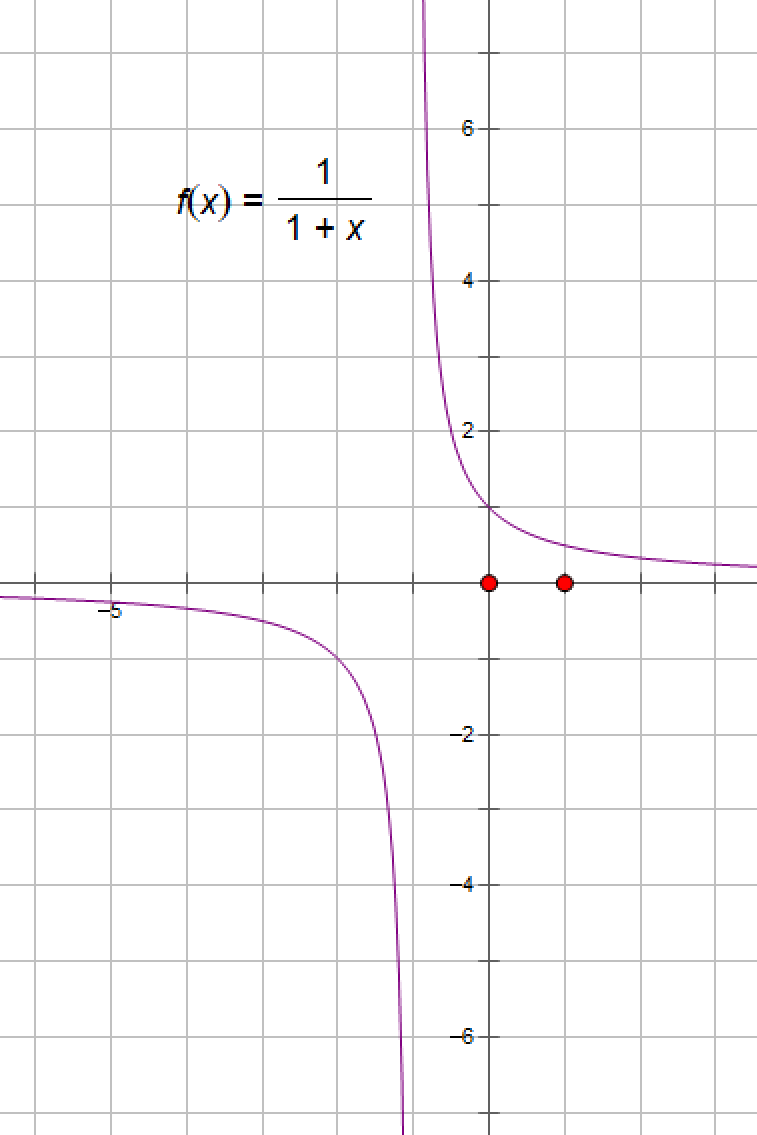
注意无穷大与无界的区别,无穷大一定是无界函数,而无界函数不一定是无穷大。

函数 f(x)= xcos 在(-∞,+∞)内无界, 但当 x → +∞ 时,f() 不是无穷大

 

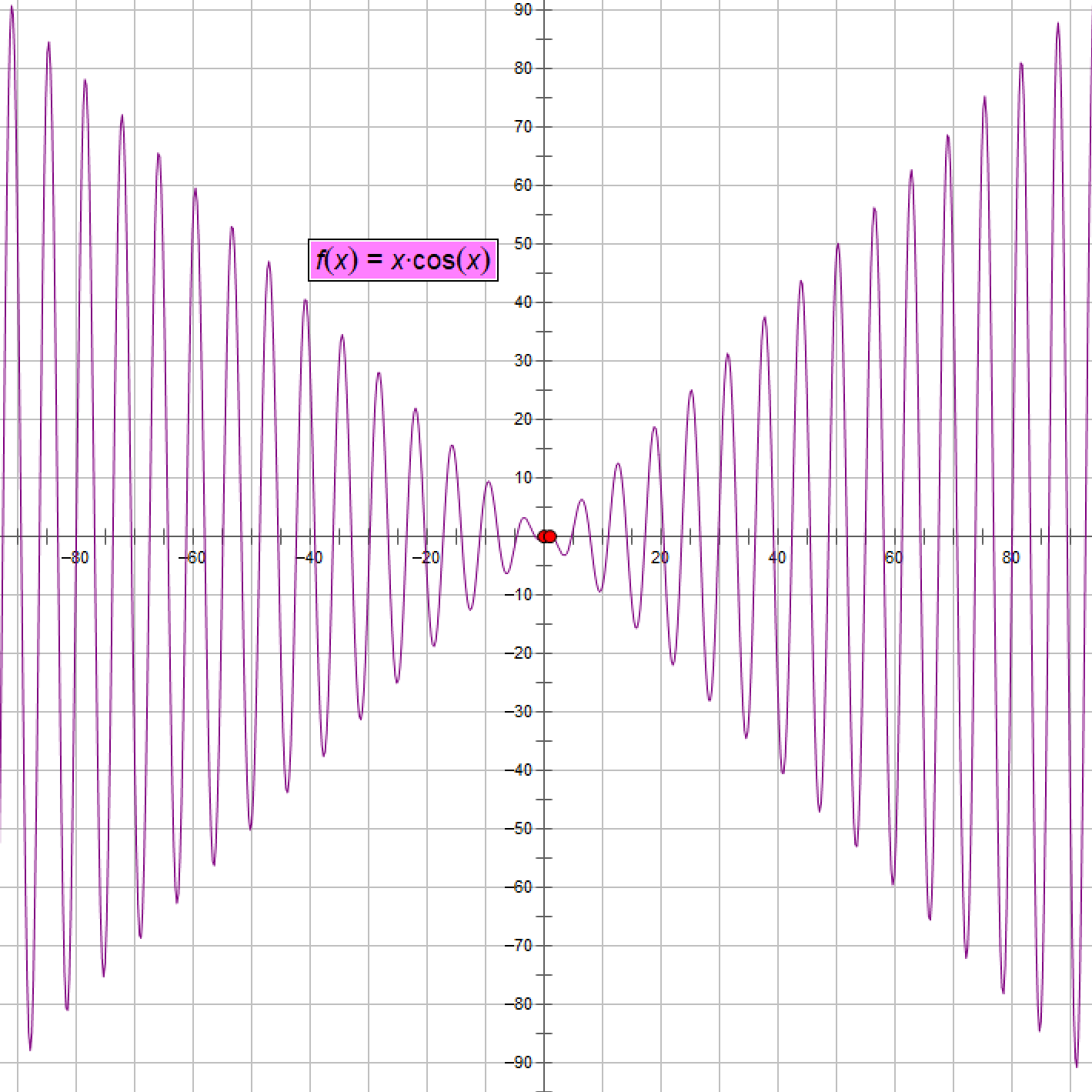
3、无穷小的比较

我们知道,当 x → 0 时x,sin2x，x^1/3,x²都是无穷小,但却有

      

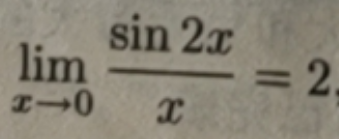
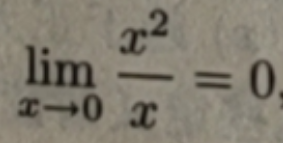
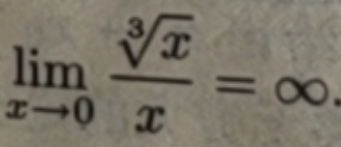
虽然都是无穷小,但是趋于0的速度有快有慢,甚至相差很大,所以对无穷小的量级要建立一个评判法则.

 定义 2.3.3 设 α(x),β(x)是同一自变量变化过程中的无穷小,并且 lim α(x)/β(x)也是这个过程中的极限.

(1)、如果 lim α(x)/β(x)=0,则称 α(x)是比 β(x)高阶的无穷小,记作 α(x)=o( β(x));

(2)、如果 lim α(x)/β(x)=l≠0,则称 α(x)是与 β(x)同阶的无穷小,特别当l=1时，称 α(x)是与 β(x)等价的无穷小,记作 α(x)~ β(x);

(3)、如果lim α(x)/β^k(x)=l≠0(k> 0),则称 a(x)是关于 β(x)的k阶无穷小;

(4) 、如果 lim α(x)/β(x)=∞,则称 a(x)是比β(x)低阶的无穷小;

(5)、a(x)是比β(x)高阶的无穷小等价于,β(x)是比a(x)低阶的无穷小；

于是,当x→0时,x²是比ェ高阶的无穷小,而x是比x^1/3 高阶的无穷小.

x~sin(x) (x→0)，x~tan(x)(x→0)，1-cos(x)~1/2x² (x→0)，x~arcsin(x) (x→0)，x~ln(x+1) (x→0)，x~e^x-1 (x→0)，(1+x)^b-1~ bx (x→0),

前面这些基本的等价无穷小非常有用,请务必记住.

另外,上述等价无穷小中的x也可以换成某个x的函数φ(x),只要在变化过程中 φ(x)→0即可,于是有

√x~ sin √x (x → 0),x²~e^x2 -1(ェ → 0)

定理 2.3.4  设 α,α1,β,β1 都是同一自变量变化过程中的无穷小,且α~α1,β~β1,limα1/ β1 存在,则limα/ β= limα1/ β1.

这个定理的好处是在求商的极限时,分子、分母中的无穷小因子都可以用相对简单的等价无穷小进行替换,以简化求极限的过程,

最后请注意,无穷小的比较并不是任何时候都可以进行的,如x→0时,xsin(1/x)、x都是无穷小,而进行比较则不行,因为xsin(1/x)/x=sin(1/x)，当x→0时极限不存在。

三、函数的连续性

上面我们学过了函数的极限，下面需要根据函数的极限来讲函数的连续性，极限是学习函数的连续性的基础。

1、函数的连续性

定义 2.4.1 设函数f(x)在U(x₀;h)上有定义,如果,则称函数 f(x) 在点x₀ 连续,并称点 x₀ 为f(x) 的连续点.

即在x₀处的极限值等于函数值。

定义 2.4.1' 设函数 f(x)在U(x₀;h)上有定义,Δy=f(x₀+Δx)-f(x₀)，如果，则称函数f(x)在点x₀连续。

这里用增量来描述连续性更能说明(连续”)这一概念的本质:连续就是自变量变化很小时,函数值的变化也很小。

定义 2.4.2设函数f(x)在U(x₀;h)上有定义,如果对于任意给定的ε>0,存在δ>0(δ≤h),使当 |x-x₀|<δ时,有|f(x) - f(x₀)|< ε,则称函数 f(x)在点x₀连续.

定义 2.4.3 设函数在区间[x₀,x₀+h)(或(x₀-h,x₀])上有定义,如果则称函数 f(x)在点x₀右连续(或左连续).

定理 2.4.1 函数f(x)在x₀处连续的充分必要条件是:函数f(x)在x₀处既左连续又右连续.

如果函数 f(x)在某区间的每一点都连续,就称 f(x)在该区间上连续,或称f(x)是该区间上的连续函数,如果该区间包含了端点,则函数连续在左端点是指右连续,在右端点是指左连续.

当函数 f(x)的定义域由一些区间组成,且在这些区间上都连续,就称f(x)在其定义域上连续,或称f(x)是连续函数,

2、间断点及其分类

函数不连续就是函数的图形曲线有间断,仔细分析f(x)在x₀处不连续的原因有三种：

第一,f(x)在x₀处没有定义;(可去间断点)

第二,极限不存在;（跳跃间断点）

第三,极限虽然存在,但不等于 f(x₀).(可去间断点)

上面三条中只要满足其中一条,就称 f(x)在x₀处间断,或称x₀是f(x)的间断点.

根据间断的原因,函数f(x)的间断点可以分成以下几种类型:

(1)如果 f(x₀+0),f(x₀-0)都存在,则称点 x₀是函数f(x)的第一类间断点.

(2)如果 f(x₀+0),f(x₀-0)中至少有一个不存在,则称点 x₀ 是函数 f(x)的第二类间断点.

第一类间断点根据不同的情况,又可以分为可去间断点(存在,但不等于 f(x₀),或 f(x)在x₀处没有定义)和跳跃间断点(f(x₀+0)≠f(x₀-0)).

可去间断点,顾名思义就是通过重新定义f(x)在点 x₀ 的值,即就可使f(x)在x₀处连续的间断点

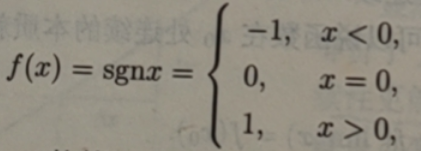第一类间断点（跳跃间断点）

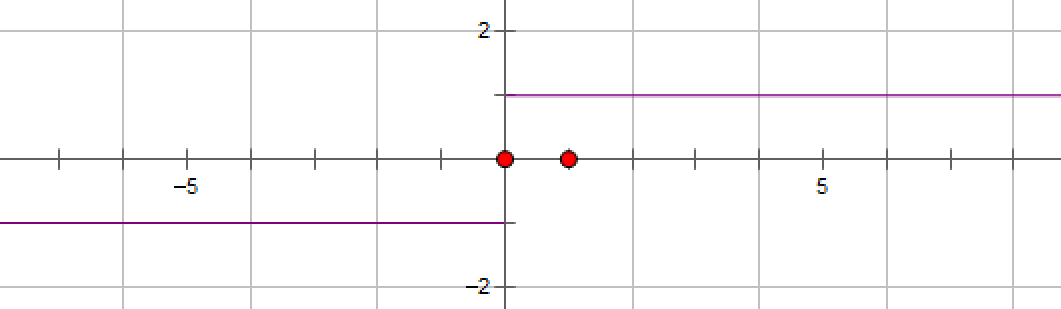
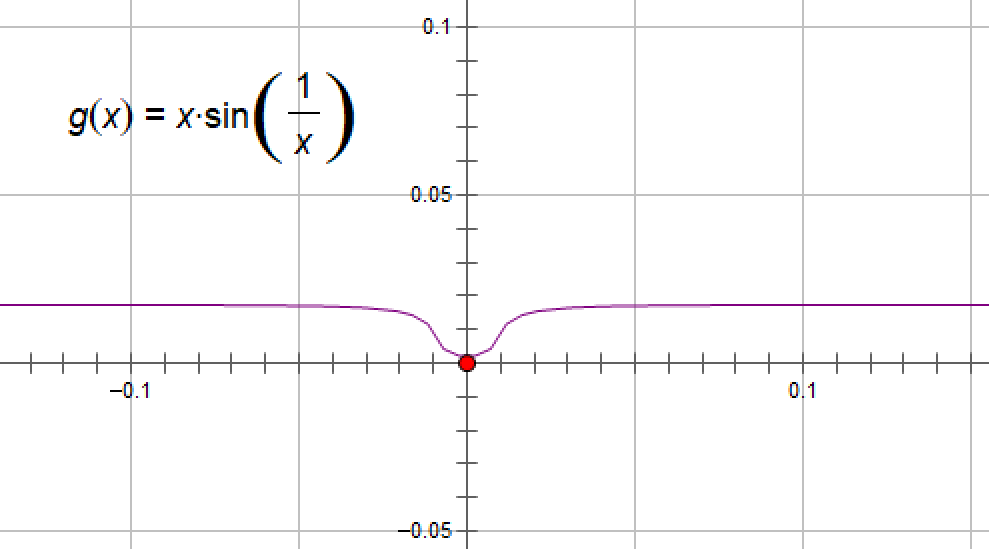
f(x)=xsin(1/x)第一类间断点（可去间断点）

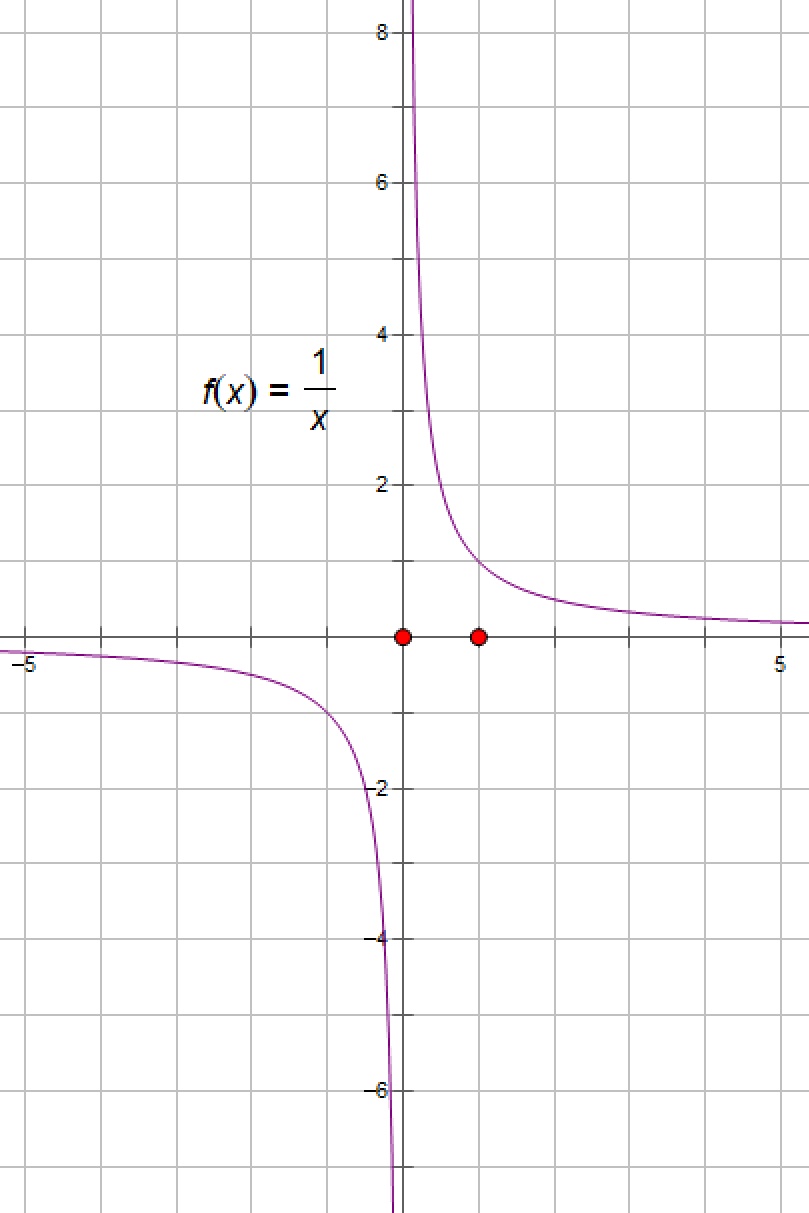
f(x)=1/x第二类间断点（无穷间断点）

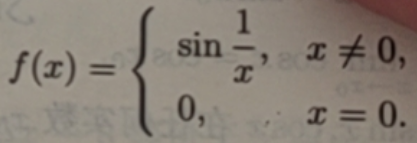第二类间断点（振荡间断点）

 

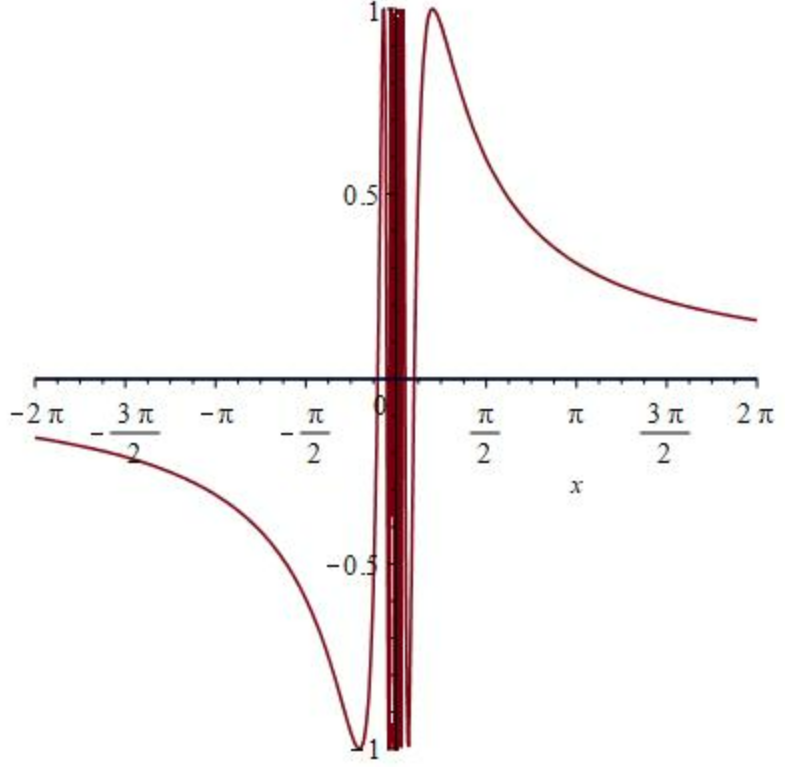
跳跃间断点经常在分段函数中出现，而可去间断点多出现在分式函数或分母中有自变量的函数中。

3、连续函数的运算和初等函数的连续性

定理 2.4.2设函数f(x),g(x)都在点x₀连续, 则 f(x)± g(x),f(x)g(x) 和f(x)/g(x)(g(x)≠0)在x₀也连续.

定理2.4.3设函数y=f(x)是区间I上严格单调增加(或减少)的连续函数,则其反函数y=f^-1(x)是区间J=f(I)上严格单调增加(或减少)的连续函数。

定理 2.4.4 设函数u=g(x)在ェ→x₀ 时有极限u₀,即，函即y=f(u)在u=u₀处连续, 则复合函数 y=f(g(x))在ェ→x₀时的极限为 f(u₀)即

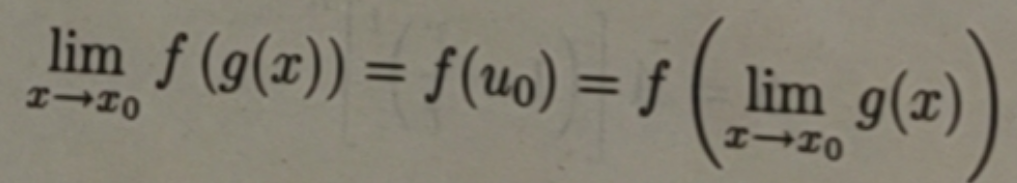
特别当 u= g(x)在x₀ 处连续,μ=f(u)在点u₀=g(x₀)处连续时,复合函数y=f(g(x))在点 x₀ 处连续.

即外层函数连续，内层函数也连续，则复合函数连续。

定理 2.4.4说明如果复合函数中的每一层函数都是连续函数,求极限运算可以与函数运算层层交换.

也就是说复合函数的极限可以先求里面函数的极限值后进行外层函数的运算。

例：x→0时，lim cos (1+ x)^1/x = cos lim (1+ x)^1/x = cose;

由此可知，基本初等函数在各自定义域中连续,根据定理 2.4.2~2.4.4就可以得到初等函数在其定义域内的区间上连续,即初等函数是其定义区间上的连续函数，

因此求初等函数在定义区间内的点的极限就变为求该点的函数值。

4、闭区间上连续函数的性质（最值定理和介值定理）

定理 2.4.5(最大、最小值定理)如果f(x)在闭区间[a,b]上连续,则在闭区间[a,b]上至少存在两个点ξ,η,使当x属于[a,b]时,有f(ξ) ≤ f(x) ≤ f(η),这里 f(ξ)和 f(η)分别称为 f(x)在[a,b]上的最小值和最大值。

注意：只有是闭区间且连续，则会有最大值和最小值。

函数 f(x)在[a,b]上连续是 f(x)在[a,b]上有最大、最小值的充分条件.如函数f(x)在[a,b]上有间断点就不一定有最大、最小值,

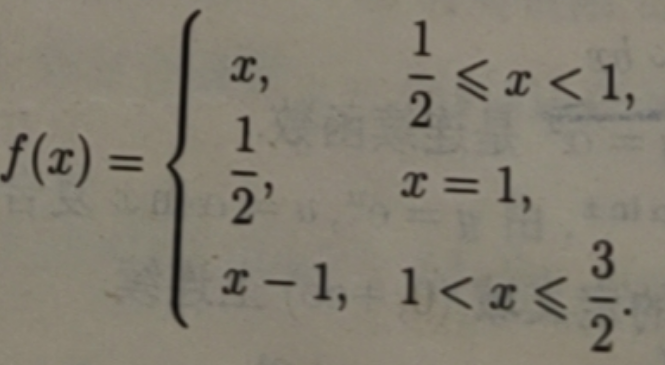
图像如下：

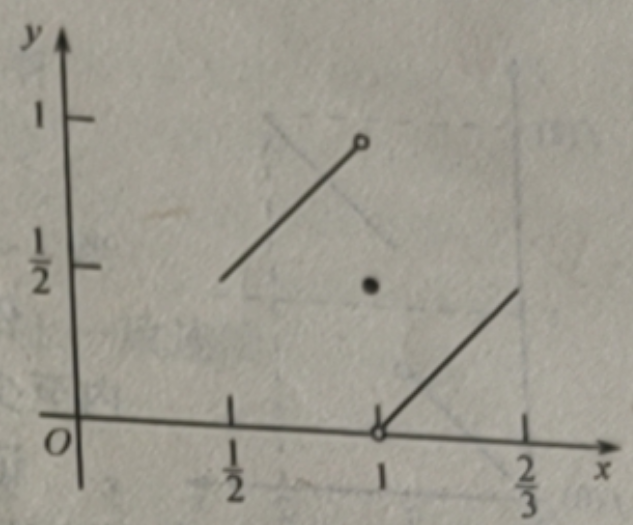
定理 2.4.5 在开区间(a,b)上也不一定成立.如f(x)=1/x在(0,1)上连续,但在(0,1)上既没有最大值,也没有最小值.

推论(有界性定理)如果f(x)在闭区间[a,b]上连续,则 f(x)在闭区间[a,b]上有界.

定理 2.4.6(介值定理)如果函数f(x)在闭区间 [a,b]上连续,且 f(a)≠ f(b),则对介于f(a)与f(b)之间的任何实数c,在开区间(a,b)内至少存在一点ξ,使得f(ξ)= c

推论 1 如果函数 f(x)在闭区间[a,b]上连续,M,m 分别是 f(x)在[a,b]上的最大值和最小值(M>m),则对于任何实数c(m<c<M),在(a,b)内至少存在一点ξ,使得f(ξ)= c

推论2(根的存在定理)如果f(x)在闭区间[a,b]上连续,且 f(a)·f(b)<0,则在开区间(a,b)内至少存在一点ξ,使得f(ξ)= 0.

当 f(x)在|a,b]上有间断点时 定理 2.4.6 及推论中的结论不一定成立.例如:

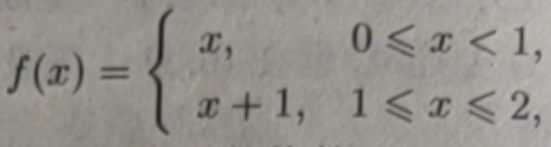
函数图像

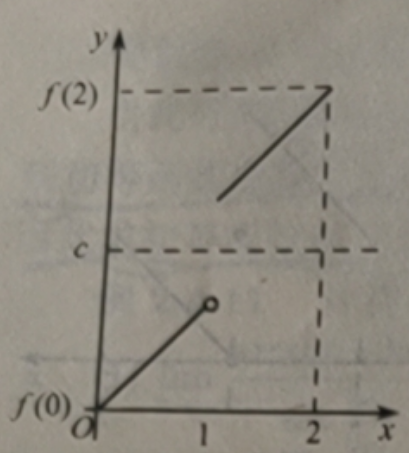
当1<c<2时,就没有函数值等于c

5、函数的一致连续性

经过前面的讨论,我们对连续的概念有了比较全面的了解,但是一旦继续深入思考一些问题,就会产生一些疑问:函数在x₀处连续是指Δy=f(x₀+Δx)-f(x₀)→0(当Δx → 0时).

由于函数在不同的点形状不一样,有的平坦有的陡,当Δx趋于0时,Δy 趋0的速度就会不一样,这种不一样是否会像无穷小那样有不同的阶呢?如果这样,函数在不同点的增量就有本质的差异;如果不是,就没有本质上的差异,这种函数增量趋于0的快慢的思考,就引出了“一致连续”的概念.

定义2.4.4设函数f(x)在区间I上有定义,如果任给ε>0,存在δ>0.对I上任意两点 x1,x2 属于I, 只要|x1-x2|<δ,就有|f(x1)- f(x2)|< ε,则称函数f(x)在区间I上是一致连续的.

“一致连续”的实质就是在I上任何一点x₀的函数增量Δy随Δx趋于0的度没有本质的差别,是“同阶”的.由此,不一致连续就是Δy当Δx趋于0时趋的速度,在各点之间有本质差别,不是“同阶”的.

定理 2.4.7 闭区间[a,b]上的任一连续函数都是[a,b]上的一致连续函数。

也就是说在有界闭区间上，连续函数一定是一致连续的。

f()=1/x在闭区间 [a,1](0<a<1)上一致连续,但是f()=1/x在开区间(0,1]上不一致连续,这是由于当x越来越靠近0时,函数的图形越来越陡,函数增量趋于0的速度有本质的差别,因此失去了“一致”性.

‌学习函数的一致连续性在数学分析中有以下几个主要用途‌：

1、理解函数的整体性质‌：一致连续性是函数整体性质的一个重要概念。它不仅要求函数在每个点都连续，还要求函数在整个定义区间上的变化不能太快。这种整体性质在数学分析中非常重要，有助于理解函数的整体行为‌。

2、‌证明连续函数的可积性‌：一致连续性在证明连续函数的可积性方面有重要作用。例如，在黎曼积分中，一致连续性是函数可积的一个充分条件。这意味着如果一个函数在某个区间上一致连续，那么它在这个区间上就是可积的‌。

3、与其他数学概念的联系‌：一致连续性与函数的有界性、可积性等概念紧密相关。例如，在有界闭区间上，连续函数一定是一致连续的，反之亦然。这种联系有助于更好地理解函数的性质‌。

4、应用实例‌：一致连续性在实际应用中也有重要作用。例如，在设计零件时，需要确保函数的整体变化不会太快，以避免在实际应用中出现大的误差。此外，一致连续性还可以用于证明某些数学定理，如Arzela-Ascoli定理，该定理在函数序列的收敛性分析中非常重要‌。

5、与其他数学概念的区别‌：一致连续性与局部性质的连续性不同。连续性是逐点定义的，而一致连续性要求在整个定义区间上函数的变化不能太快。这种区别有助于更好地理解函数的局部和整体性质‌。

四、导数（切线和法线）

1、导数的概念

 导数是微积分学中最基本的内容,是微分学的核心概念,是人们研究函数增量与自变量增量关系的产物,又是深刻研究函数性态的有力工具.无论何种学科,只要涉及“变化率”,就离不开导数,因此导数在物理学、力学和经济学中都有广泛的应用.

一般认为,求变速运动的瞬时速度,求已知曲线上一点处的切线,求函数的最大、最小值,以及求曲线的弧长是微分学产生的4个动因.

牛顿和莱布尼茨分别在研究瞬时速度和曲线的切线时发现了导数.

这些问题的实质就是研究自变量x的增量 Δx 与相应的函数 y= f(x)的增量 Δy 之间的关系,即研究当 Δx →0时,Δy/Δx 的极限是什么.下面是两个关于导数的经典例子.

1.变速直线运动的瞬时速度(距离的变化率)

设质点沿直线运动,其位移s是时间t的函数,即s=s(t).当t在t0处有一个增量Δt≠0时,相应地,位移s也有一个增量,即As=s(t0+Δt)-s(t0),

因而质点从时刻t0到时刻 t0+Δt这段时间内的平均速度为

当Δt→0时,若平均速度的极限存在,则其极限

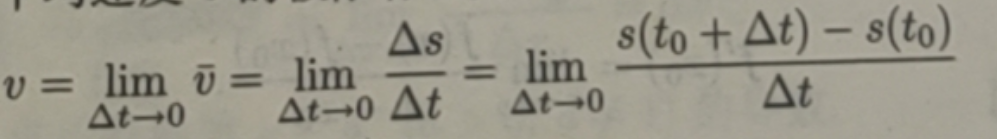
称为质点在时刻t0的瞬时速度

2.曲线在一点处切线的斜率

设曲线C是某函数y=f(x)的图形.如图 3.1所示,A(x₀,f(x₀))是曲线C上的一个定点,B(x₀+ Δx,f(x₀ + Δx)是曲线 C 上邻近于 A 的点(Δx≠0),则割线AB 的斜率为

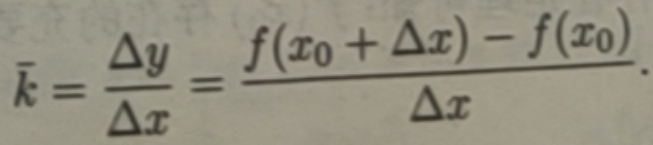
当点B沿曲线C移动并趋于点A时,若割线AB有极限位置AT,则称直线AT 为曲线C在点A处的切线、若当x₀→0时,割线AB的斜率的极限存在，则其极限

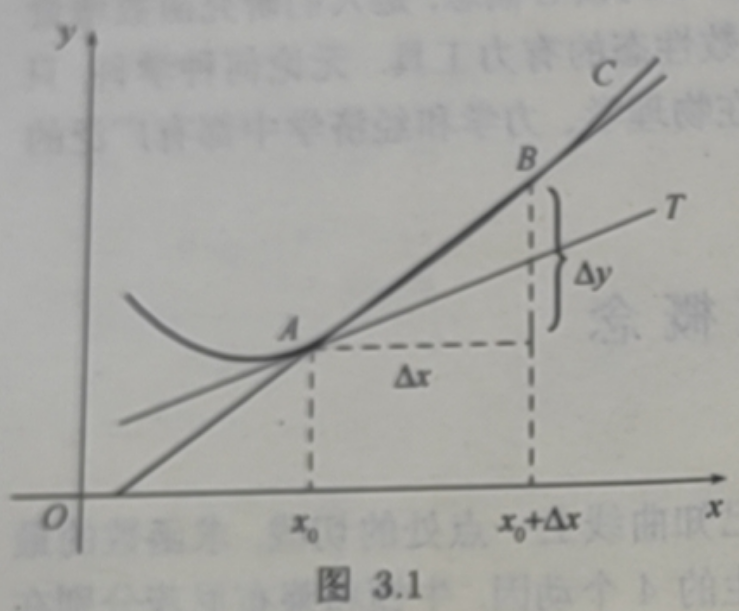
上面两个问题虽然出发点相异，但都可归结为同一类型的数学问题:求函数在点x₀处的增量y=f(x)-f(x₀)与自变量增量Δx=x-x₀之比的极限.这个增量比称为函数f关于自变量的平均变化率,增量比的极限(如果存在)称为f在点x₀ 处关于x的瞬时变化率.因此研究函数的增量Δy与自变量的增量的比值Δy/Δx当Δx→0时的极限具有重要的实际意义.在数学中

极限还称为函数 y=f(x)的导数(或微商).

在点x₀处可导和不可导的定义

定义 3.1.1 设函数y=f(x在点x₀ 的某一邻域内有意义,若极限

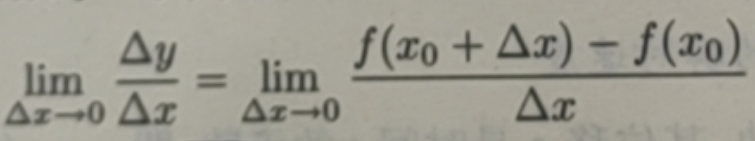
存在,则称函数f(x)在点x₀ 处可导,,并称该极限为函数f(x)在点x₀ 处的导数,记作f'(x),也可以记作 y'(x₀), y'|_x=x0,

若(3.1.1)式的极限不存在,则称f(x)在x₀ 处不可导.

若(3.1.1)式的极限为无穷大,且f(x)在x₀处连续,则可称f(x)在 x₀ 处的导数为无穷大.

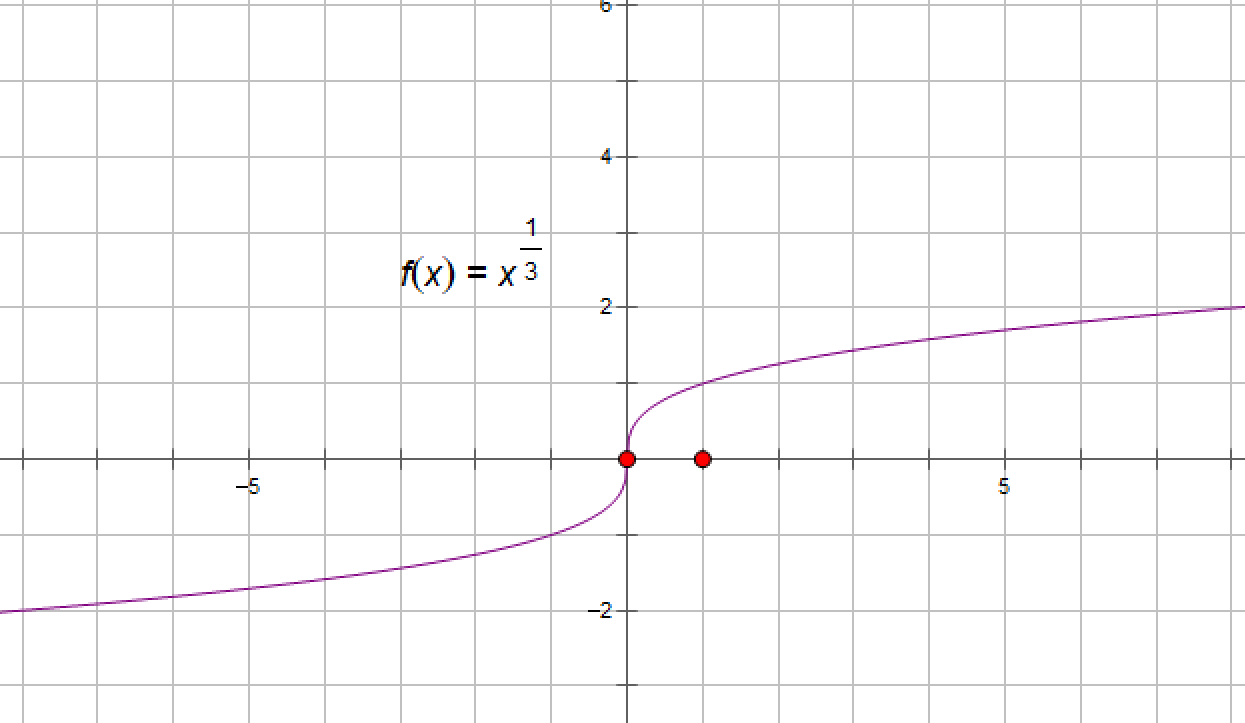
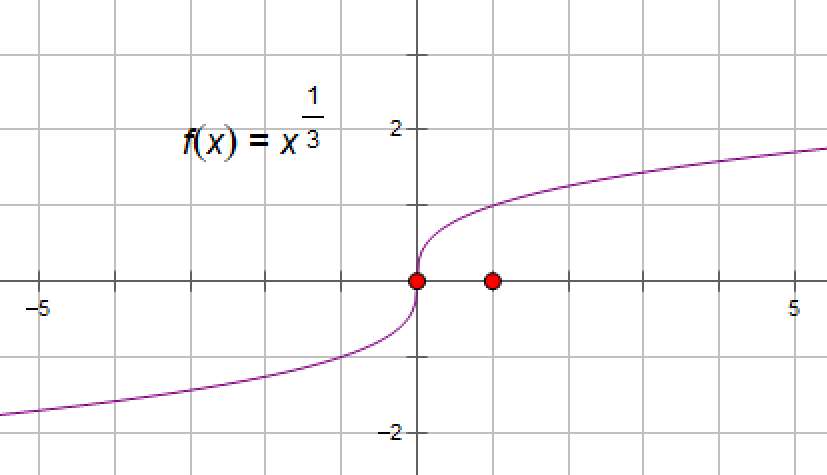
y=x^1/3的图像为：

 f(x)在x₀ 处导数的等价定义为:

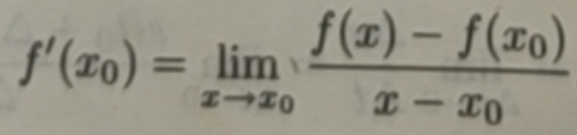
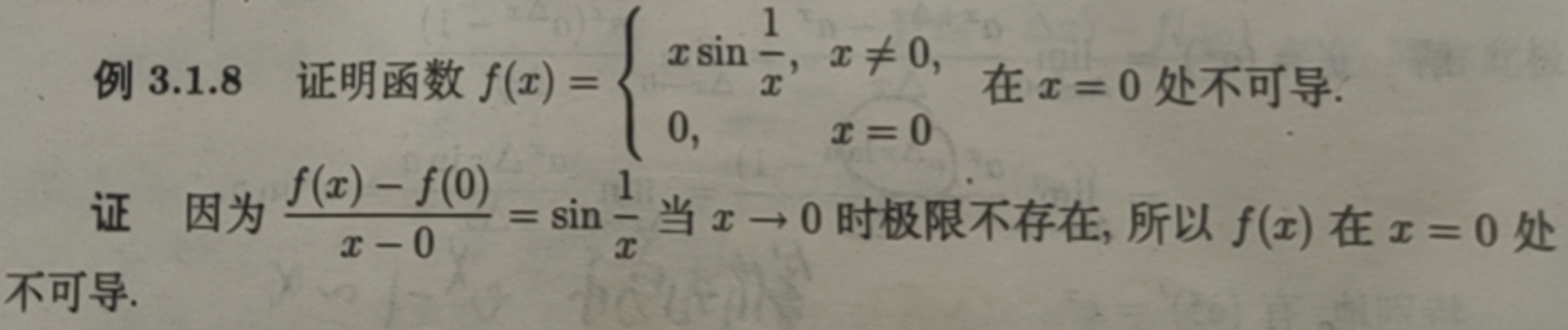
单侧导数（右导数与左导数）的定义：

右导数与左导数统称为单侧导数

根据导数定义及极限存在定理可知:f'(x₀)存在的充要条件是f'₊(x₀)与f'_-(x₀)都存在且相等.即函数在x₀处可导的充要条件是左导数和右导数存在且相等。

导函数

若函数f(x)在区间I上的每一处都可导(对于端点,只要存在相应的单侧导数),则称f(x)在I上可导,其导数值是一个随x而变化的函数,称为导函数,记为f'(x),或y',dy/dx,df/dx

由导数的定义,函数f(x)在点x₀的导数是导函数f'(x)在x₀处的函数值.导函数的定义域由f(x)的可导点全体组成,它一般是 f(x)定义域的一个子集.

另外,根据导数的定义.函数y=f(x)在某一点x可导,说明函数在该点的自変量増量 Δx 与函数的增量 Δy是当 Δx →0时的同阶或高阶无穷小，即有

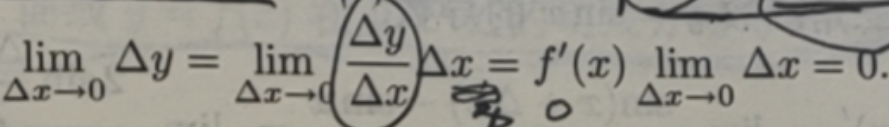
根据定义 2.4.1' 设函数 f(x)在U(x₀;h)上有定义,Δy=f(x₀+Δx)-f(x₀)，如果，则称函数f(x)在点x₀连续。

这表明函数f(x)在x处可导必定连续,简称可导必连续,而函数f(x)在x处连续一般不能得出f(x)在x处可导,请读者务必记住这个性质,

函数y=|x|在x=0处的左、右导数存在,但不可导。

这个性质还说明,连续是可导的必要余件:如果函数在某点不连续,则在该点一定不可导.

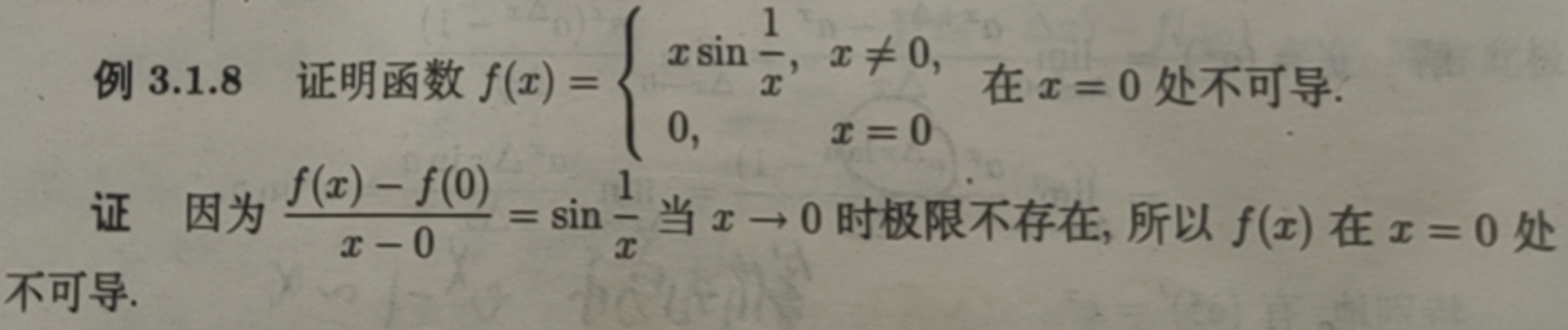
函数图像如下：

该例还说明连续不是可导的充分条件(只是必要条件).

有限增量公式：

由函数y=f(x)在某点 x处可导,还可以得到Δy/Δx-f'(x)=α,其中 α为Δx→0时的无穷小量,因此有Δy = f'(x)Δx +α·Δx,

公式(3.1.2)称为函数f(x)在点x处的有限增量公式.

有限增量公式描述了函数在某一点的变化量与该点的导数之间的关系。设函数f(x)在点x0可导，则函数在x0处的增量Δy可以表示为f'(x0)Δx加上一个高阶无穷小量o(Δx)，即Δy=f'(x0)Δx+o(Δx)。这表明，函数在某一点的变化量主要由该点的导数决定，但还包含一些更高阶的无穷小变化。‌

常量函数y=C的导数为0，幂函数y=x^α(α≠0)，x∈(0,+∞)的导数为αx^α-1,指数函数y=a^x(a>0,a≠1)的导数a^xlna,特别地,有(e^x)'=e^x ,对数函数y=log_ax(a>0,a≠1)的导数为1/（xlna）,三角函数y=sinr的导数为cosx，(cosx)'=-sinx.

对于函数 f(x)在点x₀处导数的定义,可进一步理解其结构式为

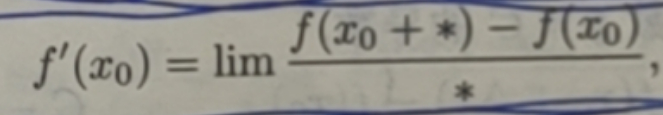
其中*为此极限过程(无论哪个极限过程)中的无穷小,只要符合此结构式,其极限就是 f‘(x₀).

 导数的意义、平面曲线的切线和法线

 从引入导数概念的几何问题可知，函数f(x)在点x₀的导数f'(x₀)是曲线y=f(x)在点 P(x₀,f(x₀))处切线的斜率.如果用α表示这条切线关于x轴的倾角,则有f'(x₀)=tanα.这时,曲线y=f(x)在点P处的切线方程为y-f(x₀)=f'(x₀)(x- x₀),法线方程为x- x₀=-f'( x₀)(y-f( x₀))。

若f(x)在点 x₀的导数为无穷大,且在点 x₀处连续,则曲线在点P处的切线垂直于x轴,这时,曲线y=f(x)在点P处的切线方程为x-x₀=0,法线方程为y-f( x₀)=0

2、求导法则

 导数的四则运算

有了导数的定义,就可以进行求导运算了,但是大家看到,即便是基本初等函数，求导也不是一件容易的事,所以必须建立一些求导法则,使求导变得更为简便.下面就是有关函数加减乘除的求导运算法则：

定理 3.2.1 设函数 u(x)和 v(x)都可导,则

（1）、u(x)±v(x)可导,且 [u(x)±v(x)]'= u'(x)±v'(x)

（2）、u(x)v(x) 可导,且 [u(x)v(x)]'=u'(x)v(x)+u(x)v'(x); 特别,对于常数k,有[ku(x)]’= ku'(x).

 

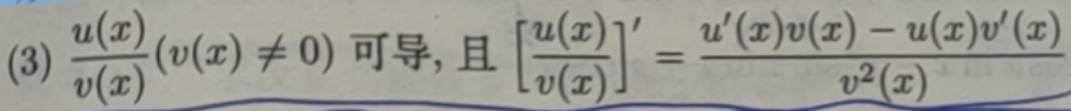
由(1)还可以推出:有限个可导函数代数和的导数等于它们导数的代数和,即

从(2)还可以推出:有限个可导函数的乘积的导数等于每一个函数的导数与其余各个函数的乘积之和,即

[uv···w]'= u'v···w+uv'···w+···+uv...w'

(cot x)' = -1/sin²x = -csc²x

(tan x)' = 1/cos²x = sec² x

(sec x)'  = (1/cosx)' = sinx/cos²x

(csc x)'  = (1/sinx)' = cosx / sin²x

反函数的求导法则

设严格单调的连续函数x=g(y)在点y处可导,且g'(y)≠0.在此情况下，它的反函数y=f(x)存在,且也是严格单调的连续函数.由于Δx≠0与Δy≠0等价,而当Δx →0时Δy→0,反之也对,由此可得反函数y=f(x)的导数与直接函数x=g(y) 的导数的关系

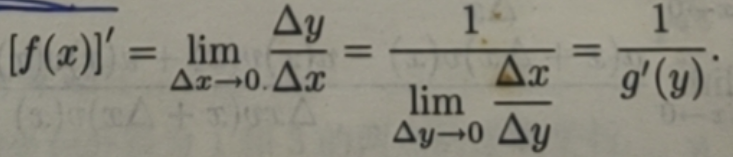
定理 3.2.2 设函数 x= g(y)严格单调可导,且 g'(y)≠0,则反函数 y= f(x)可导,且

注意：求反函数的导数时，说的是反函数y=f(x)与x=g(y)的关系，而不是y=f(x)与y=g(x)的关系。

反正弦函数y=arcsinx的导数(arcsinx)'= 1/√1-x²(-1<x<1)

y= arcsinx(-1<x<1)是x=siny(-1<y<1)的反函数,故(arcsinx)'=1/(siny)'=1/cosy

因为 -π/2<y<π/2,所以 cosy>0,从而 cosy= √1-sin²y= √1-x²,于是(arcsinx)'= 1/√1-x²(-1<x<1)

反余弦函数y=arccosx的导数(arccosx)'==-1/√1-x²(-1<x<1)

y=arccosx(-1<x<1)是x=cosy(0<y<π)的反函数，故(arccosx)'=1/(cosy)'=-1/siny,因为 0<y<π,所以siny>0,siny=√1-cos²y,于是(arccosx)'==-1/√1-x²(-1<x<1)。

反正切函数y= arctanx的导数(arctanx)'=1/(1+x²)(-∞<x<+∞)

y=arctanx(-∞<x<+∞)是x=tany的反函数，故(arctanx)'=1/(tany)'=cos²y=(1/√(1+tan²y))²=1/(1+x²)(-∞<x<+∞)

反余切函数y= arctanx的导数(arccotx)'=-1/(1+x²)(-∞<x< +∞)

y=arccotx(-∞<x< +∞)是x=coty的反函数，故(arccotx)'=1/(coty)'=-sin²y=-(1/√(1+cot²y))²=-1/(1+x²)(-∞<x< +∞)

对数函数y=log_ax的导数(log_ax)'=1/(xlna)(a>0,a≠1,x>0)

y=log_ax(0<x< +∞)是x=a^y的反函数，故(log_ax)'=1/(a^y)'=1/(a^ylna)=1/(xlna)

3、复合函数的求导法则

定理 3.2.3设函数y=f(u)与u=g(x)均可导,且f(g(x))有意义,则复合函数y=f(g(x))在其定义区间内可导,其导数为

 或 

复合函数求导法则又称为链法则.

反复应用此公式可把上述复合函数的求导法则推广到由三个或更多个函数复合面成的函数.例如,若z=f(y),y=g(x),x=h(t)都可导,则[f(g(h(t)))]’= f'(y)g'(x)h'(t)或

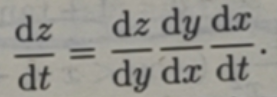
应用复合函数求导法则,实际上是先在被求导的函数中找一个中间变量，以这个中间变量作为自变量的函数可以利用求导公式,再应用复合函数求导法则就可以求得所给函数的导数.例如,求y=e^sinx的导数,令sinx=u,y=e^u,而y对u求导可利用求导公式,u对x求导也可利用求导公式,于是利用复合函数求导法则得

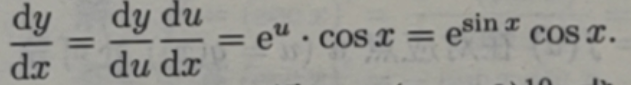
注要进行复合函数的求导,首先将其分解成若干个简单函数,然后再用链法则求导,因此分解特别重要.当熟练掌握链法则后,就不必一一写出中间变量,只要分析清楚函数的复合关系,就可直接求出复合函数对自变量的导数.

 有些函数比较特别,无法分解成能用基本求导公式的函数,如y=x^x,这种函数称为幂指函数,这类函数可以用对数求导法求导.

对数求导法

函数 |f(x)|的对数 In|f(x)[可以看成由w=ln|y|,y=f(x)复合而成,所以

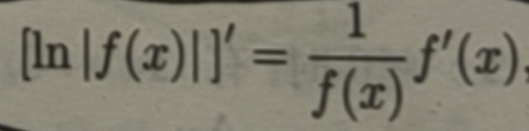则有f'(x) = f(x)[ln |f(x)|]'

称为对数求导法公式,它将求一个函数的导数的问题转化为求这个函数的绝对值的对数导数的问题。幂指函数x^x通过取对数就变成了xlnx,求导十分容易.对数求导法不仅能对幂指函数求导,还能对一些复杂的问题求导

(x^x)' = x^x*(xInx)')=x^x(x·1/x+Inx)=x^x(1+lnx)

(x^sinx)'=x^sinx(sinxlnx)'=x^sinx(cosxInx + sinx/x)

对数求导法还适用于由若千因式连乘、连除所得的复合函数的求导

取对数可以简化函数,变乘幂为乘积,化积、商为加、减,大家可以根据这一特点决定是否用对数求导法。

4、基本初等函数的导数公式与求导法则

由于初等函数是由基本初等函数经过有限次四则运算和复合运算生成的,因此知道了基本初等函数的导数公式及四则运算、复合函数求导法则,初等函数的求导问题就解决了.

基本初等函数的导数公式

(1)(C)'=0(C 是常数);

(2)(x^α)'= αx^α-1(a 为任何实数);

(3)(sinx)'= cosx,     (cosx)'= -sinx,      (tanx)'= sec²x = 1/cos²x,     (cotx)'=-csc²x=-1/sin²x     (secx)'= secxtanx,     (cscx)'=-cscxcotx

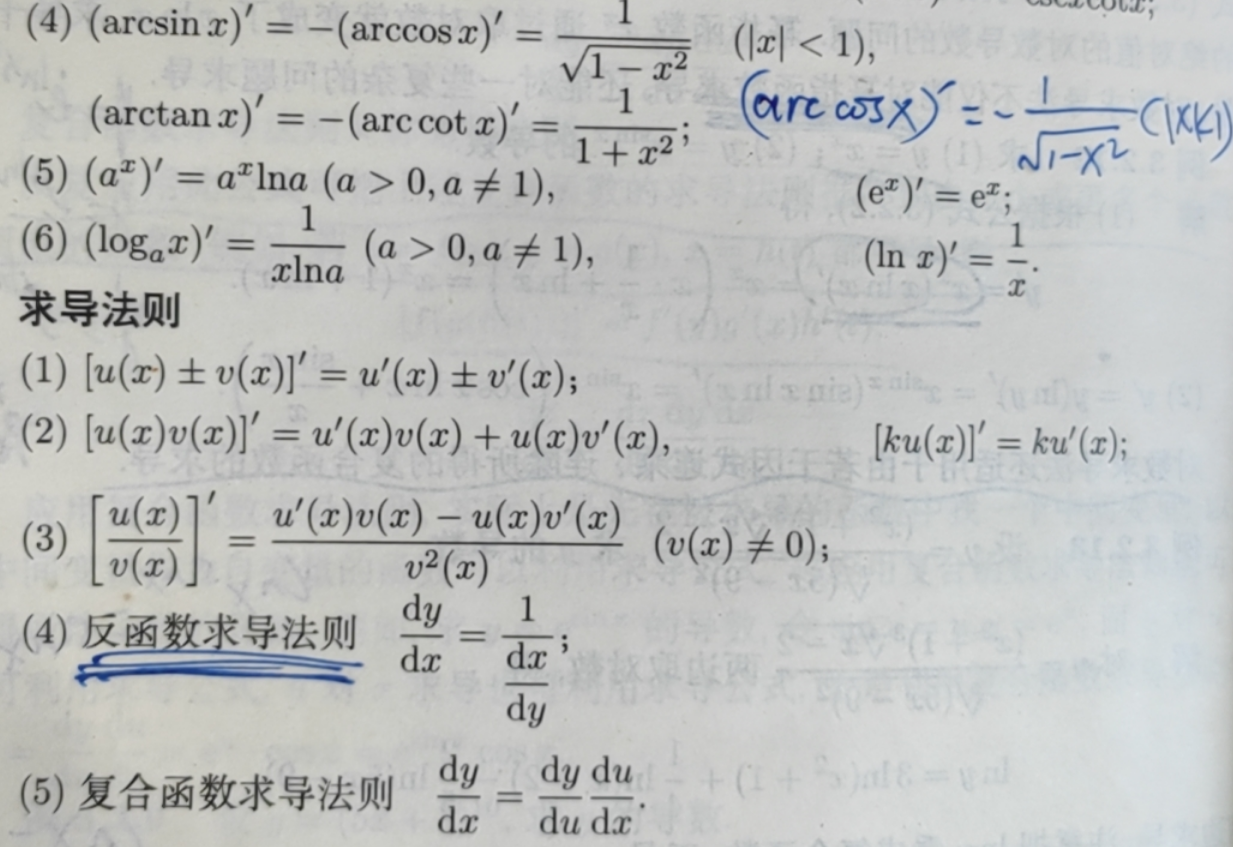
3、高阶导数(二阶及二阶以上的导数)

 学习n阶导数，后面在泰勒公式中会用到n阶导数。

在运动学中,不但需要了解物体的速度,而且需要了解运动速度的变化率,即加速度问题.因为变速直线运动的速度 v(t)是位置函数s(t)对时间t的导数,而加速度a(t)是速度v(t)对时间t的导数,所以加速度a(t)是位置函数对时间t的导数的导数.在工程学中,常常需要了解曲线的斜率的变化程度以求得曲率的弯曲程度,即需要讨论斜率函数的导数问题.在进一步讨论函数的性质时,也会遇到类似的情况,也就是说,对一个可导函数求导之后,还需要研究其导函数的导数问题,

我们称函数y≡ f(x)本身为它的零阶导数.,dy/dx=f'(x)是f(x)的一阶导数.y=f(x) 的导数称为y=f(x)的二阶导数，记为y"或 f”(x) 或d²y/dx²，二阶导数的导数称为三阶导数，记为y'''或 f'''(x) 或d³y/dx³，一般地,(n-1)阶导数的导数称为n阶导数。当n>3时,记为y(3)或 f(3)(x)或dⁿy/dxⁿ.

二阶及二阶以上的导数都称为高阶导数，函数f(x)的各阶导数在点x=x₀处的数值记为 f'(x₀),f"(x₀),...,f⁽ⁿ⁾(x₀)或y'|x=x₀, y"|x=x₀,…y⁽ⁿ⁾|x=x₀.

求高阶导数就是多次接连地求导数,所以,仍可用前面学过的求导方法来计算高阶导数。

例1：设y=a^x,求y⁽ⁿ⁾(a>0,a≠1).

y'=a^xlna,y''=a^xln²a,一般地,y⁽ⁿ⁾ = a^x Inⁿa(n=1,2,....)

(a^x)⁽ⁿ⁾ = a^x Inⁿa(n=1,2,....)

例2：设y=sinx,求y⁽ⁿ⁾

(sinx)'=cosx=sin(x+π/2);    (sinx)''=-sinx=sin(x+2*π/2);     (sinx)'''=-cosx=sin(x+3*π/2);

一般地, (sinx)⁽ⁿ⁾ = sin (x+ nπ/2)

类似可得(cosx)⁽ⁿ⁾=cos(x+ nπ/2)

例3：设y=sin(ax+b),求y⁽ⁿ⁾

一般地, [sin(ax+b)]⁽ⁿ⁾ = aⁿsin (ax +b+  nπ/2)

类似可得 [cos(ax+b)]⁽ⁿ⁾ = aⁿcos (ax +b+  nπ/2)

例4：设 y= cos⁴x,求 求y⁽ⁿ⁾

cos⁴x=((1+cos2x)/2)²=1/4(1+2cos2x+1/2(1+cos4x))=1/8(3+4cos2x+cos4x)

(cos⁴x)⁽ⁿ⁾=1/8(0+4cos(2x+nπ/2)*2ⁿ+4ⁿcos(4x+nπ/2))=2(n-1)(2x+nπ/2)+2^(2n-3)cos(4x+nπ/2))

 

例5：设y=1/(ax+b),求y⁽ⁿ⁾

(1/(ax+b))'= -a/(ax+b)²

(1/(ax+b))'' = (-a/(ax+b)²)' = 2a²/(ax+b)³

(1/(ax+b))''' = (2a²/(ax+b)³)' = -6a³/(ax+b)⁴

一般的，(1/(ax+b))⁽ⁿ⁾= (-1)ⁿn!aⁿ/(ax+b)ⁿ⁺¹

例6：设y=(ax+b)/(cx+d)(ad-bc≠0,c≠0),求y⁽ⁿ⁾

y=a/c+(bc-ad)/c²*1/(x+d/c),利用上例的结果可得

((ax+b)/(cx+d))⁽ⁿ⁾= (bc-ad)/c²*(-1)ⁿn!/(x+d/c)ⁿ⁺¹

 

例7：设y=In(1+x),求y⁽ⁿ⁾.

(In(1+x))'=1/(1+x),利用例五的结论，

(In(1+x))⁽ⁿ⁾=  (-1)^n-1(n-1)!/(x+1)ⁿ

如果函数 u= u(x) 及 v= v(x) 都在ェ 处具有 n 阶导数,那么有:

(1)[u(x)±v(x)]⁽ⁿ⁾ = u⁽ⁿ⁾(x)±v⁽ⁿ⁾(x);

(2) [cu(x)]⁽ⁿ⁾ = cu⁽ⁿ⁾ (x);

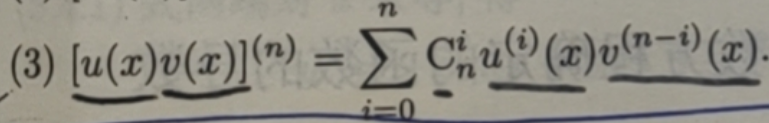
公式(3)称为莱布尼茨公式,C(n,i)是组合数,有兴趣的读者可以运用数学归纳法证明这个公式

例8：设y=x²sinx,求y⁽¹⁰⁰⁾

设u=x²,v=sinx,则u'= 2x, u”=2, u"' =0,...,u⁽¹⁰⁰⁾ =0;

v⁽ⁿ⁾=sin (x+nπ/2)  (n= 0,1,2,·..,100).

代入莱布尼茨公式得

(x²sinx)⁽¹⁰⁰⁾= C(100,0)x²sin (x+100π/2) + C(100,1)2xsin (x+99π/2)  + C(100,2)2sin (x+98π/2) = x²sinx - 200xcosx - 9900sinx

 

4、隐函数的导数

 通常用y=f(x)表示函数关系,能用这种方式表示的函数称为显函数.但有些函数用方程F(x,y)=0给出,也就是变量x与y混在一起难以分开.如果在方程F(x,y)=0中,对于在某非空数集D内的每一个x值,相应地总有满足这个方程唯一的y值与之对应,则称方程 F(x,y)=0在非空数集 D内确定了一个隐函数 y(x),隐函数中的因变量y不一定能用自变量直接表示出来,即不一定能写成y=f(x),这种显函数的形式.

若在 F(ェ,y)=0中确定y是x的函数,要求y',可先将 F(x,y)=0两端对 x求导，在求导过程中视y为的函数(即y是一个中间变量)，求导之后得到一个关于y‘的方程,解此方程便可得y’的表达式,在此表达式中允许含有y,不必(有时也不可能)将y(x)'表示为x的显函数.

 

例1：求由方程e^y+xy-e=0所确定的隐函数y(x)在x=0处的导数

在恒等式e^y+xy-e=0两边都对求导,得 e^yy'+y+xy'=0,解方程y'=-y/(e^y+x)(e^y+x≠ 0).

当x=0时,从所给的方程求得y=1,因此y'|_x=0 =-1/e

例2：求椭圆x²/16+y²/9=1在点(2,3/2√3)处的切线方程。

将椭圆方程的两边对x求导,有8/x+2yy'/9=0,所以y'=-9x/16y,将x=2，y=3/2√3代入上式,得y'|_x=2=-√3/4

于是所求切线方程为y-3/2√3=-√3/4(x-2)

例3：设隐函数为 y= sin(x+y),求 y".

将y=sin(x+y)两端对x求导,得y'= cos(x + y)(x + y)'= cos(x + y)(1 +y'),即y'=cos(x+y)/(1-cos(x+y))

再将y'= cos(x + y)(1 +y')两端对x求导,得y" = - sin(x + y)(1 + y')² + y" cos(x + y),再将y'代入得y"=sin(x+y)/[cos(x+y)-1]³

注在求隐函数的二阶导数的过程中,若整理出二阶导数 y”可用 y',y,x来表示,此时应注意将y‘ 用已求得的y’的关于x,y的表达式替换,即y"的表达式允许含有 x,y,但不应出现 y‘.

 

例4：设x^y=y^x(x>0,y>0),求dy/dx

两边都是幂指函数,故对x^y=y^x两边取对数,得ylnx =xlny.两边对x求导,得y'Inx+y/x=Iny+xy'/y,即dy/dx=y'=y(xlny-y)/x(ylnx-x)

5、由参数方程确定的函数的导数

在实际问题中,函数y与自变量x可能不直接由y=f(x)表示,而是通过一参变量t来确定函数关系,即给定参数方程

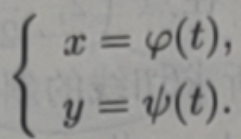如果上式可以确定变量y是x的函数,称此函数为由参数方程所确定的函数。

 设 x=φ (t) 有连续的反函数 t= φ^-1(x),φ(t),ψ(t)都可导,且φ(t)≠0,则由复合函数和反函数的求导法则可得

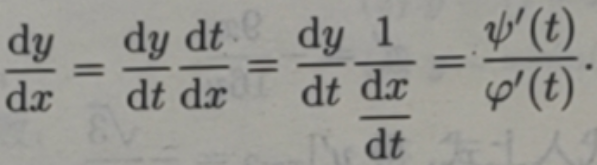这就是由参数方程确定的函数的求导公式.

若x= φ(t),y=ψ(t)二阶可导,在求完一阶导数 后,可设想由参数方程表

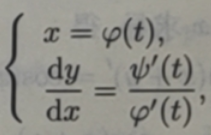
再次应用参数方程求导公式,得

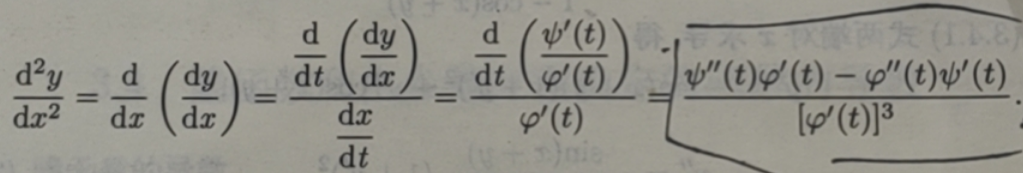
五、微分（近似计算）

1、(函数的)微分

 微分的概念

微分从本质上说是函数增量中关于自变量增量的线性部分，设函数y=f(x)在x处可导,则有有限增量公式Δy = f'(x)Δェ + αΔx,

这里α为当Δx→0时的无穷小,这表明函数的增量Δy可以表示为关于Δx的线性函数(称为 Δy 的线性主部)与较 Δx 高阶的无穷小的和。

因此,当|Δx|较小时,αΔx 可以忽略,即Δy ≈f'(x)Δx

若函数y=f(x)在点x₀处的增量Δy=f(x₀+ Δx)- f(x₀)可以表示为Δx 的线性函数 AΔx(A是与Δx 无关的常数)与较 Δx 高阶的无穷小之和,即Δу =AΔx + o(Δx),则称函数 y= f(x)在点 x₀处可微,并称 AΔ 为函数y= f(x)在点 x₀处的微分,记作dy|x=x₀或 df(x₀).通俗地讲,dy 就是Δy的线性近似

函数 y=f(x)在任意点x的微分,称为函数的微分,记作 dy 或 df(x),即dy = f'(x)Δx.

通常将自变量x的增量记为dx,这相当于y=x的情形,此时显然有dy=dx =Δx.于是微分又可记作dy = f'(x)dx.

若函数 y= f(x) 在点 x 处可微,则 Δy=AΔx+o(Δx),两边除以 Δx,得 Δy/Δx = A + o(Δx)/Δx,于是,当 Δx →0时,可得

因此如果函数y=f(x)在点x处可微,则y≡f(x)在点x处也一定可导,且A =f'(x).

定理 3.5.1函数y= f(x)在点x处可微的充要条件是y=f(x)在点x处可导。

 

函数的微分是函数增量的一部分且它与函数增量只差一个关于自变量增量Ax 的高阶无穷小,因此函数的微分也称为函数增量的线性主部（主要部分).说是“主部”,是因为它与增量之差只是关于 Δx 的一个高阶无穷小;说是“线性”，是因为它是 Δx 的线性(一次)表达式,即 f'(x)Δx.

微分的几何解释

如图3.3所示,设函数y=f(x)在点x₀处可微,因而y=f(x)在点x₀处可导.又设曲线y= f(x)在点 A(x₀,f(x₀))处的切线为 AC,其倾角为α,则函数 y=f(x)在点x₀ 处可微,即dy=f'(x)Δx=AD.tanα=CD.

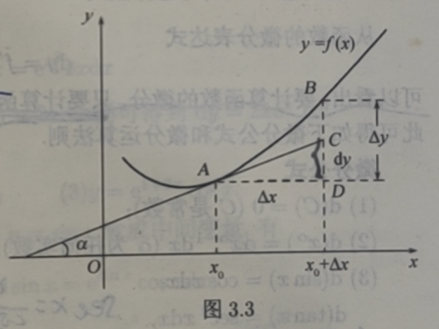
由此可知,曲线y=f(x)在点 A处的切线的纵坐标增量CD 就是函数y=f(x)在点x₀ 处的微分 dy, 而 y= f(x)在点 x₀ 处函数的增量为Δy =f(x₀ + Δx)-f(x₀)= BD.　　

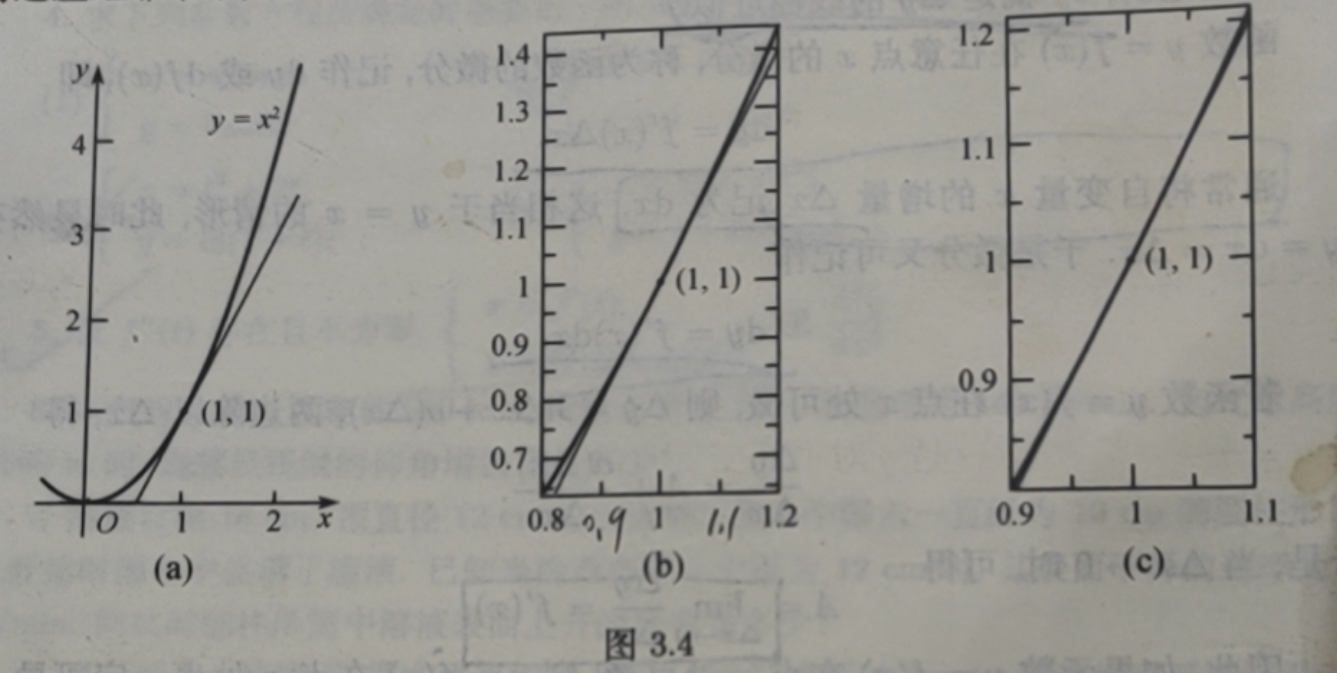
由函数微分的定义可知Δy与dy之差BC是Δx的高阶无穷小,因而在点 A附近的曲线段可用切线段来近似代替.

图3.4是函数y=x²在点x=1处的情形.可以看出微分dy与Δy在x=1附近差距非常小,当 0.9<x<1.1时,如图 3.4(c)所示,dy与Δy几乎看不出差别.

微分基本公式与运算法则

从函数的微分表达式dy = f'(x)dx可以看出,要计算函数的微分,只要计算函数的导数,再乘以自变量的微分即可.由此可得如下微分公式和微分运算法则

微分公式

(1)d(C)=0(C 是常数);

(2)d(x^α)= αx^α-1dx(a 为任何实数);

(3)d(sinx)= cosxdx,   d(cosx)=-sinxdx.    d(tanx)= sec²xdx     d(cotx)=-csc²xdx          d(secx)= secx tanxdx,    d(cscx)=- cscx cotxdx      

(4)d(arcsinx)=-d(arccosx)=1/√(1-x²)dx(|x|<1),     d(arctanx)=-d(arccotx)=1/(1+x²)dx

(5) d(a^x)=a^xInadx(a >0,a≠1),   d(e^x)= e^xdx

(6) d(log_ax)=dx/(xlna)(a>0,a≠1),    d(lnx) = dx/x

微分运算法则

(1) d[u(x)±v(x)] = du(x)± dv(x);

(2) d[u(x)v(x)]= du(x)v(x)+ u(x)dv(x),     d[ku(x)]= kdu(x);

(3) d[u(x)/v(x)] = (du(x)v(x) - u(x)dv(x))/v²(x)    (v(x)≠ 0);

(4)df(g(x))= f’(u)g’(x)dx,其中u= g(x).

徽分运算法则的第(4)式为复合法则,由于 du=g'(x)dx,因此该式也可写成dy = f'(u)du.

由此可见,对函数y=f(x)来说,不论u是自变量还是自变量的可导函数(中间变量),它的微分形式同样都是 dy=f'(u)du,这个性质称为一阶微分形式的不变性。

导数不具备微分的这一特征,因为当u是自变量时,y=f'(u);当u是中间变量u= φ(x) 时,f'(u)仅是y对中间变量u的导数,f'(u)·φ'(x)才是y对x的导数.因此,求函数的导数时,一定要看清是求哪个自变量的导数,

利用一阶微分形式的不变性,还可以求复合函数的导数.

利用微分来求导

例1：求y=sin²(√(1-x²)的导数.

dy = 2sin(√(1-x²) * cos(√(1-x²) * 1/(2√(1-x²)）*（-2x）*dx

dy/dx = -2xsin(√(1-x²) * cos(√(1-x²) /√(1-x²)

例2：求y=sinx对e^x的导数.

dy/de^x =dsinx/de^x=cosxdx/e^xdx=cosx/e^x

例3：设x=acost,y=bsint，求dy/dx

dy/dx=bcostdt/(-asintdt)=-bcost/asint

例4：求xy=e^x+y所确定的函数y对x的导数,

等式两边取微分,得dxy+xdy=e^x+yd(x+y)=e^x+y(dx+dy)

(e^x+y-x)dy=(y-e^x+y)dx    故dy/dx = (y-e^x+y)/(e^x+y-x)

 利用微分进行近似计算

由上面讨论知,微分是函数的线性近似,也就是一个函数在某一点的微小的增量可以用函数在该点的微分来近似.换句话说,函数在其可微点附近可以用一个线性函数来近似,这是一个非常好的性质,因为线性函数是最简单的函数,大家对它已经很了解.这种近似方法无论在工程上还是在数学上都十分有用.

f(x) ≈ f(x₀) + f'(x₀)(x - x₀).

当自变量增量较小时,如果已知函数在某点的导数值和自变量的增量,那么可以用它求得函数增量的近似值;如果还知道该点的函数值,则可算出函数在该点附近的近似值

当x₀=0时,上式就变为f(x) ≈ f(0) + f' (0)x.  

根据这个近似公式及常用微分公式,当|x|很小时,有

sinx≈x, tanx≈x, In(1+x)≈x, e^x≈1+x, (1+x)^1/n≈1+x/n.

 

例1：求sin 29°的近似值.

sin(30-1) = sin(π/6-π/180)，即求f(x)=sinx在x值为π/6,Δx=-π/180时的值f(x)

f(x)≈f(π/6)+f'(π/6)(-π/180)=sin(π/6) + cos(π/6)(-π/180) = 1/2+√3/2*(-π/180)=1/2-√3π/360

例2：求 √26 的近似值.

√26 = √(25+1),即求f(x)=√x在x=25,Δx=1时的函数值，√26≈√25+1/(2√25) = 5.1

 

2、微分中值定理

有了导数之后,就可以用导数来研究函数了.在微分中我们已经看到,在可微点附近函数可以用线性函数来近似,这对研究函数的局部性和进行近似计算很有用.

在这一章我们要建立函数与其导数的等式关系,这便是中值定理.中值定理是联系函数与其导函数的有力工具,可以利用导数在区间上的性质来得到函数在该区间上的整体性质,在数学理论和数学应用上有非常重要的作用.

 费马(Fermat)定理

定义 4.1.1 设函数f(x)在点x₀的某邻域 U(x₀)内有定义,若对任意x∈U(x₀)有f(x)≤ f(x₀)(或f(x)≥ f(x₀)),则称 f(x₀)为函数 f(x)的一个极大值(或极小值),并称点 x₀为f(x)的极大值点(或极小值点).

函数的极大值、极小值统称为极值,极大值点、极小值点统称为极值点

定理 4.1.1(费马定理)若函数f(x)在点x₀处可微,且x₀是f(x)的极值点,则 f'(x₀)=0.

 

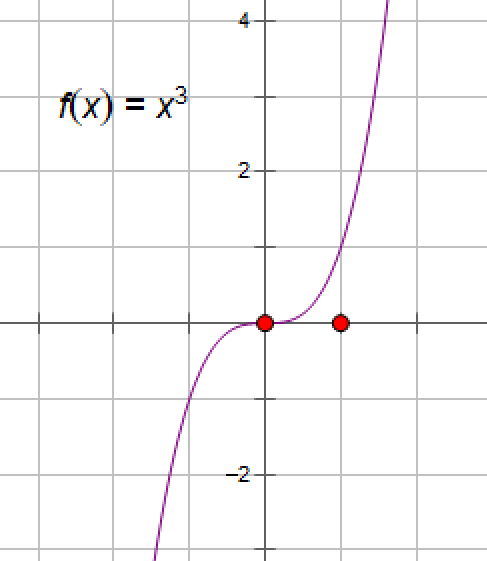
导数为零的点也称为驻点，费马定理告诉我们，极值点如果可导,则一定是驻点。驻点只是可导函数极值点的必要条件,即驻点不一定是极值点:例如,函数y=x³,y'=3x²,在x=0处,y'=0.但显然x=0不是y=x³的极值点.

费马定理的几何解释是:若曲线y=f(x)在极值点有切线,则必为一条水平切线

 

罗尔(Rolle)定理

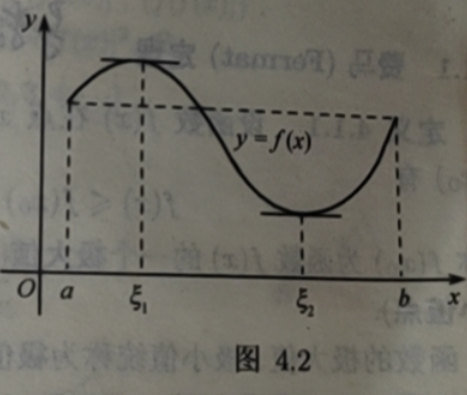
定理 4.1.2(罗尔定理)，若函数f(x)在闭区间[a,b]上续,在开区间(a.b)内可导，且f(a)=f(b),则在(a,b) 内至少存在一点 ξ, 使得 了f'( ξ)=0.

罗尔定理的几何解释是:在平行于x轴的直线所割的光滑曲线段上,至少有一条水平切线(图 4.2)

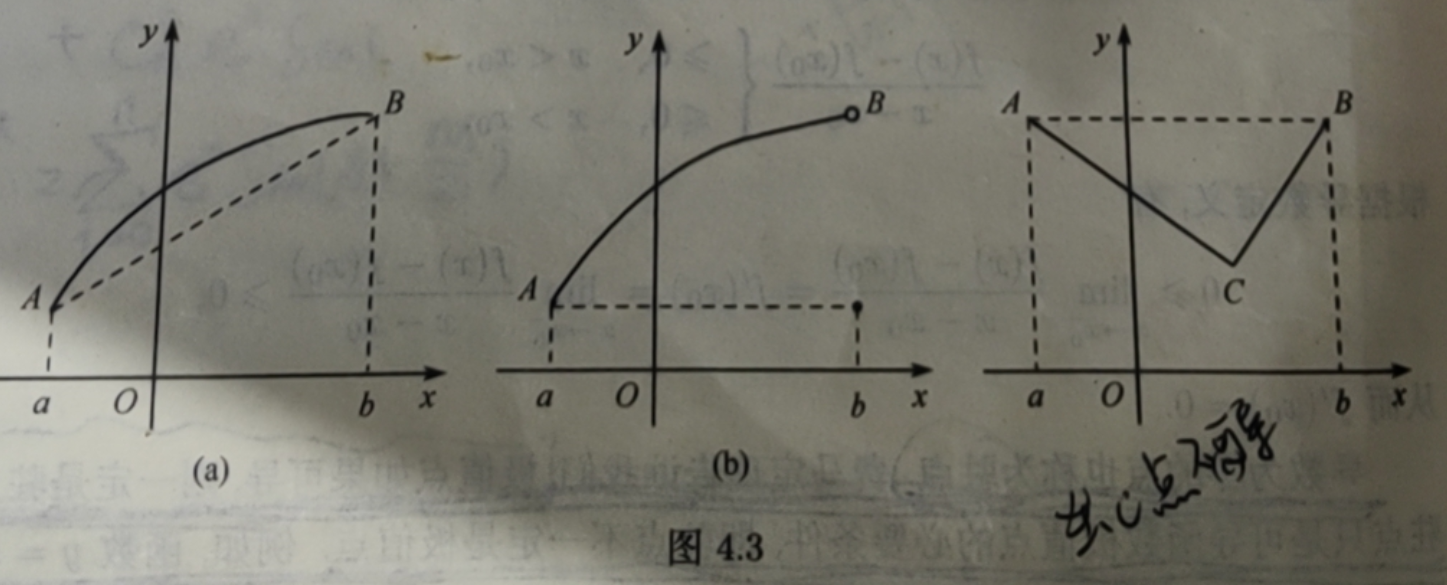
注罗尔定理中的三个条件缺一不可,如果有一个不满足,定理的结论就可能不成立,如图4.3所示

拉格朗日(Lagrange)中值定理

定理 4.1.3(拉格朗日中值定理)若函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,则在(a,b)内至少存在一点ξ,使得f'( ξ) =(f(b) - f(a))/(b-a),称为拉格朗日中值公式，此公式也可以写成f(b)-f(a)=f'( ξ)(b-a)  a<ξ<b

将拉格朗日中值公式与罗尔中值定理相比,发现前者只是去掉了后者的条件f(a)=f(b),将曲线作了一个小变换:将 f(b)往上(或往下)移动 |f(b)- f(a)|的距离.于是就找到了拉格朗日中值公式的证明方法.

拉格朗日中值定理的几何解释是:在直线所割的光滑曲线段上,至少有一点的切线平行于割线

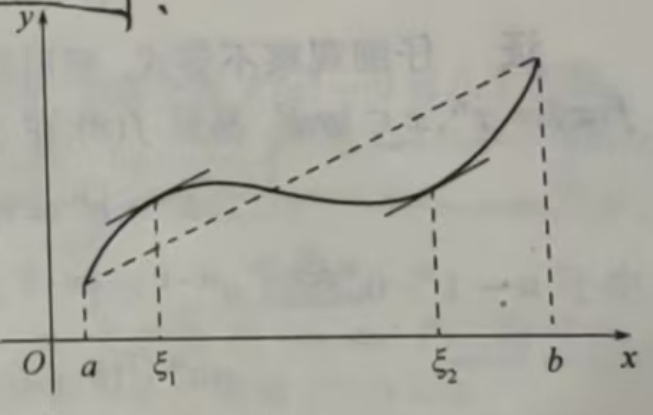
从拉格朗日中值定理可以导出一些有用的推论.

推论1 若在开区间(a,b)内,恒有 f'(x)=0,则 f(x)在(a,b)内恒等于常数.

推论 2 若开区间(a,b)内恒有 f'(x)=g'(x),则在(a,b)内恒有f(x)=g(x)+C (C为常数).

拉格朗日中值定理传递了这样一个信息:当知道了导函数f‘(x)在区间(a,b)内每一点的性质时,就可能得到了函数f(x)在[a,b]上的整体性质.

推论3 如果在闭区间[a,b上连续、在(a,b)内可导的函数f(x)在(a,b)内的导数处处不为零,则 f(a)≠ f(b).

例1：证明恒等式arcsinx+arccosx=π/2, x∈[-1, 1].

已知(arcsinx)'= 1/√1-x²(-1<x<1),(arccosx)'==-1/√1-x²(-1<x<1)，即arcsinx和arccosx的导数相加等于0，由推论1得到arcsinx+arccosx=C，又由于arcsin0+arccos0=π/2,故

arcsinx+arccosx=π/2, x∈[-1, 1],arcsinx和arccosx的函数图像如下：

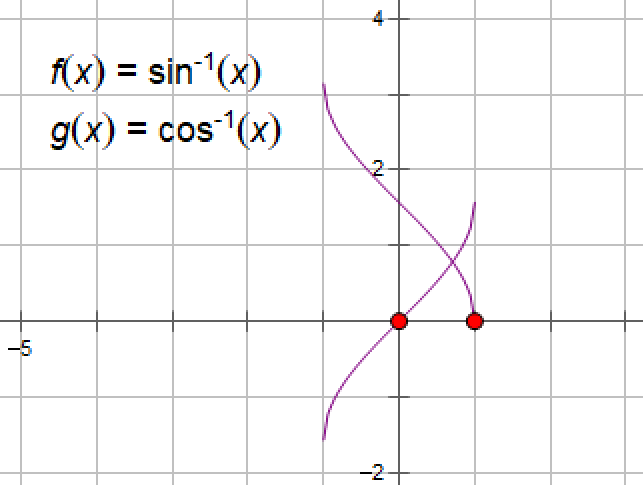
 同理arctanx+arccotx=π/2

例2：设b>a>0,n>1,则有不等式na^n-1(b-a) < bⁿ-aⁿ <nb^n-1(b-a).

仔细观察不等式,要用拉格朗日中值定理,首先要确定用什么函数.设f(x)=xⁿ,x∈[a,b],由于n>1,故函数图像为

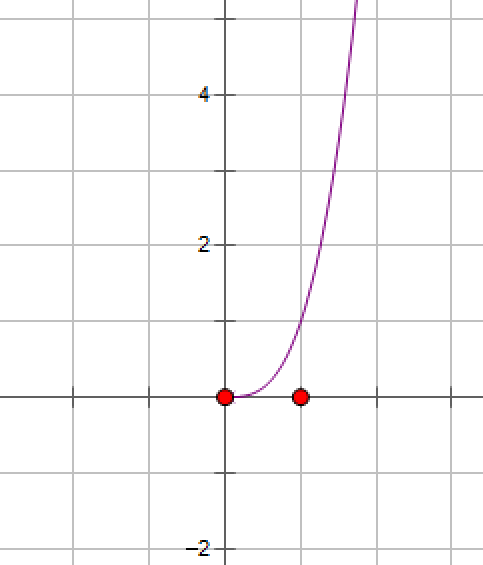
易见 f(x)在[a,b]上满足拉格朗日中值定理的条件(在闭区间[a,b]上连续,在开区间(a,b)内可导),f'(x)=nx^n-1,因此有bⁿ -aⁿ= nx^n-1(b-a), a<x< b.

由于 n-1>0, 所以 a^n-1<x^n-1 <b^n-1.将其代入上式,得na^n-1(b-a) < bⁿ-aⁿ <nb^n-1(b-a).

柯西(Cauchy)中值定理

定理 4.1.4(柯西中值定理)若函数f(x)和g(x)在闭区间[a,b]上都连续,在开区间(a,b)内都可导,且g(x)≠0,则在(a,b) 内至少存在一点ξ,使得f'(ξ)/g'(ξ) = (f(b)-f(a))/(g(b)-g(a))

柯西中值定理可以看成是拉格朗日中值定理的参数方程形式,即y=f(x)由方程所确定

y=f(x)，要求y对x的导数dy/dx=dy/dt*dt/dx=dy/dt*1/(dx/dt)=f'(x)/g'(x)=(f(b)-f(a))/(g(b)-g(a))

罗尔定理、拉格朗日中值定理、柯西中值定理都是存在性定理,即在定理的条件下,保证在开区间(a,b)内至少存在一点ξ满足定理的结论.所谓“中值”是指(a,b)内部的这个点ξ上的导数而言的,定理中并没有指出ξ等于什么,且满足定理结论的ξ也不一定唯一,区间不同,ξ也可能不同,

若在拉格朗日中值定理中增加条件f(a)=f(b),则拉格朗日中值公式就变成f'(ξ)=0.因此罗尔中值定理是拉格朗日中值定理的特殊情形.

又若在柯西中值定理中令g(x)≡x,则柯西中值定理的结论就变成拉格朗日中值公式.因此柯西中值定理是拉格朗日中值定理的推广.

三个中值定理中应用最广的是拉格朗日中值定理,而柯西中值定理在4.2节中有很重要的应用.

 

3、洛必达法则求不定式极限(柯西中值定理的应用)

0/0型和∞/∞型不定式极限

在x的某个变化过程中,如果两个函数f(x)与g(x)都趋于零或者都趋于无穷大,那么极限 limf(x)/g(x)可能存在,也可能不存在,在第2章中曾经遇到过这样的极限,如重要极限x→0时 limsinx/x

。我们把这两种极限称为不定式极限,或直接称为0/0型极限和∞/∞型极限.求这类极限不太容易,下面用柯西中值定理推出求这类极限的一种简单且重要的方法--洛必达法则.

 定理4.2.1(洛必达法则)设

(1) limf(x)/g(x)为0/0型或∞/∞型极限;

(2)在x变化过程中的某时刻以后,f'(x)及 g'(x)都存在,且 g'(x)≠0;

(3) limf'(x)/g'(x)=A(A可为实数,-∞,+∞,∞);

则 limf(x)/g(x)= A.

即两个函数的极限存在（都趋于0或都趋于∞），导数存在，导数比的极限存在，则函数比的极限等于导数比的极限。

例1：x→1时，lim(x²-1)/x-1

这是0/0型不定式极限,应用洛必达法则得

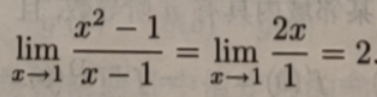
例2：x→+∞时，limlnx/x^a

当x→+∞，limlnx=+∞，limx^a=+∞,(lnx)'=1/x,(x^a)'=ax^a-1

注若imf'(x)/g'(x)仍旧是不定式极限,则只要此极限仍满足洛必达法则条件,就可以再一次应用洛必达法则。

例3：求x→0时lim(e^x-e^-x-2x)/(x - sinx)

 

由于x→0时，lime^x-e^-x-2x = 0,limx-sinx = 0, (e^x-e^-x-2x)'=e^x+e^-x-2,(x-sinx)'=1-cosx,则x→0时,lim(e^x-e^-x-2x)/(x - sinx)=lim(e^x-e^-x-2x)'/(x-sinx)' = lim(e^x+e^-x-2)/(1-cosx)

由于x→0时，lim(e^x+e^-x-2)=0,lim(1-cosx)=0,(e^x+e^-x-2)‘=e^x-e^-x，(1-cosx)’=sinx,则x→0时, lim(e^x+e^-x-2)/(1-cosx) = lim(e^x+e^-x-2)'/(1-cosx)'=lim(e^x-e^-x)/sinx

由于x→0时，lim(e^x-e^-x)=0,limsinx=0,(e^x-e^-x)'=e^x+e^-x，(sinx)'=cosx,则x→0时,lim(e^x-e^-x)/sinx = lim(e^x-e^-x)'/sinx'=lim(e^x+e^-x)/cosx=2

这是0/0型不定式极限,三次应用洛必达法则。

 

例3：x→+∞时，求limx^a/e^x(a>0)

由于x→+∞时，limx^a=+∞,lime^x=+∞,故是∞/∞型的极限。(x^a)'=ax^a-1,(e^x)'=e^x,则根据洛必达法则limx^a/e^x=limax^a-1/e^x.

当0<α≤1时,此极限值为 0;

当α>1时,右端仍是∞/∞型不定式极限，继续应用洛必达法则,直到在分子上第一次出现带有负(或为零)指数为止,而分母则始终是e^x因此,只要α>0,恒有x→+∞时，limx^a/e^x=0

当x→+∞ 时,Inx,x^a(a>0) 和 e^x都是无穷大.但他们趋于无穷大的速度不同,指数函数e^x是比幂函数 x^a 高阶的无穷大,而幂函数x^a 是比对数函数Inx 高阶的无穷大.

当x→+∞ 时，指数函数e^x >幂函数 x^a > 对数函数Inx，limlnx/x^a =0，limx^a/e^x =0，limlnx/e^x=0

其他类型的不定式极限

除 0/0型和 ∞/∞ 型外,不定式极限还有0*∞，∞-∞，0⁰，∞⁰，1^∞ 等类型,一般总可将其化为 0/0型或∞/∞ 型不定式极限,然后再应用洛必达法则。

 

例1：x→0⁺时，lim x^alnx (a >0).

x→0⁺时，limx^a=0,limlnx=-∞,这是0*∞型不定式极限，limx^alnx =limlnx/(1/x^a ) ,由于x→0⁺时，x^a 趋于无穷小，根据“如果 f(x)是无穷小,且f(x)≠0,则1/f(x)是无穷大”的原理，1/x^a 为无穷大，故limlnx/(1/x^a )是∞/∞型的不定式极限，故limlnx/(1/x^a )=lim(1/x)/(-a/x^a+1)=lim-x^a/a=0

例2：x→π/2，求lim(secx-tanx)

lim(secx-tanx) = lim (1/cosx - tanx) = lim (1-sinx)/cosx,当x→π/2时，lim(1-sinx)=0,limcosx=0,根据洛必达法则，故 lim (1-sinx)/cosx=lim (1-sinx)'/cosx'=lim-cosx/-sinx=limcosx/sinx=limcotx=0.

例3：x→0⁺时，求lim(1-cosx)^1/lnx  

x→0⁺时，lim(1-cosx)=0,lim1/lnx=0,这是0⁰型的不定式极限，可以通过指数函数的连续性将幂指函数化为指数函数，然后在指数上应用洛必达法则：

x→0⁺时,lim(1-cosx)^1/lnx =lime^{ln(1-cosx)1/lnx} =lime^{ln(1-cosx)/lnx} ,由于初等函数在其定义域内的区间上连续，故初等函数ln(1-cosx)/lnx也连续。根据前面所学，如果复合函数中的每一层函数都是连续函数,求极限运算可以与函数运算层层交换.

 

当x→0⁺时，limln(1-cosx)=-∞,limlnx=-∞,故是∞/∞型不定式极限。所以lime^{ln(1-cosx)/lnx} =lime^{ln(1-cosx)‘/(lnx)'} 

=lime^{xsinx/(1-cosx)} ,由于x→0⁺时，limxsinx=0,lim(1-cosx)=0,故是0/0型的，lime^{xsinx/(1-cosx)} =lime^{(xsinx)'/(1-cosx)'} = lime^{(sinx+xcosx)/sinx} ,由于x→0⁺时，lim(sinx+xcosx)=0,limsinx=0,

故是0/0型的，所以lime^{(sinx+xcosx)/sinx} =lime^{(sinx+xcosx)‘/(sinx)'} =lime^{(2cosx-xsinx)/cosx} 

 

由于外层函数e^x 在x→0⁺时连续，(2cosx-xsinx)/cosx在x→0⁺时连续，故lime^{(2cosx-xsinx)/cosx} =e^{lim(2cosx-xsinx)/cosx} =e²

 

 

例4：x→+∞时，求limx^1/x

limx^1/x =lime^lnx/x ,x→+∞时,limlnx=∞,limx=∞,故lime^lnx/x =lime^(lnx)'/x' =lime^1/x =e⁰ =1

例5： x→1时，求limx^1/(1-x) 

limx^1/(1-x) =lime^lnx/(1-x) =lime^{(lnx)'/(1-x)'} =lime^-1/x =e^-1 = 1/e

运用洛必达法则,应注意以下几点:

(1)每次运用洛必达法则之前均应检查是否满足洛必达法则的条件,否则就可能出错.

例6：x→0时，求lim(e^x-cosx)/xsinx

x→0时，lim(e^x-cosx) = 0,limxsinx=0,故是0/0型的。lim(e^x-cosx)/xsinx=lim(e^x-cosx)’/(xsinx)'=lim(e^x+sinx)/(sinx+xcosx).由于x→0时，lim(e^x+sinx)=1,lim(sinx+xcosx)=0,故不是0/0型的，不能用洛必达法则。根据函数的极限运算，lim(e^x+sinx)/(sinx+xcosx)=lim1/0=∞,即无穷小的导数为无穷大。

 

(2)洛必达法则的条件是充分的,不是必要的,因此运用洛必达法则不能解决某不定式极限问题时,并不意味着所求极限不存在,仅表明洛必达法则对此失效,请看下例.

例7：x→∞时，求lim(x+sinx)/x

x→∞时，lim(x+sinx)=∞,limx=∞,这是∞/∞型的，故lim(x+sinx)/x = lim(x+sinx)‘/x‘ = lim(1+cosx),极限不存在,所以此题不能应用洛必达法则

lim(x+sinx)/x=lim(1+sinx/x)/1=(1+0)/1=1

(3)使用洛必达法则时,极限 limf'(x)/g'(x)应比极限 limf(x)/g(x)容易计算，否则就失去了洛必达法则的意义

例7：

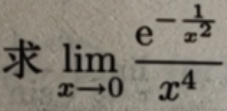
若将此。型不定式极限直接应用洛必达法则,则有

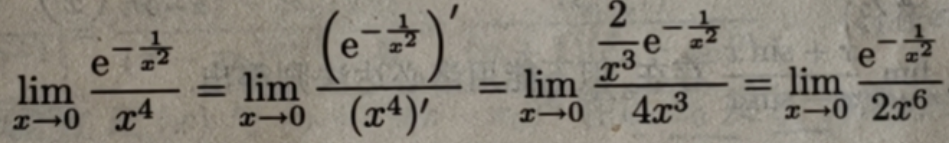
这比原来的极限更复杂,无助于问题的解决.

令1/x²=y,则x→0时，y→∞。故原式等于lime^(-y) *y²  =limy² /e^y ,由于y→∞时，limy²=∞,lime^y = ∞,故是∞/∞型的，limy² /e^y =lim2y/e^y ,由于y→∞时，lim2y=∞,还是是∞/∞型的，lim2y/e^y =lim2/e^y =0

(4)在用洛必达法则求不定式极限的过程中,还可结合使用其他求极限的有效方法,如等价无穷小代换,使计算更简化.

例8：x→0时，lim(e^x+e^-x-2)cosx/sinx(e^x-1)

这是0/0型不定式极限,若直接用洛必达法则,会使计算很烦琐.但若先用等价无穷小量x将分母中的 sinx,(e^x-1)替换掉,并将x→0时cosz的极限单独计算出来,再利用洛必达法则计算就较为简便了

x→0时，lim(e^x+e^-x-2)cosx/sinx(e^x-1) = limcosx*lim(e^x+e^-x-2)/x² ,x→0时，lim(e^x+e^-x-2)=0,limx²=0,故是0/0型的，lim(e^x+e^-x-2)/x² =lim(e^x+e^-x-2)'/(x²)' =lim(e^x-e^-x)/2x =lim(e^x+e^-x)/2 = 1

4、泰勒公式求极限（用多项式来代替函数在某点的值）

　　泰勒公式在数学、物理、工程等领域有着广泛的应用，主要用于近似计算和函数分析。泰勒公式是一个用函数在某点的信息描述其附近取值的公式。它通过已知函数在某一点的各种导数值来构建一个多项式，这个多项式可以用来近似函数在这一点的邻域中的值。在数学中，泰勒公式用于近似计算和函数分析。通过泰勒展开，可以将复杂的函数表示为简单的多项式形式，从而简化计算和分析过程。

　　对于一些较复杂的函数,为了便于研究,往往希望用一些简单的函数来近似它由于多项式是除线性函数外最简单的一种函数,因此用多项式来逼近函数是十分自然的想法.

在学习微分时已经知道,当函数f(x)在x₀可微时,在x₀附近可以用一个线性函数 f(x₀)+f'(x₀)(x-x₀)来近似f(x),其误差是关于(x-x₀)的高阶无穷小,但这还不够.现在的问题是:如果函数f(x)在含有x₀的开区间内具有(n+1)阶导数,如何找出一个关于(x-x₀)的n次多项式

如果 f(x)与Pn(x)在x=x₀ 处具有相同的直到n阶的导数f^(k)(x₀)=Pn^(k)(x₀),k=0,1,…..,n,而Pn^(k)(x₀)=a_kk!,这样就可得

a_k=Pn^(k)(x₀)/k!=f^(k)(x₀)/k!

下面的定理表明,这样确定的多项式就是所要我的多项式.

泰勒中值定理

定理 4.3.1(泰勒中值定理)设函数f(x)在点 x₀ 的某个邻域 U(x₀)内(n+1)阶可导,则在此邻域内有

f(x)=f(x₀)+f'(x₀)(x-x₀)+f''(x₀)(x-x₀)²/2!+...+f⁽ⁿ⁾(x₀)(x-x₀)ⁿ/n!+f⁽ⁿ⁺¹⁾(ξ)(x-x₀)ⁿ⁺¹/(n+1)!    (4.3.1)

其中ξ是介于x₀与x之间的某个值.

泰勒公式是一个用函数在某点的信息描述其附近取值的公式。

证明：设Rn(x)=f(x)-[f(x₀)+f'(x₀)(x-x₀)+f''(x₀)(x-x₀)²/2!+...+f⁽ⁿ⁾(x₀)(x-x₀)ⁿ/n!]

Rn(x₀) = f(x₀)-f(x₀)，R'n(x)=f'(x)-[f'(x₀)+f''(x₀)(x-x₀)+...+f⁽ⁿ⁾(x₀)n(x-x₀)^n-1/n!]，故R'n(x₀)=0，

R'‘n(x)=f'’(x)-[f''(x₀)+...+f⁽ⁿ⁾(x₀)n(n-1)(x-x₀)^n-2/n!],故R''n(x₀)=0,定理,得

R⁽ⁿ⁾n(x)=f⁽ⁿ⁾(x)-[f⁽ⁿ⁾(x₀)n!/n!]，故R⁽ⁿ⁾n(x₀)=0

对两个函数 Rn(x)和(x-x₀)ⁿ⁺¹,在以x₀及x为端点的区间上应用柯西中值定理,得

Rn(x)/(x-x₀)ⁿ⁺¹ =[Rn(x)-Rn(x₀)]/[(x-x₀)ⁿ⁺¹ -0]=R'n(ξ₁)/(n+1)(ξ₁-x₀)ⁿ   (ξ₁在x₀与x之间)

再对两个函数R’n(x)与(n+1)(x-x₀)ⁿ 在以x₀及ξ₁ 为端点的闭区间上应用柯西中值定理,得

R'n(ξ₁)/(n+1)(ξ₁-x₀)ⁿ =[R'n(ξ₁)-R'n(x₀)]/[(n+1)(ξ₁-x₀)ⁿ -0]=R''n(ξ₂)/(n+1)n(ξ₂-x₀)^n-1 (ξ₂在x₀及ξ₁之间).

如此做下去,经(n+1)次后,得

 Rn(x)/(x-x₀)ⁿ⁺¹ = R⁽ⁿ⁺¹⁾n(ξ)/(n+1)!   (ξ在x₀与ξ_n之间,因而也在x₀与x之间).

由Rn(x)的定义可知R⁽ⁿ⁺¹⁾n(ξ)= f⁽ⁿ⁺¹⁾(ξ),于是 

Rn(x)= f⁽ⁿ⁺¹⁾(ξ)(x-x₀)ⁿ⁺¹ /(n+1)!  (4.3.2)

公式(4.3.1)称为 f(x)按(x-x₀)的幂展开的n阶泰勒公式. Rn(x)的表达式 (4.3.2)称为拉格朗日余项

当 f⁽ⁿ⁺¹⁾(x) 有界,x→ x₀ 时 Rn(x)是(x-x₀)ⁿ的高阶无穷小.

当不需要余项的精确表达式时,n 阶泰勒公式也可写成

f(x)=f(x₀)+f'(x₀)(x-x₀)+f''(x₀)(x-x₀)²/2!+...+f⁽ⁿ⁾(x₀)(x-x₀)ⁿ/n!+o[(x-x₀)ⁿ ]    

这里o[(x-x₀)ⁿ ] 称为皮亚诺余项,虽然皮亚诺余项没有拉格朗日余项精确，但n阶带有皮亚诺余项的泰勒公式只要求f(x)具有n阶导数.(言外之意：n阶带有拉格朗日余项的泰勒公式要求f(x)具有n+1阶导数)

证Rn(x)是(x-x₀)ⁿ的高阶无穷小：

设Rn(x)=f(x)-[f(x₀)+f'(x₀)(x-x₀)+f''(x₀)(x-x₀)²/2!+...+f⁽ⁿ⁾(x₀)(x-x₀)ⁿ/n!]

易见 Rn(x₀)=R'(x₀)=···=R⁽ⁿ⁾(x₀)=0.反复应用洛必达法则,有

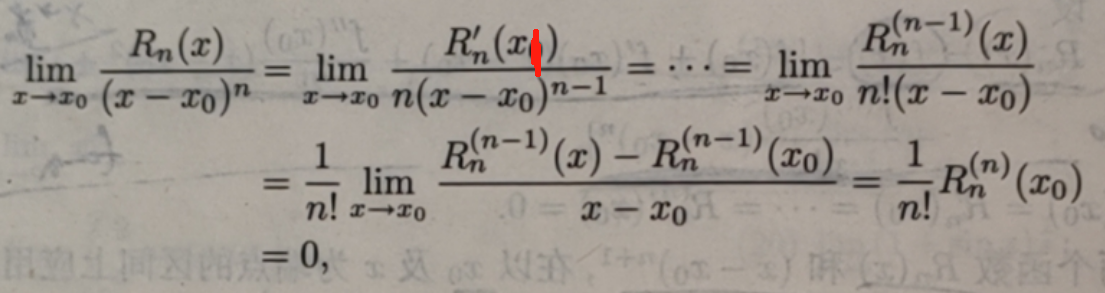
注意这里最后是用导数的定义得到R⁽ⁿ⁾n(x₀)/n!的.

几个初等函数的带皮亚诺余项的麦克劳林(Maclaurin)公式

x=0处的泰勒公式称为麦克劳林公式,下面是几个常见的初等函数的带皮亚诺余项的麦克劳林公式.

麦克劳林公式是函数在某一点（这里是x=0）附近的近似表达式，通过函数的导数信息来构建。

注意：带有皮亚诺余项说明只需要n阶可导即可

（1）、f(x)=e^x 

因为 f^(k)(x) =e^x ,故 f^(k)(0)=1  ,k=0,1,2,…,从而

e^x  = 1+x+x²/2!+x³/3!+...+xⁿ/n!+o(xⁿ)

（2）、f(x)=sinx 

因为f^(k)(x) = sin (x+kπ/2),故f^(2m)(0)=0,f^(2m+1)(0)=(-1)^m ,m=0,1,2,,从而

sin(x)=x-x³/3!+x⁵/5!+...+(-1)^m x^2m+1 /(2m+1)! +o(x^2m+2)

（3）、f(x)=cosx 

由 f^(k)(x) = cos (x+kπ/2),得f^(2m+1)(0)=0,f^(2m)(0)=(-1)^m ,m=0,1,2,,从而

cos(x)=1-x²/2!+x⁴/4!+...+(-1)^mx^2m/(2m)!+o(x^2m+1) 

（4）、f(x)=ln(1+x)

由f^(k)(x) =  (-1)^k-1(k-1)!/(x+1)^k得f(0)=0,f^(k)(0)=(-1)^k-1(k-1)!, k=1,2,…,从而

ln(1+x)=x-x2/2+x3/3+...+(-1)n-1xn/n+o(xⁿ)

（5）、f(x)=(1+x)^α 

易得f(0)=1及 f^(k)(0)=α(α-1)…(a-(k-1)),k=0,1,2,,从而

(1+x)^α =1+αx+α(α-1)x²/2+....+α(α - 1)··(α -(n- 1))xⁿ /n!+o(xⁿ)

对于上述麦克劳林公式,读者可以自己写出相应的带拉格朗日余项的麦克劳林公式.

带皮亚诺余项的麦克劳林公式常可用来计算极限，当一个问题中涉及函数的高阶导数时,也常用泰勒公式来解决.

例1：x→0时，求lim(cosx-e^-x2/2 )/x⁴

由于分母只有4次方，故带皮亚诺余项的麦克劳林公式只需要精确到x⁴即可

因为cos(x)=1-x²/2!+x⁴/4!+o(x⁴)，e^-x2/2 = 1+(-x²/2)+(-x²/2)²/2!+o(x⁴) = 1-x²/2+x⁴/8+o(x⁴)

lim(cosx-e^-x2/2 )/x⁴=lim[1-x²/2+x⁴/24-(1-x²/2+x⁴/8)+o(x⁴)]/x⁴ =[-x⁴/12+o(x⁴)]/x⁴ =-1/12

例2：x→+∞时，求lim(x³+3x²)^1/3-(x⁴-2x³)^1/4 

x→+∞,则1/x趋向于0，故可以使用麦克劳林公式。

由于(1+x)^α =1+αx+α(α-1)x²/2+....+α(α - 1)··(α -(n- 1))xⁿ /n!+o(xⁿ)

(x³+3x²)^1/3=x(1+3/x)^1/3 = x(1+1/x+o(x^-2)) = x+1+o(x^-1)

(x⁴-2x³)^1/4 =x(1-2/x)^1/4 = x(1-1/(2x)+o(x^-2)) = x-1/2 + o(x^-1)

x→+∞时，lim(x³+3x²)^1/3-(x⁴-2x³)^1/4 =lim x+1+o(x^-1) - (x-1/2 + o(x^-1)) = 3/2

泰勒公式使得可以用多项式Pn(x-x₀)来近似代替函数f(x),并且当x→x₀时，这种近似产生的误差是(x-x₀)ⁿ的高阶无穷小,于是,能把较复杂的函数f(x)的研究化为一个关于(x-x₀)的n次多项式的研究.一般地,n越大,用Pn(x-x₀)代替f(x)的近似程度越好,其误差是拉格朗日型余项Rn(x)= f⁽ⁿ⁺¹⁾(ξ)(x-x₀)ⁿ⁺¹ /(n+1)! ,但因不知ξ的确切位置,误差该如何计算呢?实际上,只要能估计出|f⁽ⁿ⁺¹⁾(ξ)|<M(M为常数),就有

因而取M|x-x₀|ⁿ⁺¹/(n+1)!作为 P(x-x₀)代替f(x)所产生的误差.因此,泰勒公式解决了近似表达式中的误差估计问题.

例3:求√37的近似值

√37=6(1+1/36)^1/2 ,故f(x)=(1+x)^1/2 ，x=1/36,即x→0,故可以用麦克劳林公式。

x在U(0)的邻域内有(1+x)^α =1+αx+α(α-1)x²/2+....+α(α - 1)··(α -(n- 1))xⁿ /n!+o(xⁿ)，

(√(x+1))'=1/2(x+1)^-1/2 ,(√(x+1))''=(1/2(x+1)^-1/2 )'=-1/4(x+1)^-3/2 ,(√(x+1))'''=(-1/4(x+1)^-3/2 )'=3/8(x+1)^-5/2 ,故拉格朗日余项为3/8(1+ξ)^-5/2 *(1/36)³ /3!=1/16*(1+ξ)^-5/2 *(1/36)³ 其中ξ∈(0,1/36)，由于(1+ξ)^-5/2 <1,所以1/16*(1+ξ)^-5/2 *(1/36)³ <1/16*(1/36)³ ，即拉格朗日余项都比1/16*(1/36)³ 还要小,故将1/16*(1/36)³作为误差进行舍弃。

√37=6(1+1/36)^1/2 =6(1+1/2*1/36+1/2*(1/2-1)(1/36)² /2 +1/2*(1/2-1)*(1/2-2)(1/36)³ /6 +o((1/36)ⁿ) ) < 6(1+1/2*1/36 -1/8*(1/36)² +1/16*(1/36)³ +1/16*(1/36)³)≈6(1+1/2*1/36 -1/8*(1/36)² )= 6.08275

5、函数的单调性、极值和最值(拉格朗日中值定理的应用)

运用导数研究函数性质是导数应用的一个重要方面,通常所说的函数性态,主要包括单调性、极值、最值、函数图形的凸性、拐点、渐近线等,.本节利用拉格朗日中值定理导出用函数的导数来判定函数的单调性、极值和最值的方法.

函数的单调性的判别法

定理 4.4.1 设函数 f(x)在[a,b]上连续,在(a,b)内可导.若在(a,b)内恒有f'(x)>0 (或<0),则 f(x)在[a,b]上严格单调增加(或严格单调减少).

定理 4.4.1的几何意义是:若函数f(x)在某区间上图形的切线与x轴的夹角a 是锐角 (tana > 0,f'(x)= tana),则函数在该区间上严格单调增加;若这个夹角a是钝角(tana<0),则函数在该区间上严格单调减少

值得注意,f'(x)>0是 f(x)严格单调增加的充分条件,并非必要条件.例如f(x)= x³,在(-∞,+∞)上单调增加,但 f'(0)=0.事实上,若f(x)的导数只在有限多个点处为零,其余各处都大于零(或小于零),就可得f(x)是严格单调增加(或严格单调减少)的.

若要确定函数 f(x)的单调区间,可先在f(x)的定义域内找出所有 f(x)的不可导点和驻点.用这些点将f(x)的定义域分成若干个小区间,在每个小区间上确定f'(x)的符号,然后根据定理 4.4.1,确定f(x)在每个小区间上的单调性.

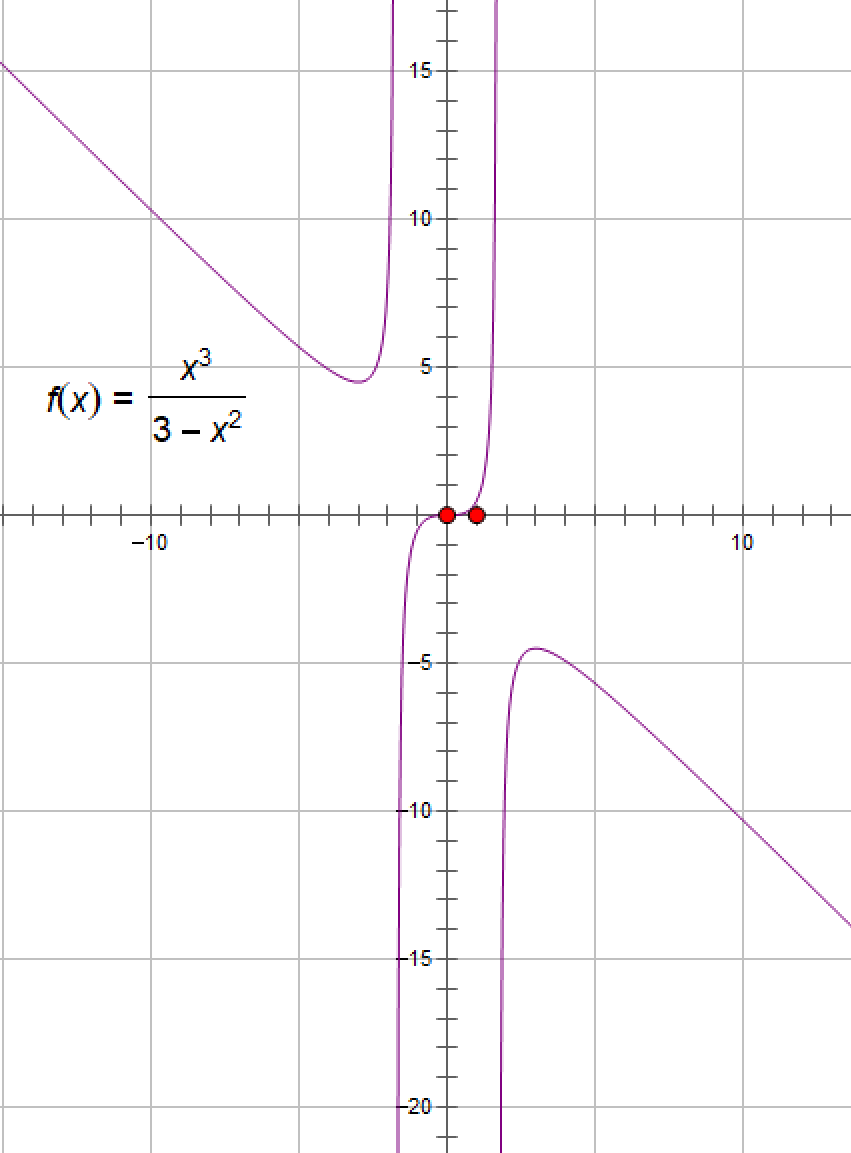
例1：确定函数 f(x)=x³/(3-x²)的单调区间.

f(x)的定义域为(-∞,-√3)U(-√3,√3)U(√3,+∞),f'(x)=[3x²(3-x²)-x³(-2x)]/(3-x²)² =x²(3-x)(3+x)/(3-x²)² ,所以 f(x)有三个驻点:x1=-3,x2=0,x3=3.用这些驻点和-√3,√3将定义域分成6个区间,如表 4.1 所示.

 因此，f(x)在(-∞,-3],[3,+∞)上严格单调减少,在 [-3,-√3),(-√3,√3),(√3,3]上严格单调增加.

函数图像如下：

应用函数的单调性还可以证明不等式.

例2：证明:当x>0时,1+xIn[(x+√(1+x²)]>√(1+x2)

令f(x)=1+xIn[(x+√(1+x²)]-√(1+x²),函数f(x)在[0,+∞)上连续且f'(x)=In[(x+√(1+x²)],由于x>0,故(x+√(1+x²)>1,所以f'(x)>0.故函数f(x)在x>0时单调递增。f(0)=0,所以x>0时f(x)=1+xIn[(x+√(1+x²)]-√(1+x²)>0,故当x>0时,1+xIn[(x+√(1+x²)]>√(1+x2)

函数的极值的判别法

由费马定理,可导函数的极值点必是驻点，因此,驻点和导数不存在的点是极值点的必要条件,但驻点和不可导点是否是极值点还需进一步判定,定理 4.4.2就是利用函数的单调性来判定函数的极值.

即极值点能推出该点是驻点或导数不存在的点，但是驻点不一定能判断是极值点，如f(x)=x³ 

定理 4.4.2(极值点的第一充分条件)设函数f(x)在点 x₀的某邻域 U(x₀;δ)内连续,在空心邻域 U°(x₀;δ)内可导.若函数f(x)满足:(1)在(x₀ -δ,x₀)内 f'(x)>0(或<0);(2)在(x₀,x₀+δ)内f'(x)<0(或>0)

则f(x)在点x₀处取得极大值(或极小值).

求函数的极值,一般可先求出函数的驻点和不可导点，然后考察这些点两侧导数的符号,再运用定理4.4.2找出极值点,并计算出极值.

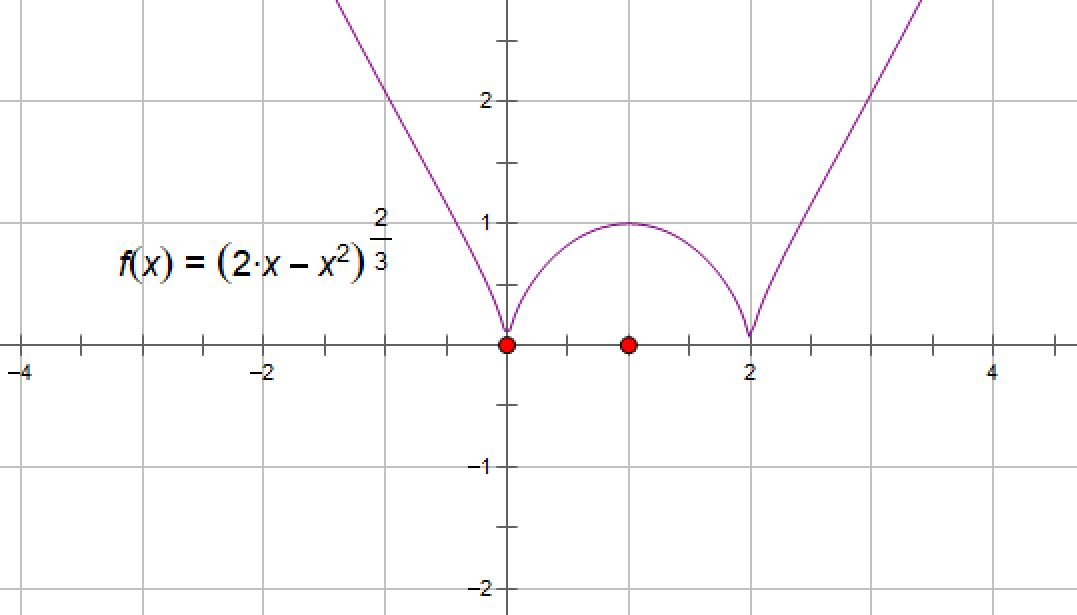
例1：求f(x)=(2x-x²)^2/3 的极值点和极值.

函数在(-∞,+∞)上连续,且f'(x)=4(1-x)/3(2x-x²)^1/3 ,当x=1时，f'(x)=0,可知 f(x)的驻点为 x=1,

y=x^1/3 的函数图像可知，当x<0时，f'(x)<0,当0<x<1时，f'(x)>0，当1<x<2时，f'(x)<0，当x>2时，f'(x)>0。可知导函数f'(x)<0在x=0和x=2两侧的符号不同，故在这两点肯定不可导

所以x=1为f(x)的极大值点，极大值f(1)=1,x=0和x=2为f(x)的极小值点，极小值f(0)=0，f(2)=0

函数图像如下:

定理4.4.2的条件是充分的但非必要的,如函数

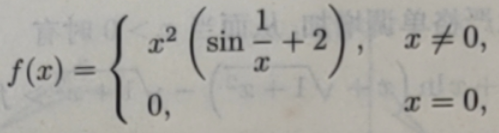
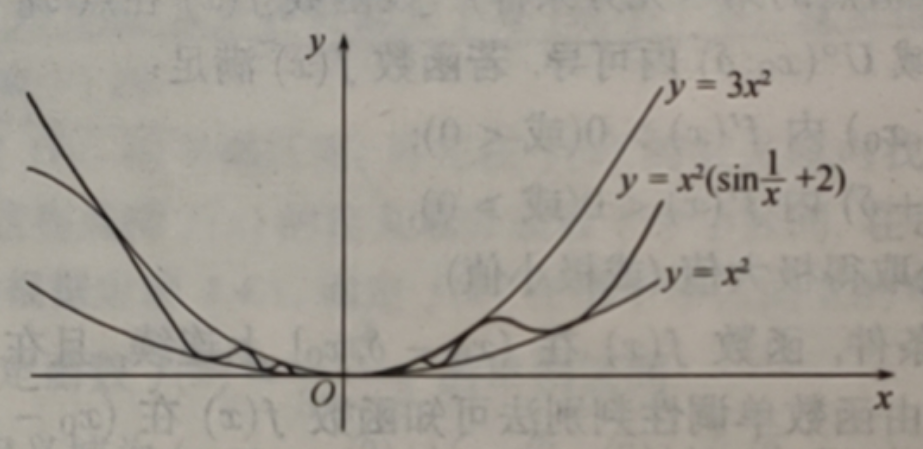
根据无穷小与有界变量的乘积仍是无穷小的原理，x→0时，f'(0)=lim[x²(sin1/x +2) - 0 ]/(x-0) = limx(sin1/x + 2) = 0.即一阶导数值为0

x≠0时,f'(x)=2x(sin1/x+2)-cos1/x

可见,不存在δ>0,使得 f'(x)在(-δ,0)和(0,δ)内异号.但x²≤x²(sin1/x+2)≤3x²,所以f(0)=0是所给函数的极小值

当函数 f(x)在驻点处的二阶导数存在且不为零时,有如下的极值判定定理

定理 4.4.3(极值点的第二充分条件)设函数f(x)在点x₀处二阶可导,且f'(x₀)= 0,f"(x₀)>0(< 0)，则f(x)在点x₀处取极小值(或极大值).

证  由二阶导数定义有

x→x_0时，f''(x₀)=lim[f'(x)-f'(x₀)]/(x-x₀)=limf'(x)/(x-x₀)>0,根据函数极限的局部保号性,存在x₀的空心邻域 U°(x₀),在U°(x₀)内恒有f'(x)/(x-x₀)>0

因此,当x<x₀ 时,f'(x)<0; 当 x>x₀ 时,f(x)>0.由定理 4.4.2知x₀是f(x)的极小值点.

 

例1：求f(x)=x³-9x²+15x+3的极值.

因为f'(x)=3(x-1)(x-5),得驻点x=1和x=5.又f"(x)=6x-18=6(x-3),f"(1)= -12 <0, f"(5)= 12 >0,故在x=1处为极大值，在x=5处为极小值。函数图像如下：

需要注意的是,若f“(x₀)=0,f"(x₀)=0,则不能判定f(x)在x₀处是否取得极值.例如设f1(x) = x⁴,f2(x)=-x⁴,f3(x)=x³,则此三函数在x=0处的一阶、二阶导数都为零.但f1(0)=0为极小值,f2(0)为极大值,f3(0)不是极值.

函数的最值

最大(小)值通常是指在所讨论的整个区间上函数值的最大值或最小值.与极值不同,极值是一个局部性(某邻域内)的概念,而最值是一个整体性(区间上)的概念

如何寻求连续函数在闭区间[a,b]上的最值呢?首先,如果最值在区间内部某点x₀取得,容易得到x₀也是极值点.因此,或x₀是驻点,或在x₀点导数不存在.当然最值也可能在端点取得.总之,函数在闭区间[a,b]上的最值点只能在驻点，不可导点、区间的端点上取得,因此这三类点的函数值中的最大(小)者即为函数在[a,b]上的最大(小)值.

例1：求函数 f(x)=(2x-5)x^2/3 在闭区间[-1,5/2]上的最大值和最小值

由于f'(x)=10(x-1)/3x^1/3 ,可知x=0是f(x)的不可导点,x=1是f(x)的驻点，在这些点和区间端点的函数值分别为f(0)=0,f(1)=-3, f(-1)=-7,f(5/2)=0,故函数f(x)在[-1,5/2]上的最大值是0,最小值是 -7.

一个可微函数如果在定义区间内只有一个驻点,那么可以用函数该驻点的值与在定义区间端点的值(或左右极限值)进行比较来判定该驻点是否为最大值或最小值,许多实际问题就是这种情况,当然,如果可以根据问题的实际意义断定函数在定义区间内确有最大值或最小值,那么这个唯一的驻点就是最大值点或最小值点

6、函数图形的讨论

曲线的凸性与拐点

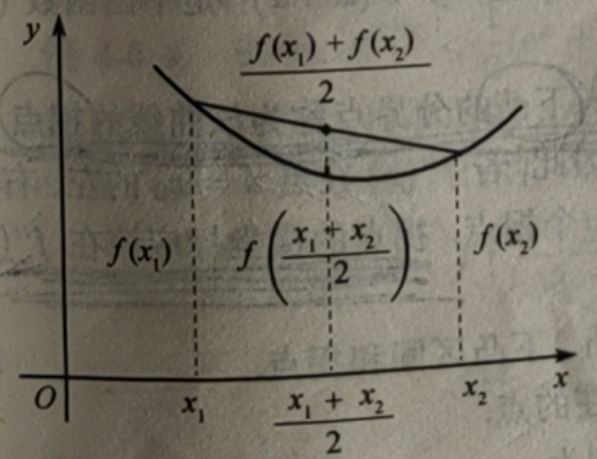
前面已经讨论了函数图形的单调性,但是单调性还不能很好地反映函数及其图形的形态,因此本节要讨论函数图形的凸性.如果任意作一条曲线的弦,曲线总是在弦的下方,则曲线表现为下凸的;若任意作一条曲线的弦,曲线总是在弦的上方,则曲线表现为上凸的.下面给出的就是上述曲线凸性的一个等价定义.

定义4.5.1设f(x)在区间I上连续,如果对I上的任意两点 x₁,x₂恒有

则称函数f(x)在I上是下凸的函数,或称f(x)的图形y=f(x)在I上是下凸曲线.

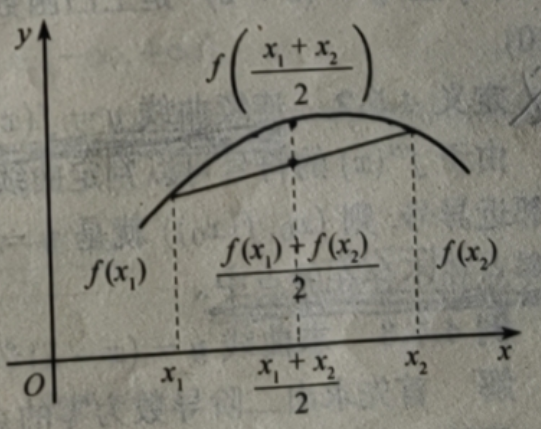
如果恒有

则称函数 f(x)在I上是上凸的函数,或称f(x)的图形y=f(x)在I上是上凸曲线

定理 4.5.1 若函数 f(x)在[a,b]上连续,在(a,b)内有二阶导数,且 f"(x)>0(或< 0), 则曲线 y= f(x)在[a,b]上是下凸(或上凸)的.

例1：讨论函数y=e^x+1的凸性.

 因为 y'' =e^x+1 >0, 所以函数 y=e^x+1 在其定义域(-∞,+∞) 上是下凸函数

并不是每个函数在其定义域中非上凸即下凸,由定理 4.5.1,二阶导数的符号决定了函数的凸性，

例2：讨论函数y=(x-2)³的凸性

因为 y“= 6(x- 2),当x<2 时,y"<0;x>2时,y">0.因此在区间(-∞,2] 上,y=(x-2)³是上凸函数;在[2,+∞)上，y=(x-2)³是下凸函数.

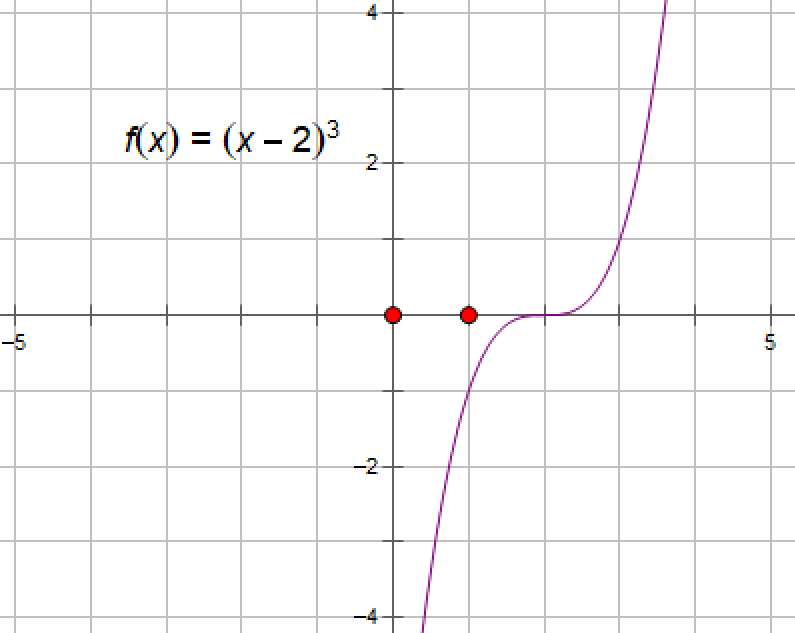
定义4.5.2 连续曲线y=f(x)的上凸与下凸的分界点称为该曲线的拐点。

由于 f"(x)的符号可以判定曲线的凸性,因此,若f"(x)在点x=x₀的左、右两侧邻近异号,则(x₀,f(x₀))就是y=f(x)的一个拐点.拐点的横坐标应该在f”(x)的零点和不存的点中。

 

例1：求曲线y=(x-1)x^3/5 的上凸、下凸区间和拐点.

首先求出二阶导数为零的点和不存在的点.函数y=(x-1)x^5/3的一、二阶导数分别为

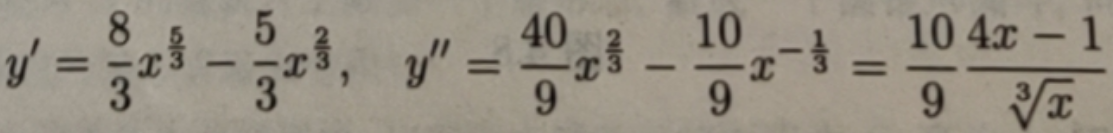
y'=8/3x^5/3-5/3x^2/3,y''=40/9x^2/3-10/9x^-1/3 = 10(4x-1)/9x^1/3

在x=0处y"不存在,在x=1/4处y"=0.用点x=0,x=1/4把定义域(-∞,+∞)分成几个小区间,如表 4.4 所示.

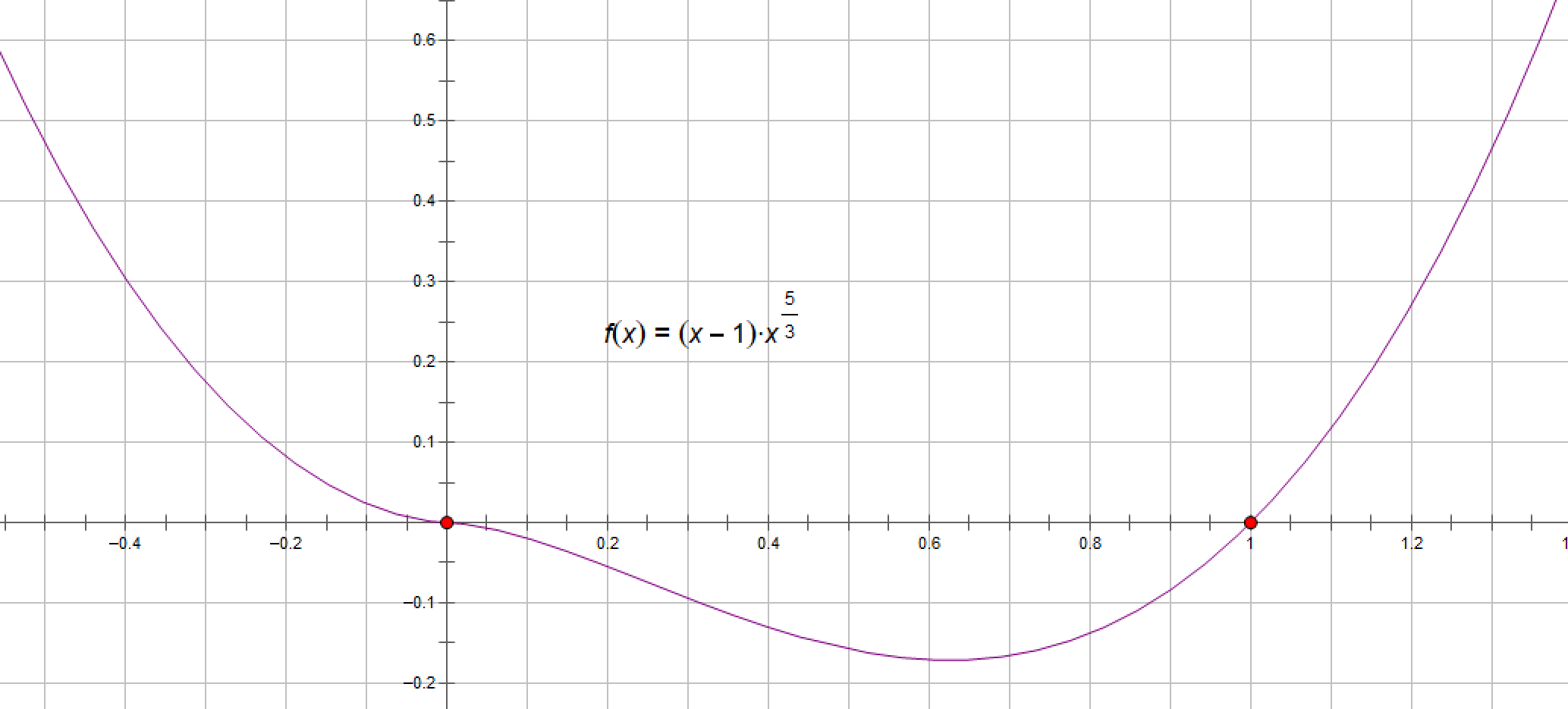
由此可得,曲线y=(x-1)x^5/3的下凸区间为(-∞,0)和(1/4,+∞),上凸区间为 (0.1/4),拐点为(0,0)和(1/4,-3/(32*2^1/3))

利用函数曲线的凸性可证明一些不等式.

例1：证明: e^(x+y)/2 <1/2(e^x+e^y),x,y∈(-∞,+∞).

观察不等式,可取函数 y= e^x.因 y''=e^x>0(x∈(-∞,+∞)),故曲线y=e^x在(-∞,+∞)上是下凸的,因此对于任何 x≠y,有f((x+y)/2)<1/2(f(x)+f(y)),即e^(x+y)/2 <1/2(e^x+e^y)

曲线的渐近线

如果当曲线伸向无穷远处时,它能渐渐靠近一条直线,那么就可以对曲线在无穷远部分的趋势有所了解,这条直线就是曲线的渐近线,如双曲线就有两条渐近线.

定义4.5.3若曲线C上的动点P沿曲线无限地远离原点时,点P与某一条直线L的距离趋于零,则称直线L为曲线C的渐近线

渐近线有三种:竖直渐近线、水平渐近线和斜渐近线

1. 竖直渐近线

若x→x₀+,lim f(x)=∞(或x→x₀-,lim f(x)=∞）,则当x→x₀+(或x→x₀-)时,曲线上的点 P(x,f(x))无限远离原点,且与直线x=x₀的距离趋于零,因此,直线x=x₀ 是曲线y=f(x)的一条渐近线,这样的渐近线称为y=f(x)的竖直渐近线.

例如,对于函数y=1/(x-1),x→1有lim1/(x-1)=∞,因此,直线x=1是曲线y=1/(x-1)的一条竖直渐近线.

2.水平渐近线

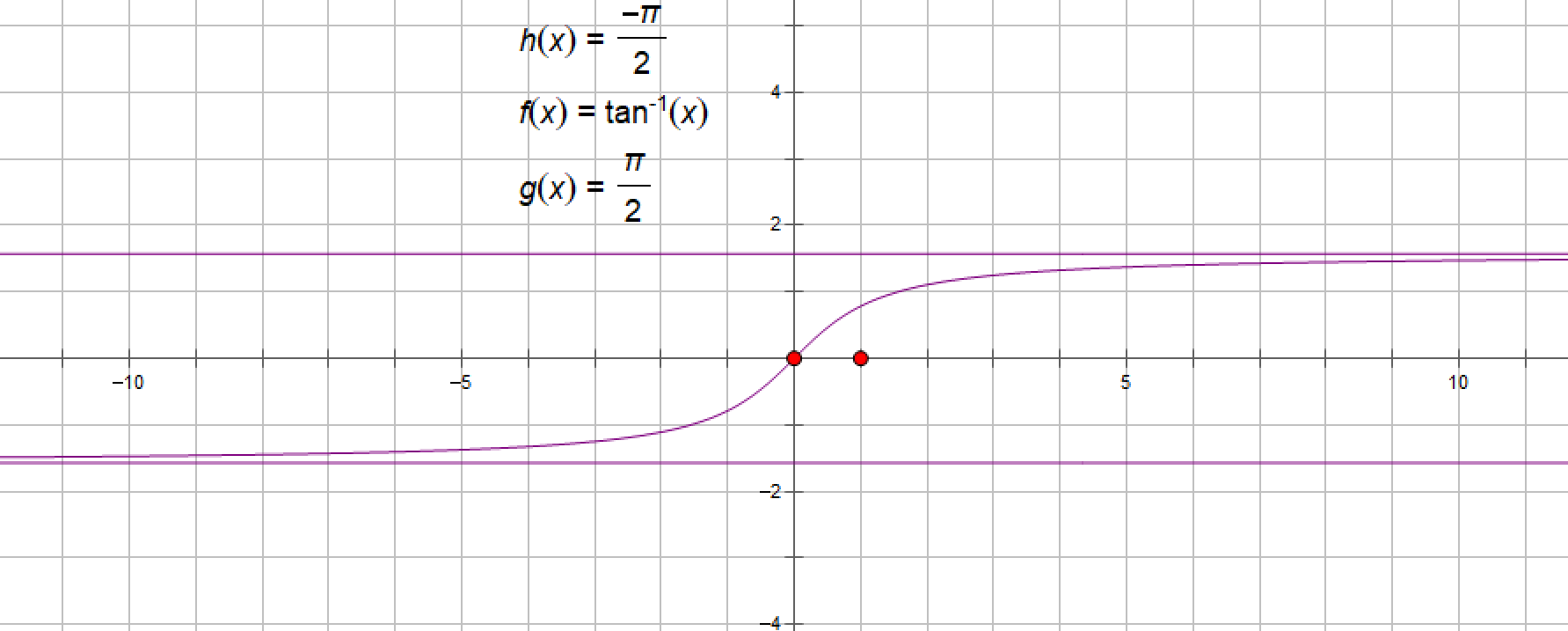
若x→+∞,lim f(x)=b(或x→-∞,lim f(x)=b）,则当x→+∞(或x→-∞)时,曲线上的点 P(x,f(x))无限远离原点,且与直线y=b的距离趋于零.因此,直线y=b是曲线y=f(x)的一条渐近线.这样的渐近线称为y=f(x)的水平渐近线.

例如,对于函数y=arctanx,有x→+∞,lim arctanx=π/2，x→-∞,lim arctanx=-π/2，因此,直线 y=-π/2和y=π/2是曲线y=arctanx的两条水平渐近线

3. 斜渐近线

若曲线y=f(x)当x→+∞ 时有斜渐近线y=ax+b(a≠0),则曲线上点P(x,f(x))到直线y=ax+b的距离为|f(x)-ax -b|/√(1+a²)     (4.5.2)

按定义,有x→+∞,lim|f(x)-ax -b|/√(1+a²) = 0 ,或x→+∞，lim[f(x)-ax]=b    (4.5.3)

又因为x→+∞, lim[f(x)/x-a]= lim 1/x*[f(x)-ax]=0·b=0,得x→+∞, limf(x)/x=a  (4.5.4)

于是,斜渐近线y=ax+b的系数a和b可由上面两式相继确定。反之,若由(4.5.4)、(4.5.3)两式求得a和b,则显然(4.5.2)式成立.因此曲线y≡f(x)当→+∞ 时有渐近线 y=ax +b.

曲线当x→-∞时的斜渐近线也有类似的结果.

例1：求曲线y=x+arctanx 的渐近线.

 

因为x→∞,lim f(x)/x=lim(1+1/x*arctanx)=1+0=1,故a=1,而f(x)-ax=x+arctanx-x=arctanx,x→+∞, lim arctanx=π/2,得b1=π/2,由x→-∞,  lim arctanx =-π/2得，b2=-π/2，

因此,曲线y=x+arctanr有两条斜渐近线,它们分别是:当π→ +∞ 时的斜渐近线为 y=x+π/2,当x→-∞ 时的斜渐近线为 y=x-π/2

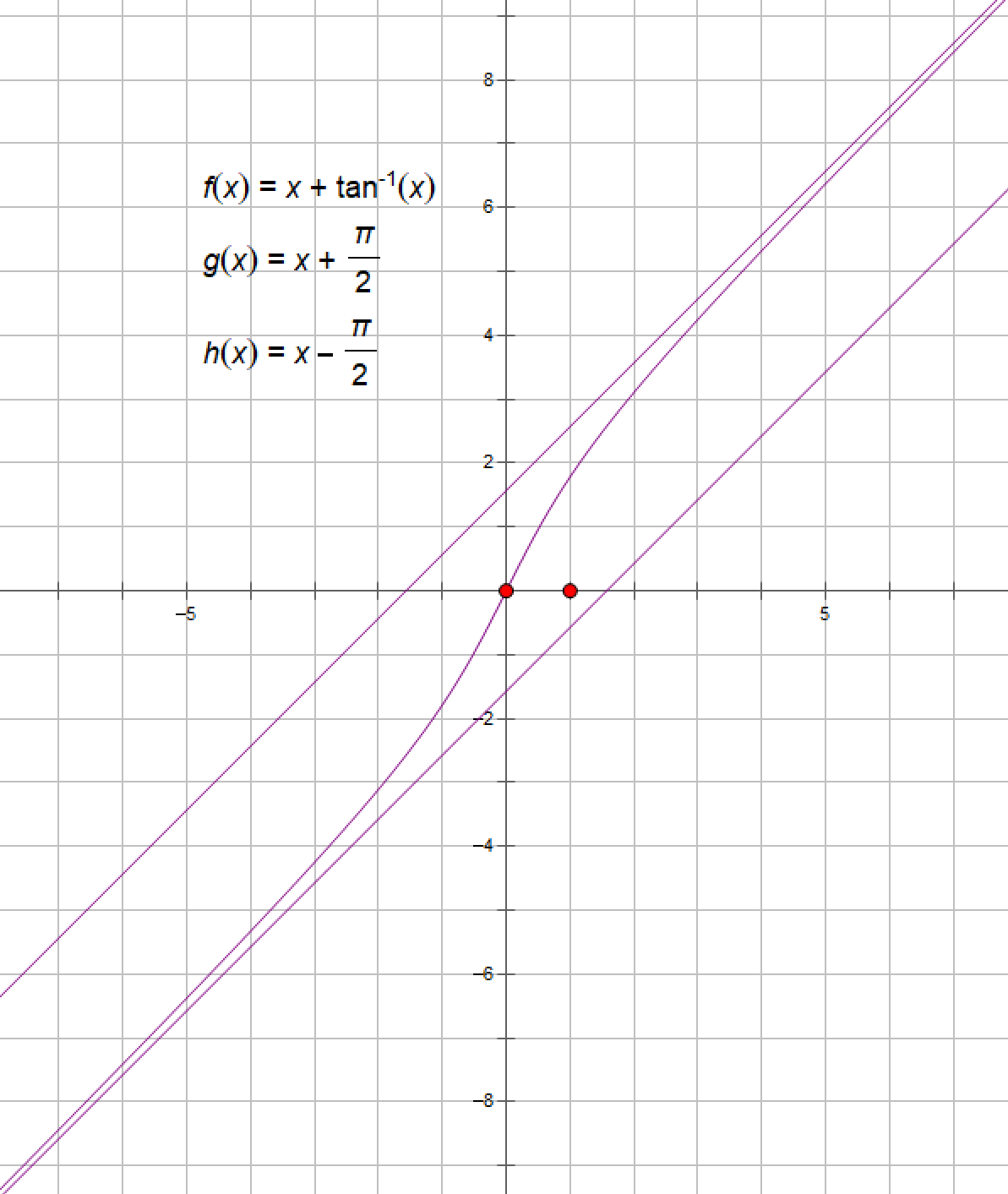
注 函数曲线的水平渐近线与斜渐近线之和最多为两条，而竖直渐近线则可以有多条.

函数图形的描绘

利用函数的一阶导数,可以确定函数图形的单调区间.利用函数的二阶导数,可以确定函数图形的上、下凸区间和拐点.利用渐近线,可使我们对函数图形无限远部分的趋势有所了解,这样就可较准确地描绘出函数的图形.描绘函数图形的步骤如下:

(1)确定函数的定义域;

(2)考察函数的奇偶性、周期性;

(3)求出函数的一阶导数及导数为零和不存在的点,

求出函数的二阶导数及二阶导数为零和不存在的点,

求出函数的不连续点;

(4)用第三步得到的点,按照从小到大的次序,将定义域分成若午个小区间,列表讨论在每个小区间上的一阶和二阶导数的符号,以确定函数在各个小区间上的单调性、凸性及极值点、拐点;

(5)求出曲线的渐近线;

(6)求出曲线某些特殊点的坐标,如与两坐标轴的交点、不连续点、不可导点等,如果需要,还可以再加入几个点;

(7)根据以上结果描绘出函数的图形.

 

例1:作函数f(x)=x/(1+x²)的图形.

(1)函数的定义域为(-∞,+∞);

(2)该函数为奇函数,因此只需讨论它在[0,+∞)上的图形,

(3) 一阶导数f'(x)=(1-x²)/(1+x²)²,一阶导数为0的点x=1,x=-1,

二阶导数f"(x)=2x(x²-3)(1+x²)^{-3,二阶导数为0的点x=0,x=√3,x=-√3}

(4)根据一阶导数为0的点和不存在的点，二接导数为0的点和不存在的点,如表 4.5 所示;

(5)由x→∞时，limf(x)=0知曲线有水平渐近线y=0.

根据上面的讨论,描出函数在(0,+∞)上的图形;再由曲线关于原点的对称性,得到函数在(-∞,0)上的图形

7、曲率

一般来说,一条曲线在不同部分有不同的弯曲程度,直观看来,抛物线y=x²在其顶点附近弯曲得比远离顶点的部分要大些.

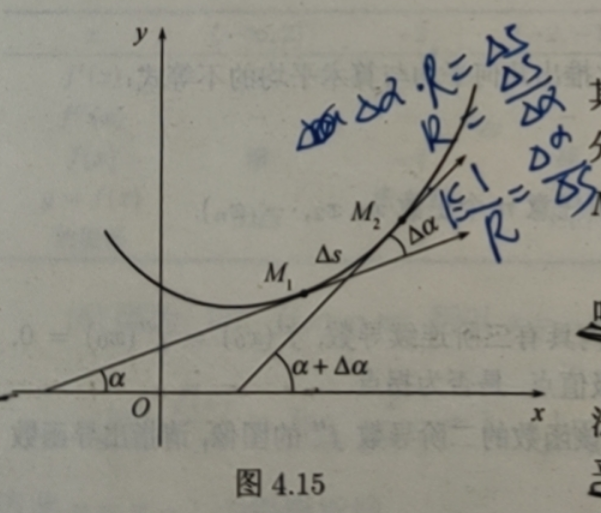
如图4.15,设M1M2为曲线上的弧段其长度为|Δs|,点M1,M2处切线的倾角分别为 α,α+Δα,那么当动点从M1移动到M2时切线转过的角度为|Δα|,比值|Δα|/|Δs|叫弧段 M1M2的平均曲率.

类似于从平均速度引进瞬时速度的方法,当Δs→0时 (即 M1→ M2 时),上述平均曲率的极限如果存在，则称此极限为曲线C 在点 M1处的曲率,记作K,即

 对于直线来说，切线与直线本身重合,当点沿直线移动时,切线倾角α不变，Δα≡0，故K= 0.这就是说直线上任意点处的曲率都为零。

 对于圆来说,如果它的光径为R,则有Δs = RΔα.故Δs→0时，lim|Δα|/|Δs|=lim|Δα|/|ΔαR|=1/R

 这就是说圆上任意点处的曲率都是半径的倒数,因此将曲率的倒数称为曲率半径.

在一般情况下,设曲线y=f(x),且f(x)具有二阶导数,曲线上M1与 M2对应于x轴上的坐标分别为x与x+Δx,则

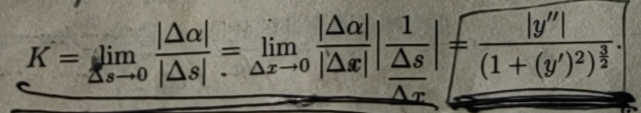
 这就是计算曲率的公式.

例1：抛物线y=ax²+bx+c上哪一点处曲率最大?

由y=ax²+bx+c可得y=2ax+b,y"=2a,因此K=|2a|/[1+(2a+b)²]^3/2 
显然,当 2ax+b≡0,即x=-b/2a时，K最大。而x=-b/2a处所对应的点为抛物线的顶点.因此,抛物线在顶点处的曲率最大.

对于由参数方程给出的函数

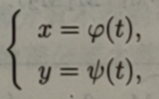
则可利用由参数方程所确定的函数的求导法,求出y'_x及y”_x,代入(4.6.3)式便得

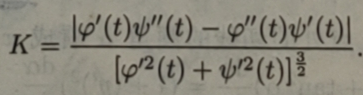
这是计算由参数方程给出的函数的曲率的公式.

因曲率的倒数为曲率半径,因此曲率半径的计算公式为

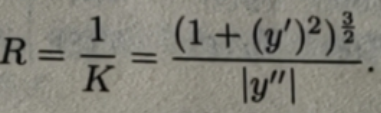
由此可见,若曲线上某点处曲率半径较大,则曲线在该点处的曲率较小,因而曲线在该点的弯曲程度就较小.

在曲线L上的点M处沿曲线凹向一侧的法线上截取线段MN=R,点N称为该曲线上点M处的曲率中心,以N为圆心,曲率半径R为半径的圆,叫该曲线在该点M处的曲率圆.由曲率圆的定义可知，在点M处曲线和曲率圆有相同的曲率K,即这二者的弯曲程度相同.因此,在研究曲线上某点附近的弧段时,可以用该点处曲率圆上相应的圆弧近似地代替,从而以圆的知识来分析曲线上这一弧段的情况

六、四种深度学习常见激活函数

激活函数

在计算机网络中，一个节点的激活函数定义了该节点在给定的输入或输入的集合下的输出。标准的计算机芯片电路可以看作是根据输入得到开（1）或关（0）输出的数字电路激活函数。这与神经网络中的线性感知机的行为类似。然而，只有非线性激活函数才允许这种网络仅使用少量节点来计算非平凡问题。 在人工神经网络中，这个功能也被称为传递函数。

sigmoid函数和tanh函数是研究早期被广泛使用的2种激活函数。两者都为S 型饱和函数。 当sigmoid 函数输入的值趋于正无穷或负无穷时，梯度会趋近零，从而发生梯度弥散现象。sigmoid函数的输出恒为正值，不是以零为中心的，这会导致权值更新时只能朝一个方向更新，从而影响收敛速度。tanh 激活函数是sigmoid 函数的改进版，是以零为中心的对称函数，收敛速度快，不容易出现 loss 值晃动，但是无法解决梯度弥散的问题。2个函数的计算量都是指数级的，计算相对复杂。softsign 函数是 tanh 函数的改进版，为 S 型饱和函数，以零为中心，值域为（−1，1）。

sigmoid函数

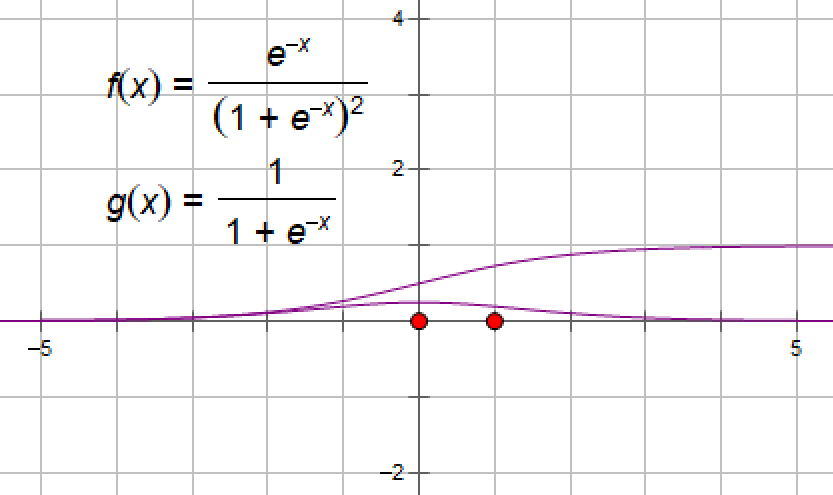
在信息科学中，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间。

（1）、函数公式：sig(x)=1/(1+e^-x)

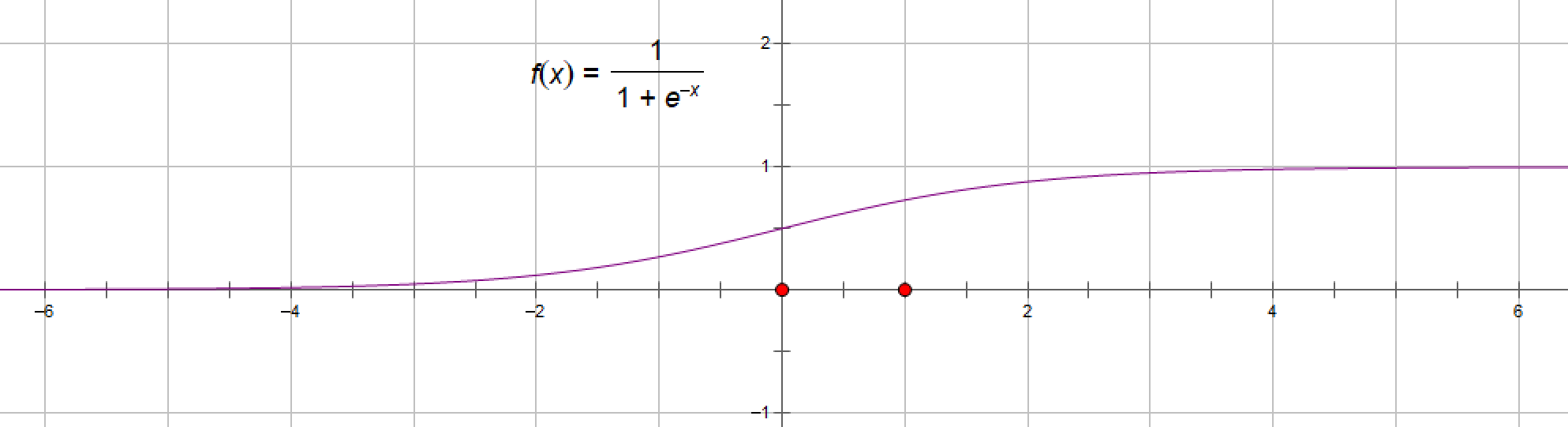
当x=0时，y=0.5.

渐近线：

若x→+∞,lim 1/(1+e^-x)=1,x→-∞,lim 1/(1+e^-x)=0,故y=1和y=0是该函数的渐近线。

该饱和函数的上、下界为（0,1）

（2）、导函数

其对x的导数可以用自身表示：s'(x)=e^-x/(1+e^-x)² =s(x)(1-s(x))

导函数图像为：

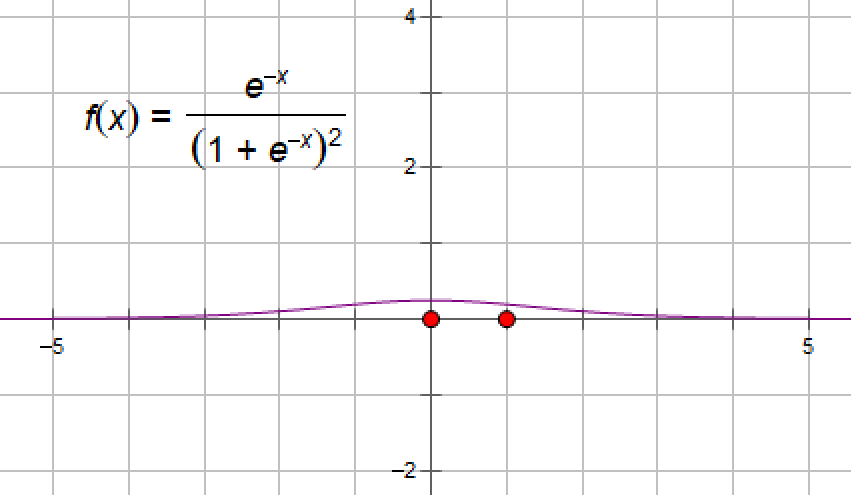
当x=0时，y=0.25.即导函数最大值为0.25.

将sigmoid函数及其导数画在同一个图中如下所示：

（3）、sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid函数为神经网络中的激励函数，是一种光滑且严格单调的饱和函数，其表达式为：

（4）、具有以下优缺点：

优点：平滑、易于求导。

Sigmoid函数将输出映射在(0,1)之间，单调连续，单调递增，反函数单调递增。

输出范围有限，优化稳定，可以用作输出层。

在特征相差比较复杂或者相差不是特别大的时候效果比较好,

缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；

反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。(由于其软饱和性，容易产生梯度消失，导致训练出现问题。)

（5）、软饱和性

导函数：s'(x)=e^-x/(1+e^-x)²

可见，sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0，即:

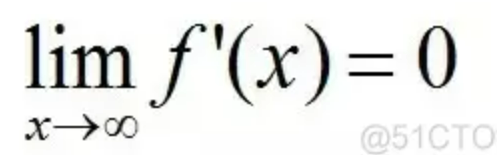
Bengio 教授等将具有这类性质的激活函数定义为软饱和激活函数。与极限的定义类似，饱和也分为左侧软饱和与右侧软饱和:

左侧软饱和：

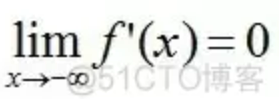
 右侧软饱和：

 

与软饱和相对的是硬饱和激活函数，即:f‘(x)=0，当|x| >c，其中c为常数。同理，硬饱和也分为左侧硬饱和和右侧硬饱和。常见的ReLU 就是一类左侧硬饱和激活函数。

软饱和性的劣势: 

Sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid向下传导的梯度包含了一个f'(x)因子(sigmod关于输入的导数)，因此一旦输入落入饱和区，f'(x)就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在5 层之内就会立牛梯度消失现象[Understandina the dificulty of trainina deep feedforward neural networksl、梯度消失问题至今仍然存在，但被新的优化方法有效缓解了，例如DBN中的分层预训练，Batch Normalization的逐层归一化，Xavier和MSRA权重初始化等代表性技术,

软饱和性的优势: Sigmoid 的饱和性虽然会导致梯度消失，但也有其有利的一面。例如它在物理意义上最为接近生物神经元。(0.1)的输出还可以被表示作概率，或用于输入的归一化，代表性的如Sigmoid交叉熵损失函数。

（6）、梯度消失

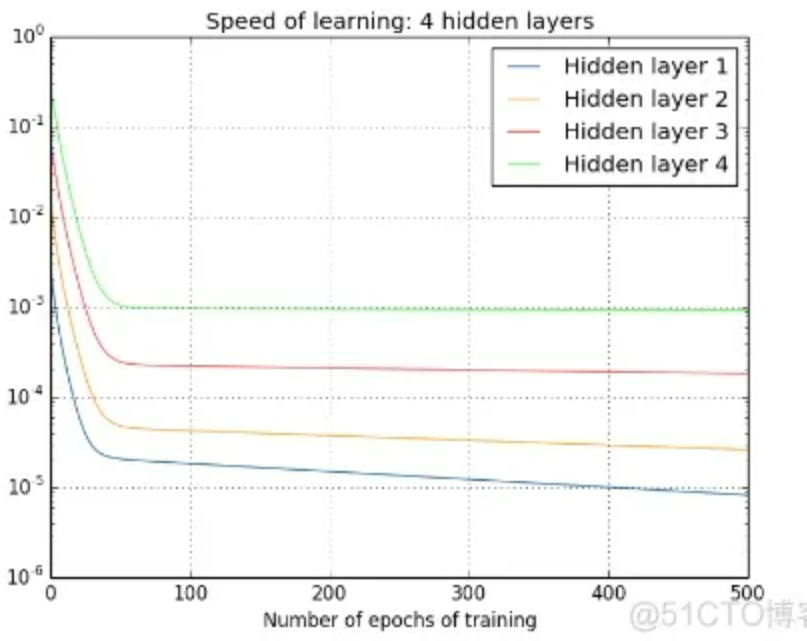
当使用sigmoid作为激活函数时，随着神经网络隐含层(hidden layer)层数的增加，训练误差反而加大。表现为:
靠近输出层的隐含层梯度较大，参数更新速度快，很快就会收敛;

靠近输入层的隐含层梯度较小，参数更新速度慢，几乎和初始状态一样，随机分布;

在含有四个隐藏层的网络结构中，第一层比第四层慢了接近100倍!

这种现象就是梯度弥散(vanishing gradient)或称梯度消失。

而另一种情况，梯度爆炸(exploding gradient)，则是前面层的梯度，通过训练变大，导致后面层的梯度，以指数级增大。

sigmoid的更新速率图：

 

 

tanh双曲正切函数

（1）、函数表达式：tanh(x)=(ex - e-x) / (ex + e-x)

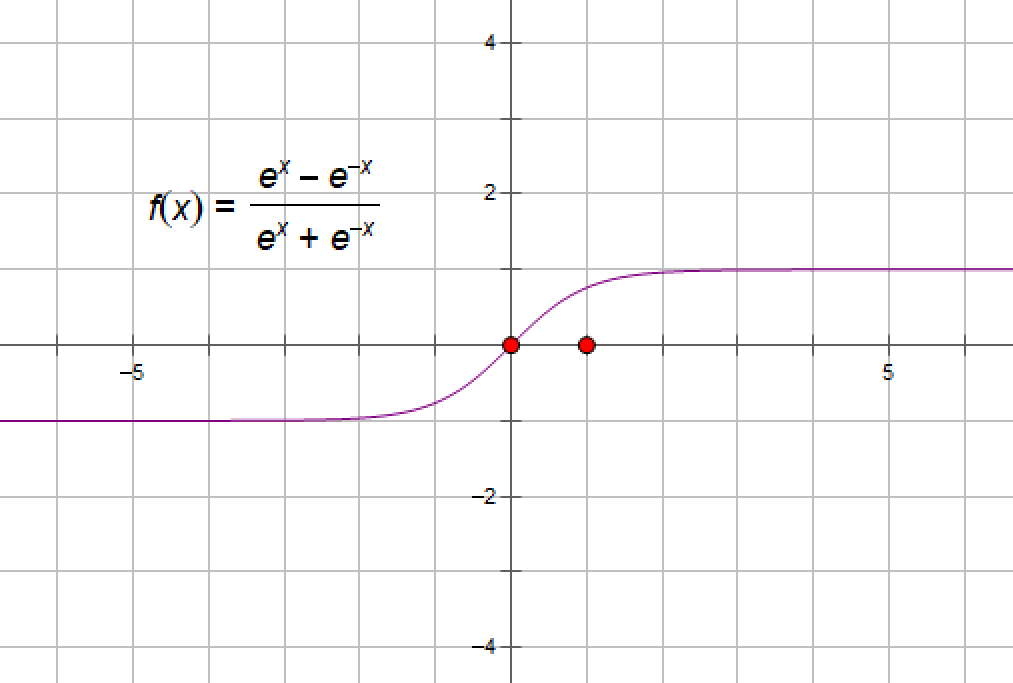
（2）、导函数：tanh'(x)=4e^2x/(e^2x+1)² 

 

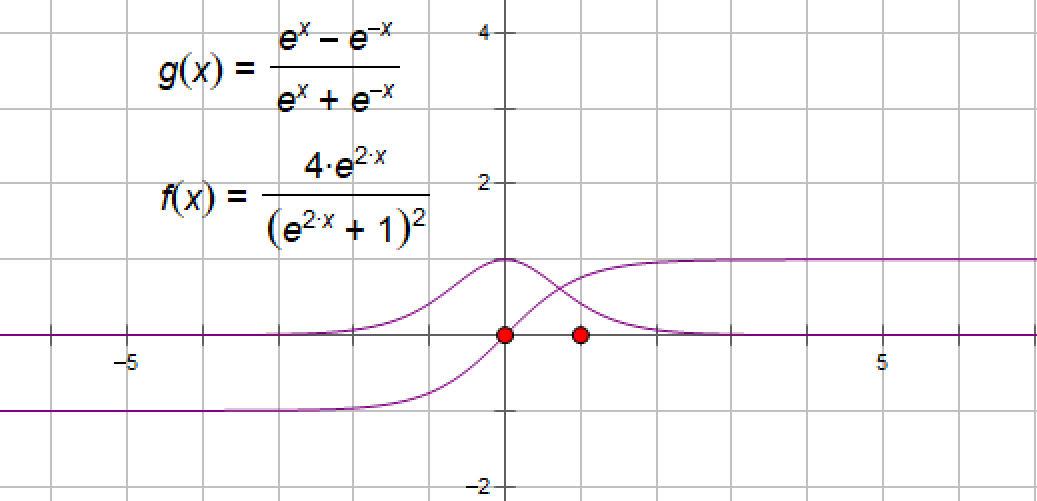
当x=0时，y=1,即导函数最大值为1.

（3）、优缺点

缺点：tanh和sigmoid一样具有饱和性，会造成梯度消失。

优点：

tanh，即双曲正切(hyperbolic tangent)，类似于幅度增大sigmoid，将输入值转换为-1至1之间。

tanh的导数取值范围在0至1之间，优于sigmoid的0至1/4，在一定程度上，减轻了梯度消失的问题。

tanh的输出和输入能够保持非线性单调上升和下降关系，符合BP(back propagation)网络的梯度求解，容错性好，有界。
与sigmoid相比，tanh的输出均值为0，这使得它的收敛速度要比sigmoid快，减少了迭代更新的次数。

（4）、sigmoid和tanh:

sigmoid在输入处于[-1,1]之间时，函数值变化敏感，一旦接近或者超出区间就失去敏感性，处于饱和状态，影响神经网络预测的精度值;

tanh的变化敏感区间较宽，导数值渐进于0、1，符合人脑神经饱和的规律，比sigmoid函数延迟了饱和期;

tanh在原点附近与y=x函数形式相近，当激活值较低时，可以直接进行矩阵运算，训练相对容易;

 tanh和sigmoid都是全部激活(fire)，使得神经网络较重(heavy)。

softsign软符号函数

 （1）、函数公式：f(x)=x/(1+|x|)

 图像如下：

（2）、导函数

softsign函数的导函数是

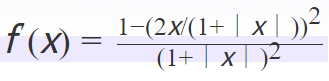
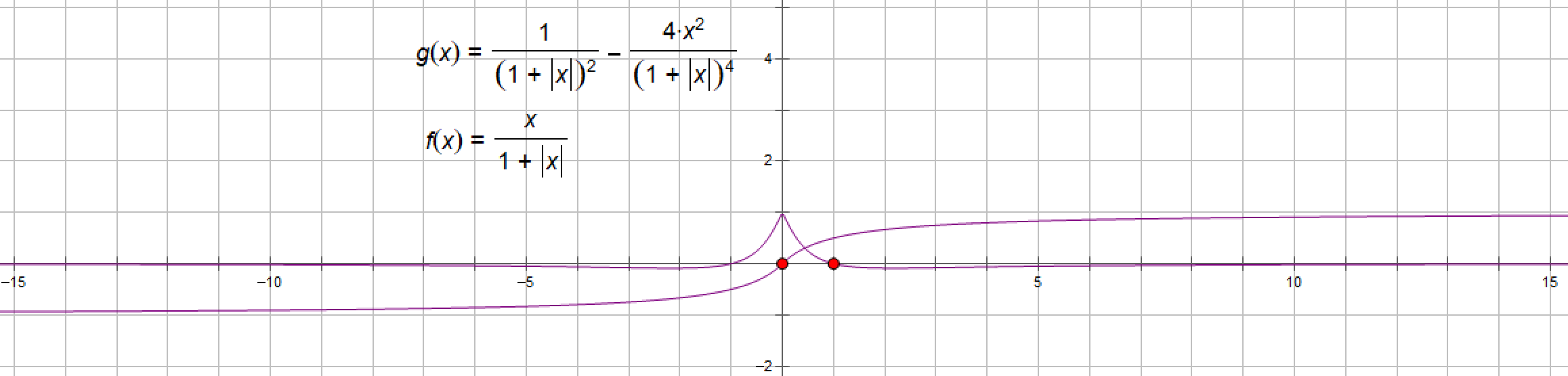
 软符号函数(Softsign function)是一种常用的激活函数，用于神经网络中的神经元激活。它在数学上是一个光滑的非线性函数，可以将输入的实数映射到一个介于-1和1之间的输出范围内。

软符号函数的主要特点是它在接近于正无穷和负无穷时都趋于饱和状态，即输出值逐渐接近1和-1。而在接近于0的位置，函数的斜率较大对输入的微小变化非常敏感。因此，软符号函数在处理较大数值时可以避免梯度爆炸的问题，并且在处理小数值时具有较高的灵敏度。

 与其他常用的激活函数相比，软符号函数具有以下几个优势

 1.避免梯度爆炸:在神经网络中，梯度爆炸是一个常见的问题，它会导致训练过程中的权重更新过大，从而影响网络的收敛速度和性能。软符号函数的饱和性质可以有效地避免梯度爆炸的问题，使得网络的训练更加稳定。

2.改善稀疏性:在某些情况下，神经网络的输出需要被限制在一个特定的范围内，以避免结果过大或过小。软符号函数在接近于正无穷和负无穷时趋近于1和-1，从而可以有效地改善网络的稀疏性，使得输出值在一个合理的范围内。

 3.增强敏感度:软符号函数在接近于0的位置具有较高的斜率，对输入的微小变化非常敏感。这使得软符号函数在处理小数值时具有较高的灵敏度，能够更好地捕捉输入数据的细微变化，提高神经网络的表达能力。

 尽管软符号函数在某些特定场景下具有一定的优势，但它也存在一些限制和不足之处:

1.饱和性:软符号函数在接近于正无穷和负无穷时趋于饱和状态，导致输出值无法超过1和-1。这可能会限制网络的表达能力，特别是在处理需要较大输出范围的任务时，

2.零点限制:软符号函数在输入为0时的输出也为0，这可能会导致网络在处理输入为0的情况下失去灵敏度，降低了网络对输入数据的响应能力。

总的来说，软符号函数作为一种常用的激活函数，具有一定的优势和不足之处。在实际应用中，我们需要根据具体的任务需求和数据特点选择合适的激活函数，以提高神经网络的性能和效果。

 

RELU函数

即Rectified Linear Unit，整流线性单元，激活部分神经元，增加稀疏性，当x小于0时，输出值为0，当x大于0时，输出值为x.

ReLU 是修正线性单元(rectified linear unit)，在 0 和 x 之间取最大值。

为什么要引入 ReLU？因为 sigmoid 和 tanh 容易导致梯度消失，而 ReLU 是非饱和激活函数，不容易发生梯度消失

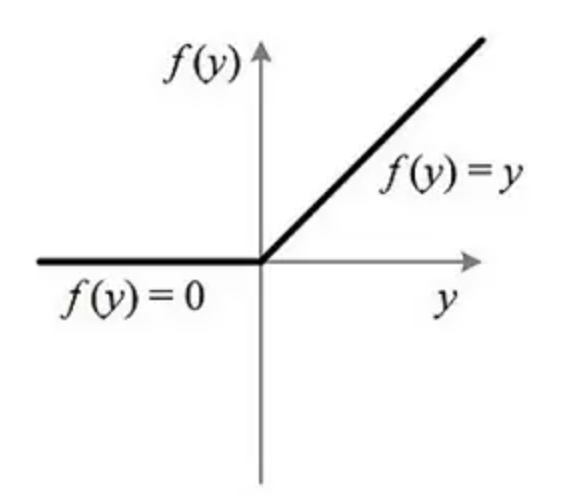
（1）、函数公式f(x)=max(0,x)

函数图像：

 

（2）、导函数 

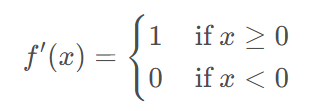
导函数图像：

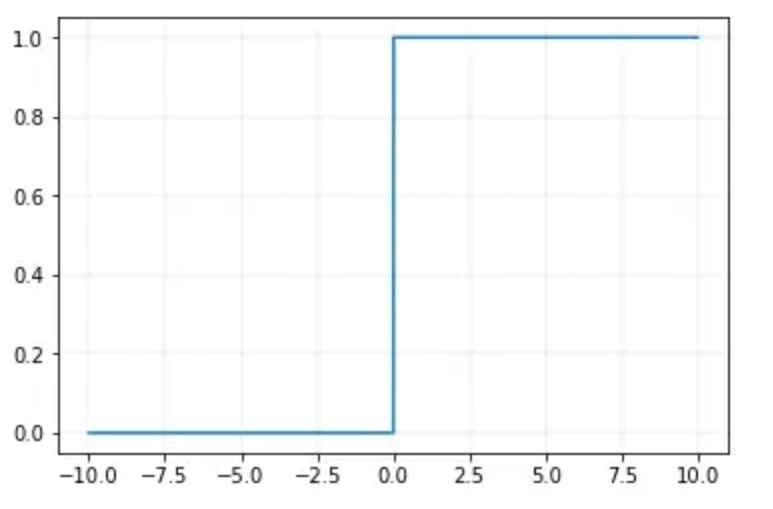
ReLU函数的导数为1或0，可以有效避免梯度消失问题。

 在深度学习中，ReLU层通常被用作激活函数，因为它可以有效地减少神经网络中的梯度消失问题

（3）、优缺点

优点：

① 有效缓解过拟合的问题，因为 ReLU 有可能使部分神经节点的输出变为 0，从而导致神经节点死亡，降低了神经网络的复杂度

②  不会发生梯度消失或梯度爆炸，当 x 大于 0 时，ReLU 的梯度恒为 1，不会随着网路深度的加深而使得梯度在累乘的时候变得越来越小或者越来越大，从而不会发生梯度消失或梯度爆炸

③ 计算简单，ReLU 本质上就是计算一次在两个值中取最大值

缺点：

① 会导致神经元死亡，当一个神经元在某次的激活值为 0 之后，此后得到的激活值都是 0.