深度神经网络(DNN,Deep Neural Network)
神经网络不应该看做是一个算法,应该看做是一个特征挖掘方法。在实际的业界发展过程中,数据的作用往往大于模型,当我们把数据的隐藏特征提取出来之后,用很简单的模型也能预测的很好。
神经网络模型由生物神经中得到启发。在生物神经元细胞中,神经突触接收到信号,经过接收并处理信号后判断信号的信息强弱,来做出不同神经电位变化反应。受此启发,科研人员设计出基础的神经网络模型结构,神经元模型(Neuron Model)。
一、从感知机到神经网络
1.1 感知机
下图为一个最简单的“M-P神经元结构”,该模型1943年提出,并一直沿用至今:
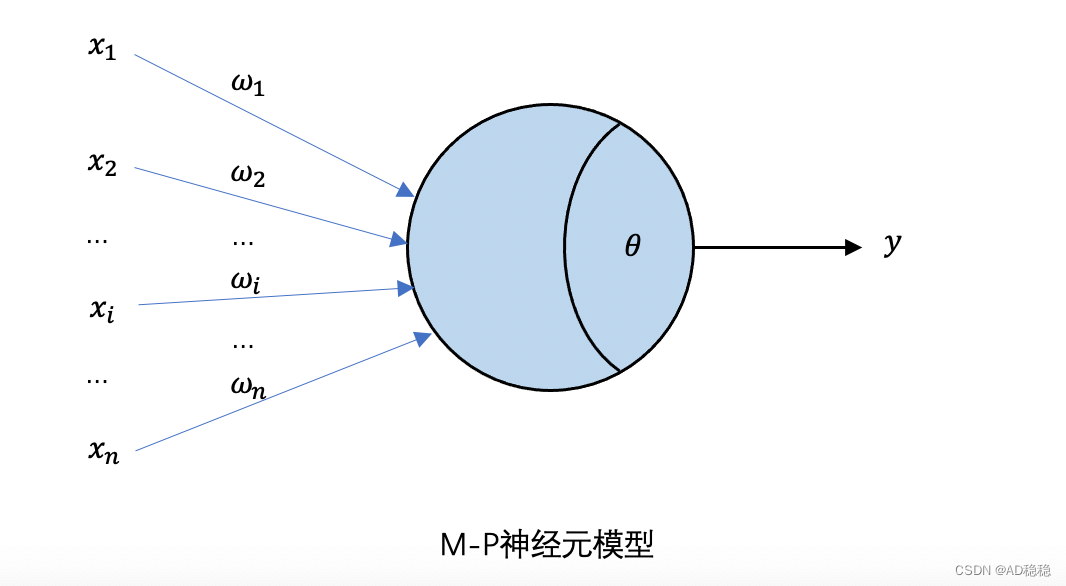
从模型示意图看,对于一个单一的神经元模型,其中{x1,x2,......,xn}为该模型的输入数据;{ω1,ω2,......,ωn}为神经元模型计算参数,与输入数据维度一一对应,用于反应输入数据各维度的权重;θ表示神经元输出阈值,通常用于控制神经元是否输出结果或修正输出结果;为神经元模型的输出结果,计算方式如下公式:
其中,函数f 用于将函数值映射至区间[0, 1](主要)或[-1, 1](部分),函数 f 通常称为激活函数(activation function)。常用的激活函数包括Sigmoid、Tanh函数等。
单层感知机能够经过简单地 学习实现输入值得“与”、“或”和“非”运算,但是单层感知机只能实现线性可分的数据学习(存在一个超平面使得数据分开),当线性不可分时单层感知机便无法处理。如“异或”操作,单层感知机即无法实现。
为了能够使得感知机的适应范围更广,可以将多个感知机进行连接,构成多层感知机模型来适应更复杂的任务。多层感知机模型也被称作人工神经网络(Artificial Neuron Network,ANN),将在下一篇进行介绍。
1.2 神经网络
1)为了增强模型的表达能力,在神经网络中加入了隐藏层,隐藏层可以有多层,如下图实例,当然增加了这么多隐藏层模型的复杂度也增加了好多。
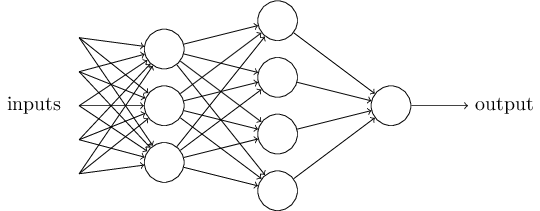
2)输出层的神经元也可以不止一个输出,可以有多个输出,这样模型可以灵活的应用于分类回归,以及其他的机器学习领域比如降维和聚类等。多个神经元输出的输出层对应的一个实例如下图,输出层现在有4个神经元了。
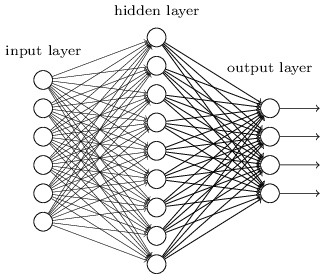
3)对激活函数做扩展,感知机的激活函数是 sign(z),虽然简单但是处理能力有限,因此神经网络中一般使用的其他的激活函数,比如我们在逻辑回归里面使用过的Sigmoid函数,即:
还有后来出现的tanx, softmax,和ReLU等。通过使用不同的激活函数,神经网络的表达能力进一步增强。
2. DNN的基本结构
DNN可以理解为有很多隐藏层的神经网络。这个很多其实也没有什么度量标准, 多层神经网络和深度神经网络DNN其实也是指的一个东西,当然,DNN有时也叫做多层感知机(Multi-Layer perceptron,MLP), 名字实在是多。后面我们讲到的神经网络都默认为DNN。
从DNN按不同层的位置划分,DNN内部的神经网络层可以分为三类,输入层,隐藏层和输出层,如下图示例,一般来说第一层是输入层,最后一层是输出层,而中间的层数都是隐藏层。
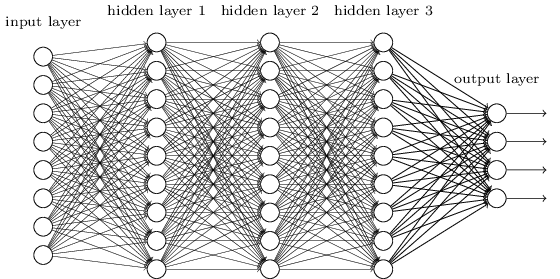
层与层之间是全连接的,也就是说,第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂,但是从小的局部模型来说,还是和感知机一样,即一个线性关系 Z=∑wixi+b 加上一个激活函数sigma(z)。
由于DNN层数多,则我们的线性关系系数 w 和偏置 b 的数量也就是很多了。具体的参数在DNN是如何定义的呢?
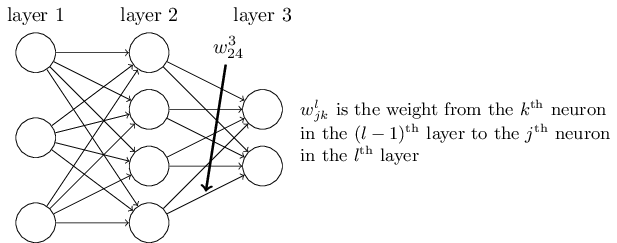
首先我们来看看线性关系系数 w 的定义。以下图一个三层的DNN为例,第二层的第4个神经元到第三层的第2个神经元的线性系数定义为 w324。上标3代表线性系数 w 所在的层数,而下标对应的是输出的第三层索引2和输入的第二层索引4。
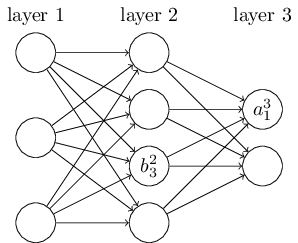
再来看看偏置 b 的定义。还是以这个三层的DNN为例,第二层的第三个神经元对应的偏置定义为 b23。其中,上标2代表所在的层数,下标3代表偏倚所在的神经元的索引。同样的道理,第三个的第一个神经元的偏置应该表示为 b31。同样的,输入层是没有偏置参数 b 的。
3. DNN前向传播算法数学原理
在上一节,我们已经介绍了DNN各层线性关系系数 w,偏置 b的定义。假设我们选择的激活函数是<span id="MathJax-Span-209" class="mrow"><span id="MathJax-Span-210" class="mi">&sigma;(z),隐藏层和输出层的输出值为 a,则对于下图的三层DNN,利用和感知机一样的思路,我们可以利用上一层的输出计算下一层的输出,也就是所谓的DNN前向传播算法。
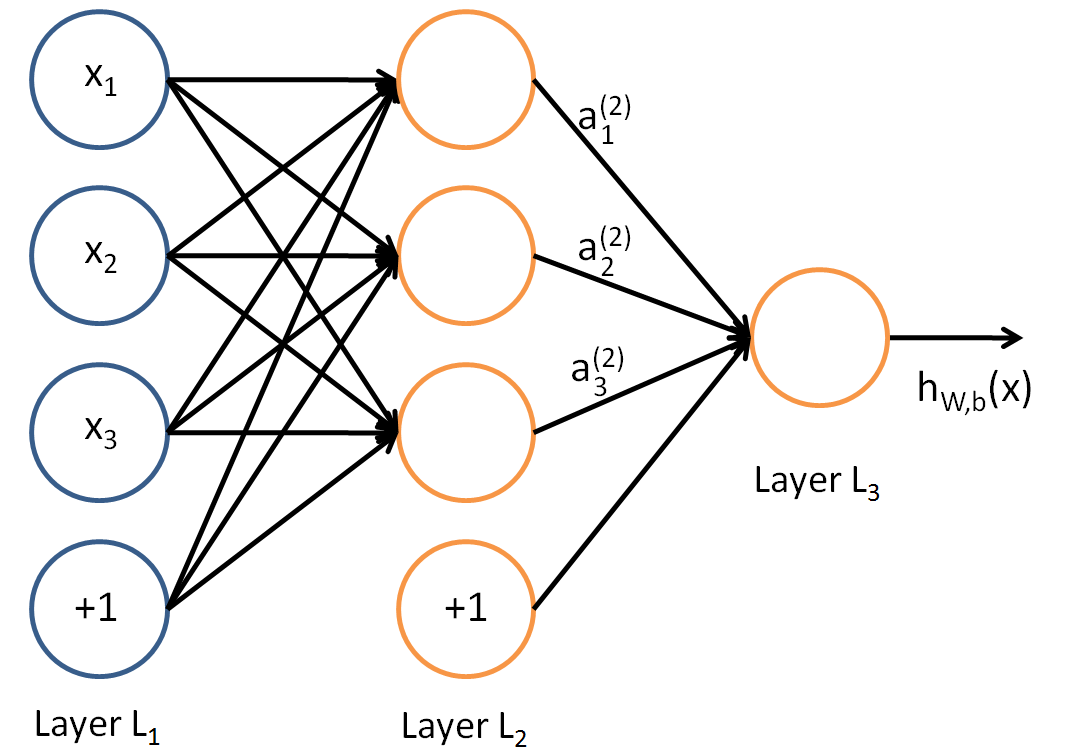
对于第二层的的输出<span id="MathJax-Span-218" class="mrow"><span id="MathJax-Span-219" class="msubsup"><span id="MathJax-Span-220" class="mi">a21,a22,a23a12,a22,a32,我们有:
对于第三层的的输出<span id="MathJax-Span-396" class="mrow"><span id="MathJax-Span-397" class="msubsup"><span id="MathJax-Span-398" class="mi">a31a13,我们有:
将上面的例子一般化,假设第<span id="MathJax-Span-459" class="mrow"><span id="MathJax-Span-460" class="mi">l−1l−1层共有m个神经元,则对于第<span id="MathJax-Span-464" class="mrow"><span id="MathJax-Span-465" class="mi">ll层的第j个神经元的输出<span id="MathJax-Span-467" class="mrow"><span id="MathJax-Span-468" class="msubsup"><span id="MathJax-Span-469" class="mi">aljajl,我们有:
其中,如果<span id="MathJax-Span-519" class="mrow"><span id="MathJax-Span-520" class="mi">l=2l=2,则对于的<span id="MathJax-Span-524" class="mrow"><span id="MathJax-Span-525" class="msubsup"><span id="MathJax-Span-526" class="mi">a1kak1即为输入层的<span id="MathJax-Span-530" class="mrow"><span id="MathJax-Span-531" class="msubsup"><span id="MathJax-Span-532" class="mi">xkxk。
从上面可以看出,使用代数法一个个的表示输出比较复杂,而如果使用矩阵法则比较的简洁。假设第<span id="MathJax-Span-535" class="mrow"><span id="MathJax-Span-536" class="mi">l−1l−1层共有m个神经元,而第<span id="MathJax-Span-540" class="mrow"><span id="MathJax-Span-541" class="mi">ll层共有n个神经元,则第<span id="MathJax-Span-543" class="mrow"><span id="MathJax-Span-544" class="mi">ll层的线性系数<span id="MathJax-Span-546" class="mrow"><span id="MathJax-Span-547" class="mi">ww组成了一个<span id="MathJax-Span-549" class="mrow"><span id="MathJax-Span-550" class="mi">n×mn×m的矩阵<span id="MathJax-Span-554" class="mrow"><span id="MathJax-Span-555" class="msubsup"><span id="MathJax-Span-556" class="mi">WlWl, 第<span id="MathJax-Span-559" class="mrow"><span id="MathJax-Span-560" class="mi">ll层的偏倚<span id="MathJax-Span-562" class="mrow"><span id="MathJax-Span-563" class="mi">bb组成了一个<span id="MathJax-Span-565" class="mrow"><span id="MathJax-Span-566" class="mi">n×1n×1的向量<span id="MathJax-Span-570" class="mrow"><span id="MathJax-Span-571" class="msubsup"><span id="MathJax-Span-572" class="mi">blbl , 第<span id="MathJax-Span-575" class="mrow"><span id="MathJax-Span-576" class="mi">l−1l−1层的的输出<span id="MathJax-Span-580" class="mrow"><span id="MathJax-Span-581" class="mi">aa组成了一个<span id="MathJax-Span-583" class="mrow"><span id="MathJax-Span-584" class="mi">m×1m×1的向量<span id="MathJax-Span-588" class="mrow"><span id="MathJax-Span-589" class="msubsup"><span id="MathJax-Span-590" class="mi">al−1al−1,第<span id="MathJax-Span-597" class="mrow"><span id="MathJax-Span-598" class="mi">ll层的的未激活前线性输出<span id="MathJax-Span-600" class="mrow"><span id="MathJax-Span-601" class="mi">zz组成了一个<span id="MathJax-Span-603" class="mrow"><span id="MathJax-Span-604" class="mi">n×1n×1的向量<span id="MathJax-Span-608" class="mrow"><span id="MathJax-Span-609" class="msubsup"><span id="MathJax-Span-610" class="mi">zlzl, 第<span id="MathJax-Span-615" class="mrow"><span id="MathJax-Span-616" class="mi">ll层的的输出<span id="MathJax-Span-618" class="mrow"><span id="MathJax-Span-619" class="mi">aa组成了一个<span id="MathJax-Span-621" class="mrow"><span id="MathJax-Span-622" class="mi">n×1n×1的向量<span id="MathJax-Span-626" class="mrow"><span id="MathJax-Span-627" class="msubsup"><span id="MathJax-Span-628" class="mi">alal。则用矩阵法表示,第l层的输出为:
这个表示方法简洁漂亮,后面我们的讨论都会基于上面的这个矩阵法表示来。
4. DNN前向传播算法
有了上一节的数学推导,DNN的前向传播算法也就不难了。所谓的DNN的前向传播算法也就是利用我们的若干个权重系数矩阵<span id="MathJax-Span-663" class="mrow"><span id="MathJax-Span-664" class="mi">WW,偏倚向量<span id="MathJax-Span-666" class="mrow"><span id="MathJax-Span-667" class="mi">bb来和输入值向量<span id="MathJax-Span-669" class="mrow"><span id="MathJax-Span-670" class="mi">xx进行一系列线性运算和激活运算,从输入层开始,一层层的向后计算,一直到运算到输出层,得到输出结果为值。
输入: 总层数L,所有隐藏层和输出层对应的矩阵<span id="MathJax-Span-672" class="mrow"><span id="MathJax-Span-673" class="mi">WW,偏倚向量<span id="MathJax-Span-675" class="mrow"><span id="MathJax-Span-676" class="mi">bb,输入值向量<span id="MathJax-Span-678" class="mrow"><span id="MathJax-Span-679" class="mi">xx
输出:输出层的输出<span id="MathJax-Span-681" class="mrow"><span id="MathJax-Span-682" class="msubsup"><span id="MathJax-Span-683" class="mi">aLaL
1) 初始化<span id="MathJax-Span-686" class="mrow"><span id="MathJax-Span-687" class="msubsup"><span id="MathJax-Span-688" class="mi">a1=xa1=x
2) for <span id="MathJax-Span-693" class="mrow"><span id="MathJax-Span-694" class="mi">l=2l=2 to <span id="MathJax-Span-698" class="mrow"><span id="MathJax-Span-699" class="mi">LL, 计算:
最后的结果即为输出<span id="MathJax-Span-731" class="mrow"><span id="MathJax-Span-732" class="msubsup"><span id="MathJax-Span-733" class="mi">aLaL。
5. 反向传播
在了解DNN的反向传播算法前,我们先要知道DNN反向传播算法要解决的问题,也就是说,什么时候我们需要这个反向传播算法?
回到我们监督学习的一般问题,假设我们有m个训练样本:<span id="MathJax-Span-2" class="mrow"><span id="MathJax-Span-3" class="mo">{(x1,y1),(x2,y2),...,(xm,ym)}{(x1,y1),(x2,y2),...,(xm,ym)},其中<span id="MathJax-Span-39" class="mrow"><span id="MathJax-Span-40" class="mi">xx为输入向量,特征维度为<span id="MathJax-Span-42" class="mrow"><span id="MathJax-Span-43" class="mi">n_inn_in,而<span id="MathJax-Span-48" class="mrow"><span id="MathJax-Span-49" class="mi">yy为输出向量,特征维度为<span id="MathJax-Span-51" class="mrow"><span id="MathJax-Span-52" class="mi">n_outn_out。我们需要利用这m个样本训练出一个模型,当有一个新的测试样本<span id="MathJax-Span-58" class="mrow"><span id="MathJax-Span-59" class="mo">(xtest,?)(xtest,?)来到时, 我们可以预测<span id="MathJax-Span-72" class="mrow"><span id="MathJax-Span-73" class="msubsup"><span id="MathJax-Span-74" class="mi">ytestytest向量的输出。
如果我们采用DNN的模型,即我们使输入层有<span id="MathJax-Span-82" class="mrow"><span id="MathJax-Span-83" class="mi">n_inn_in个神经元,而输出层有<span id="MathJax-Span-88" class="mrow"><span id="MathJax-Span-89" class="mi">n_outn_out个神经元。再加上一些含有若干神经元的隐藏层。此时我们需要找到合适的所有隐藏层和输出层对应的线性系数矩阵<span id="MathJax-Span-95" class="mrow"><span id="MathJax-Span-96" class="mi">WW,偏倚向量<span id="MathJax-Span-98" class="mrow"><span id="MathJax-Span-99" class="mi">bb,让所有的训练样本输入计算出的输出尽可能的等于或很接近样本输出。怎么找到合适的参数呢?
如果大家对传统的机器学习的算法优化过程熟悉的话,这里就很容易联想到我们可以用一个合适的损失函数来度量训练样本的输出损失,接着对这个损失函数进行优化求最小化的极值,对应的一系列线性系数矩阵<span id="MathJax-Span-101" class="mrow"><span id="MathJax-Span-102" class="mi">WW,偏倚向量<span id="MathJax-Span-104" class="mrow"><span id="MathJax-Span-105" class="mi">bb即为我们的最终结果。在DNN中,损失函数优化极值求解的过程最常见的一般是通过梯度下降法来一步步迭代完成的,当然也可以是其他的迭代方法比如牛顿法与拟牛顿法。如果大家对梯度下降法不熟悉,建议先阅读我之前写的梯度下降(Gradient Descent)小结。
对DNN的损失函数用梯度下降法进行迭代优化求极小值的过程即为我们的反向传播算法。
本篇使用了矩阵向量求导,如果你对这一块不熟悉,请先阅读下我写的矩阵向量求导系列文章。
在进行DNN反向传播算法前,我们需要选择一个损失函数,来度量训练样本计算出的输出和真实的训练样本输出之间的损失。你也许会问:训练样本计算出的输出是怎么得来的?这 个输出是随机选择一系列<span id="MathJax-Span-107" class="mrow"><span id="MathJax-Span-108" class="mi">W,bW,b,用我们上一节的前向传播算法计算出来的。即通过一系列的计算:<span id="MathJax-Span-112" class="mrow"><span id="MathJax-Span-113" class="msubsup"><span id="MathJax-Span-114" class="mi">al=σ(zl)=σ(Wlal−1+bl)al=σ(zl)=σ(Wlal−1+bl)。计算到输出层第<span id="MathJax-Span-142" class="mrow"><span id="MathJax-Span-143" class="mi">LL层对应的<span id="MathJax-Span-145" class="mrow"><span id="MathJax-Span-146" class="msubsup"><span id="MathJax-Span-147" class="mi">aLaL即为前向传播算法计算出来的输出。
回到损失函数,DNN可选择的损失函数有不少,为了专注算法,这里我们使用最常见的均方差来度量损失。即对于每个样本,我们期望最小化下式:
其中,<span id="MathJax-Span-186" class="mrow"><span id="MathJax-Span-187" class="msubsup"><span id="MathJax-Span-188" class="mi">aLaL和<span id="MathJax-Span-191" class="mrow"><span id="MathJax-Span-192" class="mi">yy为特征维度为<span id="MathJax-Span-194" class="mrow"><span id="MathJax-Span-195" class="mi">n_outn_out的向量,而<span id="MathJax-Span-201" class="mrow"><span id="MathJax-Span-202" class="texatom"><span id="MathJax-Span-203" class="mrow"><span id="MathJax-Span-204" class="mo">||S||2||S||2为S的L2范数。
损失函数有了,现在我们开始用梯度下降法迭代求解每一层的<span id="MathJax-Span-218" class="mrow"><span id="MathJax-Span-219" class="mi">W,bW,b。
首先是输出层第<span id="MathJax-Span-223" class="mrow"><span id="MathJax-Span-224" class="mi">LL层。注意到输出层的<span id="MathJax-Span-226" class="mrow"><span id="MathJax-Span-227" class="mi">W,bW,b满足下式:
这样对于输出层的参数,我们的损失函数变为:
这样求解<span id="MathJax-Span-335" class="mrow"><span id="MathJax-Span-336" class="mi">W,bW,b的梯度就简单了:
注意上式中有一个符号<span id="MathJax-Span-435" class="mrow"><span id="MathJax-Span-436" class="mo">⊙⊙,它代表Hadamard积,对于两个维度相同的向量<span id="MathJax-Span-438" class="mrow"><span id="MathJax-Span-439" class="mi">A(a1,a2,...an)TA(a1,a2,...an)T和<span id="MathJax-Span-463" class="mrow"><span id="MathJax-Span-464" class="mi">B(b1,b2,...bn)TB(b1,b2,...bn)T,则<span id="MathJax-Span-488" class="mrow"><span id="MathJax-Span-489" class="mi">A⊙B=(a1b1,a2b2,...anbn)TA⊙B=(a1b1,a2b2,...anbn)T。
我们注意到在求解输出层的<span id="MathJax-Span-521" class="mrow"><span id="MathJax-Span-522" class="mi">W,bW,b的时候,有中间依赖部分<span id="MathJax-Span-526" class="mrow"><span id="MathJax-Span-527" class="mfrac"><span id="MathJax-Span-528" class="mrow"><span id="MathJax-Span-529" class="mi">&part;J(W,b,x,y)∂zL∂J(W,b,x,y)∂zL,因此我们可以把公共的部分即对<span id="MathJax-Span-546" class="mrow"><span id="MathJax-Span-547" class="msubsup"><span id="MathJax-Span-548" class="mi">zLzL先算出来,记为:
现在我们终于把输出层的梯度算出来了,那么如何计算上一层<span id="MathJax-Span-596" class="mrow"><span id="MathJax-Span-597" class="mi">L−1L−1层的梯度,上上层<span id="MathJax-Span-601" class="mrow"><span id="MathJax-Span-602" class="mi">L−2L−2层的梯度呢?这里我们需要一步步的递推,注意到对于第<span id="MathJax-Span-606" class="mrow"><span id="MathJax-Span-607" class="mi">ll层的未激活输出<span id="MathJax-Span-609" class="mrow"><span id="MathJax-Span-610" class="msubsup"><span id="MathJax-Span-611" class="mi">zlzl,它的梯度可以表示为:
如果我们可以依次计算出第<span id="MathJax-Span-715" class="mrow"><span id="MathJax-Span-716" class="mi">ll层的<span id="MathJax-Span-718" class="mrow"><span id="MathJax-Span-719" class="msubsup"><span id="MathJax-Span-720" class="mi">&delta;lδl,则该层的<span id="MathJax-Span-723" class="mrow"><span id="MathJax-Span-724" class="msubsup"><span id="MathJax-Span-725" class="mi">Wl,blWl,bl很容易计算?为什么呢?注意到根据前向传播算法,我们有:
所以根据上式我们可以很方便的计算出第l层的<span id="MathJax-Span-752" class="mrow"><span id="MathJax-Span-753" class="msubsup"><span id="MathJax-Span-754" class="mi">Wl,blWl,bl的梯度如下:
其中,第一个式子的推导可以参考机器学习中的矩阵向量求导(四) 矩阵向量求导链式法则中第三节的最后一个公式。
那么现在问题的关键就是要求出<span id="MathJax-Span-824" class="mrow"><span id="MathJax-Span-825" class="msubsup"><span id="MathJax-Span-826" class="mi">&delta;lδl了。这里我们用数学归纳法,第<span id="MathJax-Span-831" class="mrow"><span id="MathJax-Span-832" class="mi">LL层的<span id="MathJax-Span-834" class="mrow"><span id="MathJax-Span-835" class="msubsup"><span id="MathJax-Span-836" class="mi">&delta;LδL上面我们已经求出, 假设第<span id="MathJax-Span-841" class="mrow"><span id="MathJax-Span-842" class="mi">l+1l+1层的<span id="MathJax-Span-846" class="mrow"><span id="MathJax-Span-847" class="msubsup"><span id="MathJax-Span-848" class="mi">&delta;l+1δl+1已经求出来了,那么我们如何求出第<span id="MathJax-Span-855" class="mrow"><span id="MathJax-Span-856" class="mi">ll层的<span id="MathJax-Span-858" class="mrow"><span id="MathJax-Span-859" class="msubsup"><span id="MathJax-Span-860" class="mi">&delta;lδl呢?我们注意到:
可见,用归纳法递推<span id="MathJax-Span-964" class="mrow"><span id="MathJax-Span-965" class="msubsup"><span id="MathJax-Span-966" class="mi">&delta;l+1δl+1和<span id="MathJax-Span-973" class="mrow"><span id="MathJax-Span-974" class="msubsup"><span id="MathJax-Span-975" class="mi">&delta;lδl的关键在于求解<span id="MathJax-Span-980" class="mrow"><span id="MathJax-Span-981" class="mfrac"><span id="MathJax-Span-982" class="mrow"><span id="MathJax-Span-983" class="mi">&part;zl+1∂zl∂zl+1∂zl。
而<span id="MathJax-Span-999" class="mrow"><span id="MathJax-Span-1000" class="msubsup"><span id="MathJax-Span-1001" class="mi">zl+1zl+1和<span id="MathJax-Span-1008" class="mrow"><span id="MathJax-Span-1009" class="msubsup"><span id="MathJax-Span-1010" class="mi">zlzl的关系其实很容易找出:
这样很容易求出:
将上式带入上面<span id="MathJax-Span-1112" class="mrow"><span id="MathJax-Span-1113" class="msubsup"><span id="MathJax-Span-1114" class="mi">&delta;l+1δl+1和<span id="MathJax-Span-1121" class="mrow"><span id="MathJax-Span-1122" class="msubsup"><span id="MathJax-Span-1123" class="mi">&delta;lδl关系式我们得到:
现在我们得到了<span id="MathJax-Span-1248" class="mrow"><span id="MathJax-Span-1249" class="msubsup"><span id="MathJax-Span-1250" class="mi">&delta;lδl的递推关系式,只要求出了某一层的<span id="MathJax-Span-1255" class="mrow"><span id="MathJax-Span-1256" class="msubsup"><span id="MathJax-Span-1257" class="mi">&delta;lδl,求解<span id="MathJax-Span-1262" class="mrow"><span id="MathJax-Span-1263" class="msubsup"><span id="MathJax-Span-1264" class="mi">Wl,blWl,bl的对应梯度就很简单的。
现在我们总结下DNN反向传播算法的过程。由于梯度下降法有批量(Batch),小批量(mini-Batch),随机三个变种,为了简化描述,这里我们以最基本的批量梯度下降法为例来描述反向传播算法。实际上在业界使用最多的是mini-Batch的梯度下降法。不过区别仅仅在于迭代时训练样本的选择而已。
输入: 总层数L,以及各隐藏层与输出层的神经元个数,激活函数,损失函数,迭代步长<span id="MathJax-Span-1271" class="mrow"><span id="MathJax-Span-1272" class="mi">&alpha;α,最大迭代次数MAX与停止迭代阈值<span id="MathJax-Span-1274" class="mrow"><span id="MathJax-Span-1275" class="mi">ϵϵ,输入的m个训练样本<span id="MathJax-Span-1277" class="mrow"><span id="MathJax-Span-1278" class="mo">{(x1,y1),(x2,y2),...,(xm,ym)}{(x1,y1),(x2,y2),...,(xm,ym)}
输出:各隐藏层与输出层的线性关系系数矩阵<span id="MathJax-Span-1314" class="mrow"><span id="MathJax-Span-1315" class="mi">WW和偏倚向量<span id="MathJax-Span-1317" class="mrow"><span id="MathJax-Span-1318" class="mi">bb
1) 初始化各隐藏层与输出层的线性关系系数矩阵<span id="MathJax-Span-1320" class="mrow"><span id="MathJax-Span-1321" class="mi">WW和偏倚向量<span id="MathJax-Span-1323" class="mrow"><span id="MathJax-Span-1324" class="mi">bb的值为一个随机值。
2)for iter to 1 to MAX:
2-1) for i =1 to m:
a) 将DNN输入<span id="MathJax-Span-1326" class="mrow"><span id="MathJax-Span-1327" class="msubsup"><span id="MathJax-Span-1328" class="mi">a1a1设置为<span id="MathJax-Span-1331" class="mrow"><span id="MathJax-Span-1332" class="msubsup"><span id="MathJax-Span-1333" class="mi">xixi
b) for <span id="MathJax-Span-1336" class="mrow"><span id="MathJax-Span-1337" class="mi">ll=2 to L,进行前向传播算法计算<span id="MathJax-Span-1339" class="mrow"><span id="MathJax-Span-1340" class="msubsup"><span id="MathJax-Span-1341" class="mi">ai,l=σ(zi,l)=σ(Wlai,l−1+bl)ai,l=σ(zi,l)=σ(Wlai,l−1+bl)
c) 通过损失函数计算输出层的<span id="MathJax-Span-1379" class="mrow"><span id="MathJax-Span-1380" class="msubsup"><span id="MathJax-Span-1381" class="mi">&delta;i,Lδi,L
d) for <span id="MathJax-Span-1388" class="mrow"><span id="MathJax-Span-1389" class="mi">ll= L-1 to 2, 进行反向传播算法计算<span id="MathJax-Span-1391" class="mrow"><span id="MathJax-Span-1392" class="msubsup"><span id="MathJax-Span-1393" class="mi">&delta;i,l=(Wl+1)Tδi,l+1⊙σ′(zi,l)δi,l=(Wl+1)Tδi,l+1⊙σ′(zi,l)
2-2) for <span id="MathJax-Span-1438" class="mrow"><span id="MathJax-Span-1439" class="mi">ll = 2 to L,更新第<span id="MathJax-Span-1441" class="mrow"><span id="MathJax-Span-1442" class="mi">ll层的<span id="MathJax-Span-1444" class="mrow"><span id="MathJax-Span-1445" class="msubsup"><span id="MathJax-Span-1446" class="mi">Wl,blWl,bl:
2-3) 如果所有<span id="MathJax-Span-1518" class="mrow"><span id="MathJax-Span-1519" class="mi">W,bW,b的变化值都小于停止迭代阈值<span id="MathJax-Span-1525" class="mrow"><span id="MathJax-Span-1526" class="mi">ϵϵ,则跳出迭代循环到步骤3。
3) 输出各隐藏层与输出层的线性关系系数矩阵<span id="MathJax-Span-1528" class="mrow"><span id="MathJax-Span-1529" class="mi">WW和偏倚向量<span id="MathJax-Span-1531" class="mrow"><span id="MathJax-Span-1532" class="mi">bb。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号