颜色均摊段（ODT）学习笔记

其实我更喜欢叫她珂朵莉树，尽管这个东西和树没什么关系。

故事的一切起源于 CF896C Willem, Chtholly and Seniorious，本题基于随机数据，提出了一种理论复杂度错误，实际运行情况优异的算法。因为本题的题目背景，因此得名珂朵莉树，另外一个名字 Old Driver Tree （缩写 ODT）则是因为本题的出题人昵称为 ODT。当然，根据这种算法的特征，这个东西还有一个正式名字：颜色均摊段。

算法思想

对于数据结构题，我们有这样一种思路去维护：对于一个数列，我们把相同且连续的数字看成一个颜色段，然后对每个颜色段进行暴力操作，可以有效降低时间复杂度。但这种暴力是很好卡掉的，只需让颜色段尽可能多，算法就可以直接退化的 \(O(n^2)\)，甚至在随机数据下，这种算法的表现依然不是很好。

但在特定的情况下，当题目中的颜色段很少（例如：存在区间赋值操作且数据随机），这种算法就可以达到 \(O(n\log n)\) 等极好的时间复杂度，于是就诞生了使用 set 维护连续颜色段的算法。下文以 CF896C 作为模板题讲解这种算法。

写一个数据结构，支持以下操作：

1 l r x：将\([l,r]\) 区间所有数加上\(x\)
2 l r x ：将\([l,r]\) 区间所有数改成\(x\)
3 l r x ：输出将\([l,r]\) 区间从小到大排序后的第\(x\) 个数是的多少（即区间第\(x\) 小，数字大小相同算多次，保证 \(1\leq\) \(x\) \(\leq\) \(r-l+1\)）
4 l r x y ：输出\([l,r]\) 区间每个数字的\(x\) 次方的和模\(y\) 的值，即\(\left(\sum^r_{i=l}a_i^x\right)\)\(\bmod y\)。

其中 \(n,m\le 10^5\)，所有操作随机生成。

算法实现

珂朵莉树实际上是一个 set，set 中的每个节点都是一个颜色段，颜色段用结构体表示其内部信息。

struct cht{
	int l,r;
	mutable ll v;//mutable 用于快速修改颜色
	cht(int L,int R,ll V){l=L,r=R,v=V;}//变量类型有差异，所以要单独写初始化函数
	bool operator < (const cht &a)const {return l<a.l;}//默认按照颜色段左端点排序
};
typedef set<cht>::iterator iter;//迭代器，就是指针，接下来的各种操作都会常用
set<cht>s;

复杂度正确的部分

珂朵莉树的核心部分是 split（分裂）和 assign（覆盖）这两个函数函数，其时间复杂度均为单次 \(O(\log n)\)。

split

给定一个参数 \(x\)，split 函数负责返回 set 中以 \(x\) 为左边界的颜色段的位置（指针）。特别的，如果 \(x\) 位于颜色段 \(l,r\) 内，并非是端点，则将 \([l,r]\) 分裂为 \([l,x-1],[x,r]\) 并返回后者的指针；如果不存在 \(x\) 这个位置，则返回 set 的尾指针，一般我们习惯于在最后插入一个空节点减少特判。步骤其实十分简单：

找到 \(x\) 所在颜色段。
如果 \(x\) 是该颜色段的端点，直接返回指针。
否则分裂，返回分裂后的结果。

iter split(int pos){
	iter it=s.lower_bound(cht{pos,0,0});//查找颜色段
	if(it->l==pos)return it;//判断是否是端点，前面的特判是为了避免不存在 pos 导致 RE
	it--;//此时的 it 指向的颜色段包含 pos
	int L=it->l,R=it->r;ll V=it->v;
	s.erase(it);//分裂
	s.insert(cht{L,pos-1,V});
	return s.insert(cht{pos,R,V}).first; //insert 返回的 pair 的第一个参数是新插入的位置的迭代器
}

assign

区间推平操作，负责将一段区间赋为同一颜色。

我们要做的就是先分裂出以 \(l,r\) 为端点的颜色段，记为 \(s,t\)，然后将编号 \([s,t)\) 以内的所有颜色段删除，然后再插入一个以 \([l,r]\) 为端点的大颜色段。

set 支持删掉某个范围内的所有元素，调用 erase 即可删除 set 中所有位于 \([s,t)\) 的元素，且操作复杂度 \(O(\log n)\)。

void assign(int l,int r,ll k){
	iter itr=split(r+1),itl=split(l);//r+1 是因为 erase 函数遵循左闭右开原则
	s.erase(itl,itr);
	s.insert(cht{l,r,k});  
}

注意到我们先调用了对 \(r+1\) 分裂后再分裂了 \(l\)。这个顺序是不可改变的。因为具体解释比较麻烦，所以我盗了一张大佬的图（uid:43206）

原因图

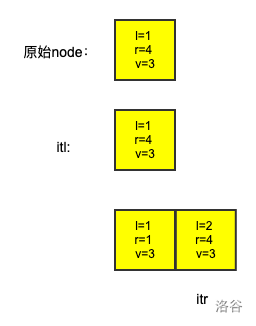
注意到调用先分裂 \(l\) 后再分裂 \(r+1\) 可能会导致 \(itl\) 原本指向的颜色段被删除分裂成两个，所以我们必须按照正确的顺序分裂。

复杂度不正确的部分

其实非常简单，就是分裂出左右颜色段，然后暴力遍历其中的所有颜色段.....

是的，就是这么简单，给出一份代码。

change(int l,int r,...){
    iter itr=split(r+1),itl=split(l);
	for(iter it=itl;it!=itr;it++){
		/*
        do something
        */
	}
    /*
    do something
    */
}

理论复杂度单次为 \(O(n)\)，随机数据下期望复杂度单次 \(O(\log n)\)，接下来会给出若干操作的事例。

区间加：

void add(int l,int r,ll k){
	iter itr=split(r+1),itl=split(l);
	for(iter it=itl;it!=itr;it++){
		it->v+=k;//可以直接改变结构体的成员是因为使用了 mutable
	}
	return;
}

区间第 \(k\) 小：

#define pli pair<ll,int>
#define mp make_pair
typedef long long ll;
pli bk[N];
int tot;
ll kth(int l,int r,int rk){
	tot=0;
	iter itr=split(r+1),itl=split(l);
	for(iter it=itl;it!=itr;it++){
		bk[++tot]=mp(it->v,it->r-it->l+1);
	} 
	sort(bk+1,bk+1+tot);
	for(int i=1;i<=tot;i++){
		if(rk<=bk[i].second)return bk[i].first;
		rk-=bk[i].second;
	}
    return -1;
}

区间幂的和：

这个操作实际上复杂度是 \(O(\log^2 n)\) 的。

ll ksm(ll a,ll b,ll p){
	ll ans=1;
	while(b){
		if(b&1)ans=(ans*a)%p;
		a=(a*a)%p;
		b>>=1;
	}
	return ans;
}
ll pow_sum(int l,int r,ll x,ll y){
	iter itr=split(r+1),itl=split(l);
	ll res=0;
	for(iter it=itl;it!=itr;it++){
		res+=(it->r-it->l+1)*ksm(it->v%y,x,y)%y;
        res%=y;
	} 
    return res;
}

然后这题就做完了，提交记录。

时间复杂度

理论复杂度单次为 \(O(n^2)\)，随机数据下期望复杂度 \(O(n\log n)\)，具体不会证明。

例题讲解

P5350 序列

这个题正解好像是较为诡异的可持久化平衡树，但因为数据太水被发现 ODT 加 O2 可以草过去于是变成了 ODT 的一大模板题。

前三个操作可以用 ODT 随便做。

复制操作可以记录两个区间的下标差，删掉区间 \([l_2,r_2]\) 一个一个取出 \([l_1,r_1]\) 内的颜色段，修改下标后插入 set 即可。

交换操作最为复杂，我们必须先将 \([l_1,r_1]\) 内的所有颜色段拷贝下来后，删掉这个 \([l_1,r_1]\)，然后将 \([l_2,r_2]\) 内的颜色段复制过去，在将拷贝的部分复制到 \([l_2,r_2]\) 的位置上，这里需要注意，操作前必须满足 \(l_1<l_2\)，不满足就要调整；原因在于 set 所操作的区间均为左闭右开，若先操作后面的区间，会导致前面的区间的右边界向前移动，而右边界是开的，所以会少插入数。但如果始终先操作前面的区间，会导致后面的区间的左边界向后移动，而左边界是闭的，所以不会少插入，详细可以看这里，由此，对于两个区间的操作，我们需要慎重考虑操作的顺序。

翻转操作比较简单，记一个区间 \([l,r]\) 在区间 \([L,R]\) 翻转后翻到了区间 \([l',r']\)，注意到翻转前后区间关于 \(\dfrac{L+R}{2}\) 对称，所以可以得到 \(l'=L+R-r,r'=L+R-l\)，拷贝下来后再插回去就做完了。

时间复杂度是 \(O(跑的过)\)。record。

[ABC371F] Takahashi in Narrow Road

省选 2025 D2T1 严格弱化版。

记录每个人的位置 \(x_i\)，注意到每次操作完后，会有一段区间的 \(x_i\) 呈单调上升趋势，且相邻两项差为 \(1\)。不好做，我们令 \(a_i\gets a_i-i\)，则就变成了每次操作会让一段区间的 \(x_i\) 变成同一个值，所以找到对应块后直接暴力推就可以，因为只有 split 每次多分裂一个块，而没暴力推一次，都会减少一个块，所以所有操作中颜色段变化数为 \(n\) 级别的，所以珂朵莉树复杂度是正确的，时间复杂度 \(O(n\log n)\)。

P8512 [Ynoi Easy Round 2021] TEST_152

有意思的题，先不思考询问，单纯从前往后把 \(n\) 个操作推一遍，发现可以用上一题的方法，且所有操作中颜色段变化数为 \(n\) 级别的，一个颜色段对答案的贡献即为颜色乘长度。考虑加上区间限制，套路进行扫描线，当扫到区间 \(r\) 时，考虑减去 \([1,l-1]\) 操作的影响。一个颜色只会被它后面染上的颜色所覆盖，所以只需要计算每个 \([1,l-1]\) 的颜色段在扫到 \(r\) 时还对答案有多少贡献。

考虑维护时间轴，时间轴上的第 \(i\) 个位置表示，当前扫到 \(r\)，操作 \(i\) 对答案剩下的贡献，若用第 \(i\) 个颜色去覆盖序列，则在时间轴位置 \(i\) 加上 \((r_i-l_i+1)\times v_i\)，若颜色 \(i\) 被其他颜色覆盖，则在时间轴位置 \(i\) 加上 \(-len\times v_i\)，\(len\) 表示被覆盖的区间长度。

扫描线时要对时间轴单调加，处理询问时要对时间轴区间和，所以用树状数组维护时间轴，珂朵莉树复杂度同上一题，总时间复杂度 \(O(n\log n)\)。record。

The End

一些闲话。

最近集训时发现很多同学都在学珂朵莉树，恍惚间想起自己去年（2024.10.4）貌似写过一次 ODT 的学习笔记，但并没有特别认真。到了暑假，又尝试给原版的文章优化了一下，增添了几道例题。

当我再次再晚上听末日三问的片头曲，思绪又不由得带回到了去年的夏天，第一句歌词所带来的穿透力仍然没有减弱。最近也打算补完这个系列的轻小说部分，~~虽然对剧情的一言难尽略有耳闻，不过还是打算鼓足勇气看完~~。

时至今日，我还会像过去一样说出“我永远喜欢珂朵莉”这样的话吗？我自己也不知道答案，其实无所谓了，毕竟觉得自己对这个系列的热情还没有消散，最后的最后还是放一张朋友圈的背景图。

珂（图片来源 bilibili）

还是趁早睡吧，最近可能会整理一些远古的博客，~~大部分都因为我去年摆烂到现在都没整理~~。

upd by 2025.7.14

posted @ 2025-07-14 01:26 zuoqingyuan111 阅读(28) 评论(0) 收藏举报

刷新页面返回顶部

zuoqingyuan