OIFC 2025-11-11

难度评估

1. 上位绿~下位蓝。
2. 蓝~紫
3. 紫（有原题）
4. 紫~黑

A

题目：给定一个序列，要求分为若干个子序列（子序列代表这个序列在原数组也是连续的），其中每个子序列为 \(S_i\)，要求求出有多少种划分方法满足：

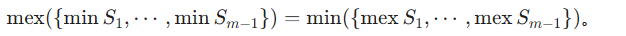
Tag：DP，计数，数学。

由于最开始我理解错了 Mex 导致浪费了大概两个小时。

可以先思考 Mex 的性质：一个序列的 Mex 为 x 说明这个序列中包含 1~x-1 的中的所有数。

由于有这个性质，我们可以从 minmex 开始考虑。

由于 0 在 Mex 里面是个很特殊的东西，所以我们先考虑当没有 0 的情况下，那么由于 minmex = 0，而且 mexmin 也一定为 0，所以随便选就行了。

然后考虑如果在有 0 的情况下 minmex 还是 0，那么就说明有一个集合没有 0，这样的话 mexmin 就分两种情况：

1. 没有 0 的那个集合的最小值为 1，那么 mexmin 就是 2
2. 没有 0 的那个集合的最小值不为 1，那么 mexmin 就是 1

可以发现以上两种做法的 mexmin 都不等于 minmex，所以可以得出结论每个子序列都一定有 0.

这样的话 mexmin = 1，注意到需要 minmex = mexmin，那么 mexmin 也需要为 1.

这就需要至少有一个子序列没有 1.

总结：所有子序列都有0，而且有至少一个没有1

于是我们考虑如何实现这个做法，我们可以考虑反着来，求出有多少个子序列都有 0 而且全都有 1 的情况，再用所有子序列都有 0 去减。

可以考虑令 dp[i][1/0][1/0] 为到第 i 和 i+1 的间隔（这个时候没有决定是否放置一个间隔吧 i 和 i+1 分开），放不放 0，放不放 1.

转移参考代码。

代码（A）

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 15112009;
int qpow(int a, int b) {
	int res = 1;
	while (b) {
		if (b % 2 == 1) res *= a;
		a *= a;
		a %= mod;
		res %= mod;
		b /= 2;
	}
	return res;
}
int n, a[1000005];
int ny(int x) {
	return qpow(x, mod - 2);
}
int b[1000005];
int dp[1000005][3][3];
signed main() {
//	ios::sync_with_stdio(false);
//	cin.tie(0); cout.tie(0);
	freopen("16.in", "r", stdin);
	freopen("decryption.out", "w", stdout);
//	cout << qpow(3, 4);
	cin >> n;
	int minn = 1e18, maxn = 0;
	for (int i = 1; i <= n; i ++) cin >> a[i], minn = min(minn, a[i]), maxn = max(maxn, a[i]);
	if (minn > 0) {
		cout << qpow(2, n - 1) << "\n";
		return 0;
	}
	if (n <= 15) {
		int cnt = 0;
		int cnt1 = 0, cnt2 = 0;
		int maxbi = (1ll << (n - 1));
		for (int tp = 0; tp < maxbi; tp ++) {
			for (int i = 1; i <= n; i ++) b[i] = 0;
			int x = tp, tc = 1;
			while (x) {
				b[tc] = x % 2;
				x /= 2;
				tc ++;
			}
			b[n] = 1;
			vector <int> v, mins;
			int mm = 1e18;
//			for (int i = 1; i <= n; i ++) cout << b[i] << " "; cout << "\n";
			for (int i = 1; i <= n; i ++) {
				v.push_back(a[i]);
//				cout << "!!!!\n" << endl;
				if (b[i]) {
					int nme = 0;
					if (!v.size()) continue;
					sort(v.begin(), v.end());
					int lst = -1;
					v.push_back(1e18);
					for (auto x : v) {
						if (x - lst > 1) {
							nme = lst + 1;
							break;
						}
						lst = x;
					}
					mm = min(mm, nme);
					mins.push_back(*v.begin());
					v.clear();
				}
			}
			sort(mins.begin(), mins.end());
			int lst = -1;
			int mmm = 0;
			mins.push_back(1e18);
			for (auto x : mins) {
				if (x - lst > 1) {
					mmm = lst + 1;
					break;
				}
				lst = x;
			}
			if (mmm == mm) {
				cnt ++;
				if (mm == 1) cnt1 ++;
				else cnt2 ++;
//				cout << mm << "\n";
//				for (int i = 1; i <= n; i ++) cout << b[i] << " "; cout << "\n";
			}
//			cout << mmm << " " << mm << "\n"; 
		}
		cout << cnt;
		return 0;
	}
	int cnt = 0, ans = 1;
	int f0 = 0, l0 = n;
	for (int i = 1; i <= n; i ++) {
		if (a[i] == 0) {
			f0 = i;
			break;
		}
	}
	for (int i = 1; i <= n; i ++) {
		if (a[i] == 0) {
			l0 = i;
		}
	}
	cnt = 1;
	for (int i = f0 + 1; i <= l0; i ++) {
		if (!a[i]) {
			ans *= (cnt + 1);
			ans %= mod;
			cnt = 1;
		}else
		cnt ++;
	}
//	cout << ans << "\n";
	dp[0][0][0] = 1;
	for (int i = 1; i <= n; i ++) {
		if (a[i] == 0) {
			dp[i][0][0] = dp[i - 1][1][1] + dp[i - 1][0][1];
			dp[i][1][0] = dp[i - 1][0][0] + dp[i - 1][1][0];
			dp[i][1][1] = dp[i - 1][1][1] + dp[i - 1][0][1];
		} else if (a[i] == 1) {
			dp[i][0][1] = dp[i - 1][0][1] + dp[i - 1][0][0];
			dp[i][1][1] = dp[i - 1][1][1] + dp[i - 1][1][0];
			dp[i][0][0] = dp[i - 1][1][1] + dp[i - 1][1][0];			
		} else {
			dp[i][0][0] = dp[i - 1][1][1] + dp[i - 1][0][0];
			dp[i][0][1] = dp[i - 1][0][1];
			dp[i][1][0] = dp[i - 1][1][0];
			dp[i][1][1] = dp[i - 1][1][1];
		}
		dp[i][0][0] %= mod;
		dp[i][0][1] %= mod;
		dp[i][1][0] %= mod;
		dp[i][1][1] %= mod;
	}
	cout << (ans - dp[n][1][1] + mod) % mod;
	return 0;
}