Educational Codeforces Round 133 (Rated for Div. 2)
加粗：赛时AC
普通：赛后AC
A. 2-3 Moves
目标是1特判，对于其他的样例n，我们每次都先3格3格的走。
如果n%3==0，那么刚好走完。
如果n%3==1，那么我们可以撤回一个3，改走两个2。
如果n%3==2，那么我们再走一个2.
int main() { int T; cin>>T; while(T--) { cin>>n; if(n==1) { cout<<2<<endl; continue; } if(n%3) cout<<n/3+1<<endl; else cout<<n/3<<endl; } return 0; }
B. Permutation Chain
第一次一定会造成两个错位，其他的每次造成一个错位，符合这种方式的，怎么搞都行。
int main() { ll T; read(T); while(T--) { read(n); for(int i=1;i<=n;i++) a[i]=i; cout<<n<<endl; printing(a); for(int i=n;i>1;i--) { if(i==n) swap(a[1],a[n]); else swap(a[i],a[i+1]); printing(a); } } return 0; }
C. Robot in a Hallway
细节有些多。
我的想法是我们首先有一个正常的走蛇形到终点线，除此之外，当我们走完某列之后，我们可以从下一列的第一个位置开始，剩下的位置走一个大回环。（对于初始状况，我们假定0还没走过，然后直接走一个大回环）
如上图，但是有些列走完是从上到下回环，有些则是从下到上回环。
我们第一次先蛇形跑完，然后记录每个点的到达时间为基础到达时间，也就是踩上这个位置的时间。然后对于每个我们刚好跑完某一列的位置，我们从下个位置跑大回环，然后统计最小的答案，它的实际情况并不会很多，但是如何去统计这个答案是个问题。
我的方法是这样的，对于下一个位置，我们是当前时间+1，下下个位置则是当前时间+2，假设我们到开始回环的位置的时间足够我们不停留的向前冲到终点，那么每个位置对我们开始回环的位置都有一个限制，我们记录还没跑完的格子中限制最大的，更新恰好能直接通过它的最大时间，那么答案就是现在的时间+还没通过的格子数，这个最大限制位置我们可以用一个ST表进行维护，也可以直接用每个点进行一个倒推。
inline void ycl() { for(ll i=0;i<=19;i++) { for(ll j=0;j<=cnt;j++) { ST1[j][i]=0; } } for(ll i=1;i<=cnt;i++) ST1[i][0]=counting[i]; for(ll i=1;i<=19;i++) { for(ll j=1;j+(1<<i)-1<=cnt;j++) { ST1[j][i]=max(ST1[j][i-1],ST1[j+(1<<(i-1))][i-1]); } } } inline ll query(ll l,ll r) { ll len=(ll)(log2(r-l+1)); return max(ST1[l][len],ST1[r-(1<<len)+1][len]); } int main() { ll T; read(T); mov[0]={1,0};mov[1]={0,1};mov[2]={-1,0};mov[3]={0,1}; while(T--) { read(n); for(ll i=1;i<=2;i++) { for(ll j=1;j<=n;j++) { read(a[i][j]); G[i][j]=0; } } ll tim=0,nown=1,nowi=1,nowtim=0; cnt=0; ll ans=0; G[1][1]=0; while(nown<=n) { pair<ll,ll> lim=mov[tim%4]; nowi+=lim.first;nown+=lim.second; G[nowi][nown]=max(nowtim+1,a[nowi][nown]+1);//�������λ�õ���Сʱ�� tim++; nowtim=max(G[nowi][nown],tim); } if(n%2==1) ans=G[2][n]; else ans=G[1][n]; ac[0]=-1; counting[++cnt]=-1; ac[1]=0; for(ll i=2;i<=n;i++) { ++cnt; counting[cnt]=a[1][i]-cnt+1; ac[cnt]=G[1][i]; } for(ll i=n;i>=1;i--) { ++cnt; counting[cnt]=a[2][i]-cnt+1; ac[cnt]=G[2][i]; } ycl(); ll l=1,r=cnt; while(l<=r) { ans=min(ans,max(ac[l-1],query(l,r)+(l-1))+(r-l+1)); l+=2;r-=2; } cnt=0; ac[0]=G[2][1]; for(ll i=2;i<=n;i++) { ++cnt; counting[cnt]=a[2][i]-cnt+1; ac[cnt]=G[2][i]; } for(ll i=n;i>=2;i--) { ++cnt; counting[cnt]=a[1][i]-cnt+1; ac[cnt]=G[1][i]; } ycl(); l=1,r=cnt; while(l<=r) { ans=min(ans,max(ac[l-1],query(l,r)+(l-1))+(r-l+1)); l+=2;r-=2; } printf("%lld\n",ans); } return 0; }
D. Chip Move（DP以及优化）
早知道先切这题了。。。
我们设dp(i,j),其中i为当前跳到的位置，j为已经跳了几步到这个位置，那么跳到这一位之前的步长为j+k，那么我们考虑dp(i,j)由哪些状态而来。
假设上一跳已经跳了，跳到了i-(j+k)，那么答案被记录在dp(i-(j+k),j)里面，但实际上上一跳跳的是(j+k)的倍数，也就是说它也能跳到dp(i,j)上，因此dp(i,j)+=dp(i-(j+k),j)。
假设上一跳还没跳，那么它由i-(j+k)这个位置第一次跳到，dp(i,j)+=dp(i-(j+k),j-1)。
对于时间的优化，i是无法优化的，假设我们从0起跳跳到2e5，令1+2+3+...+n<=2e5,得到的答案在700以内，也就是我们的总跳数不会超过700.
对于空间我们的DP只和上一层有关，显然使用滚动数组优化。
int main() { read(n);read(k); dp[0][0]=1; int cur=0; for(int j=0;j<=630;j++) { cur^=1; for(int i=0;i<=n;i++) { dp[i][cur]=0; if(i-(j+k)>=0) dp[i][cur]=dp[i-(j+k)][cur]+dp[i-(j+k)][cur^1]; dp[i][cur]%=MOD; ans[i]+=dp[i][cur];ans[i]%=MOD; } } for(int i=1;i<=n;i++) printf("%lld ",ans[i]); return 0; }
E. Swap and Maximum Block（线段树+状压思想）
来自官方题解：
我们利用类似于线段树的方式去维护我们的序列，那么对于某次的转换k，实际上是从下往上(最后一层设为0)第k+1层的两个叶子节点的互换。
我们用线段树维护我们的前缀和、后缀和、区间和以此向上得到区间最大子段和，类似分治求最大子段和。
可以发现两个事实：
当我们对某一层进行两次操作的时候，相当于没有改变。
当我们对某一层进行操作的时候，我们维护的值会对其祖先节点维护的值产生影响，但不会对其孩子节点维护的值产生影响。
那么我们对于某一层进行变化，可能产生的结果是以2为底的数量级增长，例如对于第0层，所拥有的状态数就是1，而第1层就会产生两种状态，第二层就会有4种状态(交换第2层、交换第1层、都交换以及不变)。
这样我们就可以使用类似状压的方式直接把状态保存下来，最终得到答案，总的状态数为O(n*2n)量级
struct node { ll sum,pref,suff,ans; node (node &l,node &r) { sum=l.sum+r.sum; pref=max(l.pref,l.sum+r.pref); suff=max(r.suff,r.sum+l.suff); ans=max(max(l.ans,r.ans),l.suff+r.pref); } node (ll x) { sum=x; pref=suff=ans=max(x,1ll*0); } node (){}; }; vector<node> tr[N*4]; inline void build(ll v,ll l,ll r) { tr[v].resize(r-l); //这个函数可以使vector像数组一样使用而不是push_back if(l==r-1) tr[v][0]=node(a[l]); else { ll mid=(l+r)>>1; build(v*2,l,mid); build(v*2+1,mid,r); for(int i=0;i<mid-l;i++) { tr[v][i]=node(tr[v*2][i],tr[v*2+1][i]); tr[v][i+(mid-l)]=node(tr[v*2+1][i],tr[v*2][i]); } } } int main() { read(n); ll m=(1<<n); for(int i=0;i<m;i++) read(a[i]); build(1,0,m); ll q; read(q); ll cur=0; while(q--) { ll x; read(x); cur^=(1<<x); cout<<tr[1][cur].ans<<endl; } return 0; }
F. Bags with Balls(斯特林数)
思路来自官方题解下方评论区(官方的看不懂)
我们先列出基础的公式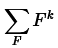
利用斯特林数对其变为下降幂有：
对于红色部分，我们用组合的方式进行思考，相当于在有F个箱子取出奇数球的情况下，再从中选择i个球的方案数。
那么这个式子也就等价于先选择i个箱子，在i个箱子中取出奇数球，其他箱子不管的方案数，即红色部分=$\binom{n}{i}m^{n-i}\left\lceil{m\over 2}\right\rceil^i$
带入上式得
$$\begin{aligned} \sum\limits_{i=0}^k S(k,i)n^{\underline i}m^{n-i}\left\lceil{m\over 2}\right\rceil^i \end{aligned}$$
最终复杂度只有O(k2)
我只能说这个思路简直nb。
inline void ycl() { S[0][0]=1; for(int i=1;i<=2020;i++) { for(int j=1;j<=2020;j++) { S[i][j]=S[i-1][j-1]+j*S[i-1][j]; S[i][j]%=MOD; } } } inline ll ksm(ll a,ll b) { ll lim=1,bas=a; while(b) { if(b&1) { lim*=bas; lim%=MOD; } bas*=bas; bas%=MOD; b>>=1; } return lim%MOD; } int main() { ycl(); read(T); while(T--) { read(n);read(m);read(k); ll ans=0,nd=1; for(int i=1;i<=min(n,k);i++) ////为了保证下降幂正确i从1开始 { nd*=(n-i+1)%MOD; nd%=MOD; ll lim=S[k][i]%MOD*nd%MOD*ksm(m,n-i)%MOD*ksm((m+1)/2,i)%MOD; lim%=MOD; ans+=lim; ans%=MOD; } printf("%lld\n",ans); } return 0; }
