Codeforces Round #810 (Div. 2)

加粗:赛时AC
普通:赛后AC
A. Perfect Permutation
签到题,将数组循环左移一位得到符合条件数组。
B. Party
思维题。当m是偶数的时候,我们可以把所有人都请来。
当m是奇数的时候,我们证明:最多只有两个人无法到场。
为了让边数变回偶数,我们需要删除一些人,记录所有人的度:
如果只不邀请一个人,那这个人的度数一定是奇数。
如果不邀请两个人,在两个人有一条边的情况下,两人的度应该都要是偶数。如果两人没有边是无效删除。
如果不邀请三人及以上,考察这三个人的度的关系,会发现不优于以上两种,由此得证。

int main() { read(T); while(T--) { read(n);read(m); for(int i=1;i<=n;i++) { deg[i]=0; read(a[i]); } for(int i=1;i<=m;i++) { ll lima,limb; read(lima);read(limb); u[i]=lima; v[i]=limb; deg[lima]++;deg[limb]++; } if(m%2==0) { cout<<0<<endl; continue; } ll ans=10000000000; for(int i=1;i<=n;i++) if(deg[i]%2==1) ans=min(ans,a[i]); for(int i=1;i<=m;i++) { if(deg[u[i]]%2==0&°[v[i]]%2==0) { ans=min(ans,a[u[i]]+a[v[i]]); } } cout<<ans<<endl; } return 0; }
C. Color the Picture
某种意义上来说比B好写。
根据定义,对于整体来说,我们涂的时候必须要选定一个方向(横或竖),并且涂的时候要保证每种颜色能够涂的行数是2行及以上,因此要特判一下只剩一行或者一列的情况。

inline bool judrow() { bool ff=0; ll limn=n; for(int i=1;i<=k;i++) b[i]=a[i]; sort(b+1,b+1+k); for(int i=k;i>=1;i--) { if(b[i]<2*m) return 0; ll tim=b[i]/m; if(tim>2) ff=1; if(limn==1) return ff; limn-=tim; if(limn<=0) return 1; } return 0; } inline bool judcol() { bool ff=0; ll limn=m; for(int i=1;i<=k;i++) b[i]=a[i]; sort(b+1,b+1+k); for(int i=k;i>=1;i--) { if(b[i]<2*n) continue ; ll tim=b[i]/n; if(tim>2) ff=1; if(limn==1) return ff; limn-=tim; if(limn<=0) return 1; } return 0; } int main() { read(T); while(T--) { read(n);read(m);read(k); for(int i=1;i<=k;i++) read(a[i]); sort(a+1,a+1+k); if(a[k]>=n*m) cout<<"Yes"<<endl; else if(judcol()||judrow()) cout<<"Yes"<<endl; else cout<<"No"<<endl; } return 0; }
D. Rain(两重差分)
首先我们如果用横坐标作为地区,纵坐标作为积水量,那么每一场雨的函数都是离散的先升后降的折线。
由于这条折线的斜率为±1,因此我们可以选用两重差分数组进行维护。
对于折线的左起点,我们在第二重差分数组对其下一个位置+1,第一重差分数组从左起点开始积累一个1,原数组就会持续+1。
对于顶点位置,我们在第二重差分数组其下一个位置-2,第一重差分数组从顶起点开始就会变成一个-1。
最后对于右终点我们在第二重差分数组其下一个位置+1,最后第一重差分数组就会变为0,该段的影响恢复。
样例一如图所示。
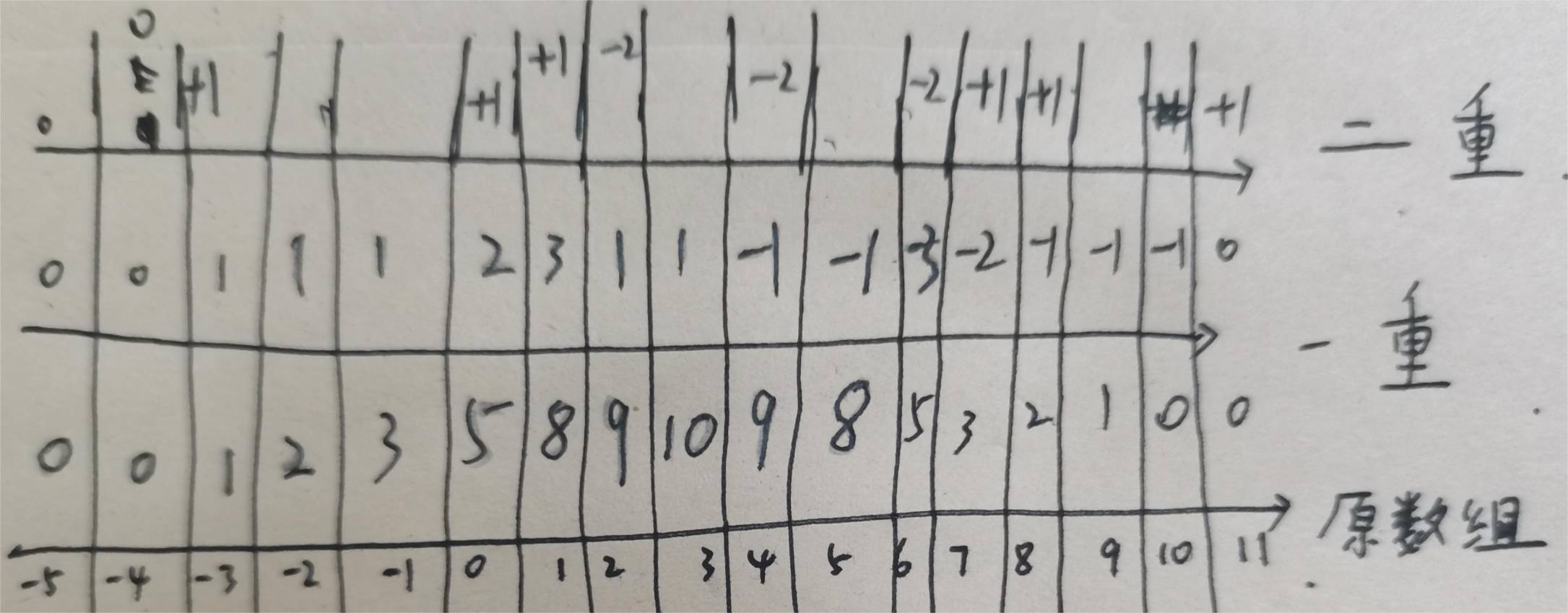
下一个问题:我们的横坐标接近无限长,如何计算积水量?
我们证明一点:在其他位置的答案一定不优于在顶点位置的答案。
我们可以考察两条折线相交的情况,画个图其实很容易就能够证明出来,并且相同的思路可以推广到多个折线。
有了以上结论,我们就可以用类似离散化的思想从左到右去计算所有顶点位置的积水量。
最后一个问题:如何判断删除该折线能够得到答案?
假设我们有一个位置pos的积水量aj大于m,那么对于某天的xi和pi:
如果pos在xi的右边,那么有pi-xi+pos<=aj-m.
如果pos在xi的左边,那么有pi+xi-pos<=aj-m.
但是超过m的顶点可能不止一处,我们可以对式子进行变换:
pi+xi<=aj-m+pos
xi-pi>=pos+m-aj 然后统计最大的aj-m+pos和最小的pos+m-aj即可
我们枚举的xi和pi满足上不等式就能够符合题意。

inline void upd(ll pos,ll val) { if(val<=m) return ; maxx=max(maxx,pos+val-m); //如果在左边有超过的 minn=min(minn,pos-val+m); //如果在右边有超过的 } inline void solve() { maxx=-10000000000;minn=10000000000; vec.clear(); vec.push_back({-10000000000,0}); read(n);read(m); for(int i=1;i<=n;i++) { read(x[i]);read(p[i]); vec.push_back({x[i]-p[i]+1,1}); vec.push_back({x[i]+1,-2}); vec.push_back({x[i]+p[i]+1,1}); } sort(vec.begin(),vec.end()); ll pre=0,cha1=0,cha2=0; for(int i=1;i<vec.size();i++) { pii=vec[i]; pii2=vec[i-1]; if(i!=1) { pre=pre+(pii.first-pii2.first)*cha1; //当前峰值 upd(pii.first-1,pre); //顶点的可能位置 } cha1+=pii.second; } for(int i=1;i<=n;i++) { if(x[i]-p[i]<=minn&&p[i]+x[i]>=maxx) printf("1"); else printf("0"); } printf("\n"); } int main() { read(T); while(T--) solve(); return 0; }
E. XOR Triangle(数位DP)
思路来自:https://zhuanlan.zhihu.com/p/546016199,自己推理了一下,加深了对数位DP的理解,十分感谢!
设x=a^b,y=b^c,z=a^c,这是三条边的值。
以逆向思考去考虑一个三角形,那么就要符合两边之和小于最长边(其余边之和大于最长边是能形成多边形的充要条件)。
即x+y<=z或x+z<=y或y+z<=x。
又通过计算可以知道x、y、z两两异或可以等于另一个值,即x^y^z=0.
从而有z=x^y<=x+y<=z以此类推
因此不符合的答案要满足x^y==x+y.
又有x+y==(x|y)+(x&y)、x^y=(x|y)-(x&y)
从而xy应符合x&y==0,即存在两个非最大边每一位上都没有两个1同时出现的时候,答案符合要求。
设状态dp(i,s1,s2),i代表的是目前考虑到了第i位,s1与s2取000(2)~111(2),s1表示的是a\b\c是否在这一位之前的前缀与n的前缀相等(是为1,否为0),用于控制状态上界。
s2表示这之前的x\y\z是否符合前缀全为1,或者在某一位不为1的时候,x\y\z三个数字在这一位都是0的状态(是为1,否为0)。
我们每一次都枚举一个s为000(2)~111(2),表示这一位我们a\b\c的取值,如果出现了s1&s!=0并且n的该位是0的情况,就意味着我们在某一个未知数上的取值超过了上界n,这个时候就不能转移。
当n该位的值是1的时候,s1&s为1的状态都能够被传递到。当n该位的值是0的时候,只能够传递到s1的状态。(对于s1的解释)
当我们固定了某个边的前缀的时候,如果在这个边依旧选取的是1,对于另外两个边,如果满足在该位上是一个0和一个1的分布,这种情况就符合题意,那么就能将该状态传递下去,如果三个边都选取的是0,也能够传递下去,由于异或的性质,不存在该位三个都是1的情况。
实际上s2就是在控制最大的边的位置,若s2出现一位1,那一位就是最大的边的位置,要求剩下的两个位置不能同时出现1。而s2出现两位1就是一个等腰三角形(在这一位之前),出现三个1的时候是等边三角形(在这一位之前),而如果没有1的存在,那么两边之和大于第三边。(对于s2的解释)
每次都只和上一位有关,可以使用滚动数组。
将所有的边的可能性减掉非法可能就是最终答案。

inline int getNext(int s2,int p) { int lim=0; int a=p&1,b=(p>>1)&1,c=(p>>2)&1; if(a^b) lim+=1; if(b^c) lim+=2; if(a^c) lim+=4; if(lim==0) lim=7; return lim&s2; } int main() { cin>>s; dp[0][7][7]=1; for(int i=0;i<s.size();i++) { totunm=totunm*2; totunm=(s[i]=='0') ? totunm : totunm+1; totunm%=MOD; for(int s1=0;s1<=7;s1++) { for(int p=0;p<=7;p++) { if((s1&p)&&s[i]=='0') continue; for(int s2=0;s2<=7;s2++) { ll next=getNext(s2,p); if(!next) continue; if(s[i]=='1') { dp[i+1][s1&p][next]+=dp[i][s1][s2]; dp[i+1][s1&p][next]%=MOD; } else { dp[i+1][s1][next]+=dp[i][s1][s2]; dp[i+1][s1][next]%=MOD; } } } } } totunm++; totunm%=MOD; ll ans=totunm%MOD*totunm%MOD*totunm%MOD; for(int i=0;i<=7;i++) { for(int j=0;j<=7;j++) { ans=ans-dp[s.size()][i][j]; ans=(ans+MOD)%MOD; } } printf("%lld\n",ans%MOD); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号