Codeforces Round #785 (Div. 2)

加粗:赛时AC
普通:赛后AC
A. Subtle Substring Subtraction
水题,偶数Alice选完,奇数少选一个,然后和Bob比较
B. A Perfectly Balanced String?
根据题意,循环字符串符合题目的条件,判断字符串是不是循环字符串的一部分即可。
C. Palindrome Basis
回文数的个数十分有限,全部找出来然后做完全背包就行了。
嗯我没想出来,别骂了(

#include<cstdio> #include<iostream> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<map> #include<vector> #include<queue> #include<iterator> #include<set> #define N 40010 #define ll long long using namespace std; int T,tot,n; const ll MOD=1e9+7; int p[N]; ll f[N]; //快读 inline void read(int &p) { p=0; int f=1;char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9') p=p*10+(ch-'0'),ch=getchar(); p*=f; } inline bool check(int x) { int lim=0,limx=x; int p=1; while(limx) { lim=lim*10+(limx%10); limx/=10; } if(x==lim) return 1; else return 0; } inline void ycl() { for(int i=1;i<=40000;i++) if(check(i)) p[++tot]=i; } int main() { ycl(); read(T); f[0]=1; for(int i=1;i<=tot;i++) { for(int j=0;j<=40000;j++) { if(p[i]>j) continue; f[j]+=f[j-p[i]]; f[j]%=MOD; } } while(T--) { read(n); printf("%lld\n",f[n]); } return 0; }
D. Lost Arithmetic Progression
思维+数学,这题十分考验思考的细节,做的时候手推几个特例会有助于思考
记住首项和公差和项数可以确定一个数列,这之后我们所有的推导都要建立在确定两个或者三个数列的首项和公差关系的基础上。
然后我们一步一步来。
一、首先我们确定A什么情况下存在
(1).b <= c
(2).b+(y-1)q>=c+(z-1)r
(3).r%q == 0
(4).(c-b)%q == 0
确定存在性实际上就是确定C是B的一部分的合法性,通过以上的首项公差关系我们可以确定存在关系,同理A也一定有以上性质。
二、确定A是否有限
(1).b<=c-r
(2).b+(y-1)q>=c+zr
也就是B里面要包含C对应的无限数列的上一项和下一项,因为假如B不包含的话,A就可以包含C对应的无限数列的前无限项以及后无限项,就会产生无数个。
三、确定A的个数
根据题目的定义,设A=[a,p,x]
(1).a>c-r
(2).a+(x-1)p<c+zr
(3).(a-c)%p==0
(4).lcm(p,q)==r
前三个前面有原因,第四个由于C是A和B的共同部分,所以C的公差一定是两者公差的最小公倍数。
那么我们就可以枚举r的因子(O(sqrtr))作为A的公差p,判断p和q是否最小公倍数为r。
由(1)我们知道a∈[c-r+1,c],共r项,故A的首项有$ \frac r q $个,同理末项也有$ \frac r q $个,累计答案即可。

#include<iostream> #include<cstdio> #include<string> #include<cmath> #include<algorithm> #include<cstring> #include<queue> #include<algorithm> #include<queue> #define N 1000010 #define ll long long using namespace std; ll T; const ll MOD=1e9+7; ll b,c,q,r,y,z; //快读 inline void read(ll &p) { p=0; ll f=1;char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9') p=p*10+(ch-'0'),ch=getchar(); p*=f; } inline bool checkhas() { if(b>c||b+(y-1)*q<c+(z-1)*r||r%q||(c-b)%q) return 0; return 1; } inline bool checkinf() { if(b>c-r||b+(y-1)*q<c+z*r) return 0; return 1; } inline ll finding(ll x) { if(x*q/__gcd(x,q)==r) return (r/x)*(r/x)%MOD; else return 0; } int main() { read(T); while(T--) { ll ans=0; read(b);read(q);read(y); read(c);read(r);read(z); if(!checkhas()) {printf("0\n");continue;} else if(!checkinf()) {printf("-1\n");continue;} else { for(ll i=1;i<=sqrt(r);i++) { if(r%i==0) { ans+=finding(i); ans%=MOD; if(r/i!=i) ans+=finding(r/i); ans%=MOD; } } printf("%lld\n",ans); } } return 0; }
E. Power or XOR?
组合数学+思维
对于一个区间[l,r],我们将区间内的^都看做幂运算,将第l-1个和第r+1个看做异或运算,考察这个区间对总体答案的贡献值。
首先,对于[Al^Al+1,^……^Ar](所有的^表示为幂运算),由于所有的A都是2的幂次,故最终答案在二进制下表示也是10000……000的形式,0的个数为(Bl)Al+1*Al+2*……*Ar 也可表示为2Bl*Al+1*Al+2*……*Ar
其中又有B>=1又A>=2,而答案又要求对22^20取模,故当Bl*Al+1*Al+2*……*Ar>=220==1048576答案贡献必然为0,由于运算具有从左到右的固定先后顺序,可以发现对于每一个起始位置l,我们最多只需要向右枚举20个位置,由于每一个幂次可能会很大造成溢出,我们还要判断当前的幂次是否大于20
然后,我们再来看该区间的贡献,对于一个区间[l,r],我们使用了r-l个幂运算符号以及若干个^符号(当l-1和r+1有值的时候为2,否则为1或者0),我们需要计算该种区间存在于多少不同的表达式E'中,实际上如果这个答案是偶数,那么基于异或的运算的性质贡献依然为0,而奇数的贡献为它本身。
因此这部分的答案为求$(C_m^q+C_m^{q+1}+……+C_m^m) \pmod 2 $ 又有$ C_n^m=C_{n-1}^{m-1}+C_{n-1}^m $.
$(C_m^q+C_m^{q+1}+……+C_m^m) \equiv (C_{m-1}^{q-1}+C_{m-1}^q+C_{m-1}^{q+1}+C_{m-1}^q+……C_m^m) \equiv C(m-1,q-1) \pmod 2 $。该式子可以运用卢卡斯定理求解,直接递归求解会导致超时,由于模数是2,根据卢卡斯定理,当$ ((m-1)|(q-1))==(m-1) $的时候,余数为1,答案有贡献,注意运算符的优先级。
我们枚举每一个区间,求解答案的最终贡献统计答案即可。

#include<cstdio> #include<iostream> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<map> #include<vector> #include<queue> #include<string> #include<bitset> #define N 4001000 #define ll long long using namespace std; //2^20==1048576 ll n,k; ll a[N]; bitset<1048576> bs; //??? inline void read(ll &p) { p=0; ll f=1;char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9') p=p*10+(ch-'0'),ch=getchar(); p*=f; } int main() { read(n);read(k); for(int i=1;i<=n;i++) read(a[i]); for(int l=1;l<=n;l++) { ll lim=1; for(int r=l;r<=n;r++) { if(r==l) lim=a[l]; else if(a[r]>=20) break; else lim*=(1ll<<a[r]); if(lim>=1048576) break; ll m=n-(r-l+1)-2; ll q=k-2; if(l==1) {m++;q++;} if(r==n) {m++;q++;} if(m>=q && (m==0||(((m-1)|(q-1))==(m-1)&&q>0))) bs[lim]=bs[lim]^1; } } bool f=0; for(int i=1048575;i>=0;i--) { if(bs[i]==0&&f) printf("0"); else if(bs[i]==1) { printf("1"); f=1; } } if(!f) printf("0"); printf("\n"); return 0; }
F. Anti-Theft Road Planning
我们建立的路径一定要可追踪,假设我们将所有的城市打上序号,将路径长设置为两城市的序号的异或,那么最终贼的路径一定是起点序号异或终点序号,但是如果我们直接按顺序标记的话,最后路径的长度会超过48000。
我们可以想到一种相邻序号之间只有一位不同的标记方法---格雷码,格雷码有两种常见的构造方法:
1.翻转最低位得到一个再将最低位的1的左侧翻转得到下一个不停的循环得到所有的格雷码
2.当我们知道前2n-1个格雷码,我们可以从最后到第一个复制一遍接在数组后面(相当于镜像复制一遍),然后复制前的数组前面加上0,新加上的位置数组前面加上1,产生2n个格雷码。
我们现在考虑将格雷码拓展为二维的形式,由于和每个数字相邻的数字有四个方向,所以我们一个数字要和四个数字都产生一位不同。
1.对于第一种转换方式,那么在同一行方向上,我们改为翻转倒数第二位,然后翻转左侧两位,在同一列方向上,我们翻转最后一位,然后翻转左侧两位。
2.对于第二种方式,我们按照镜像以y轴为对称轴翻转,然后在以x轴为对称轴翻转,然后左上角前面为00,右上角设置为10,左下角设置为01,右下角设置为11.
这两种的构造都是一样的。
n=23的结果:
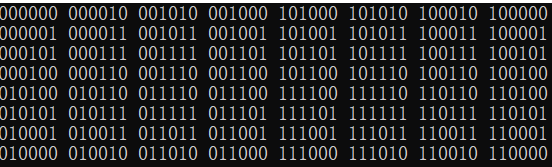
我们来证明这种方式符合题意:
以第二种产生方式为例,在两个对称轴两侧的序号,相邻的数字之间异或是新产生的数字,其他的道路是原本的4倍,假设以此产生了n=2m的矩阵。
增量为2m*2m-1+2m*2m-2=2m*4m-1*3
和前m-1项累加有 2m*4m-1*3+(2m-1*4m-2*3)*4+(2m-2*4m-3*3)*4……+2*1*3*4m-1=(2+4+……+2m)*3*4m-1=4m*$ \frac 3 2 $*(2m-1)。
当m=5时,路径和为47616,小于48000,符合答案。
由于横向的路径只有偶数位有效,纵向只有奇数位有效,因此很好得出答案。

#include<iostream> #include<cstdio> #include<string> #include<algorithm> #include<cstring> #include<cmath> #include<queue> #include<ctime> #define N 35 #define ll long long using namespace std; int dh[N]={1, 4, 1, 16, 1, 4, 1, 64, 1, 4, 1, 16, 1, 4, 1, 256, 1, 4, 1, 16, 1, 4, 1, 64, 1, 4, 1, 16, 1, 4, 1}; //int dlie[N]={} int n,k; int pre[N]; const int MOD=341; //快读 inline void read(ll &p) { p=0;ll f=1; char ch=getchar(); while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9') p=p*10+(ch-'0'),ch=getchar(); p*=f; } inline void doing() { for(int i=0;i<=30;i++) pre[i+1]=pre[i]^dh[i]; for(int i=0;i<n;i++) { for(int j=0;j<n-1;j++) { if(j!=n-2) cout<<2*dh[j]<<" "; else cout<<2*dh[j]; } cout<<endl; } for(int i=0;i<n-1;i++) { for(int j=0;j<n;j++) { if(j!=n-1) cout<<dh[i]<<" "; else cout<<dh[i]; } cout<<endl; } cout<<flush; } int main() { cin>>n>>k; doing(); int x=0,y=0; while(k--) { int v; cin>>v; for(int i=0;i<32;i++) { if((pre[x]^pre[i])==(v&MOD)) { x=i; break; } } for(int i=0;i<32;i++) { if((pre[y]^pre[i])==((v>>1) & MOD)) { y=i; break; } } cout<<x+1<<" "<<y+1<<endl; } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号