区块链第一章
区块链1
1. 有限域
- 如果a和b属于集合,则a+b和a·b也属于集合。我们称此性质为封闭性。
- 存在0使得a+0=a。我们称此性质为加法恒等。
- 存在1使得a·1=a。我们称此性质为乘法恒等。
- 如果a属于集合,则-a属于集合;满足a+(-a)=0。我们称此性质为加法逆。
- 如果a属于集合,则a-1属于集合,满足a·a-1=1。我们称此性质为乘法逆。
Fp={0,1,2,3,...,p-1},集合元素大小(阶)是p
域的阶数必须为质数的整数次幂
负数也可以进行模运算,-27%13=12,-3%15=12
我们使用+f符号来代表有限域的加法,以免和常用的整数加法(+)混淆。
F19={0,1,2,...,18}
加法封闭意味着:a+fb∈F19我们使用+f符号来代表有限域的加法,
以免和常用的整数加法(+)混淆。
a+fb=(a+b)%19
例如:7+f8=(7+8)%19=15
11+f17=(11+17)%19=9
有限域减法:
a-fb=(a-b)%p(a,b∈Fp)
乘法:
8·f17=8+f8+f8+...+f8(共计17个8)=(8·17)%19=136%19=3
费马小定理
当p为质数时,n(p-1)%p=1。a的p-1次幂得1
除法:
在F19中:2/7=2·7(19-2)=2·717=465261027974414%19=3
7/5=7·5(19-2)=7·517=5340576171875%19=9
2. 第一章Fieldelement的实例化操作及练习题
class Fieldelement:
def __init__(self,num,prime):
if num >= prime or num < 0:
error='num {} is not in the range from 0 to {}'.format(num,prime-1)
raise ValueError(error)
self.num=num
self.prime=prime
def __repr__(self):
return 'Fieldelement_{}({})'.format(self.prime,self.num)
def __eq__(self, other):
if other is None:
return False
return self.num==other.num and self.prime==other.prime
def __ne__(self,other):
if other is None:
return True
return self.num!=other.num or self.prime!=other.prime
def __add__(self,other):
if self.prime!=other.prime:
raise TypeError('two primes must be the same')
num=(self.num+other.num)%self.prime
return self.__class__(num,self.prime)
def __sub__(self, other):
if self.prime!=other.prime:
raise TypeError('two primes must be the same')
num=(self.num-other.num)%self.prime
return self.__class__(num,self.prime)
def __mul__(self, other):
if self.prime!=other.prime:
raise TypeError('two primes must be the same')
num=(self.num*other.num)%self.prime
return self.__class__(num,self.prime)
def __pow__(self, power):
if power>=0:
result = (self.num ** power) % self.prime
return self.__class__(result, self.prime)
elif power<0:
while power<0:
power+=self.prime-1
num=(self.num**power)%self.prime
return self.__class__(num,self.prime)
def __truediv__(self, other):
if self.prime!=other.prime:
raise TypeError('two primes must be the same')
num=(self.num*(other.num**(self.prime-2)))%self.prime
return self.__class__(num,self.prime)
3.所有域加减乘除幂运算都是在prime(p)相等条件下进行
a=Fieldelement(3,18)
b=Fieldelement(5,18)
print(a**-3)
print(a+b)
同样可以进行相等或不相等比较
print(a!=b)
print(a==b)
4.自己对第一章的理解
- 域就相当于一个时钟,或者说是最大值+1进制的运算操作
- 本章中class类别下所定义的函数都是在实例化后自动执行的,因为函数两边带有两个_
以下是代码调试图片
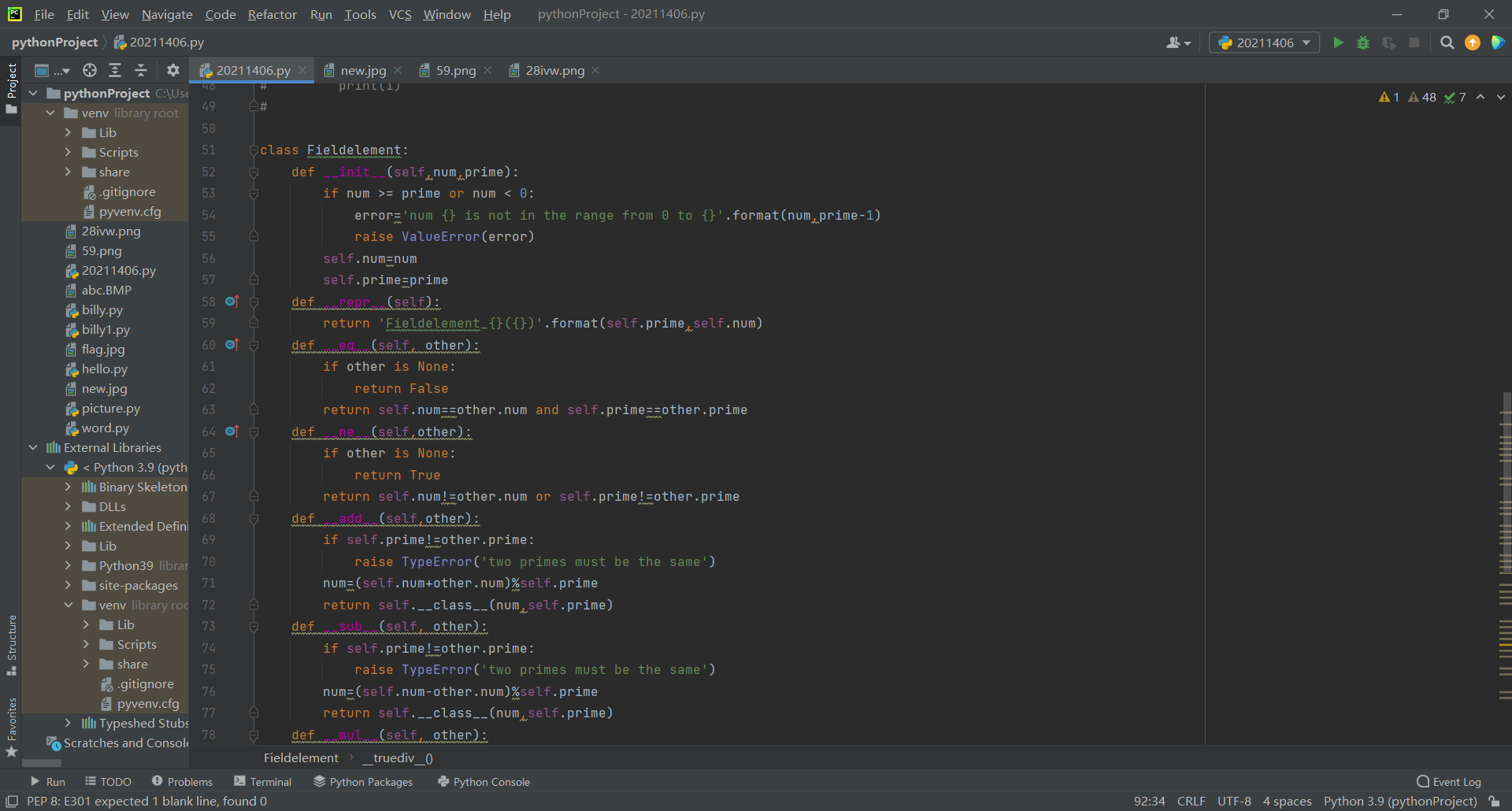
posted on 2021-11-10 20:33 20211406张顺扬 阅读(98) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号