wqs二分

wqs二分

本来是想写到杂项里的，但是觉得这个东西真的好牛逼，予以尊重，放到这里。

简介

wqs 二分是王钦石提出的一类二分方式。

基本是用来处理一类带有限制的问题的。比较明显的标志就是“恰好选 \(k\) 个”。

使用 wqs二分有一个前提，就是原问题必须具有凹凸性。

具体处理

比方说我们设 \(f_i\) 表示选 \(i\) 个物品的最优方案，那么把 \((i,f_i)\) 扔到坐标系上，一定要是一个凸包。我们的目标在于求出 \(f_m\)。

我们考虑二分一个斜率 \(k\)，然后需要找到斜率为 \(k\) 的直线会切于这个凸包的哪一个点。可以发现，随着 \(k\) 的减小，这条直线的切点会越来越靠右。扒一张网图：

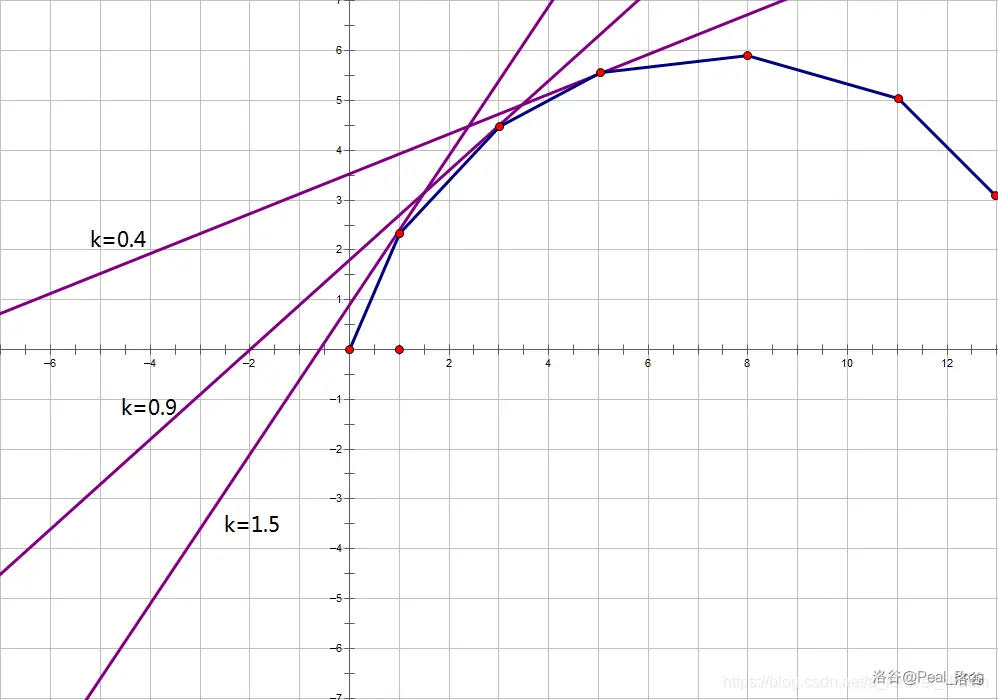
那么我们就需要二分 \(k\) 直到这条直线切的点的横坐标为 \(m\)，那么这个点的纵坐标 \(f_m\) 即为所求答案。

现在原问题变成了：当有一个斜率 \(k\)，凸包上被切的点是谁。

这边再贴一张网图：

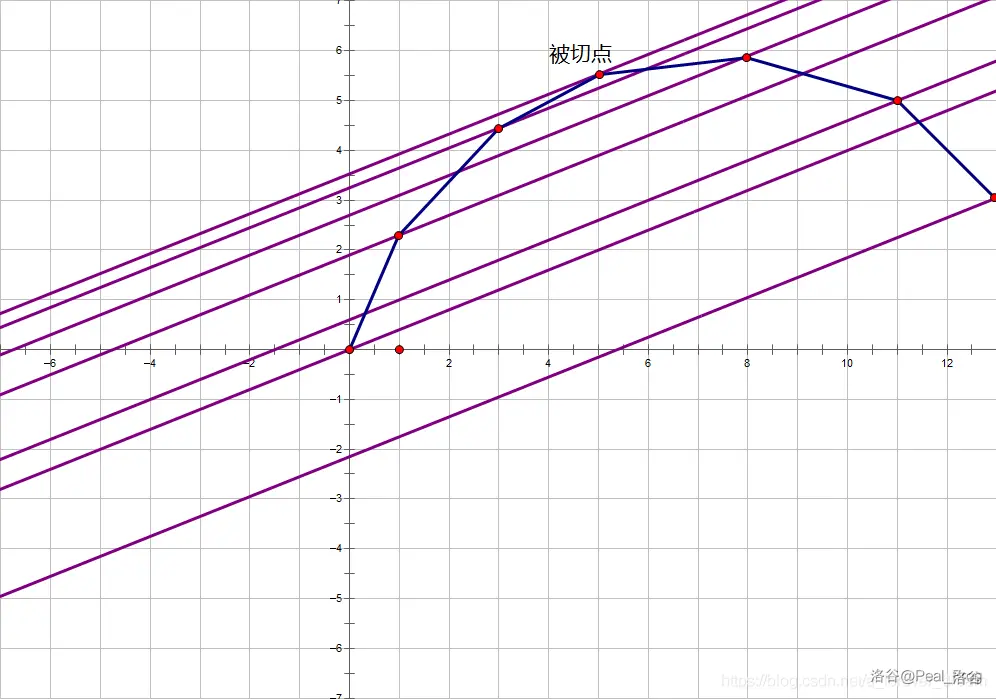
我们发现，对于这个凸包而言，被切点是 \(y\) 轴截距最大的点。

我们把这条直线写下来就是 \(y=kx+b\)，那么这个截距就是 \(b\)，且 \(b=-kx+y\)。对于每个点而言，设一个 \(g_x\)，且 \(g_x=-kx+f_x\)，则 \(g_x\) 最大的点即为切点。

相当于就是你每选一个物品，你的代价就会额外加一个 \(-k\)，\(g_x\) 就可以表示这个 \(f_x\) 所选物品的数量。那么，当你这个 \(f_n\) 取到最优方案即最大值时，你这个 \(g_n\) 即为直线所切的点的横坐标。

这后面这一坨纯粹是我自己的理解，所以可能思路比较混乱。我试图呈现出来我自己理解的全过程。

相关题目

这个不能叫例题，只能说我觉得很好的一道题。

P9338 [JOIST 2023] 合唱 / Chorus

我是通过这道题了解 wqs二分的，后面做完也不是很懂，后来看了 msb 的课件又自己做了几道题算是更懂了很多。

#include <bits/stdc++.h>
#define int long long
#define il inline

using namespace std;

const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 2e6 + 10;
int n, kk, a[N];
char ss[N];
int c[N], p[N], s[N];
int f[N], g[N]; 
int mid;
il int y(int j) {return -f[j] + s[p[j] - 1] - j * p[j] + j;}
il int k(int i) {return i;}
il int x(int j) {return -j;}
il int b(int i) {return -f[i] - mid + s[i];}
il double slope(int i, int j) {
	return 1.0 * (y(i) - y(j)) / (x(i) - x(j));
}
int q[N], head, tail;
vector<int> num[N];
il bool check(int mm) {
	mid = mm;
	for (int i = 1; i <= n; i++) f[i] = g[i] = INF;
	head = 1, tail = 0;
	for (int i = 1; i <= n; i++) {
		for (int j : num[i]) {
			while (head < tail && slope(q[tail - 1], q[tail]) > slope(q[tail], j)) tail--;
			q[++tail] = j;
		}
		while (head < tail && slope(q[head], q[head + 1]) < k(i)) head++;
		f[i] = -mid + s[i] - y(q[head]) + k(i) * x(q[head]);
		g[i] = g[q[head]] + 1;
	}
	return g[n] <= kk;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n >> kk >> ss;
	for (int i = 1; i <= 2 * n; i++) a[i] = (ss[i - 1] == 'A');
	int cnt = 0, tot = 0;
	for (int i = 1; i <= 2 * n; i++) {
		if (a[i] == 1) c[++tot] = cnt;
		else cnt++;
	}
	for (int i = 0; i <= n; i++) {
		p[i] = lower_bound(c + 1, c + 1 + n, i) - c;
		p[i] = max(p[i], i + 1);
		num[p[i]].push_back(i);
	}
	for (int i = 1; i <= n; i++) {
		s[i] = s[i - 1] + c[i];
	}
	int L = -INF, R = 0, ans = 0;
	while (L <= R) {
		mid = (L + R) / 2;
		if (check(mid)) {
			ans = mid;
			L = mid + 1;
		} else {
			R = mid - 1;
		}
	}
	check(ans);
	cout << f[n] + kk * ans << "\n";
	
	return 0;
}