机器学习—单变量线性回归

本篇讲述以下内容：

单变量线性回归
代价函数
梯度下降

单变量线性回归

回顾上节，在回归问题中，我们给定输入变量，试图映射到连续预期结果函数上从而得到输出。单变量线性回归就是从一个输入值预测一个输出值。输入/输出的对应关系就是一个线性函数。

下面是一个根据房屋面积预测房屋价格的例子。

假设有一个数据集，我们称作训练集，数据集包括房屋面积和房屋价格数据。

x：表示输入变量，也叫特征变量。

y：表示输出变量，也叫目标变量。

(xⁱ,yⁱ)：表示一个识训练样本，训练集的一行。i 表示第 i 个训练样本。

m：表示训练样本的数量。

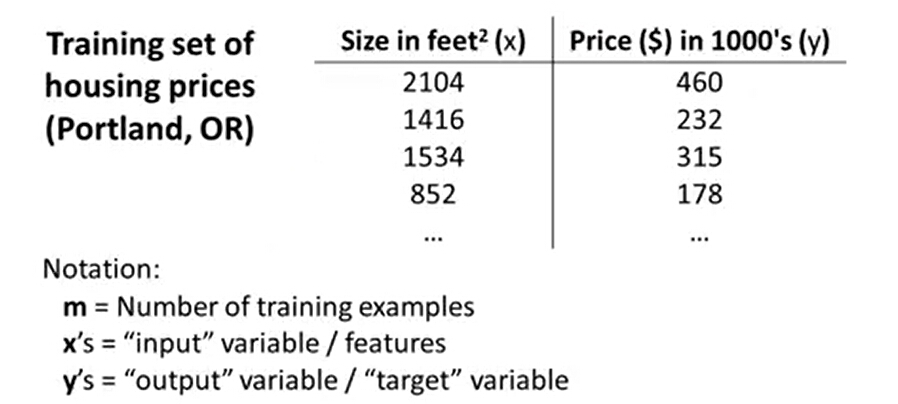
在接下来的学习之前，先了解一下监督学习的一般工作方式。如下图，训练集通过学习算法训练后，得到一个h(hypothesis)，它表示为一个函数。

函数的输入为房屋大小，输出为房屋的价格。通过这个函数我们则可以预测房屋价格，这就是机器学习中的回归问题。

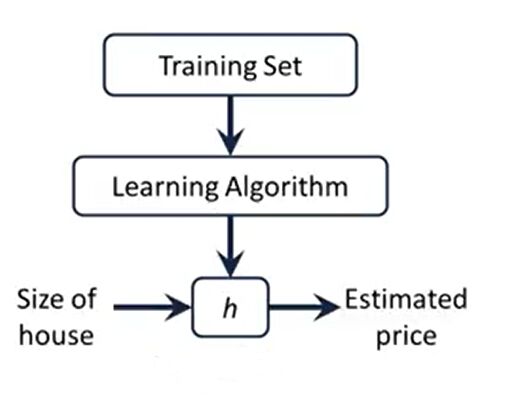
在单变量线性回归中，我们的假设函数为： $h θ (x)=θ 0 +θ 1 x ，其中 θ 0 和θ 1 为模型参数。$

$讲到这肯定有疑惑为什么要选这个函数，实际应用可能不是线性的函数，可能会是更复杂的函数。这里只是为了从简单线性方程的例子入手，假设房屋的面积和价格是一个线性关系。$

好继续，我们有了假设函数，接下来要做的就是如何选择不同的参数 $θ 0 和θ 1$ 。下图可以看到不同的参数值会得到不同的假设函数。

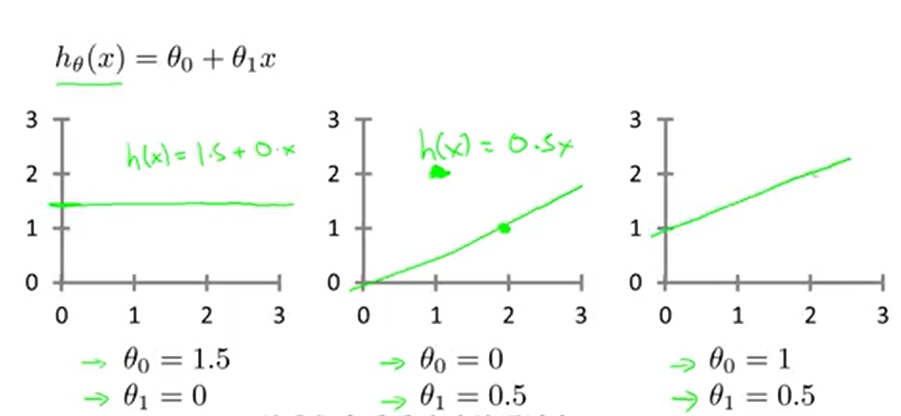
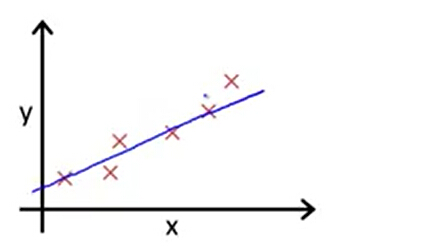
我们选择参数 $θ 0 和θ 1$ 得到的直线，应该尽量和训练数据拟合。这样才能做出比较精准的预测。

那么如何来使它来更好的拟合数据呢？我们的想法是 $h θ (x)$ 应该最接近 y 值，即问题转化成了一个mininize( $h θ (x)$ -y) 的问题，有没有感觉转化成数学问题了。

代价函数

接下来引入一个代价函数Cost Function，也被称作平方误差函数。

函数定义如下，每个训练样本 $h θ (x)-y 的平方和，再求平均。再乘1/2是为了接下来的计算上的方便。$

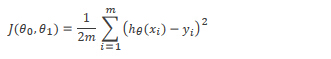
我们想要做的就是关于 $θ 0 和θ 1$ 对函数J( $θ 0 ，θ 1$ )求最小值。即找到使得J( $θ 0 ，θ 1)$ 最小值的时候， $θ 0 和θ 1 的值。接下来介绍一种算法，梯度下降。它能自动的找出使 J 最小化的参数 θ 0 和θ 1 的值。$

梯度下降

了解梯度下降前，我们了解一下J( $θ 0 ，θ 1)$ 的函数图像。

当 $θ 0$ 为0时，随着的变化 $θ 1$ 将会得到下图的效果。 $θ 1$ 取1的时候 J 为最小值

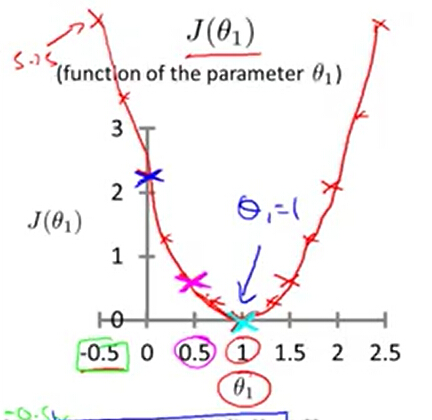
当 $θ 0 和θ 1$ 都有值时。

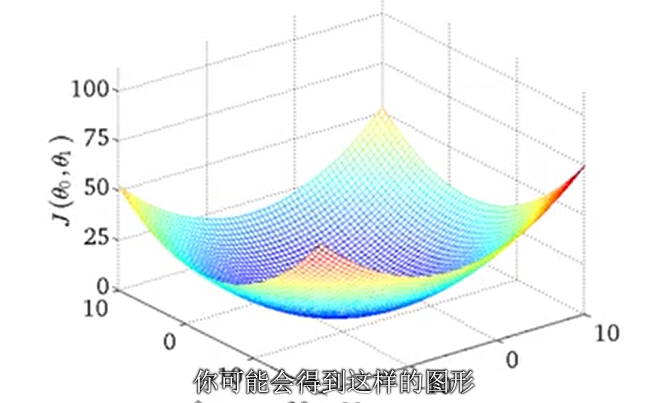
好了，回到我们之前问题描述，我们有一个代价函数J( $θ 0 ，θ 1)$ ，想通过一个算法来使用得 J 最小化。

那么梯度下降的思想就是：

开始给定一个（ $θ 0 ，θ 1$ ）初始值，我们想通过不断的改变 $θ 0 ，θ 1$ 的值，每次改都使得 J 减少。最终J 减少到最小。

下面通过图我们来看梯度下降是如何工作的。

首先想象一下，对 $θ 0 ，θ 1$ 赋以某个初始值（一般可以初始化为0）。假设初始化后，J 对应是下图的标红的这个点。

我们想象这是一座山，你站在山上的这个点上。在梯度下降中，我们要做的是看看周周围，并问自己我想要通过小碎步下山，朝哪个方向能最快下山？并朝着这个方向前行。

每走一步都需要调整最快的那个方向。最终你走出了这么一条轨迹。最终走到一个局部最优解——山脚下。当然如果你是站在另一个点，你可以会走出另一条轨迹。

上面是通过图直观的感受，那么事实上在这走一步的方向，其实就是梯度的负方向。梯度其实就是J的导数，对于一个线性函数，也就是线的斜率。

如果把每一步的长度定义为学习速率。那么每走一步的这个动作，其实就是 $θ 0 ，θ 1$ 都朝梯度的负方向进行更新。控制着更新的幅度。

下图是数学定义：即按照一定的学习速率，不断重复更新 $θ 0 ，θ 1$ 直到 J 局部收敛到最小值。

下图是对一元线性函数的直客感受，如下图函数上的某点，沿红色方向，即斜率的反方向下降一个步长到另一点。 $θ 1$ 将得到 -* 斜率的更新。

另一个方向也是同样效果。

其中关于学习速率大小的的选择对算法的影响，如果速率太小，则下降的速度比较慢。如果速率过大，会无法收敛到最小值。

如果 $θ 1$ 的选择一开始就是最优点。那么这个点的导数为0， $θ 1$ 则不会得到更新。

梯度下降的过程中，导数的值会不断变小，下降的幅度也会自然的减少。所有没有必要在下降的过程中调整学习速率。

在线性回归中，梯度下降的具体实现

前面讲了梯度下降的数学特性，那么在线性回归的训练算法中是如何应用的呢。

下图左边是梯度下降的算法，右边是线性回归的模型。

要实现这个算法，我们还差这个关键项。它表示分别对 $θ 0 ，θ 1$ 求导，可以参数数学上的求导方法。

对 $θ 0$ 求导后得到

对 $θ 1 求导后得到$

然后代到梯度下降的公式中。每一次循环，都要分别求出 $θ 0 ，θ 1$ 的更新值然后更新。

课后练习代码，Octave实现。

现在有一家餐饮连锁公司，关于城市人口和利润的数据。我们要得到城市人口和利润的预测函数。

先用可视化的方式Plot 这些数据。

%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples

% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);

fprintf('Program paused. Press enter to continue.\n');
pause;

function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure 
%   PLOTDATA(x,y) plots the data points and gives the figure axes labels of
%   population and profit.

% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the 
%               "figure" and "plot" commands. Set the axes labels using
%               the "xlabel" and "ylabel" commands. Assume the 
%               population and revenue data have been passed in
%               as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
%       appear as red crosses. Furthermore, you can make the
%       markers larger by using plot(..., 'rx', 'MarkerSize', 10);

figure; % open a new figure window

plot(x, y, 'rx','MarkerSize',10); %Plot the data

ylabel('Profit in $10,000s'); %Set the y-axis lable

xlabel('Population of City in 10,000s'); %Set the x-axis lable

% ============================================================

end

用梯度下降方法，得到一个最佳似合直线。

%% =================== Part 3: Gradient descent ===================
fprintf('Running Gradient Descent ...\n')

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters

% Some gradient descent settings
iterations = 1500; %定义循环次数
alpha = 0.01; %定义学习速率

% compute and display initial cost
computeCost(X, y, theta)

% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);

CostFunction 代价函数实现，

function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.

temp = (X * theta) - y ;

J = (1 / (2 * m)) * sum( (temp.^2) ) ; 

% 矩阵运算方式

% temp'*temp

% =========================================================================

end

梯度下降实现

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %

temp1 = theta(1) - (alpha / m) * sum((X * theta - y ).*X(:,1));

temp2 = theta(2) - (alpha / m) * sum((X * theta - y).* X(:,2));  

theta(1) = temp1;

theta(2) = temp2;

% 矩阵运算方式
% theta = theta - alpha * (X' * (X * theta - y)) / m;  
    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end

end

打印结果

% print theta to screen
fprintf('Theta found by gradient descent: ');
fprintf('%f %f \n', theta(1), theta(2));

% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure

% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
    predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
    predict2*10000);

fprintf('Program paused. Press enter to continue.\n');
pause;

注：上述学习资料参考：https://www.coursera.org/learn/machine-learning

posted on 2015-11-20 15:17 张日海阅读(3667) 评论(0) 编辑收藏举报

刷新页面返回顶部

海的天空