固体激光器聚光腔的设计

目录

• 固体激光器聚光腔的设计
  • 聚光腔的作用
  • 聚光腔的分类
    • 椭圆聚光腔
    • 漫反射聚光腔
  • 能量转换特性
    • 理论耦合效率
    • 泵浦源发射的光线轨迹
  • 几何传输效率
    • 几点假设
    • 灯通过椭圆上的任一点在棒端成像
  • 几何传输系数 \(\eta _{ge}\) 求解
  • \(P_0\) 点的确定
  • 灯的遮挡
  • 习题
  • 漫反射腔的效率
  • 泵浦光在激光棒内分布
    • 均匀光场中棒内光能的分布
    • 椭圆柱聚光腔的泵浦光分布
  • 聚光腔的设计
    • 步骤
    • 聚光腔常用材料的反射率

---

固体激光器聚光腔的设计

聚光腔的作用

从泵浦光源发出的辐射能传输到激光工作物质上的效率，在很大程度上决定了激光系统的总效率，

1. 给泵浦光源和工作物质之间提供良好耦合
2. 激光物质上泵浦光密度的分布，从而影响到输出光束的均匀性、发散度和光学畸变。

由于激光工作物质和泵浦灯都安装在聚光腔内，合理设计聚光腔是决定固体激光器工作性能的重要条件之一。但并不是所有的固体激光器都需要聚光腔。

聚光腔的分类

聚光腔的分类主要依据: 聚光腔的结构 和 功能。

椭圆聚光腔

高反射率椭圆柱体，激光棒和泵浦灯分别配置在椭圆柱的两条焦线上。由椭圆的一个焦点发出的光将反射到另一个焦点。因此，椭圆腔中的能量传递，是从一条焦线上的直管光源传输到另一条焦线上的棒状吸收体。

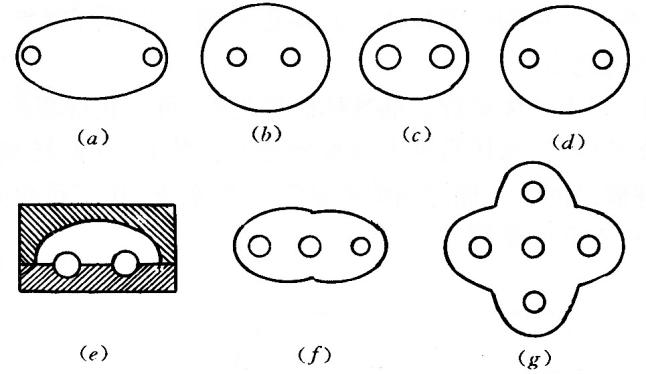
漫反射聚光腔

最简单的聚光腔是一种陶瓷圆柱体。其中激光棒和泵浦灯紧靠在一起。陶瓷材料具有不会腐蚀或生锈的优点。

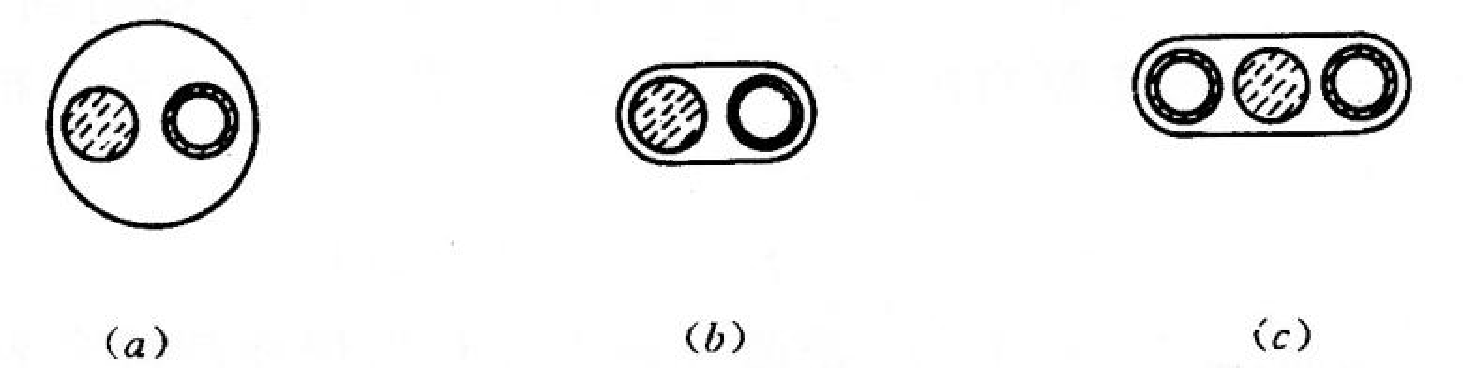
能量转换特性

理论耦合效率

\[\eta =\eta _{ge} \cdot \eta _{op} \]

\(η_{ge}\) 是聚光腔的几何传递系数，它是计算泵浦灯发出的光直接射到和由腔壁反射到激光棒上的百分比；

\(η_{op}\) 是聚光腔的光学效率，基本上反映了系统中全部损耗的影响大小，其表达式可以表示为下式

\[\eta _{op}=\gamma _{\omega}(1-\gamma _r)(1-a)(1-f) \]

其中，\(\gamma _{\omega}\) 是腔壁对泵浦光的反射率； \(\gamma _r\) 是激光棒表面和玻璃冷却液套表面的反射损耗，以及在腔内插入的任何滤光片的菲涅耳损耗；\(a\) 是灯和激光棒之间的光学介质（如冷却液、滤光片等）中的吸收损耗；\(f\) 为腔的非反射面积与总的内表面积之比

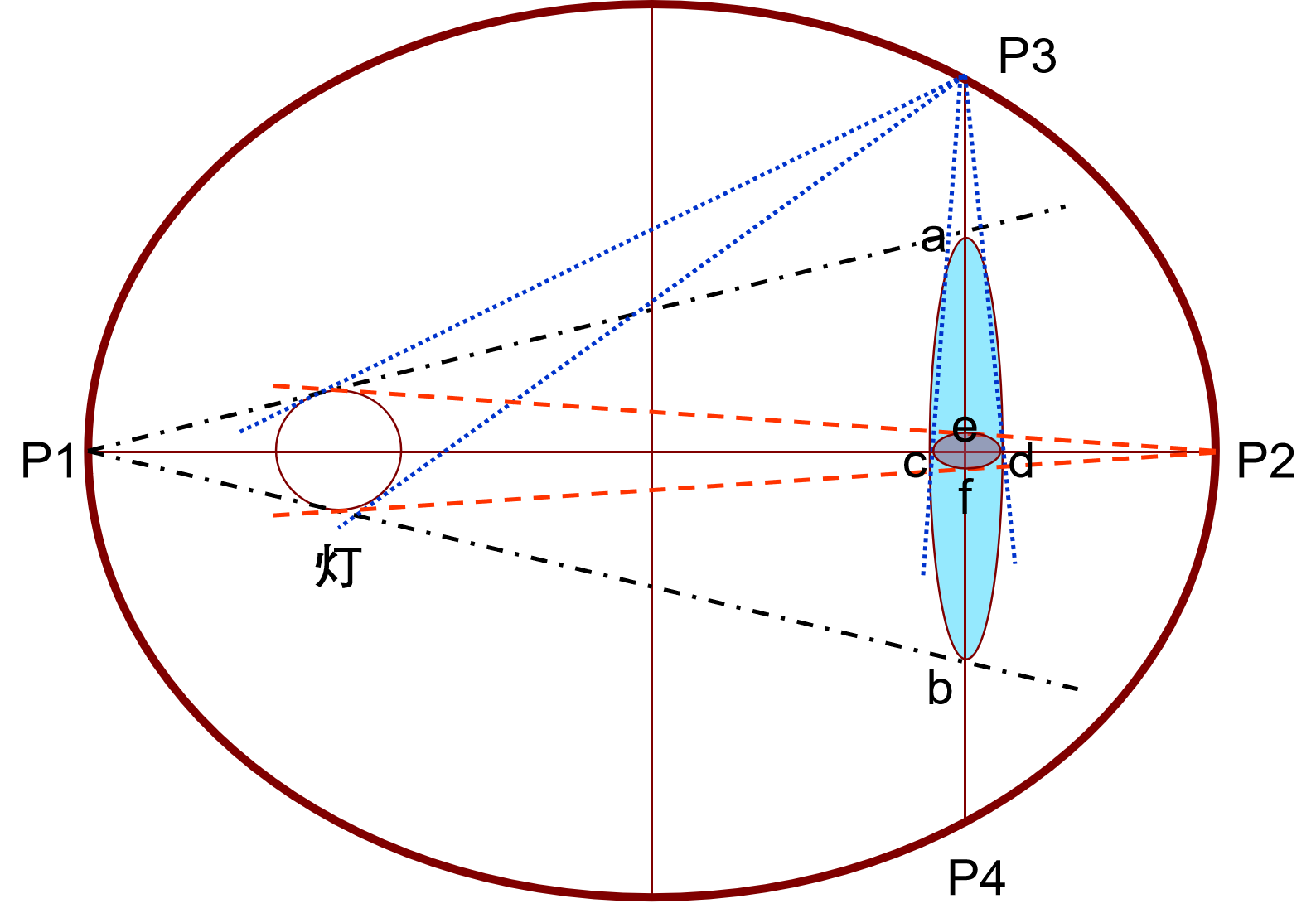
泵浦源发射的光线轨迹

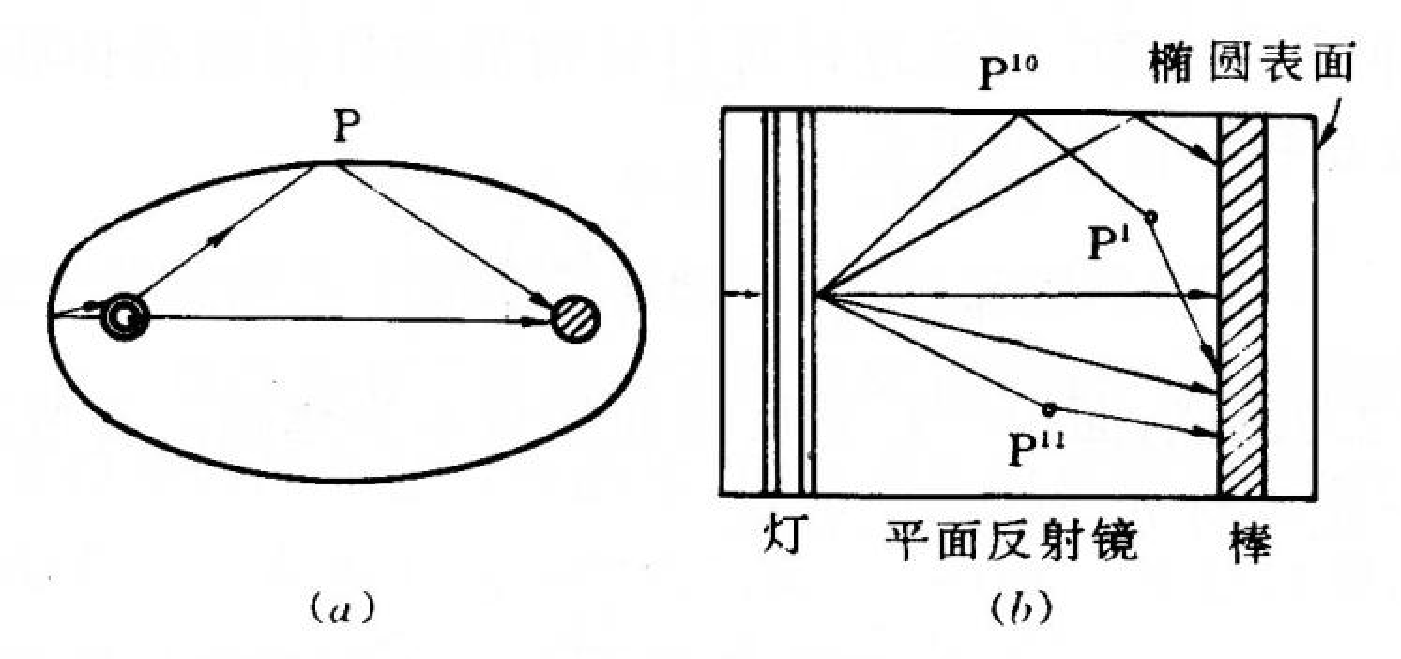
几何传输效率

几点假设

1. 灯在圆截面上对称均匀发光
2. 不考虑轴向倾斜光线
3. 只考虑一次反射光线，焦点上泵浦
4. 不考虑直接照射，遮挡，忽略反射损耗
5. 灯作为黑体对待

聚光腔各部分的几何参数

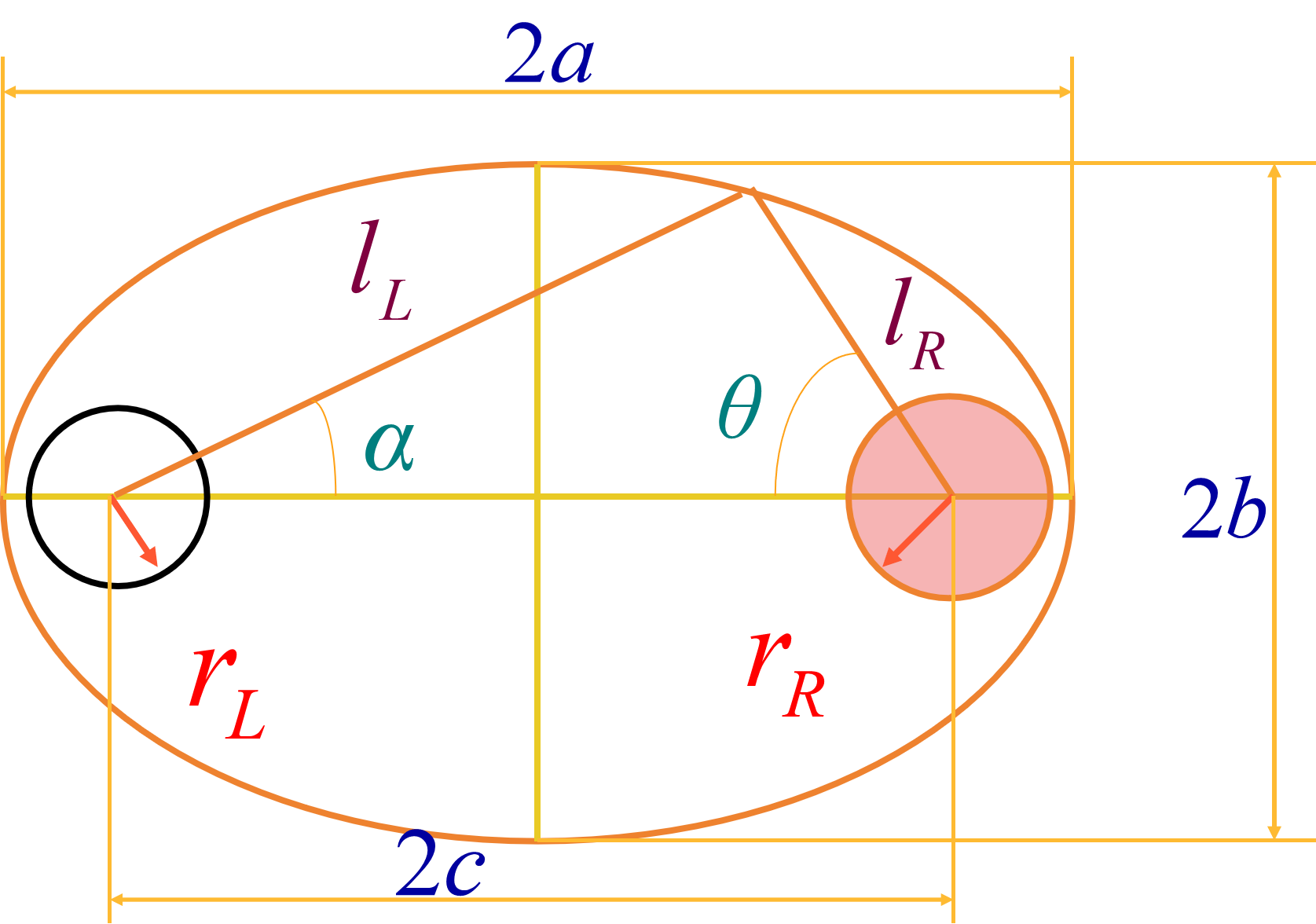
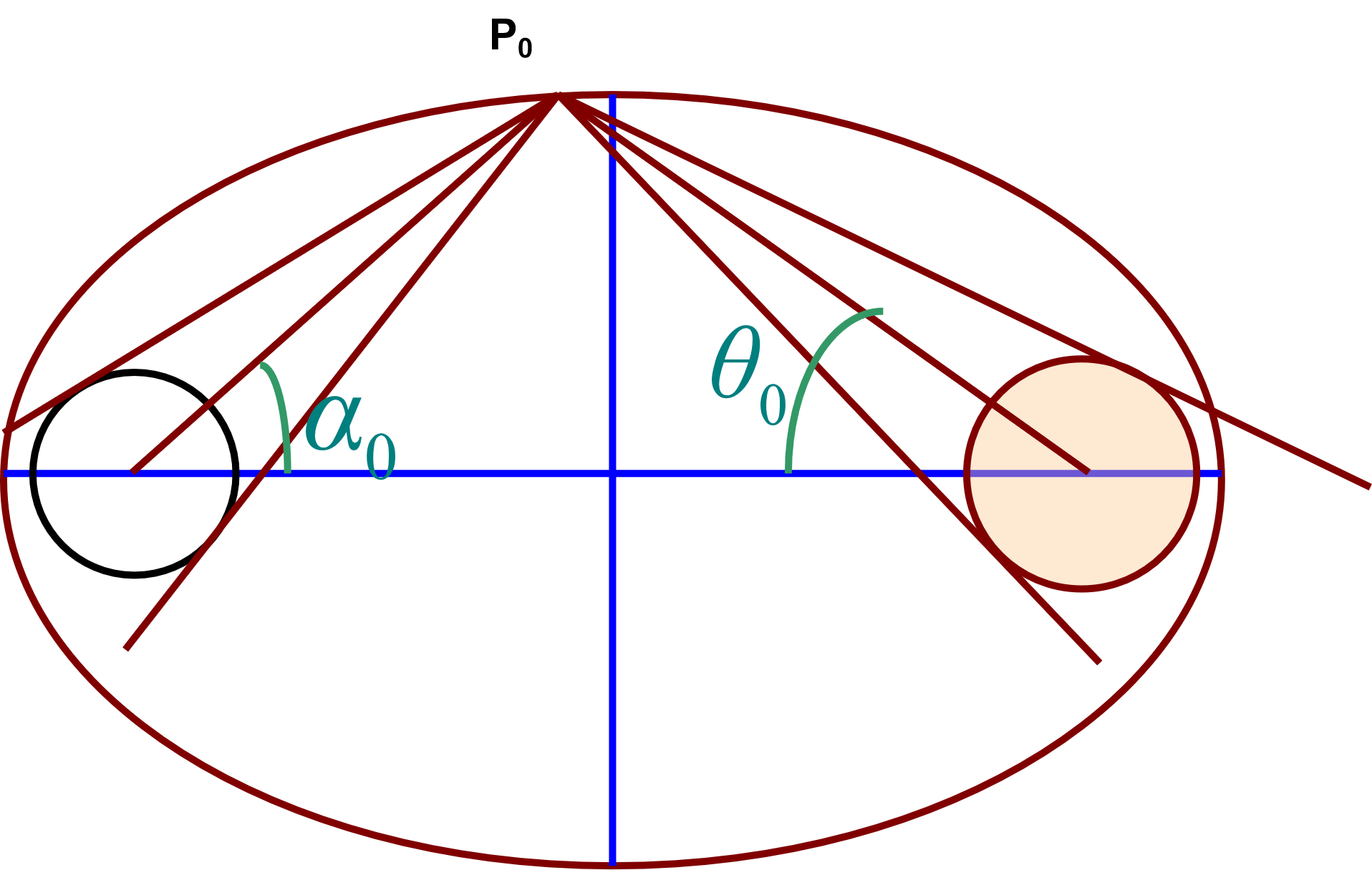
灯通过椭圆上的任一点在棒端成像

\[r_L^{\prime}= r_L(\frac{l_R}{l_L}) \]

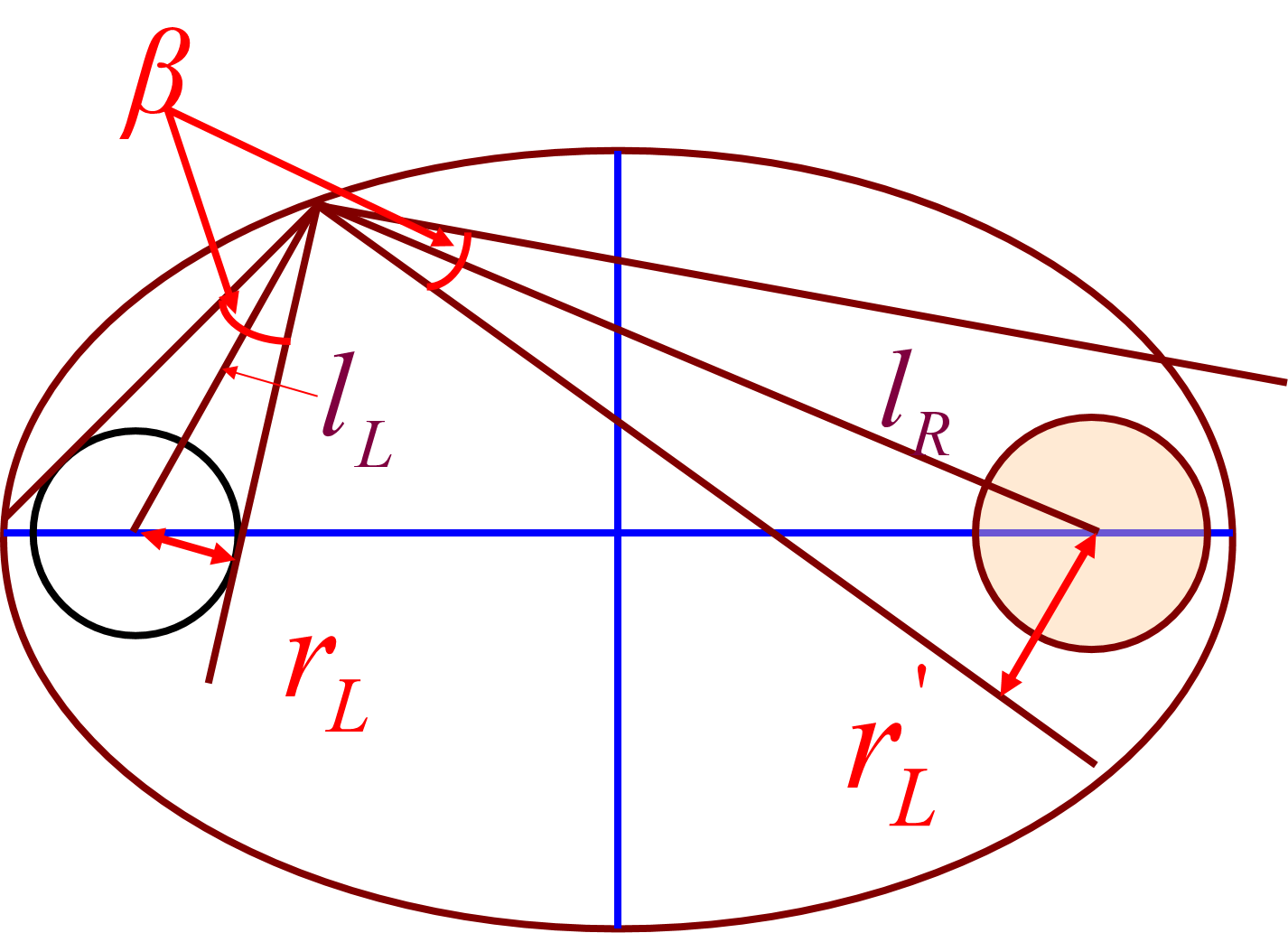
• \(r_L^{\prime}=r_R\), \(P_0\) 点灯像半径等于棒半径

  

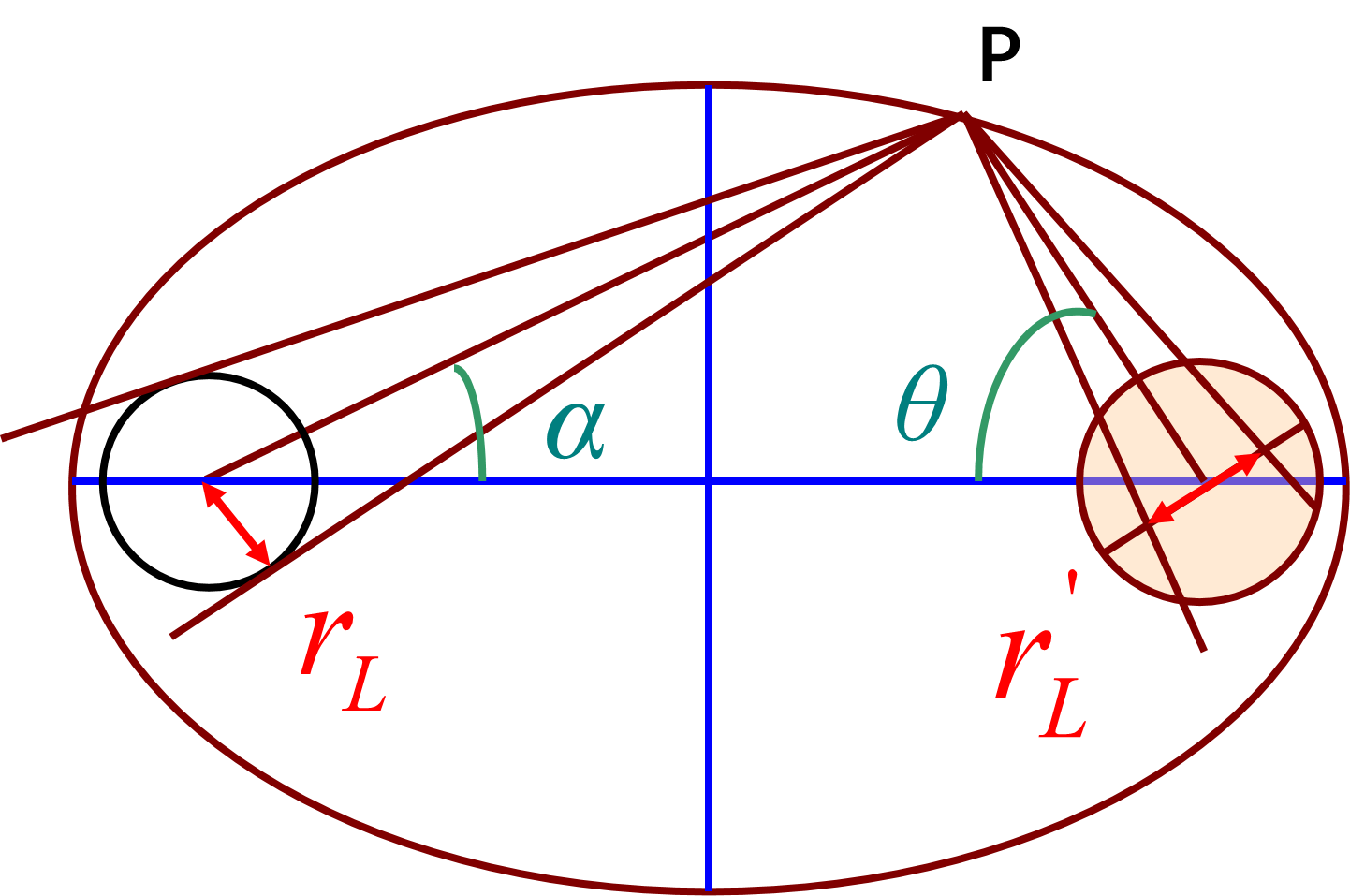
• \(0<\alpha<\alpha_0\Longrightarrow r_L^{\prime}<r_R\Longrightarrow\eta_p=1\)

  

  \(\eta_p\) 为棒接收经 P 点反射光能的比例

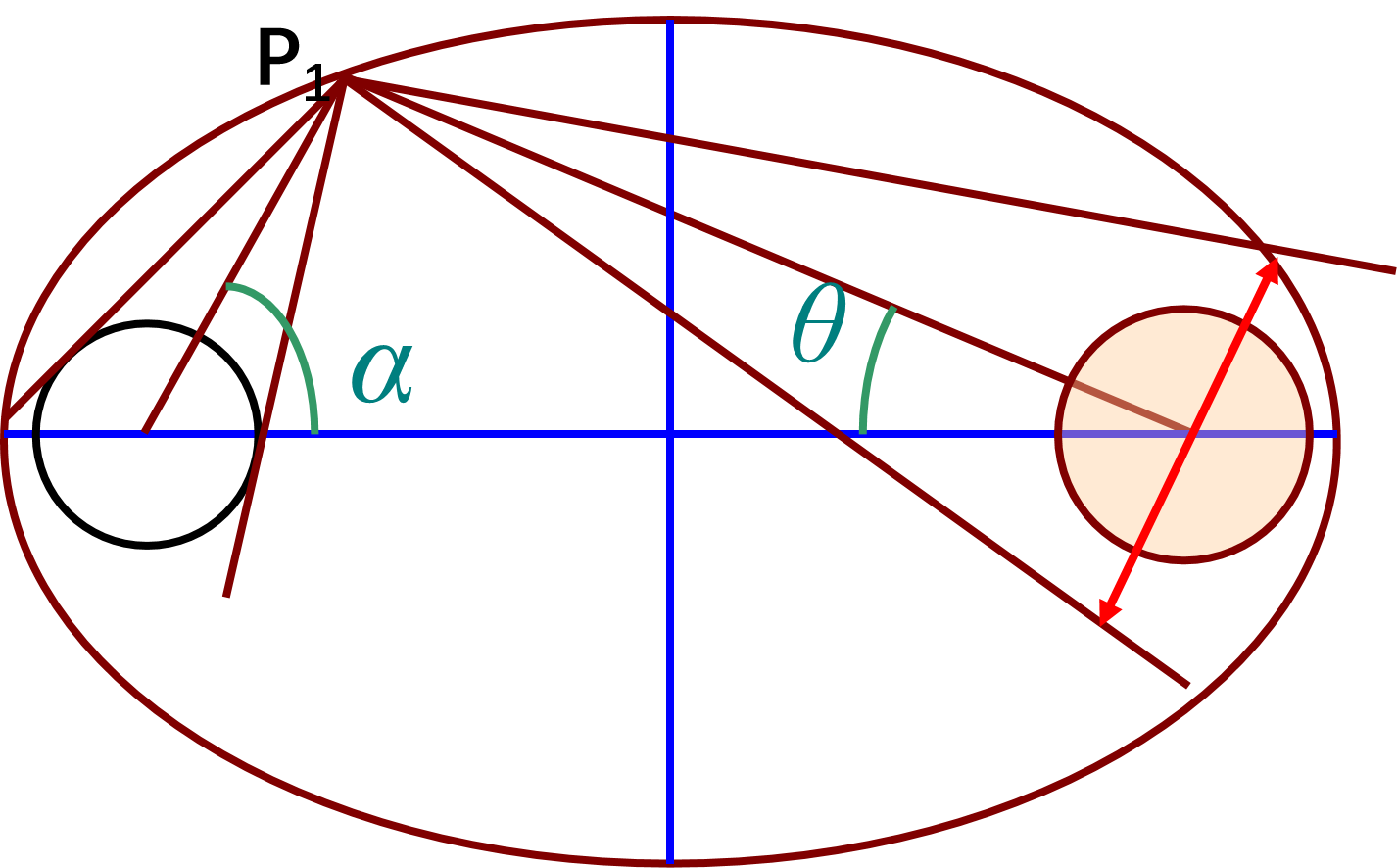
• \(\alpha > \alpha_0 \Longrightarrow r_L^{^{\prime}} > r_R \Longrightarrow \eta_p =\frac{r_R}{r_L^{^{\prime}}}= \frac{r_R}{r_{L}}\cdot \frac{l_L}{l_R}<1\)

  

几何传输系数 \(\eta _{ge}\) 求解

聚光腔的几何传输系数 \(\eta _{ge}\)，可通过计算灯辐射能在灯转给晶体张角 \(d_{\alpha}\) 内的那部分能量得到，对所有张角积分便导出公式[\(\ref{eq4}\)]

\[\begin{aligned} \eta _{ge}&=\frac{1}{E}\int_0^{2\pi}{(\frac{E}{2\pi})\eta _pd\alpha} \\ &=\frac{1}{\pi}[\int_0^{\alpha _0}{\eta _pd\alpha}+\int_{\alpha _0}^{\pi}{\eta _pd\alpha ]} \\ &=\frac{1}{\pi}[\alpha _0+\int_{\alpha _0}^{\pi}{\frac{r_R}{r_L}\frac{l_L}{l_R}d\alpha ]} \end{aligned} \]

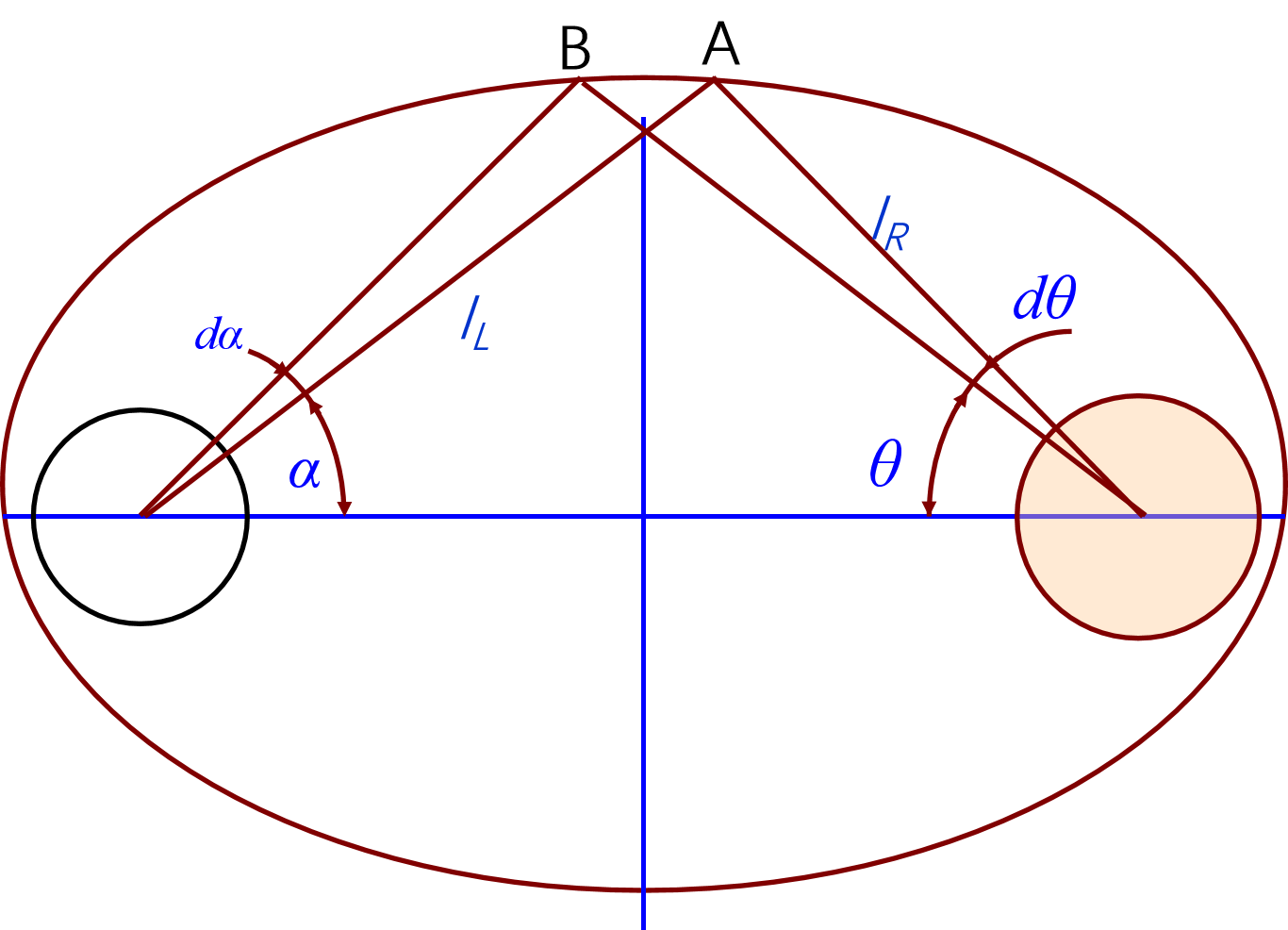
其中，\(\alpha_0和\frac{l_L}{l_R}\) 代求，E 为总光能。将 \(d\alpha \approx -(l_R/l_L) d\theta\) 带入下式

\[\begin{aligned} \eta_{\mathrm{ge}}&=\frac{1}{\pi}[\alpha_0+\int_{\alpha_0}^{\pi}\frac{r_R}{r_L}\frac{l_L}{l_R}d\alpha]\\ &=\frac{1}{\pi}[\alpha_0+\frac{r_R}{r_L}\theta_0] \end{aligned} \]

由此转换为 \(\alpha_{0}\) 和 \(\theta_{0}\) 代求

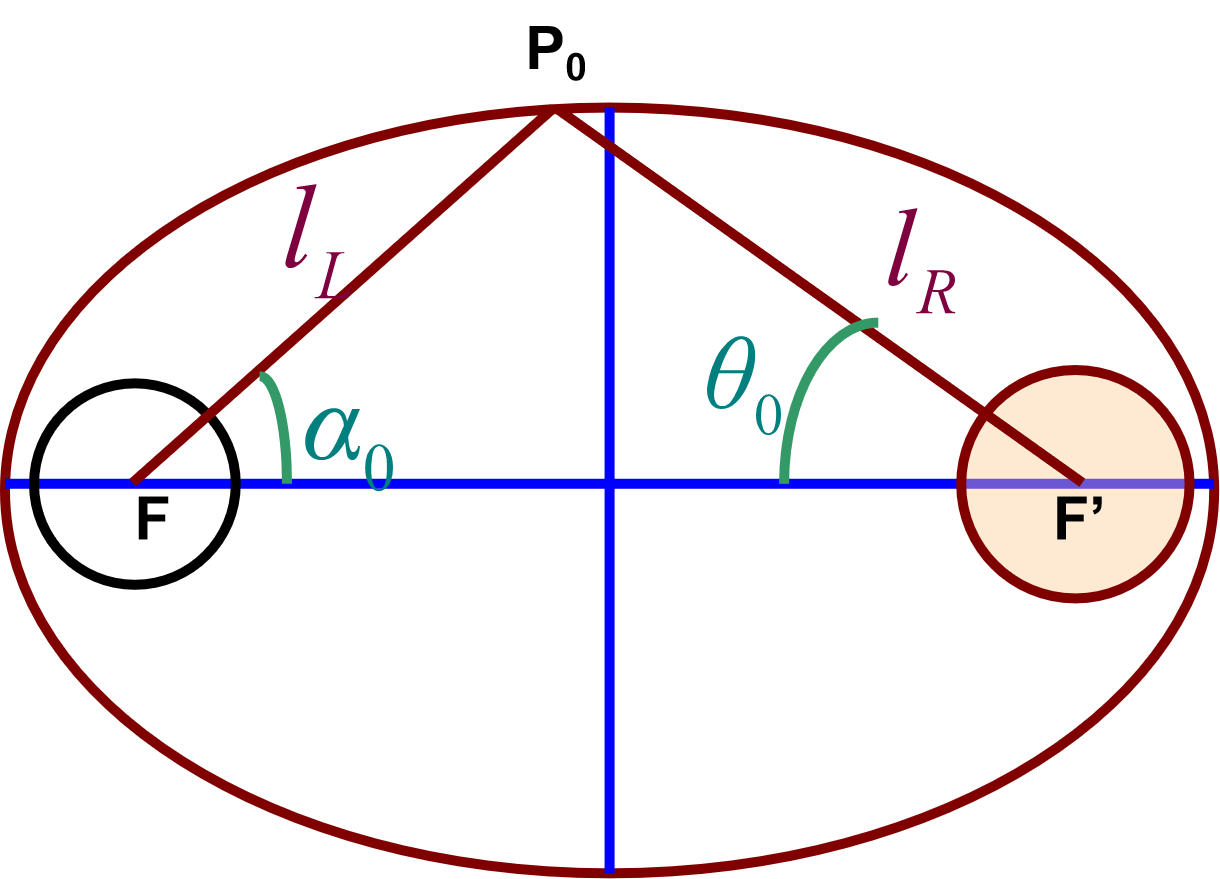
\(P_0\) 点的确定

\(P_0\) 可以根据下列公式进行确定

\[\begin{cases} l_L+l_R = 2a\\ \frac{r_R}{r_L}=\frac{l_R}{l_L}\\ \cos \alpha _0 =\frac{l_{L}^{2}+4c^2-l_{R}^{2}}{4l_Lc}\\ e =\frac{c}{a}\\ \end{cases}\,\,\Longrightarrow \,\, \left\{ \begin{aligned} \cos \alpha _0&=\frac{1}{e}[1-\frac{1-e^2}{2}(1+\frac{r_R}{r_L})]\\ &\sin \theta _0 =(\frac{r_L}{r_R})\sin \alpha _0\\ \end{aligned} \right. \]

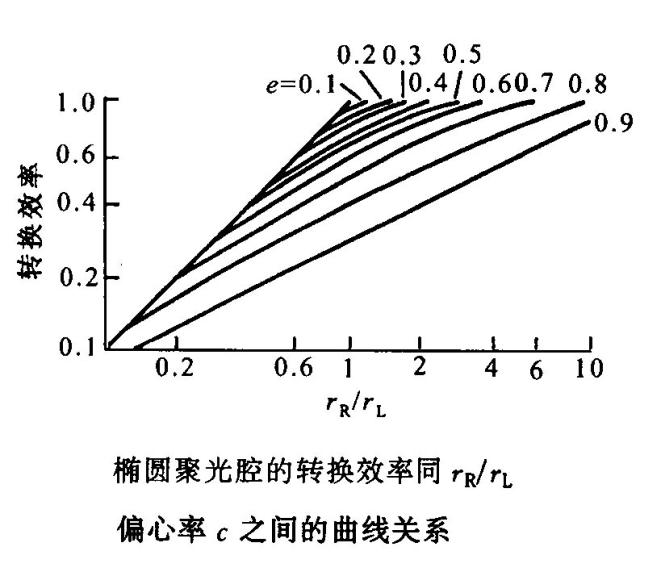
得到椭圆聚光腔的转换效率同 \(\frac{r_R}{r_L}\)和偏心率c的关系

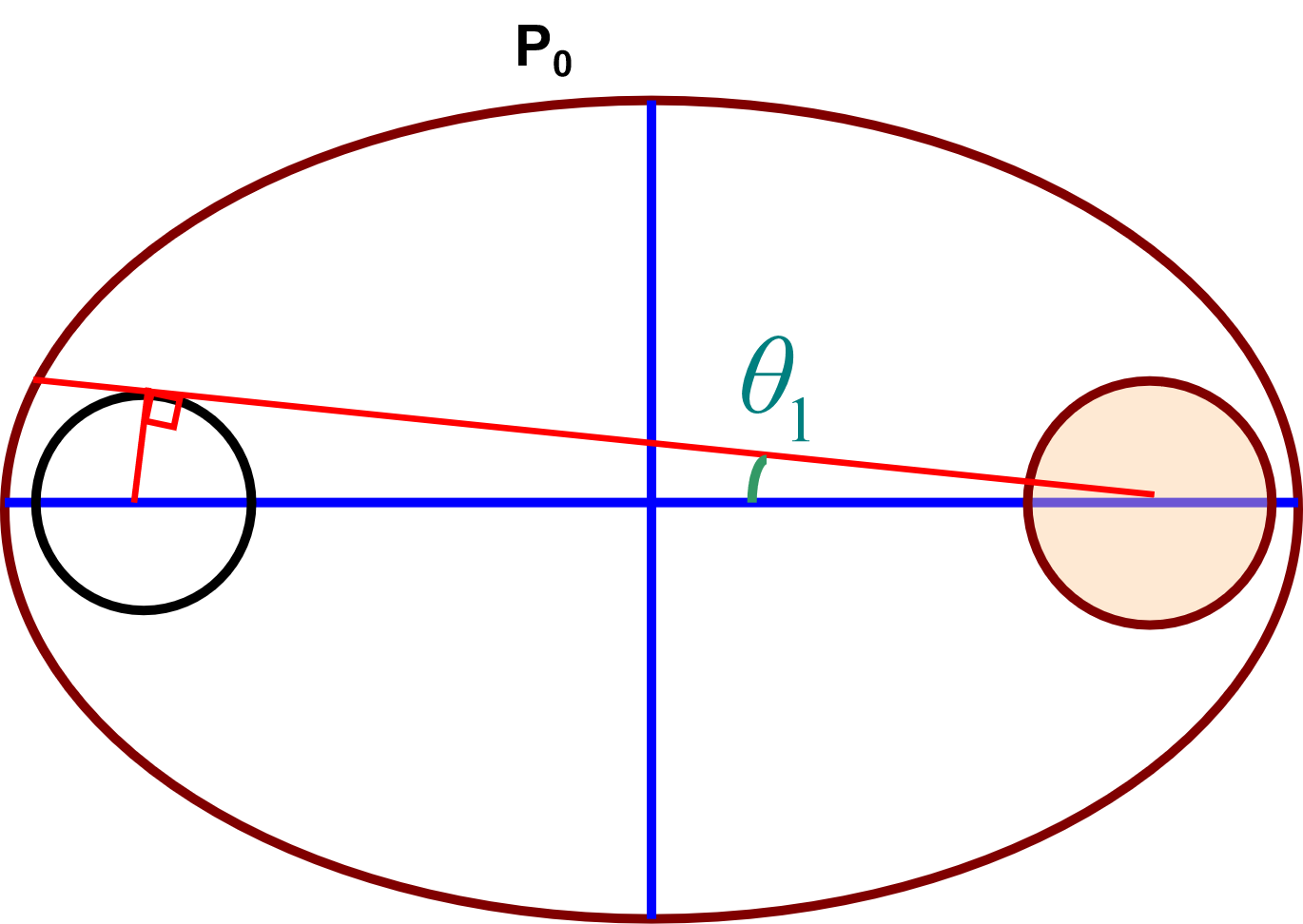
灯的遮挡

\[\begin{equation} \eta_{ge}^{\prime}=\frac{1}{\pi} [\alpha_0+\frac{r_R}{r_L}(\theta_0-\theta_1)] \end{equation} \]

式中，\(\sin\theta_1=\frac{r_L}{2ea}\)

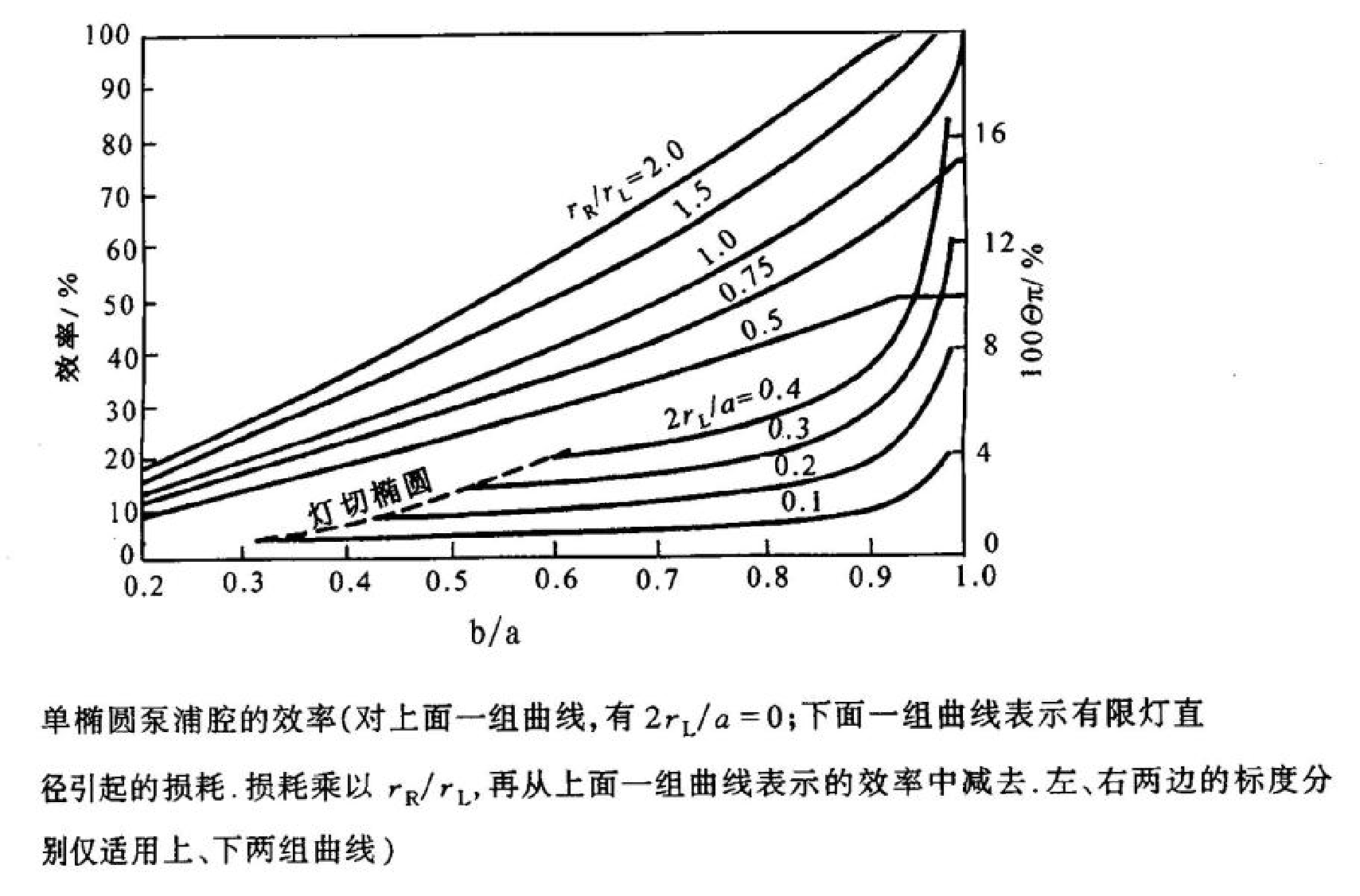
习题

单椭圆柱腔，

a = 32 mm, c = 14 mm
​ \(r_R\) = 5 mm, \(r_L\) = 4 mm
求：\(\eta^{\prime}_{ge}\)

解：

\[\cos \alpha _0 =\frac{1}{e}[1-\frac{1-e^2}{2}(1+\frac{r_R}{r_L})] \\ \sin \theta _0 =(\frac{r_L}{r_R})\sin \alpha _0 \\ \sin \theta _1 =\frac{r_L}{2ae} \\ \eta _{ge}^{\prime}=\frac{1}{\pi}[\alpha _0+\frac{r_R}{r_L}(\theta _0-\theta _1)] \]

漫反射腔的效率

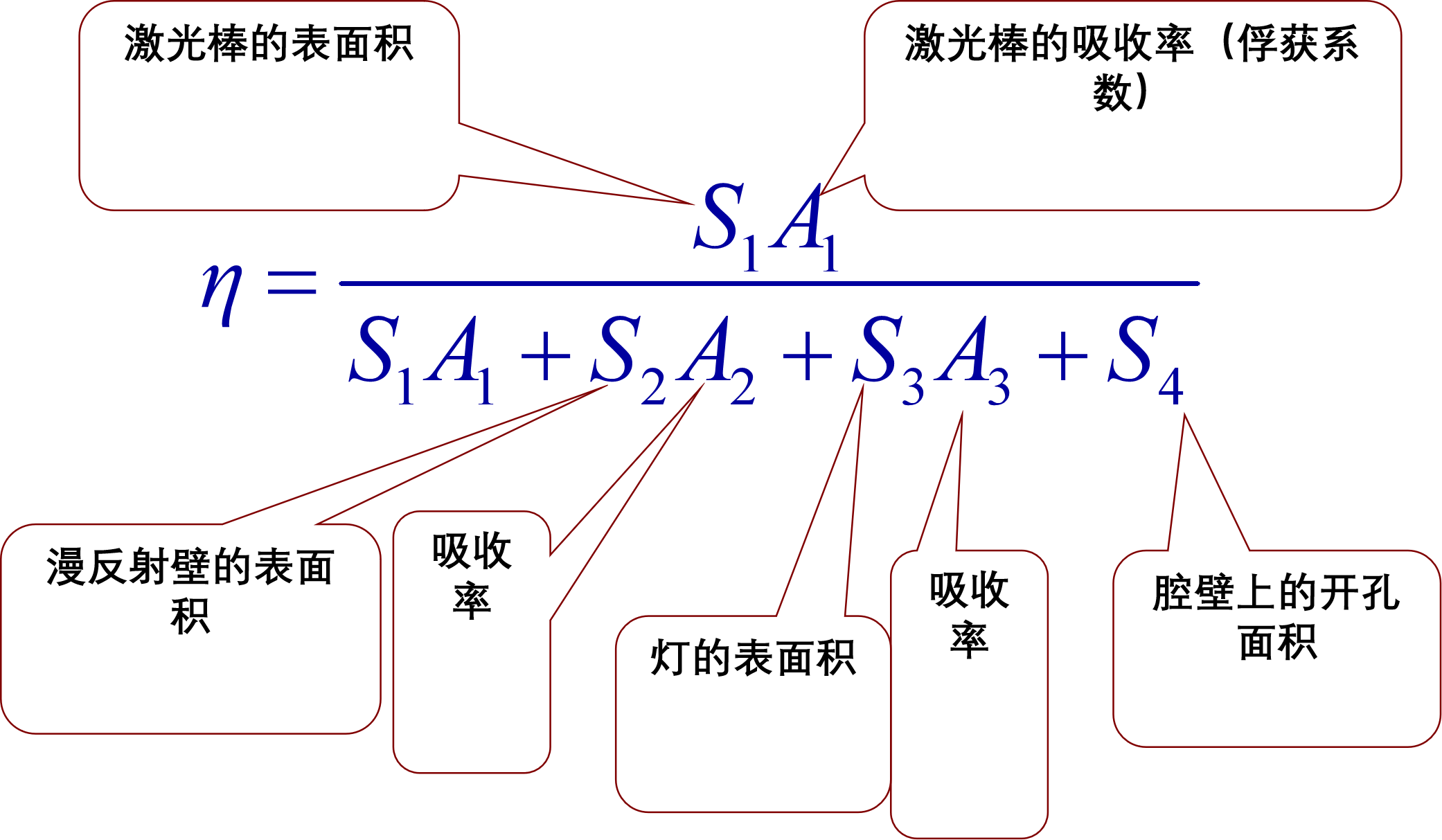
漫反射腔的效率与棒的折射率、半径和吸收系数的关系

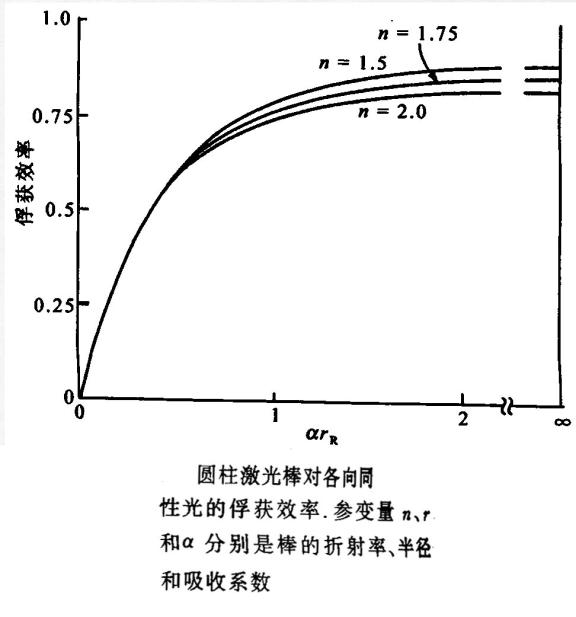
泵浦光在激光棒内分布

增益和温度分布不均的表现

• 起振不均
• 光斑强度不均
• 光学畸变
• 激光效率和发散角变坏
  影响泵浦光分布的因素
• 聚光器的聚光特性
  • 聚焦或漫反射
• 激光棒表面情况
  • 抛光或磨毛
• 激光棒吸收系数与棒半径之积
• 直照情况

均匀光场中棒内光能的分布

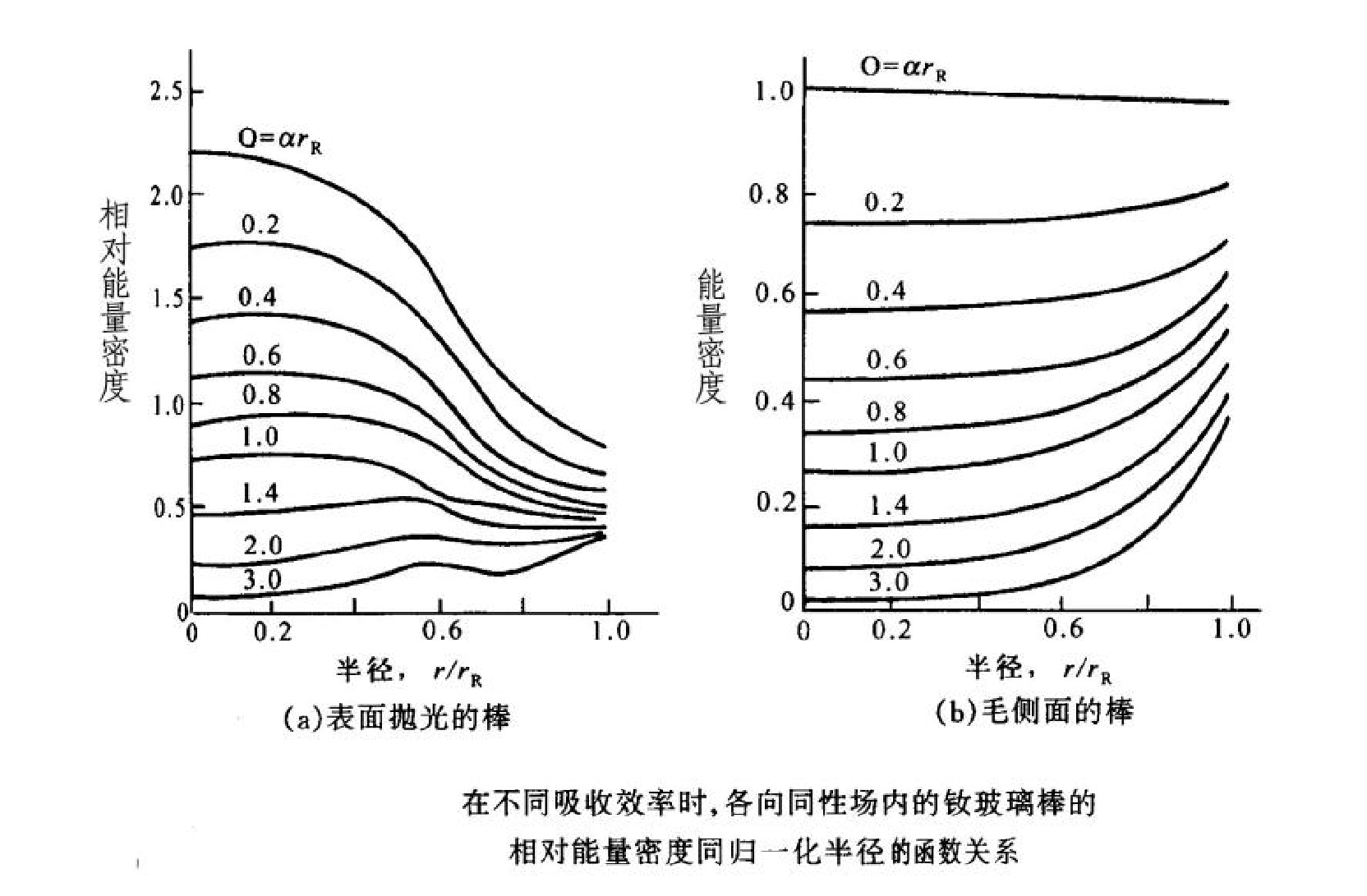
椭圆柱聚光腔的泵浦光分布

\[\begin{gathered} L_{ab}= 2r_L(1+e)/(1-e)\\ L_{cd}= 2r_L(1-e^2)/(1+e^2)\\ L_{ef}= 2r_L(1-e)/(1+e) \end{gathered} \]

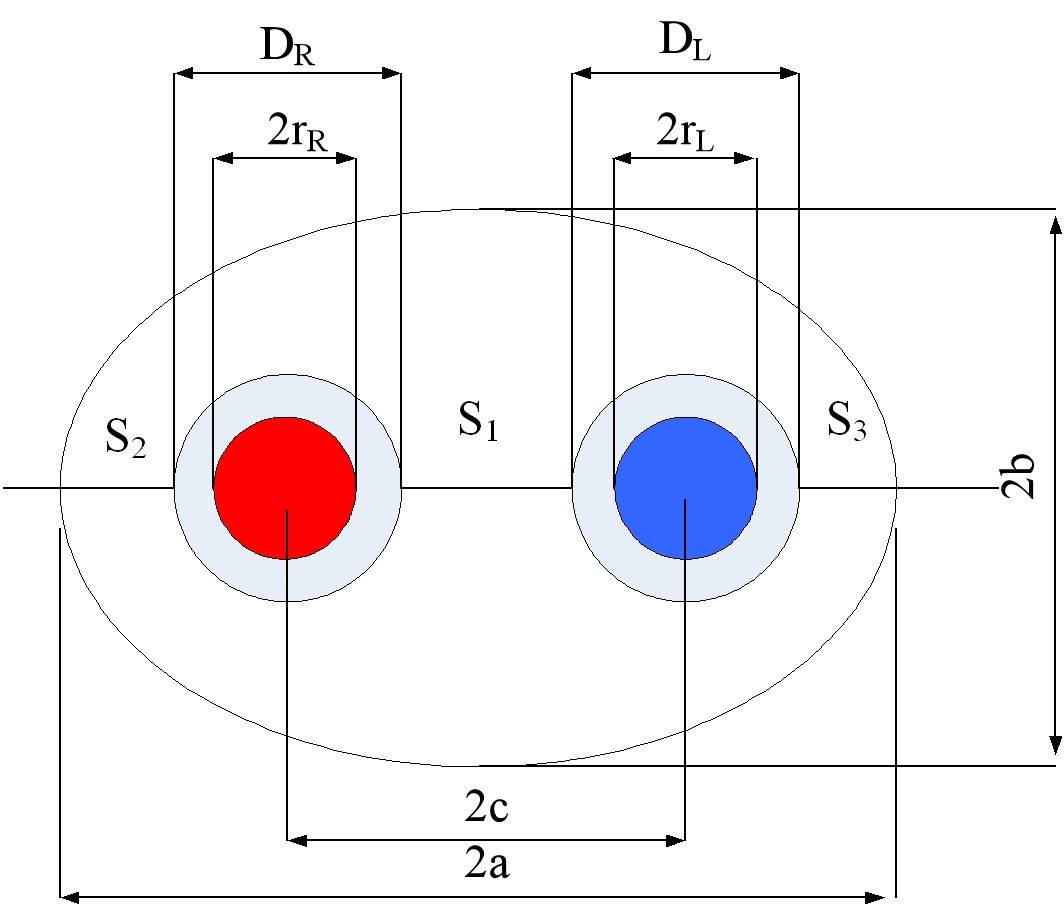
聚光腔的设计

步骤

1. 确定灯棒尺寸 \(r_R\) 、 \(r_L\)

2. 确定 \(D_R\) 、 \(D_L\)

   \(D_R=2r_R+4\sim6mm\)
   ​ \(D_L=2r_L+4\sim6mm\)

3. 确定椭圆腔焦点距离

   \(2C=S_1+\frac{D_R+D_L}{2}\)

4. 确定椭圆腔长轴

   \(2a=S_1+2S_2+D_R+D_L\)

5. 确定椭圆腔短轴

   \(b=\sqrt{a^2-C^2}\)

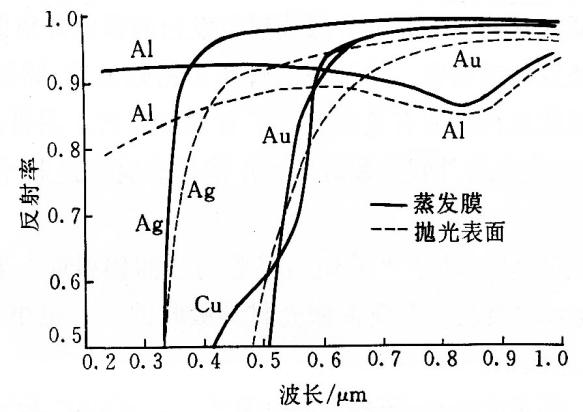
聚光腔常用材料的反射率