Longest common subsequence（LCS）

问题

说明该问题在生物学中的实际意义

Biological applications often need to compare the DNA of two (or more) different organisms. A strand of DNA consists of a string of molecules called bases, where the possible bases are adenine, guanine, cytosine, and thymine（腺嘌呤，鸟嘌呤，胞嘧啶和胸腺嘧啶）. Representing each of these bases by its initial letter, we can express a strand of DNA as a string over the finite set {A, C, G, T}. For example, the DNA of one organism may be S₁ = ACCGGTCGAGTGCGCGGAAGCCGGCCGAA, and the DNA of another organism may be S₂ = GTCGTTCGGAATGCCGTTGCTCTGTAAA. One reason to compare two strands of DNA is to determine how “similar” the two strands are, as some measure of how closely related the two organisms are. We can, and do, define similarity in many different ways. For example, we can say that two DNA strands are similar if one is a substring of the other. In our example, neither S1 nor S2 is a substring of the other. Alternatively, we could say that two strands are similar if the number of changes needed to turn one into the other is small. Yet another way to measure the similarity of strands S1 and S2 is by finding a third strand S3 in which the bases in S3 appear in each of S1 and S2; these bases must appear in the same order, but not necessarily consecutively. The longer the strand S3 we can find, the more similar S1 and S2 are. In our example, the longest strand S3 is GTCGTCGGAAGCCGGCCGAA.

该问题涉及的概念

子序列

given a sequence X = {x₁, x₂, .... , x_m}, another sequence Z = {z₁, z₂, ... ,z_k} is a subsequence of X if there exists a strictly increasing sequence {i₁, i₁, ... , i_k} of indices of X such that for all j = 1, 2, ... , k, we have x_{i_j} = z_j.

子序列要求元素的顺序一致，但是不要求连续。

公共子序列

a sequence Z is a common subsequence of X and Y if Z is a subsequence of both X and Y.

问题形式化定义

Input:

X = <x₁, x₂, .... , x_m>
Y = <y₁, y₂, .... , y_n>

Output

a maximum length common subsequence of X and Y

暴力算法分析

In a brute-force approach to solving the LCS problem, we would enumerate all subsequences of X and check each subsequence to see whether it is also a subsequence of Y, keeping track of the longest subsequence we find. Each subsequence of X corresponds to a subset of the indices {1, 2, ... , m} of X. Because X has 2^m subsequences, this approach requires exponential time, making it impractical for long sequences.

动态规划解法

符号定义

To be precise, given a sequence X = <x₁, x₂, .... , x_m>,we define the ith prefix of X, for i = {0, 1,..., m} as X_i = <x₁, x₂, .... , x_i> . For example, if X = {A, B, C, B, D, A, B},then X₄ = {A, B, C, B} and X₀ is the empty sequence.

优化子结构

Theorem (Optimal substructure of an LCS)

Let X = <x₁, x₂, .... , x_m> and Y = <y₁, y₂, .... , y_n> be sequences, and let Z = {z₁, z₂, ... ,z_k} be any LCS of X and Y.

If x_m = y_n, then z_k = x_m = y_n and Z_k-1 is an LCS of X_{m- 1} and Y_n-1.
If x_m != y_n, then z_k != x_m implies that Z is an LCS of X_m-1 and Y.
If x_m != y_n, then z_k != y_n implies that Z is an LCS of X and Y_n-1.

Proof

(1)

If z_k != x_m , then we could append x_m = y_n to Z to obtain a common subsequence of X and Y of length k + 1, contradicting the supposition that Z is a longest common subsequence of X and Y. Thus, we must have z_k = x_m = y_n .

Now, the prefix Z_k-1 is a length-(k-1) common subsequence of X_m-1 and Y_n-1. We wish to show that it is an LCS. Suppose for the purpose of contradiction that there exists a common subsequence W of X_m-1 and Y_n-1 with length greater than k - 1. Then, appending x_m = y_n to W produces a common subsequence of X and Y whose length is greater than k, which is a contradiction.

(2)

If z_k != x_m, then Z is a common subsequence ofX_m-1 and Y. If there were a common subsequence W ofX_m-1 and Y with length greater than k ,then W would also be a common subsequence of X_m and Y, contradicting the assumption that Z is an LCS of X and Y.

(3)

The proof is symmetric to (2).

子问题重叠性

To find an LCS of X and Y, we may need to find the LCSs of X and Y_n-1 and of X_m-1 and Y. But each of these subproblems has the subsubproblem of finding an LCS of X_m-1 and Y_n-1. Many other subproblems share subsubproblems.

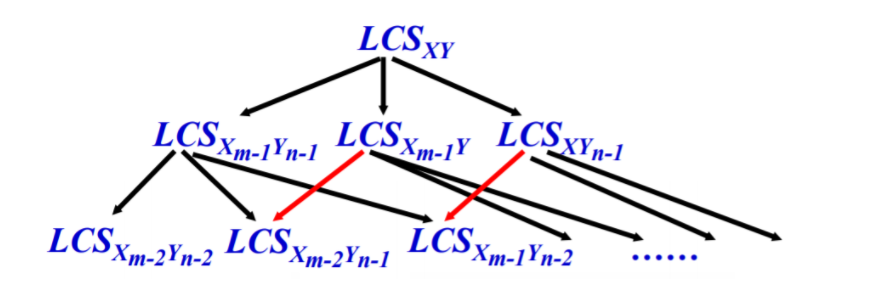
递归的定义优化解的代价

Let us define c[i, j] to be the length of an LCS of the sequences X_i and Y_j.

If either i = 0 or j = 0, one of the sequences has length 0, and so the LCS has length 0. The optimal substructure of the LCS problem gives the recursive formula

c[ i,j ] = 0, if i = 0 或 j = 0
c[ i,j ] = c[ i-1,j-1] + 1, if i,j >0 且 X_i = Y_j
c[ i,j ] = max{ c[i, j-1], c[i-1, j]}, if i,j >0 且 X_i != Y_j

计算优化解的代价算法

bottom-up method

LCS-length_bottomup(X, Y)
m = length(X)；
n = length(Y)；
For i = 1 To m Do
      C[i,0] = 0;
For j = 1 To n Do
      C[0,j] = 0;
For i = 1 To m Do
     For j = 1 To n Do
          If Xi == Yj
             Then C[i,j] = C[i-1,j-1]+1；B[i,j] = “↖”;
          Else If C[i-1,j]  <  C[i,j-1]
             Then C[i,j] = C[i-1,j];
                     B[i,j] = “↑”;
          Else     
                      C[i,j] = C[i,j-1];
                      B[i,j] = “←”;
Return C and B

top-down with memoization

LCS-LENGTH-topdown( X, Y, m ,n )
Let b[0..m][0..n] be an new array
for i = 1 to m
    for j = 1 to n
        b[i][j] = -1
return LCS-LENGTH-AUX(X, Y, m ,n ,b ,s)

       
LCS-LENGTH-AUX(X, Y, i ,j ,b ,s)
if b[i][j] != -1
    return b[i][j] && s
if i = 0 || j = 0
    b[i][j] = 0
else if X[i] == X[j]
    b[i][j] = LCS-LENGTH-AUX(X, Y, i-1 ,j-1 ,b ,s) + 1
else 
    b[i][j] = LCS-LENGTH-AUX(X, Y, i-1 ,j ,b ,s) > LCS-LENGTH-AUX(X, Y, i ,j-1 ,b ,s) ? LCS-LENGTH-AUX(X, Y, i ,j-1 ,b ,s):LCS-LENGTH-AUX(X, Y, i-1 ,j ,b ,s)
return b[i][j]

实际代码

#include<stdio.h>
#include<string.h>

#define M 7
#define N 6

void LCS_length_bottomup(char* x, char* y);
void LCS_length_updown(char* x, char* y);
int LCS_length_AUX(char* x, char* y, int i, int j, int b[M + 1][N + 1], char s[M + 1][N + 1]);

void main() {
	char x[M + 1] = { ' ', 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
	char y[N + 1] = { ' ','B','D','C','A','B','A' };
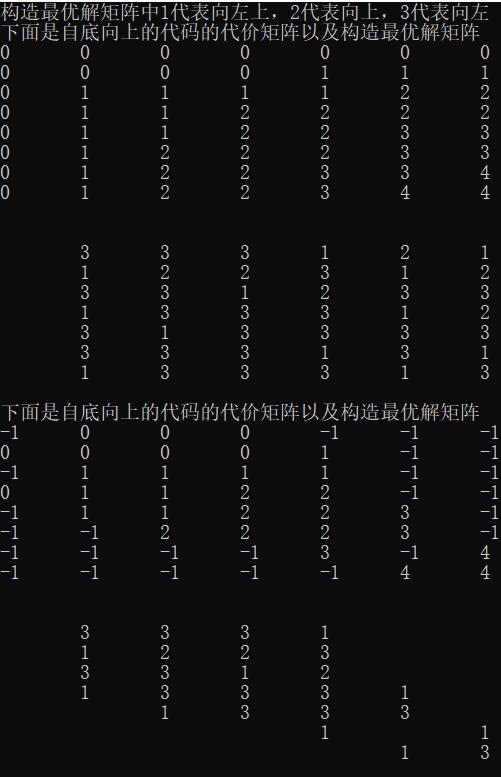
	printf("构造最优解矩阵中1代表向左上，2代表向上，3代表向左\n");
	printf("下面是自底向上的代码的代价矩阵以及构造最优解矩阵\n");
	LCS_length_bottomup(x, y);
	printf("下面是自底向上的代码的代价矩阵以及构造最优解矩阵\n");
	LCS_length_updown(x, y);
}

void LCS_length_updown(char* x, char* y) {
	int b[M + 1][N + 1];
	char s[M + 1][N + 1];
	memset(b, -1, (M + 1) * (N + 1) * sizeof(int));
	memset(s, ' ', (M + 1) * (N + 1) * sizeof(char));
	LCS_length_AUX(x, y, M, N, b, s);
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%d	", b[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%c	", s[i][j]);
		}
		printf("\n");
	}
	printf("\n");
}

int LCS_length_AUX(char* x, char* y,int i, int j, int b[M + 1][N + 1], char s[M + 1][N + 1]){
	if (b[i][j] != -1) return b[i][j];
	if (i == 0 || j == 0) {
		b[i][j] = 0;
	}
	else if (x[i] == y[j]) {
		b[i][j] = LCS_length_AUX(x, y, i-1, j-1, b, s) + 1;
		s[i][j] = '1';//左上
	}
	else {
		int p = LCS_length_AUX(x, y, i , j - 1, b, s);
		int q = LCS_length_AUX(x, y, i - 1, j , b, s);
		if (p > q) {
			b[i][j] = p;
			s[i][j] = '2';//上
		}
		else {
			b[i][j] = q;
			s[i][j] = '3';//左
		}
	}
	return b[i][j];
}

void LCS_length_bottomup(char *x, char *y) {
	int b[M + 1][N + 1];
	char s[M + 1][N + 1];
	memset(b, -1, (M + 1) * (N + 1) * sizeof(int));
	memset(s, ' ', (M + 1) * (N + 1) * sizeof(char));
	for (int i = 0; i <= M; i++) 
		b[i][0] = 0;
	for (int i = 0; i <= N; i++)
		b[0][i] = 0;
	for (int i = 1; i <= M; i++) {
		for (int j = 1; j <= N; j++) {
			if (x[i] == y[j]) {
				b[i][j] = b[i - 1][j - 1] + 1;
				s[i][j] = '1';//左上
			}
			else if (b[i - 1][j] < b[i][j - 1]) {
				b[i][j] = b[i][j - 1];
				s[i][j] = '2';//上
			}
			else {
				b[i][j] = b[i - 1][j];
				s[i][j] = '3';//左
			}
		}
	}
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%d	", b[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	for (int i = 0; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			printf("%c	", s[i][j]);
		}
		printf("\n");
	}
	printf("\n");
}

下面是输出结果，极为有趣的是，从这里可以看出这两种构造方法的区别，一种完全遍历，一种只会遍历其需要的单位。

构造优化解算法

Print-LCS(B, X, i, j)
IF i=0 or j=0 THEN Return;
IF B[i, j]=“↖” 
     Print-LCS(B, X, i-1, j-1);
     Print Xi;
ELSE If B[i, j]=“↑”
     THEN Print-LCS(B, X, i-1, j);
ELSE
     Print-LCS(B, X, i, j-1)

实际代码：

void Print_LCS(char s[M + 1][N + 1], char* x, int i, int j) {
	if (i == 0 || j == 0)
		return;
	if (s[i][j] == '1') {
		Print_LCS(s, x, i - 1, j - 1);
		printf("%c	", x[i]);
	}
	else if (s[i][j] == '2') {
		Print_LCS(s, x, i , j - 1);
	}
	else {
		Print_LCS(s, x, i - 1, j);
	}	
}

这里给出一个例子：

X = <A, B, C, B, D, A, B>

Y = <B, D, C, A, B, A>

算法复杂度说明

时间复杂度：

计算代价的时间：O(mn)，每一个单元的填充需要Θ(1)。
构造最有解的时间：O(m+n)。

The procedure takes time O(m + n), since it decrements at least one of i and j in each recursive call.

对于代码的改善

Once you have developed an algorithm, you will often find that you can improve on the time or space it uses. Some changes can simplify the code and improve constant factors but otherwise yield no asymptotic improvement in performance. Others can yield substantial asymptotic savings in time and space.

In the LCS algorithm, for example, we can eliminate the b table altogether. Each c[i, j] entry depends on only three other c table entries: c[i-1, j] && c[i, j-1] && c[i-1, j-1]. we can determine in O(1) time which of these three values was used to compute c[i, j] without inspecting table b. Thus, we can reconstruct an LCS in O(m + n) time using a procedure similar to PRINT-LCS. Although we save Θ(mn) space by this method, the auxiliary space requirement for computing an LCS does not asymptotically decrease, since we need Θ(mn) space for the c table anyway. We can, however, reduce the asymptotic space requirements for LCS-LENGTH,

since it needs only two rows of table c at a time: the row being computed and the previous row. This improvement works if we need only the length of an LCS; if we need to reconstruct the elements of an LCS, the smaller table does not keep enough information to retrace our steps in O(m + n) time.

伪代码：2 min(m, n) entries in the c table plus O(1) additional space*

LCS-length_bottomup(X, Y)
m = length(X);
n = length(Y);
let p[0..1][1...min(m,n)]  be a new array
for i = 1 to min(m,n) do
    p[0,i] = 0
for i = 1 To max(m,n) Do
     For j = 1 To min(m,n) Do
          If Xi == Yj
             Then p[i%2,j] = p[(i-1)%2,j-1]+1;
          Else If p[(i-1)%2,j]  <  C[i%2,j-1]
             Then p[i%2,j] = p[(i-1)%2,j];
          Else     
                  p[i%2,j] = p[i%2,j-1];
Return p[max(m,n),min(m,n)]

下面是实际代码

#include<stdio.h>
#include<string.h>

#define M 7
#define N 6

void LCS_length_2min(char* x, char* y);

void main() {
	char x[M + 1] = { ' ', 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
	char y[N + 1] = { ' ','B','D','C','A','B','A' };
	LCS_length_2min(x, y);
}

void LCS_length_2min(char* x, char* y) {
	// M >= N
	int P[2][N + 1];
	for (int i = 0; i <= N; i++) {
		P[0][i] = 0;
	}
	P[1][0] = 0;
	for (int i = 1; i <= M; i++) {
		for (int j = 1; j <= N; j++) {
			if (x[i] == y[j]) {
				P[i % 2][j] = P[(i - 1) % 2][j - 1] + 1;
			}
			else if (P[(i - 1) % 2][j] > P[(i) % 2][j - 1]) {
				P[i % 2][j] = P[(i - 1) % 2][j];
			}
			else {
				P[i % 2][j] = P[(i) % 2][j - 1];
			}
		}
	}
	printf("%d\n", P[M % 2][N]);
}

伪代码： min(m, n) entries in the c table plus O(1) additional space

LCS-length_bottomup(X, Y)
m = length(X);
n = length(Y);
Leftentry = 0;//保存当前计算代价的左上代价
LeftUpentry = 0;//保存当前代价的左代价，其实可以不使用，直接比较p[j-1]和p[j]，但是为了保证代码的统一性，即0的情况，故采用一个单独变量
let P[1...min(m,n)]  be a new array;
for i = 1 to min(m,n) do
    P[i] = 0;
for i = 1 To max(m,n) Do
     For j = 1 To min(m,n) Do
          If Xi == Yj
             Then transition = P[j];
                  //由于下一次循环需要使用被覆盖的P[j],但又不可以直接赋值到LeftUpentry中，设置过渡变量
                  P[j] = LeftUpentry + 1;
                  LeftUpentry = transition;
                  Leftentry = P[j];
          Else If Leftentry  <  P[j]
             Then LeftUpentry = P[j];
                  Leftentry = P[j];
          Else     
                  LeftUpentry = P[j];
                  P[j] = Leftentry;
                  Leftentry = P[j];
     Leftentry = 0;
     LeftUpentry = 0;
Return p[min(m,n)]