图神经网络

图与节点的基本

图直径：

图中所有的两两节点他们的最短路径的最大值。·

节点的度中心性：

公式Ndegree/(n-1)   也就是该节点的度/(全部的节点-1)

节点的特征向量中心性Eigenvector Centrality：

如果一个节点连接的度越多，其特征向量中心性越大。

中介中心性Betweenness Centrality :

经过该节点的最短路径/其余两两节点的最短路径。

 

先来看曹操的betweenness的计算，分子的第一项：蔡文姬出发到甄姬的最短路径没有经过曹操，所以为0，假设蔡文姬出发去周瑜的最短路径经过曹操所以为1，从蔡文姬出发去夏侯惇的最短路径经过曹操所以为1，从蔡文姬出发前往典韦的最短路径有两条(都是要经过一个人才到)里面有一条是经过曹操的所以其为0.5,所以分子的第一项为(0+1+1+0.5)。分子的第二项：从甄姬出发到蔡文姬的最短路径不经过曹操所以为0，从甄姬出发到典韦的最短路径不经过曹操所以为0，从甄姬出发到周瑜的最短路径经过曹操所以其为1，从甄姬出发到夏侯惇的最短路径经过曹操，所以其为1，所以分子的第二项为(0+0+1+1)。后面的也是同样来类推。来看分母，先是蔡文姬去除了曹操以外的所有人总共有4条最短路径，除了曹操之外总共有5个人，所以分母为5*4

 连接中心性closeness

 

 

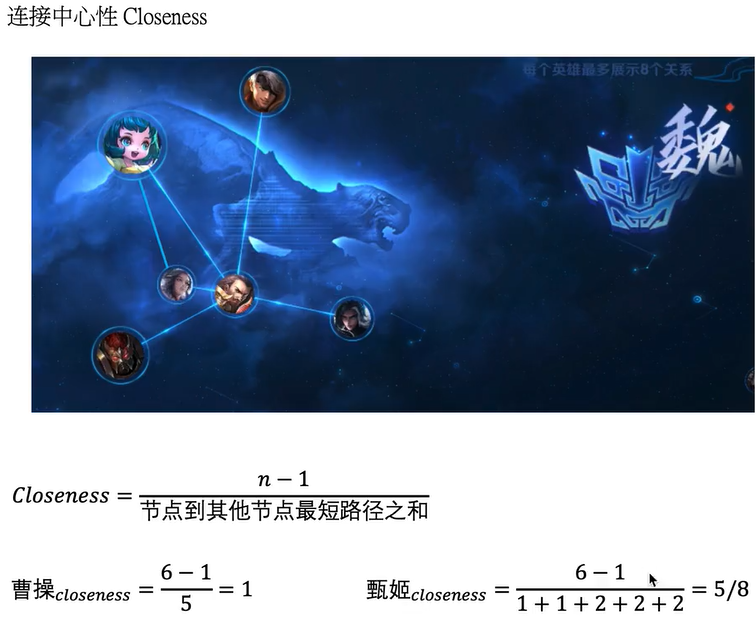
计算曹操的closeness:分子是全部节点的个数-1，任意两个节点之间的距离为1，曹操到任意的其他5个人的距离均是为1，所以分母为5。

再计算甄姬的closeness:分子是全部节点的个数-1，甄姬到曹操和蔡文姬的最短路径是1，而到典韦，夏侯惇，周瑜都需要经过曹操，所以最短距离是2。

网页排序算法pageRank

如果一个网页被很多其他网页所链接，那么说明他受到普遍的承认和信赖，那么他的排名就高。PR值越高说明该网页越受欢迎（越重要

假设一个由只有4个页面组成的集合：A，B，C和D。如果所有页面都只链向A，那么A的PR（PageRank）值将是B，C及D的和。

换句话说，根据链出总数平分一个页面的PR值。

 

 

 

 

 

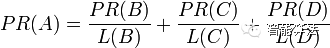
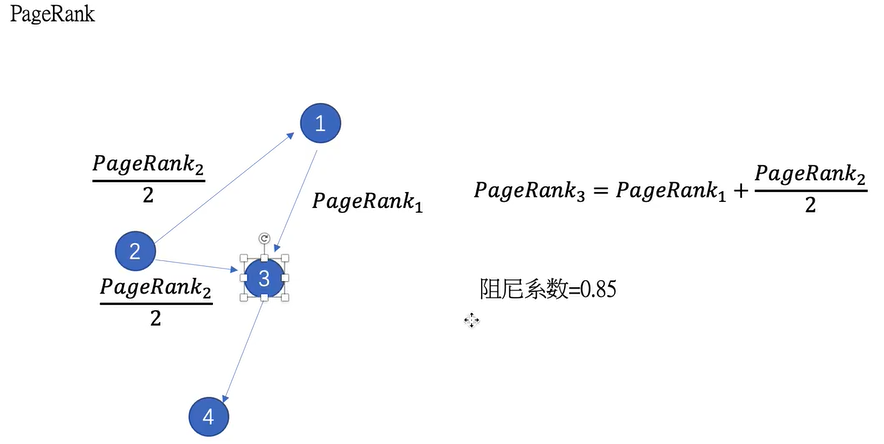
使用networkx进行计算

import numpy as np
import pandas as pd
import networkx as nx

edges = pd.DataFrame()  #使用pd构造dataframe
edges["sources"] = [1,1,2,2,3,3,4,4,5,5]  #构造源节点列表
edges["targets"] = [2,4,5,3,1,2,5,1,3,4]  #构造目标节点列
edges["weights"] = [1,1,1,1,1,1,1,1,1,1]  #构造边的权重列
#使用pandas来生成图，比如从1出发到2，权重是1，从1出发到4权重也是1
Graph = nx.from_pandas_edgelist(edges,source="sources",target="targets",edge_attr="weights")
print(nx.degree(Graph)) #打印每一个节点的度
print(list(nx.connected_components(Graph))) #打印连通的成分
print(nx.diameter(Graph)) #打印图直径，图上的任意两个相邻的点之间的路径的最大值为图直径
print(nx.degree_centrality(Graph)) #打印度中心性
print(nx.eigenvector_centrality(Graph)) #打印特征向量中心性
print(nx.betweenness_centrality(Graph)) #betweenness_centrality
print(nx.closeness_centrality(Graph)) #closeness_centrality
print(nx.pagerank(Graph)) #pagerank
print(nx.hits(Graph)) #hits

网络表示学习（Graph Embedding）

网络表示学习又称图嵌入（Graph Embedding），主要目的是将一个网络中的节点基于网络的特点映射成一个低维度向量，这样可以定量的衡量节点之间的相似度，更加方便的应用。

Graph Embedding的常用算法deepwalk,line,sdne,node2vec,struc2vec。

过去用来表示每个节点可以使用onehont编码，10个节点就需要10维向量，因此缺点主要有两个，当节点多的时候，会使得表示的维度非常的大，第二个缺点是使用onehot编码会丢失掉网络的空间连接信息。

Deepwalk(深度游走)

Deepwalk是一种图结构数据挖掘算法，该算法能够学习网络的隐藏信息，能够将图中的节点表示为一个包含潜在信息的向量。

deepwalk用于将graph向量化 以便后续的深度学习

主要参考文章https://zhuanlan.zhihu.com/p/58105731

 

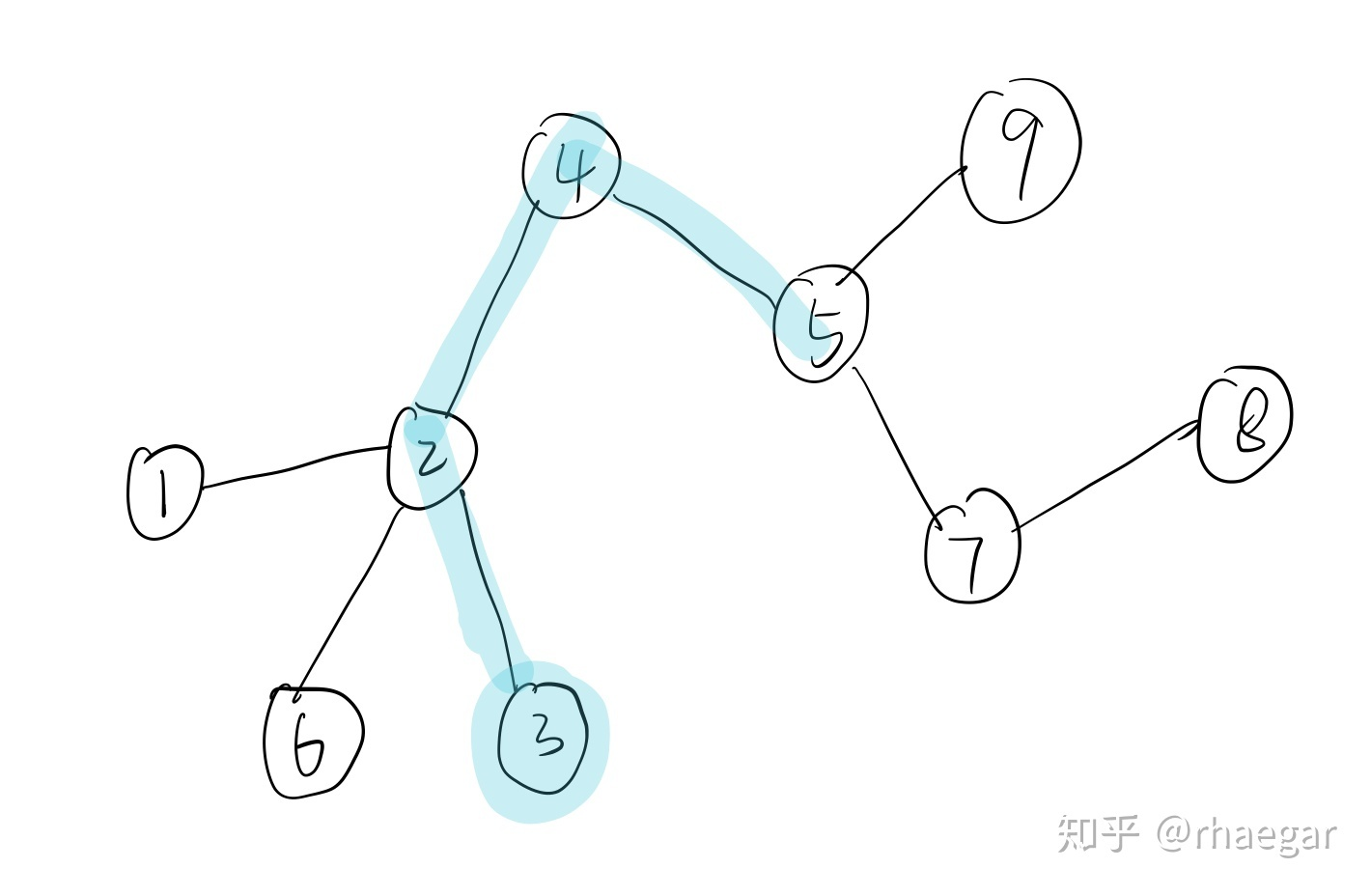
给定一个图，现在首先随机初始点，然后让其自己在此图上走，走出一条路线。经过多次此过程便会得到许多条路线。

这条路径上临近点与点之间必然联系密切有共同特征。现在假设将路线3-2-4-5当作一个句子，各个顶点为句子中单词。

假设这个图上有10000个顶点，就暂时将这10000个顶点的编码方式使用onehot编码。现在要训练出一个用于向量化的神经网络，可以将[1,10000]的定点向量转换成[1,h]的向量。

 

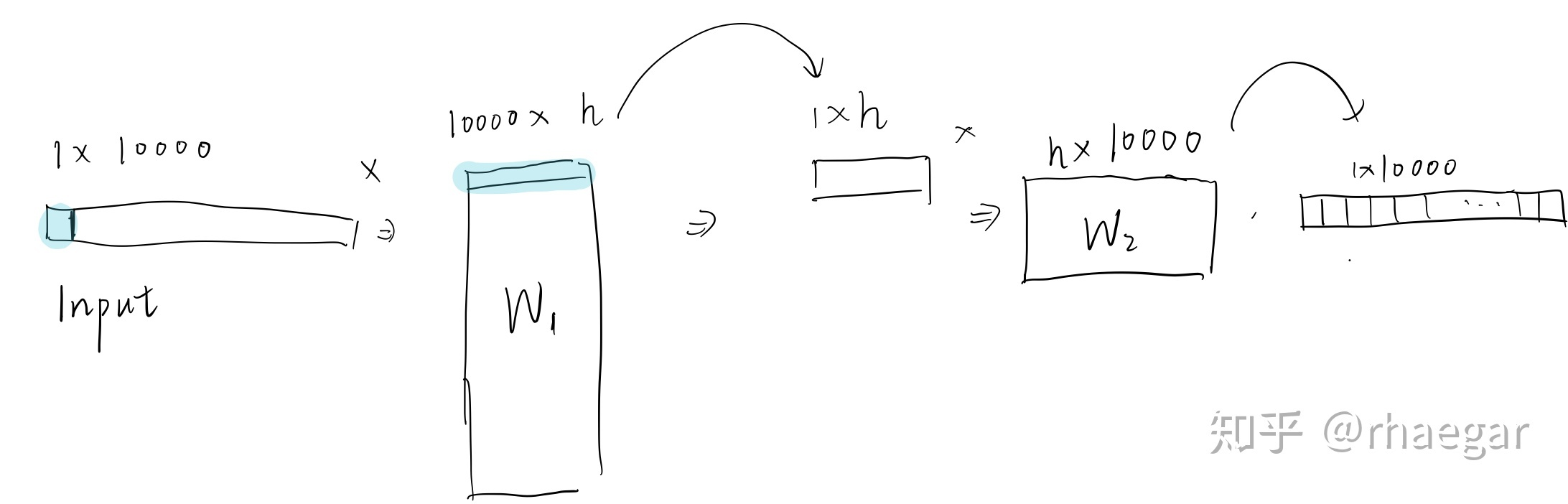
训练网络示意图如上。 

输入为某个顶点，通过10000*h的W矩阵 变成了h长度的向量，再通过h*10000的矩阵变回10000长度的向量。

 

目的是输入一个顶点后 在1*10000的输出结果中 那些与输入点关系密切的位置得分（数值）较高

（回到之前的graph， 比如输入为2的向量， 与2关系密切的点都在之前random walk所制造的“句子”中 即为3 4 5，于是我们训练网络目的是让输出向量第3 4 5维度的得分较大）

通过deepwalk得到了许多的“句子” 即为我们的训练集

当网络训练成熟后，形象理解，我们已经将每个vertex的特征刻画在了neural network里的参数中，于是可以通过截断神经网络到[1,h]的部分来使得输入任意一个[1,10000]的顶点向量

来得到[1,h]的向量。

LINE

deepwalk主要是用在无向图上，LINE可以用在有向图上

LINE考虑了一节相似性和二阶相似性。

 

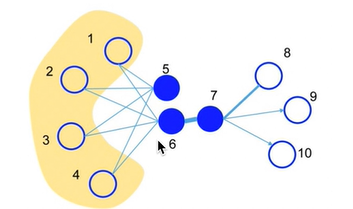
一阶相似性：局部的结构信息。比如6号节点和七号节点，他们是互相相连的而且它们之间的权值很大，所以认为他们是相似的。

二阶相似性：节点的邻居。共享邻居的节点可能是相似的，比如说5号节点和6号节点，他们两个虽然没有直接连接，但是他们同样的连接了1234四个节点，所以我们同样也认为他们是相似的。

 

首先会随机初始化所有节点 的embedding，需要在不断地训练中使用一阶相似性优化这个embedding。

 一阶相似性的计算：

首先需要对任意的两个节点来计算联合概率分布，联合概率分布的计算公式如图所示，就是将两个节点的embedding进行乘积然后计算一下它的sigmoid。

接着是计算任意两个节点之间的经验概率分布，就是将该两个节点间的权重除以所有的权重和

 

 GCN

 

A是邻接矩阵，A~是A矩阵加上单位阵(加上自连接的边)，D~矩阵是将A~矩阵按行进行求和，实际上D~就是A~矩阵的度。D~-1/2是使用D~进行计算出来的

H(l)是当前的节点的表示H(l+1)是节点在下一层的表示，是当前节点的特征，将当前节点的特征乘以当前节点再乘以权重即刻得到GCN中的下一层节点的表示。

 

 先考虑没有D矩阵的情况，只有邻接矩阵的情况

 

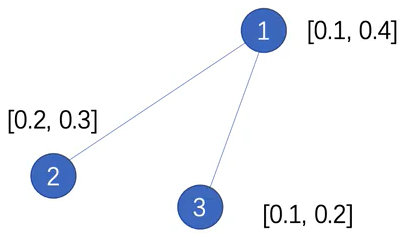
左边的是邻接矩阵，右边的是特征矩阵，可以看见相乘之后对于1节点来说0.2+0.1就是融合了其他两个节点的特征，0.3+0.2也是融合了其他两个连接的节点的特征。

对于2号节点来说，由于只有1号节点与其相连，所以融合的特征只有融合了1号节点的特征。

 

再考虑没有D矩阵的情况，用A~矩阵的情况。在这种情况下，A~实际上是加上了自连接后的邻接矩阵。可以看见其在乘以特征之后，它不仅融合了相邻节点的特征，他还融合了自己的特征

 原式左边和右边乘以D1/2的原因：

 

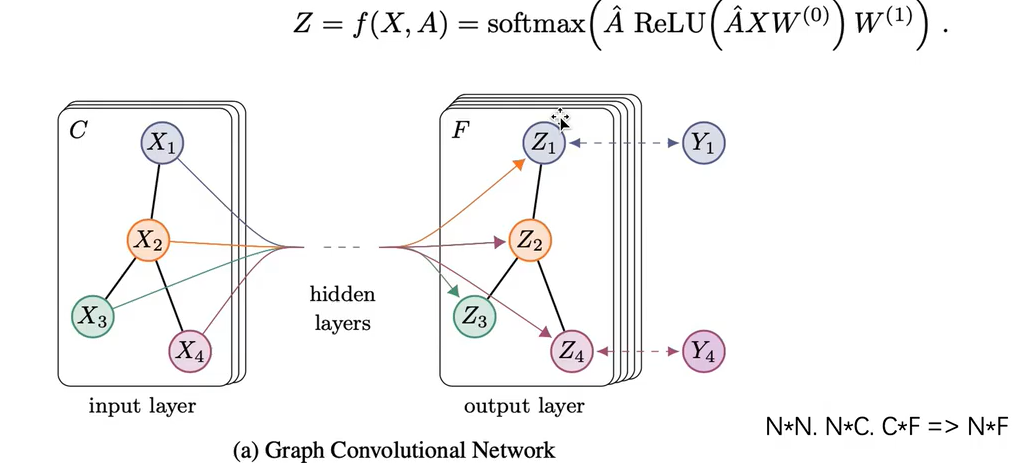
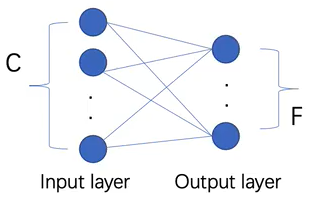
GNN做分类任务：首先输入一个图,然后经过中间的神经网络得到右边的输出层，C是左边原始输入的特征的维度，右边经过神经网络之后变成了F维度的特征输出。然后将输出层进行softmax输出概率，然后接上全连接层训练标签

 

GraphSAGE

 

 GCN和graphsage的相同点，他们都是将节点的邻居的信息进行聚合成下一层 的表示。不同点是GCN是只能在它只能处理所有之前出现在图中的节点，对于没有看过的节点是不能处理的。而GRAPHSAGE不仅仅限于图中的节点，它也可以聚合周围的邻居节点的特征。

 

N(1)代表着是一号节点，代表了1节点在第1层的邻居向量。现在已知的是图还有（也就是1节点在第0层的特征向量）现在要求也就是1节点在第1层的特征向量。

首先是找出1节点的所有的邻居节点，也就是3，4，5，6。将所有的邻居节点通过AGGREGATE聚合函数将他们在第0层的特征向量给聚合起来合成。接着是将和1节点在第0层的特征向量拼接起来并乘以可自主学习的权重矩阵w最终得到。

 

采样：如果每次对这个点的所有邻居都进行聚合的话，在邻居非常多的时候时间复杂度可能会提升很多，因此，规定采样大小(采用固定的抽样大小)。这个时候便会遇到两种情况，当前所有的邻居的数量小于采样长度时，先把所有的邻居不重复的采样过之后再随机采样邻居去填充满采样长度。当当前所有的邻居的数量大于采样长度的时候，从邻居中不重复地抽出采样长度个。

对于聚合函数的要求

 聚合函数应该是对称的，不要求输入是有顺序的(也就是说输入x1,x2,x3得到一个值，输入x2,x3,x1也应该是得到一个相同的值。)

1.均值聚合

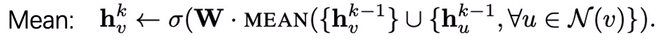
2.LSTM聚合

3.pooling聚合

 Minbatch

由于graphsage和普通的GCN不同，GCN是需要全图的信息的，而Graphsega只需要知道当前要计算的这个节点的邻居节点，使得其在大规模的图上面进行计算变得可行

 

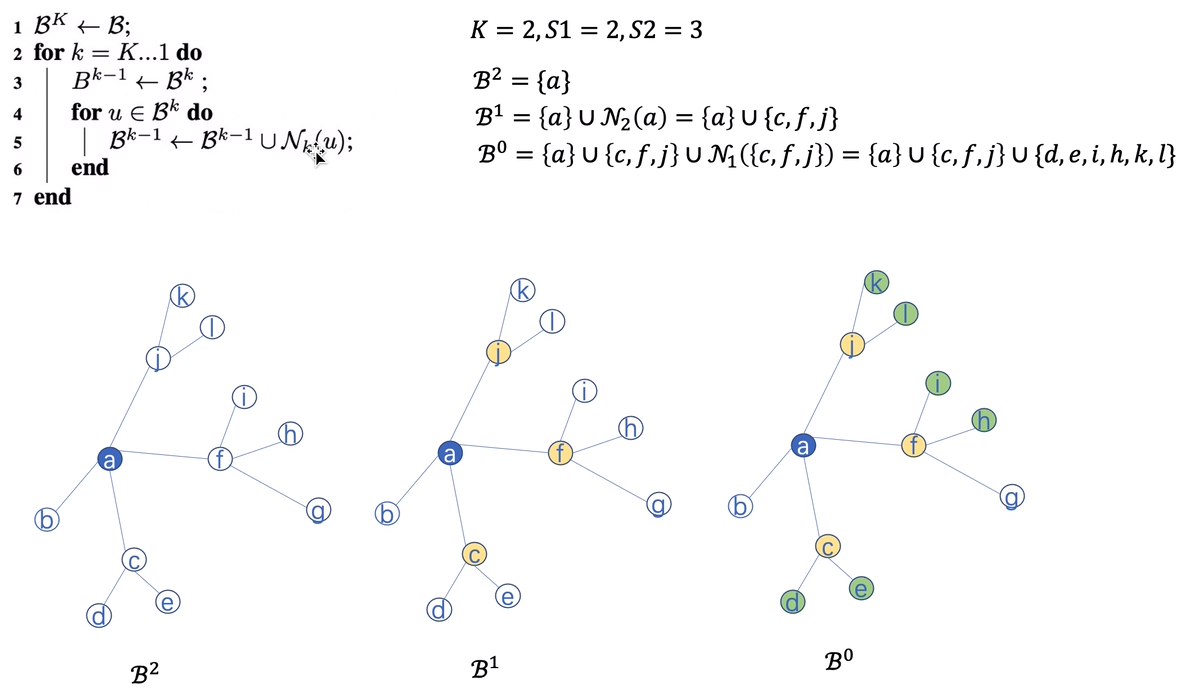
首先选定最后聚合到一起的节点，在上面的图中，最后想要聚集到的节点就是a节点。初始的指定的参数是K=2经过两层的居合，s1=2也就是在第一层的时候聚合2个节点，s2=3也就是在第二层的时候聚合三个节点。可以看见在b1也就是第二层的时候a随机选择了cfj三个节点进行聚合，在b0也就是第一层的时候cfj三个节点随机对2个邻居节点进行了聚合。

这样就可以将一张很大的图简化成只使用了以上的蓝色黄色绿色的三类点的小图

 图网络的分类

 

按照图计算的任务分类：节点问题(对节点进行分类)，输入边然后对边进行预测输出，对整个图进行分类匹配和生成。