pytorch——合并分割,数学运算，高级操作，神经元(激活函数)，损失函数

分割与合并

import torch
import numpy as np
#假设a是班级1-4的数据，每个班级里有32个学生，每个学生有8门分数
#假设b是班级5-9的数据，每个班级里有32个学生，每个学生有8门分数
#现在要将两个班级合并
a=torch.rand(4,32,8)
b=torch.rand(5,32,8)
c=torch.cat([a,b],dim=0) #在0维度上进行a和b的拼接.注意只有在拼接的维度上数字可以不一致
print(c.shape)

#使用stack拼接
c1=torch.rand(3,8)
d1=torch.rand(3,8)
cd=torch.stack([c1,d1],dim=0)
print('使用stack拼接',cd.shape) #在0维度进行拼接，会在前面插入多一个2的维度，
# 如果新生维度取0就是取上半部分，如果取1就是取下半部分
print('这里是c1',c1)
print('这里是d1',d1)
print('取上半部分',cd[0,0:,0:])
print('取上半部分',cd[1,0:,0:])

#拆分操作
#现在想吧(3,32,8)拆分成三个(1,32,8)
t1=torch.rand(3,32,8)
ts1,ts2,ts3=t1.split(1,dim=0) #将维度0拆分成每个都是1的
print(ts1.shape,ts2.shape,ts3.shape)
#现在想吧(3,32,8)拆分成两个(2,32,8)和(1,32,8)
ts1,ts2=t1.split([2,1],dim=0) #将维度0拆分成第一组两个，第二组1个
print(ts1.shape,ts2.shape)
#使用chunk按块的数量拆分
t1=torch.rand(6,32,8)
ts1,ts2,ts3=t1.chunk(3,dim=0) #将维度0拆分成3块
print(ts1.shape,ts2.shape,ts3.shape)

数学运算

#数学运算
a=torch.rand(3,4)
b=torch.rand(4)
print(a+b) #能执行成功是因为b会用自动拓展使得变成(1,4),然后变成(3,4)来和a运算
#print(a*b)
#print(a/b)
#print(a-b)

#矩阵相乘torch.matmul
a=torch.ones(3,3)
b=torch.tensor([[2,2,2],[2,2,2],[2,2,2]]).type(torch.float32)
print(torch.matmul(a,b))

#四维情况下的matmul,此时前两维度不变，取后两维做成矩阵然后进行乘积
a=torch.rand(4,3,28,64)
b=torch.rand(4,3,64,32)
print(torch.matmul(a,b).shape)

#有关于取值
qq=torch.tensor(3.14)
print('向下取',qq.floor(),'向上取',qq.ceil(),'取整数部分',qq.trunc(),'取小数部分',qq.frac())
print('四舍五入取整',qq.round())

#筛选
grad=torch.rand(2,3)*15
print(grad.max())
print(grad.median())
print(grad)
print(grad.clamp(9)) #小于9的变成9
print(grad.clamp(6,9)) #大于9的变成9，小于6的变成6

#求范数
f=torch.tensor([[2,2,2,2],[2,2,2,2]]).type(torch.float32)
print(f.norm(1),f.norm(2)) #可以加上dim指定某个维度求范数

#mean和prod和max和min 括号里面如果不加维度的参数会默认将所有维度打平成一个向量来求
m=torch.tensor([[0,1,2,3],[4,5,6,7]]).type(torch.float32)
print(m.shape)
#mean等于的是求和起来再除以size
print(m.mean())
#prod是乘积
print(m.prod())
#上面是打平来求的，下面来看不打平的
print('不打平的求后面这两个列的乘积',m.prod(1))
print('返回列的最大值的索引',m.argmax(1))

 高级操作

#keepdim用于求max或者argmax的时候，维度不改变，其他位置自动添加1
#topk，按顺序取几个大的
cd=torch.rand(2,3)
print('初始的tensor',cd)
print('取1维(针对前面的那一维也就是行)上最大的两个',cd.topk(2,dim=1))
#topk，按顺序取几个小的
cd=torch.rand(2,3)
print('初始的tensor',cd)
print('取1维(针对前面的那一维也就是行)上最小的两个',cd.topk(2,dim=1,largest=False))
#取第n个小的
cd=torch.rand(2,8)
print('初始的tensor',cd)
print('取1维(针对前面的那一维也就是行)上最小的第五个（第五小）',cd.kthvalue(5,dim=1))

# where把用其他两个tensort通过特定的条件生成一个tensor
cond=torch.tensor([[0.679,0.7271],[0.8884,0.4163]])
a=torch.tensor([[0.,0.],[0.,0.]])
b=torch.tensor([[1.,1.],[1.,1.]])
print(torch.where(cond>0.5,a,b))

神经元——激活函数

 

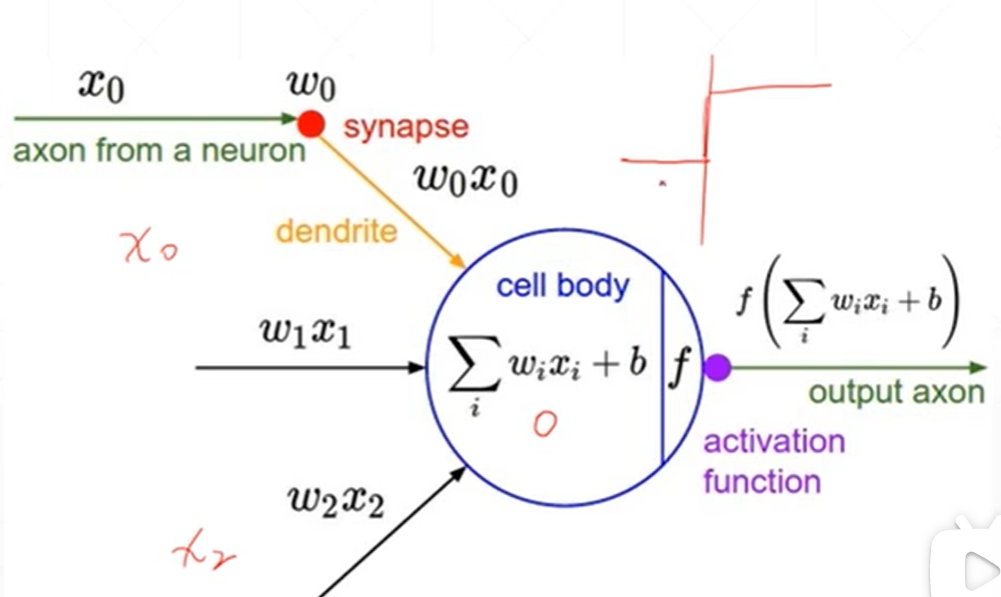
有x0到xi的多个输入，然后经过多个输入的ax+b的加权平均得到一个值，如果这个值大于阈值就可以做出反应，

而且这个反应的输出点平是定的，如果这个值不达到阈值就不会作出反应

为了弄可以求导的连续的提出了一种激活函数sigmoid（区间从0到1）

 

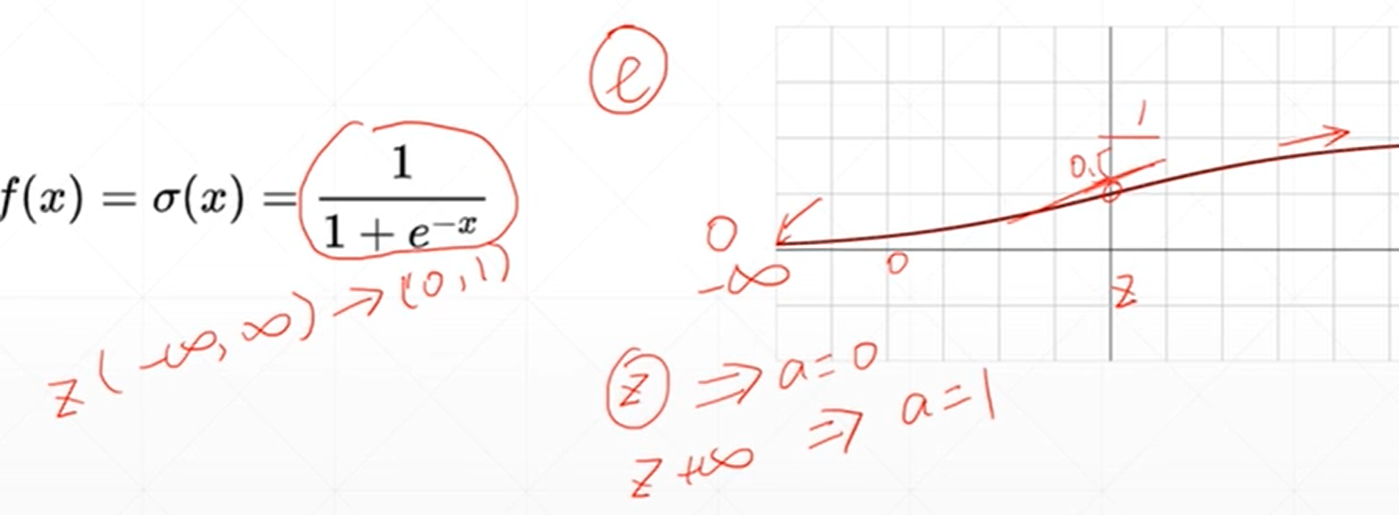
激活函数的导数

 

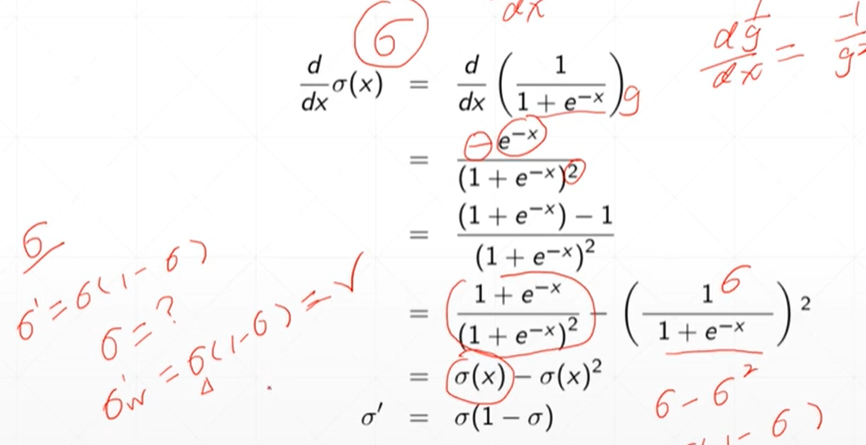
#调用sigmore函数
sig=torch.linspace(-100,100,10)
print(torch.sigmoid(sig))

另外一种的激活函数tanh(区间从-1到1)

tanh激活函数求得的导数的值

 

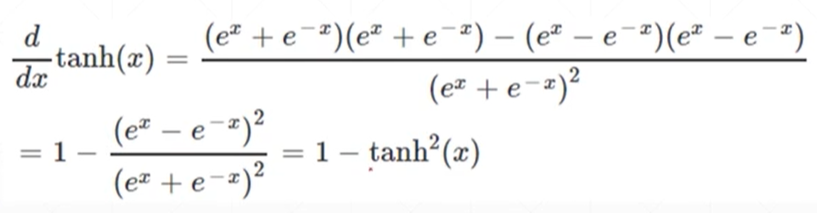
#调用tanh函数
tanh=torch.linspace(-3,3,5)
print(torch.tanh(tanh))

relu整形的线性单元

 

 

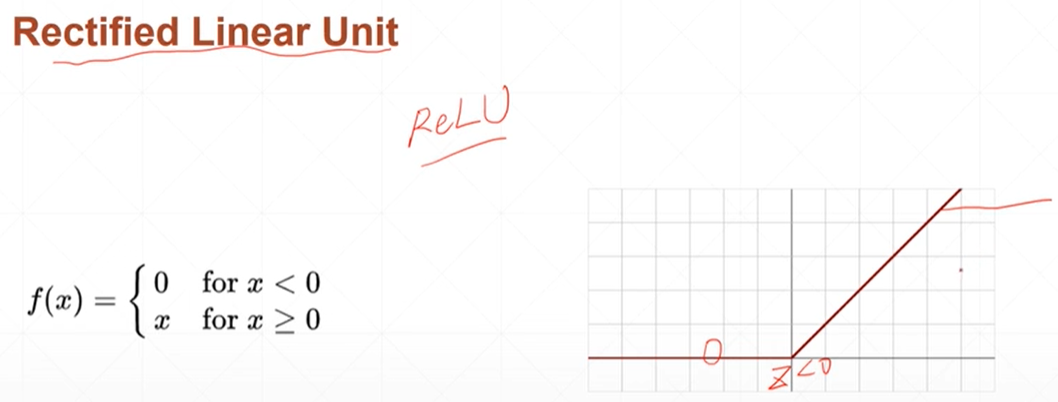
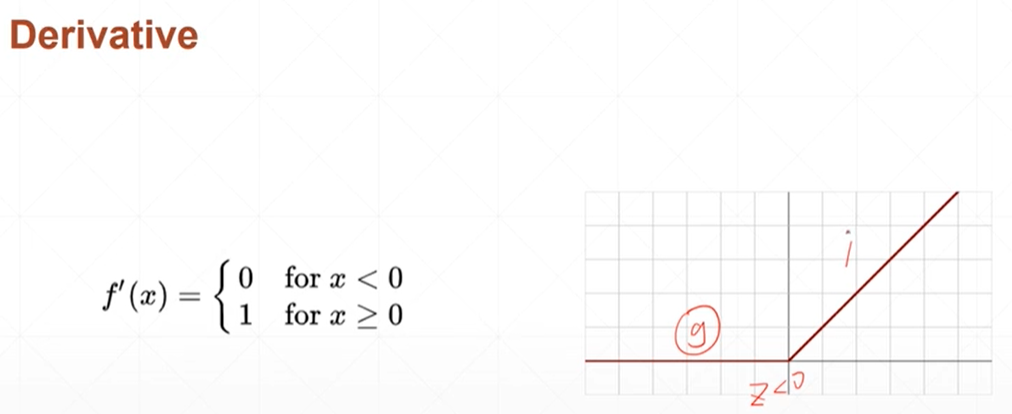
#调用relu函数
relu=torch.linspace(-3,3,5)
print(torch.relu(relu))

loss损失种类及其求导后的公式

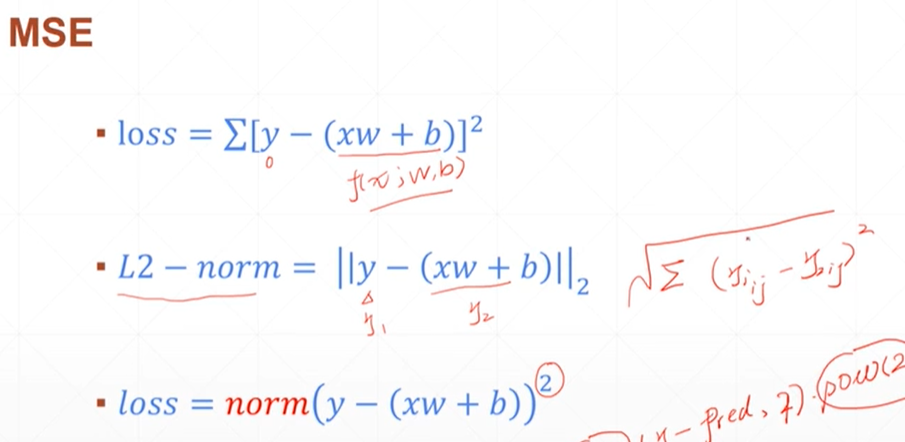
1.均方差

 均方差里面有两种，一种是loss还有一种是norm，norm相当于是对loss的开平方

import torch
x = torch.tensor([1]).type(torch.float32)   #x的值是单个数字1
x.requires_grad_()  #设置x是需要进行求导的
y = x*2 #公式
grads = torch.autograd.grad(outputs=y, inputs=x)[0]  #导数是output（y）去对input--x求导，由于y=2*1=2是标量，不是向量
#所以不用设置grad_outputs
print(grads)