题解 P4324 [JSOI2016]扭动的回文串

前置知识：

• 马拉车

• hash+二分求最长回文

首先，第一种贺第二种情况马拉车可以直接解决，在此不再赘述。

我们考虑第三种情况。

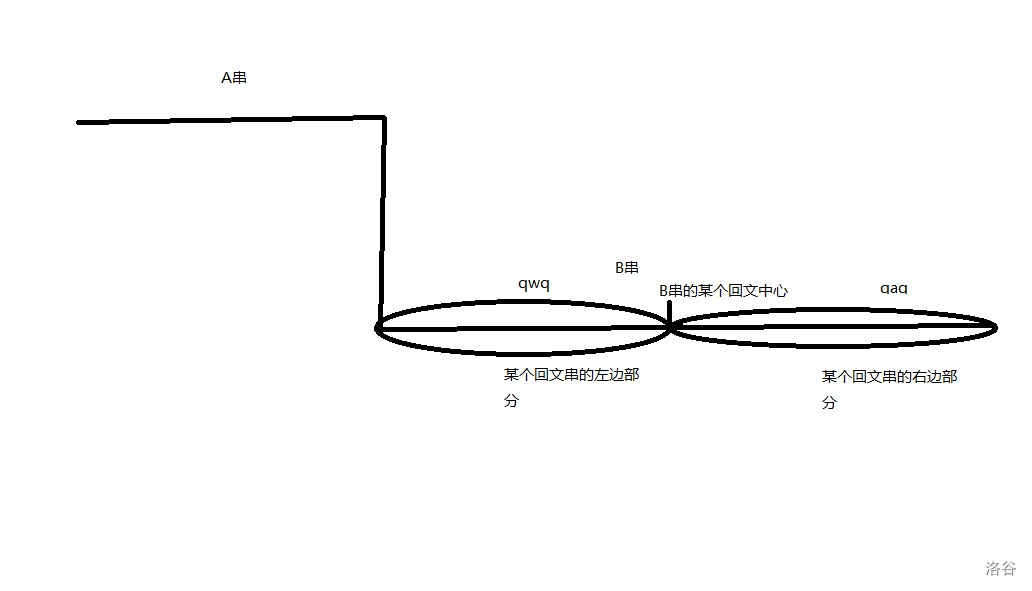
此时，\(\text{qwq}\) 与 \(\text{qaq}\) 必然是相等的，最后答案肯定是 \(\text{qwq}\) 向上扩展到 A串，然后 \(\text{qaq}\) 向右扩展。

Q：我们如何判断是否该向 A 串扩展了呢。

A：在B串中的回文串到头了就该连A了。举个例子，在这幅图中，假设以我画的那个点为回文中心，到 \(\text{qwq}\) 的边界就到头了。这个时候考虑将 \(\text{qwq}\) 向 A 串扩展，而 \(\text{qaq}\) 则向右扩展匹配回文。

因此，我们需要确定当前回文串最多可以扩展到哪里。然后从这个地方开始二分最多能扩展的长度。如果满足题意，计入答案。

但是，这只是其中一种情况。因为此时的回文中心可以在 A串，也可以在 B串。而且此时的回文串可以是奇回文，也可以是偶回文。

代码非常恶心，我们一部分一部分来。

第一部分：马拉车求前两种情况。

int init(char st[])
{

    int len=strlen(st);
    int j=2;
    s[0]='^';
    s[1]='#';
    for (int i=0;i<len;i++)
    {
        s[j++]=st[i];
        s[j++]='#';
    }
    s[j]='$';
    return j;
}
int manacher(char st[])
{
	int len=init(st);
	int mx=1;
	int k=1;
	int ans=-1;
	for(int i=1;i<len;i++)
	{
		if(i<mx) pp[i]=min(pp[2*k-i],mx-i);
		else pp[i]=1;
		while(s[pp[i]+i]==s[i-pp[i]]) pp[i]++;
		if(mx<i+pp[i])
		{
			mx=i+pp[i];
			k=i;
		}
		ans=max(ans,pp[i]-1);
	}
	return ans;
}

这个如果不会的话建议回去学马拉车。

第二部分：哈希

	for(int i=1;i<=n;i++)
	{
		h1[i]=h1[i-1]*rui+a[i];
		h2[i]=h2[i-1]*rui+b[i];
		p[i]=p[i-1]*rui;
	}
	for(int i=n;i>=1;i--)
	{
		hh[i]=hh[i+1]*rui+a[i];
	//	cout<<hh[i]<<endl;
		hh2[i]=hh2[i+1]*rui+b[i];
	}

这个不会的话建议重学字符串哈希。

第三部分：处理奇回文与偶回文的长度

这里需要二分答案。

我们枚举回文中心，然后对于每一个回文中心二分长度。

至于判定，只需要判定两边端点的 hash 值是否相等即可。

nt check(int now,int mid)
{
	if(h1[now]-h1[now-mid]*p[mid]==hh[now]-hh[now+mid]*p[mid]) return 1;
	else return 0;
}
int check2(int now,int mid)
{
	if(h1[now]-h1[now-mid]*p[mid]==hh[now+1]-hh[now+1+mid]*p[mid]) return 1;
	else return 0;
}
int check3(int now,int mid)
{
	if(h2[now]-h2[now-mid]*p[mid]==hh2[now]-hh2[now+mid]*p[mid]) return 1;
	else return 0;
}
int check4(int now,int mid)
{
	if(h2[now]-h2[now-mid]*p[mid]==hh2[now+1]-hh2[now+1+mid]*p[mid]) return 1;
	else return 0;
}
int check5(int nowl,int nowr,int mid)
{
	if(h1[nowl]-h1[nowl-mid]*p[mid]==hh2[nowr]-hh2[nowr+mid]*p[mid]) return 1;
	return 0;
}
int bs(int l,int r,int now)
{
	int mid;
	int best;
	while(l<=r)
	{
		mid=(l+r)/2;
		if(check(now,mid))
		{
			l=mid+1;
			best=mid;
		} 
		else r=mid-1;
	}
	return best;
}
int bs2(int l,int r,int now)
{
	int mid;
	int best;
	while(l<=r)
	{
		mid=(l+r)/2;
		if(check2(now,mid))
		{
			l=mid+1;
			best=mid;
		} 
		else r=mid-1;
	}
	return best;
}
int bss(int l,int r,int now)
{
	int mid;
	int best;
	while(l<=r)
	{
		mid=(l+r)/2;
		if(check3(now,mid))
		{
			l=mid+1;
			best=mid;
		} 
		else r=mid-1;
	}
	return best;
}
int bss2(int l,int r,int now)
{
	int mid;
	int best;
	while(l<=r)
	{
		mid=(l+r)/2;
		if(check4(now,mid))
		{
			l=mid+1;
			best=mid;
		} 
		else r=mid-1;
	}
	return best;
}

第四部分：确定端点，二分最大扩展长度。

首先，二分最大扩展长度其实是与前面的部分差不多的。因为我们只需要不停向外扩展，对于每一次扩展，判断是否回文即可。

当我们确定了最大扩展长度，与原回文串相加即可。

int check5(int nowl,int nowr,int mid)
{
	if(h1[nowl]-h1[nowl-mid]*p[mid]==hh2[nowr]-hh2[nowr+mid]*p[mid]) return 1;
	return 0;
}

int bss4(int l,int r,int nowl,int nowr)
{
	int mid;
	int best;
	while(l<=r)
	{
		mid=(l+r)/2;
		if(check5(nowl,nowr,mid))
		{
			l=mid+1;
			best=mid;
		} 
		else r=mid-1;
	}
	return best;
}
    

至此，这道题已经愉快的被你切了。