多项式题目
一些符号与约定
大写字母代表多项式,例如\(F\),\(G\)
\(f_i\) 则代表多项式\(F\) 的\(x^i\) 项的系数
SPOJ-SWERC14C, Golf Bot
description
有一个长为 \(N\) 的数组 \(k\) 与一个长为 \(M\) 的数组\(d\) ,求出 \(d\) 数组中能被 \(\le 2\) 个 \(k\) 数组中的数相加表示出来的数有多少个。(\(N,M,d_i,k_i\le 2\times 10^5\))
solution
同底数幂的乘法是指数相加系数相乘。这启示我们将\(k\) 放到指数上面。具体地,构造多项式\(F\) ,\(f_i=1\) 当且仅当\(i\) 出现在\(k\) 数组中。注意到不一定是由恰好两个数相加得到的,于是我们可以添加\(f_0=1\) 表示不选择。令\(G=F^2\) ,不难发现\(g_i>0\) 和\(i\) 能被表示出来是充分必要条件。于是直接\(FFT\) 即可。
code
#include<bits/stdc++.h>
using namespace std;
typedef double db;
const int N=8e5+5;const db pi=acos(-1.0),eps=1e-10;
struct cp{db x,y;};
inline cp operator+(const cp&x,const cp&y){return {x.x+y.x,x.y+y.y};}
inline cp operator-(const cp&x,const cp&y){return {x.x-y.x,x.y-y.y};}
inline cp operator*(const cp&x,const cp&y){return {x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
namespace Basis
{
int rev[N];cp wn[N],f[N],g[N];
inline void pre(int l,int lim)
{
for(int i=0;i<lim;++i)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
}
inline void FFT(cp*f,int lim,bool tp)
{
for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
wn[0]={1,0};cp g={cos(pi/mid),(tp?-1:1)*sin(pi/mid)};
for(int i=1;i<mid;++i)wn[i]=wn[i-1]*g;
int len=mid<<1;
for(int j=0;j<lim;j+=len)
for(int k=0;k<mid;++k)
{
cp x=f[j+k],y=f[j+mid+k]*wn[k];
f[j+k]=x+y,f[j+mid+k]=x-y;
}
}
if(tp)for(int i=0;i<lim;++i)f[i].x/=lim;
}
inline void mul(int n,int m,int*a,int*b)
{
int l=0,lim=1;while(lim<n+m)lim<<=1,++l;pre(l,lim);
for(int i=0;i<lim;++i)
f[i]={i<n?a[i]:0,0},g[i]={i<m?b[i]:0,0};
FFT(f,lim,0),FFT(g,lim,0);
for(int i=0;i<lim;++i)f[i]=f[i]*g[i];
FFT(f,lim,1);
}
}
int n,m,a[N],rub[N],cnt,mx,ans;
int main()
{
while(scanf("%d",&n)==1)
{
ans=mx=cnt=0;
for(int i=1,k;i<=n;++i)
scanf("%d",&k),a[k]=1,mx=max(rub[++cnt]=k,mx);
rub[++cnt]=0,a[0]=1;Basis::mul(mx+1,mx+1,a,a);
scanf("%d",&m);
for(int i=1,d;i<=m;++i)
scanf("%d",&d),ans+=d>2*mx?0:(Basis::f[d].x>eps);
printf("%d\n",ans);
for(int i=1;i<=cnt;++i)a[rub[i]]=0;
}
return 0;
}
UVA12298 Super Poker II
solution
考虑\(n=a_1+a_2+a_3+a_4\) 不难发现相当于从每种花色的牌中选出一种直接组合,这和多项式乘法的意义相同。
于是类似上一道题,我们构造\(F(x)=\sum_\limits i[i为合数]x^i\) 。如果某些牌不能选择,那么我们钦定其对应系数为\(0\) 。而后我们将四种花色代表的多项式乘起来得到多项式\(G\) 。\(g_i\) 就表示\(n=i\) 时的方案数,直接输出即可。
注意此题要开long double 。
code
#include<bits/stdc++.h>
using namespace std;
typedef long double db;
typedef long long ll;
const int N=1000000+5;const db pi=acos(-1.0),eps=1e-10;
struct cp{db x,y;};
inline cp operator+(const cp&x,const cp&y){return {x.x+y.x,x.y+y.y};}
inline cp operator-(const cp&x,const cp&y){return {x.x-y.x,x.y-y.y};}
inline cp operator*(const cp&x,const cp&y){return {x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
namespace Basis
{
int rev[N];cp wn[N],f[N],g[N];
inline void pre(int l,int lim)
{
for(int i=0;i<lim;++i)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
}
inline void FFT(cp*f,int lim,bool tp)
{
for(int i=0;i<lim;++i)if(i<rev[i])swap(f[i],f[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
wn[0]={1,0};cp g={cos(pi/mid),(tp?-1:1)*sin(pi/mid)};
for(int i=1;i<mid;++i)wn[i]=wn[i-1]*g;
int len=mid<<1;
for(int j=0;j<lim;j+=len)
for(int k=0;k<mid;++k)
{
cp x=f[j+k],y=f[j+mid+k]*wn[k];
f[j+k]=x+y,f[j+mid+k]=x-y;
}
}
if(tp)for(int i=0;i<lim;++i)f[i].x/=lim;
}
inline void mul(int n,int m,ll*a,ll*b,ll*ans)
{
int l=0,lim=1;while(lim<n+m)lim<<=1,++l;pre(l,lim);
for(int i=0;i<lim;++i)
f[i]={i<n?a[i]:0,0},g[i]={i<m?b[i]:0,0};
FFT(f,lim,0),FFT(g,lim,0);
for(int i=0;i<lim;++i)f[i]=f[i]*g[i];
FFT(f,lim,1);
for(int i=0;i<lim;++i)ans[i]=(ll)(f[i].x+0.1);
}
}
ll a[N],b[N],c[N],d[N],h[N];
bool flag[N];int pr[N],pcnt,n,m,k;
inline void init(int mx)
{
flag[1]=1;
for(int i=2;i<=mx;++i)
{
if(!flag[i])pr[++pcnt]=i;
for(int j=1;j<=pcnt;++j)
{
int num=pr[j]*i;if(num>mx)break;
flag[num]=1;if(i%pr[j]==0)break;
}
}
}
inline int get(char*ch,int len)
{
int s=0;
for(int i=0;i<len-1;++i)s=s*10+ch[i]-'0';
return s;
}
int main()
{
init(50000);
char opt[10];
while(scanf("%d%d%d",&n,&m,&k)&&n&&m)
{
for(int i=2;i<=m;++i)if(flag[i])a[i]=b[i]=c[i]=d[i]=1;
for(int i=1;i<=k;++i)
{
scanf("%s",opt);
int len=strlen(opt),num=get(opt,len);char t=opt[len-1];
if(t=='S')a[num]=0;
else if(t=='H')b[num]=0;
else if(t=='C')c[num]=0;
else d[num]=0;
}
Basis::mul(m+1,m+1,a,b,h);
Basis::mul(m+1,m+1,h,c,h);
Basis::mul(m+1,m+1,h,d,h);
for(int i=n;i<=m;++i)printf("%lld\n",h[i]);
puts("");
}
return 0;
}
UVA1718 Tile Cutting
solution
情况如图
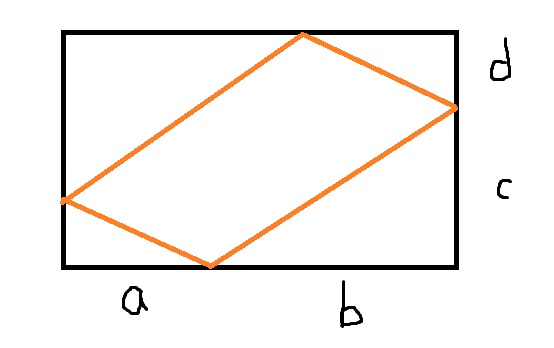
其中橙色平行四边形的面积为\((a+b)(c+d)-ad-bc=ac+bd=s\)
注意到\(s\) 是定值,因此相当于我们要求\(a,b,c,d\) 满足\(ac+bd=s\) 的方案数。
可以对于每个\(i\) 求出\(t_i=\sum_\limits{x,y}[xy=s]\) 。后面的就和前面的题相同了。构造多项式\(F(x)=\sum_\limits it_ix^i\) ,则\(G=F^2\) 的各项系数就分别对应该次数的方案数了。
Arithmetic Progressions, CodeChef COUNTARI(bzoj3509)
description
给定一个长度为\(n\) 的数组\(a\) ,求有多少个\(i,j,k\) 满足\(i<j<k\) 且\(a_k-a_j=a_j-a_i\)
data range
\(n\le 10^5,a_i\le 30000\)
solution
原式可以化为
于是可以考虑枚举\(j\) ,然后统计满足\(i<j<k\) 和上述条件的\((i,k)\) 数量。
不难想到多项式,设在\(j\) 左边数值\(t\) 出现了\(c_t\) 次,那么左侧的多项式为
右侧同理。左右两侧的多项式卷积起来后\(x^{2a_j}\) 的系数就是答案。
但是每次都这样乘复杂度显然爆炸,考虑优化。
运用分块的思想平衡复杂度,设块大小为\(B\) 。
对于每个块,都要进行一次如上的卷积,这部分的复杂度为\(\mathcal O(\frac nBmx\log_2mx)\) 其中\(mx=30000\)
然后我们需要遍历块中每一个下标作为\(j\) ,然后累加\(j\) 的所有块内贡献(块外贡献已经算出),这部分的复杂度为\(\mathcal O(nB)\)
根据均值不等式,当\(B=\sqrt{mx\log_2mx}\) 时最优,实际的话再微调就可以过了。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
typedef double db;
const db pi=acos(-1.0);
int mx;
struct cp{db x,y;};
inline cp operator+(const cp&x,const cp&y){return {x.x+y.x,x.y+y.y};}
inline cp operator-(const cp&x,const cp&y){return {x.x-y.x,x.y-y.y};}
inline cp operator*(const cp&x,const cp&y){return {x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
namespace Basis
{
int rev[N<<2],lim=1,l;cp wn[N<<2],a[N<<2],b[N<<2];ll t[N<<2];
inline void pre(int lim,int l)
{
for(int i=0;i<lim;++i)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
}
inline void fft(int lim,cp*f,bool tp)
{
for(int i=0;i<lim;++i)
if(i<rev[i])swap(f[i],f[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
wn[0]={1,0};cp g={cos(pi/mid),(tp?-1:1)*sin(pi/mid)};
for(int i=1;i<mid;++i)wn[i]=wn[i-1]*g;
int len=mid<<1;
for(int j=0;j<lim;j+=len)
for(int k=0;k<mid;++k)
{
cp x=f[j+k],y=f[j+mid+k]*wn[k];
f[j+k]=x+y,f[j+mid+k]=x-y;
}
}
}
inline void mul(int n,int m,int*f,int*g)
{
for(int i=0;i<lim;++i)
a[i].x=i<n?f[i]:0,b[i].x=i<m?g[i]:0,a[i].y=b[i].y=0;
fft(lim,a,0),fft(lim,b,0);
for(int i=0;i<lim;++i)a[i]=a[i]*b[i];
fft(lim,a,1);
for(int i=0;i<lim;++i)t[i]=(ll)(a[i].x/lim+0.1);
}
inline ll query(int pos){return t[pos];}
}
using namespace Basis;
int n,s[N],blk[N],lb[N],rb[N],cnt[N],f[N],g[N];ll ans;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d",s+i),mx=max(mx,s[i]);
int k=sqrt(n*log(mx)*0.9)+1;++mx;
for(int i=1;i<=n;++i)blk[i]=(i-1)/k+1,++g[s[i]];
for(int i=1;i<=blk[n];++i)
lb[i]=rb[i-1]+1,rb[i]=min(k*i,n);
while(lim<mx+mx)lim<<=1,++l;pre(lim,l);
for(int i=1;i<=blk[n];++i)
{
for(int j=lb[i];j<=rb[i];++j)--g[s[j]],++cnt[s[j]];
mul(mx,mx,f,g);
for(int j=lb[i];j<=rb[i];++j)
{
int now=s[j]<<1;
ans+=query(now);--cnt[s[j]];
for(int o=lb[i];o<j;++o)
if(now>=s[o])ans+=cnt[now-s[o]]+g[now-s[o]];
for(int o=j+1;o<=rb[i];++o)
if(now>=s[o])ans+=f[now-s[o]];
}
for(int j=lb[i];j<=rb[i];++j)++f[s[j]];
}
printf("%lld\n",ans);
return 0;
}
Unequalled Consumption, NWERC 2005, POJ2764
非常牛逼的一道题目呢。
solution
每种糖果的\(OGF\) 为
因此所有糖果合在一起的\(OGF\) 为
\(f_i\) 就表示要求总价值为\(i\) 时的糖果选取方案数。
但是这个东西是个分式,直接不好做。考虑化开,令\(W=lcm(w_1,w_2,\cdots,w_t)\) ,则
由等比数列求和公式\(\sum_\limits {i=l}^rx^i=x^l\cdot \dfrac{1-x^{r-l+1}}{1-x}\) ,因此
分为左右两半考虑。右边是一个多重背包:有\(n\) 种物品,每种物品价值为\(w_t\) 且有\(\frac{W}{{w_t}}-1\) 个。这个直接暴力做就可以了。设这个多项式为\(P\) ,其\(x^r\) 的系数为\(p_r\) .
再考虑左边的式子,其实只有\(x^0,x^W,x^{2W},\cdots\) 这些位置系数是非\(0\) 的。而不难发现\(x^{iW}\)其系数为\(\binom {n+i-1}{n-1}\) ,证明可以考虑隔板法,相当于将\(i\) 分到\(n\) 个盒子中去的方案数。设这个多项式为\(Q\) 。
现在假设我们要求总价值为\(m\) 时的方案数。不妨令\(m=kW+r\) ,那么我们有
上限为\(n-1\) 是因为\(P\) 的次数限制。
回到原问题,我们要求最小的\(m=kW+r\) 满足\(G(k,r)\ge P\) 。我们可以将\(m\) 按照其除以\(W\) 的余数进行分类,即我们每次固定\(r\) ,考虑所有除以\(W\) 余\(r\) 的\(m\) 的贡献。注意到此时\(G(k,r)\) 是随着\(k\) 增大而单调递增的,因此我们可以直接二分(可以从\(G(k+1,r)-G(k,r)>0\) 考虑证明这一结论)。至此问题解决。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号