二叉树

二叉树（Binary Tree) 是 n(n>=0) 个有限元素的集合。该集合或者为空，或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。

当集合为空时，称为空二叉树

图 1

二叉树特点

• 每个节点的度最大为 2 (最多拥有 2 颗子树)
  • 节点 A 的度为 2， 节点 E 的度为 0。
• 左子树和右子树有严格的顺序。
  • 如果将上图的节点 H 和 I 进行调换，则是一个完全不同的二叉树。
• 即使某个节点只有与一颗子树，也要区分是左子树还是右子树。
• 非空二叉树的第 i层，最多有 2^n-1 个节点(i >= 1)
  • 第二层(B C 层为第二层), 最多有 2 个节点，既 2^2-1 = 2
    
• 在高度为 h 的二叉树上最多有 2^h - 1 个节点 (h>=1)
  • 如果高度为 4 的二叉树，最多会有 2⁴ - 1 = 15个节点。
• 对于任何一颗飞空二叉树，如果叶子节点的个数为 n0 (度为0），度为 2 的结点个数为 n2，则有：n0 = n2 + 1
  • 上图中的 n0 为 5，n2 为 4。
• 假设度为 1 的节点个数为 n1 ，则有二叉树的节点总数 n = n0 + n1 + n2
• 二叉树的边数为 T = n - 1 也就是 T = n0 + n1 + n2 -1 也就是 T = 2 * n2 + n1

真二叉树(Proper Binary Tree)

所有节点的度要么为 0，要么为 2。

图1就是一颗真二叉树，节点的度都是 0 和 2。

满二叉树(Full Binary Tree)

所有节点的度要么为 0， 要么为 2，且所有叶子节点都在最后一层。

满二叉树

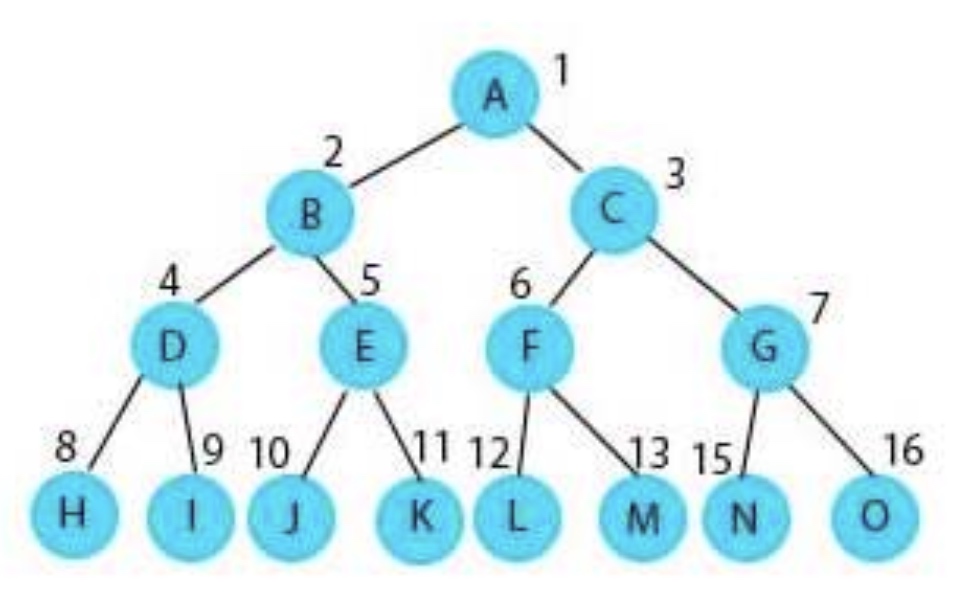
满二叉树 也是 真二叉树。两者的区别在于，满二叉树的叶子结点都在同一层。

完全二叉树

叶子节点在最后两层，且最后一层的叶子节点都靠左对齐。

完全二叉树

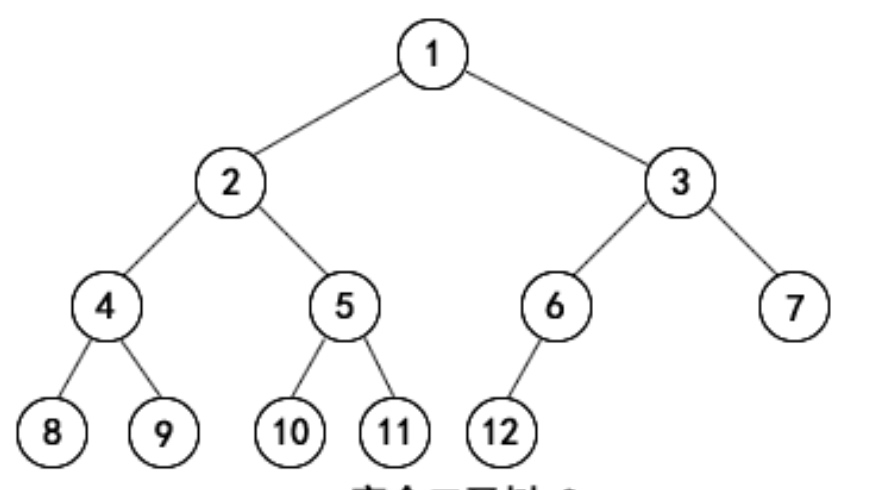
完全二叉树的特点：

• 完全二叉树度为 1 的节点，最多只能有 1 个。
• 假设一颗完全二叉树的高度为 h(h >= 1), 那么这颗二叉树至少有多少个节点？
  • 2^h-1 个节点
• 假设一颗完全二叉树的高度为 h(h >= 1), 那么这颗二叉树最多有多少个节点？
  • 2^h - 1 个节点
• 也就是说一颗完全二叉树的结点数 n : 2^h-1 <= n < 2^h

• 一颗有 n 个节点的完全二叉树（n > 0），从上到下、从左到右对节点从 1 开始编号，对任意第 i 个节点。则有：

  • 如果 i = 1 ，则是根节点
  • 如果 i > 1，则它的父节点编号为 i/2。
  • 如果 2i <= n ，则它的左子节点编号为 2i。完全二叉树的左子节点一定是偶数编号。
  • 如果 2i > n ，则该节点无左子节点。
  • 如果 2i + 1 <= n，它的右子几点编号为 2i + 1

• 思考一下，如果从 0 开始编号呢？