认识堆

堆的概念

堆实际上是一颗树，只不过在其基础上又加上新的性质，常见的堆有：二叉堆、二项堆、斐波那契堆等，其性质如下：

• 是一颗树，百度百科/维基百科上都说是一颗完全二叉树，但实际中二项堆并不是

• 父节点的值总是大于或等于（小于或等于）任何一个子节点的值，注意始终都没有说子节点之间的关系，也就是说子节点之间的关系并不重要

针对性质二又可以分为最大堆/大根堆与最小堆/小根堆，解释如下：

最大堆/大根堆：堆中的父节点的值总是大于等于它的子节点

最小堆/小根堆：堆中的父节点的值总是小于等于它的子节点

堆顶：二叉树的第一个节点称为根节点，而二叉堆称为堆顶

较为经常使用的是二叉堆，虽然通常说的堆结构即是指二叉堆，以至于两者的概念有点混淆，即使是百科也存在模糊不清，一会说是树又是完全二叉树？但我仍然还是想作一下区分，毕竟堆中还有其他的数据结构，而其数据结构必然符合堆的性质，所以我认为堆是一棵树！

二叉堆

二叉堆是一颗完全二叉树，对于完全二叉树的定义可参看之前的文章。二叉堆的存储结构一般用数组来表示，假设某一个节点的索引为：N，其左节点的索引应为：2N + 1，其右子节点的索引为：2N + 2，如下所示:

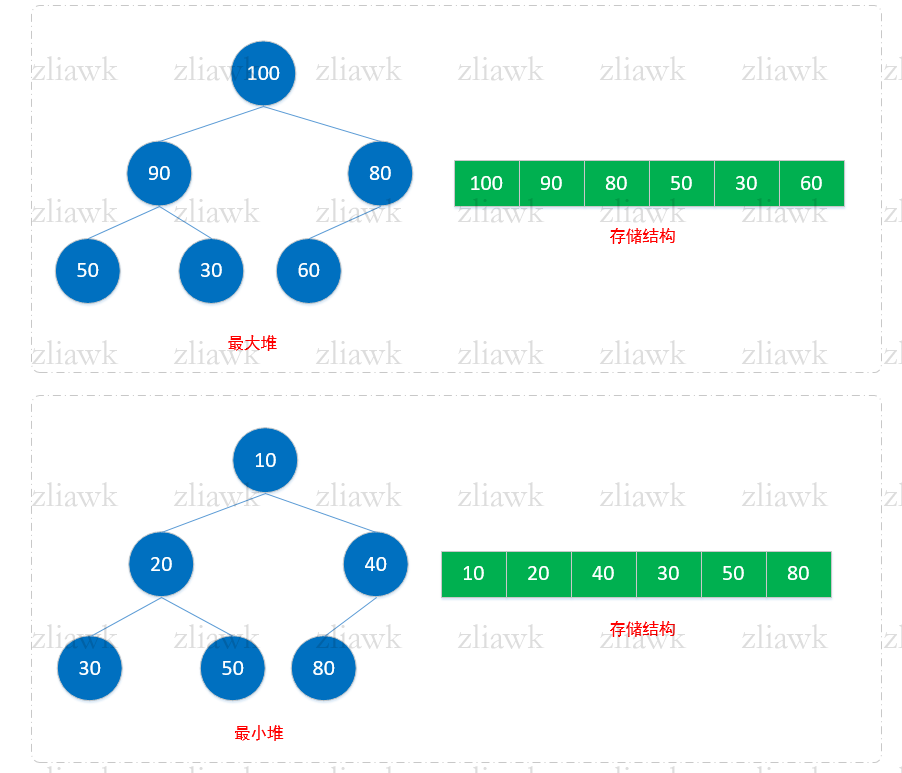
发现没有，它是按照二叉树的前序方式排列到数组中，所谓前序简单来说就是父节点放第一个，中序就是父节点放中间，后序自然就是父节点放最后一个了。还有一点需要注意下，二叉堆中并未要求左右子节点的值大小要求，也可以将值理解成优先级，对于最大堆来说，认为值越大说明优先级越高，位置更靠前，而对于最小堆来说，认定值越小优先级越高，这就看需要了！对于二叉树来说，通常左节点的值要比父节点小，而右子节点的值要比父节点大，但对于二叉堆来说，左右节点的值要么是大于等于父节点的值要么是小于等于。

二项堆

二项堆是二项树的集合，简单来说，就是在二项树的基础上加上了其他性质，二项树的性质如下：

• 高/深度为K的树，根节点下有K个子节点，每个子节点的高/深度分别是K-1、K-2、...2、1、0

• 高/深度为K的树，共有有2^K-1个节点，百科中认为高/深度是从0开始算起，有些书籍是从1开始算起，因为之前有关树的介绍文章中也是1，故而还是按照以前的说法！

接下来说说二项堆的性质：

• 每颗二项树都是最小堆，即父节点的值总是小于等于它的子节点

• 不能有两颗或以上的二项树有相同的高/深度，换句话说，具有高/深度的二项树有0或1个

与二叉堆相比，其优势是可以快速合并两个堆，一般使用链表作为其存储结构，由于过于复杂直接引用了网上的图片，如下图所示：

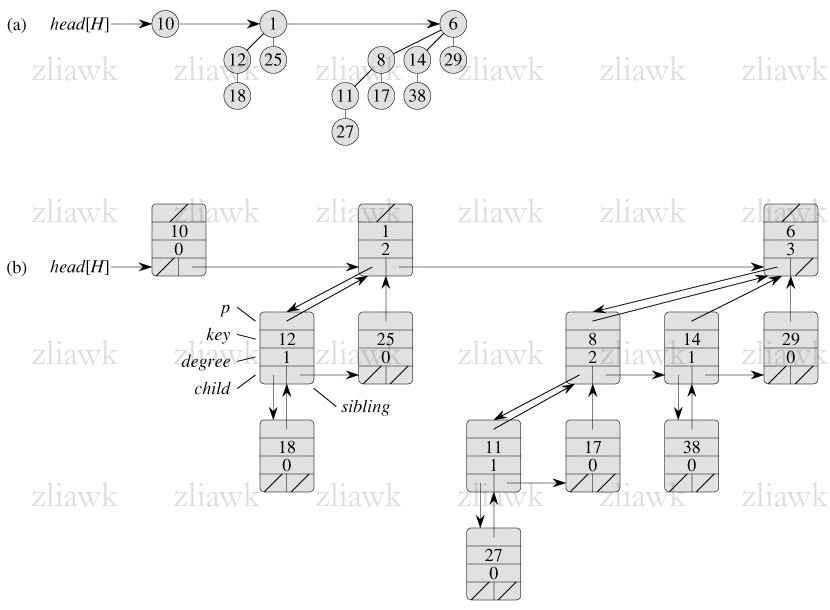
斐波那契堆

网上资料，包括百科都解释地稀里糊涂，各种语言实现，我想说能先把概念描述清楚了在谈其他吗？基本上每篇文章都是照搬《算法导论》的知识点，我没看过这本书，所以不敢往下结论，只是在这里告诉读者有这么一种类型的堆！顺便附上网上引用的关于其存储结构的图片，如下图所示：

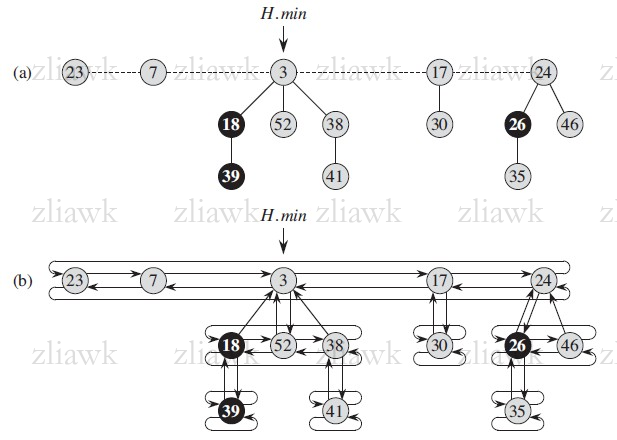
二叉堆的设计与实现

尝试手写了二叉堆，因为其较为常用，剩下两种数据结构比较难，对于基础不好或是不感兴趣的读者建议绕开！有兴趣的同学可以去github上观摩-二叉堆设计

总结

笔者也是第一次接触到关于堆的概念，所以此篇文章更多的是帮助读者去认识它！若有讲解不到位的地方欢迎指出，将积极改正。