二分图

基础知识：

定义：G=（V，E）的无向图，顶点V分在两个子集（A，B）里，每条边（i，j）关联的两个顶点分别属于A，B两个顶点集如果存在这样的划分，则此图为一个二分图，如下图所示的六个图全都是二分图：

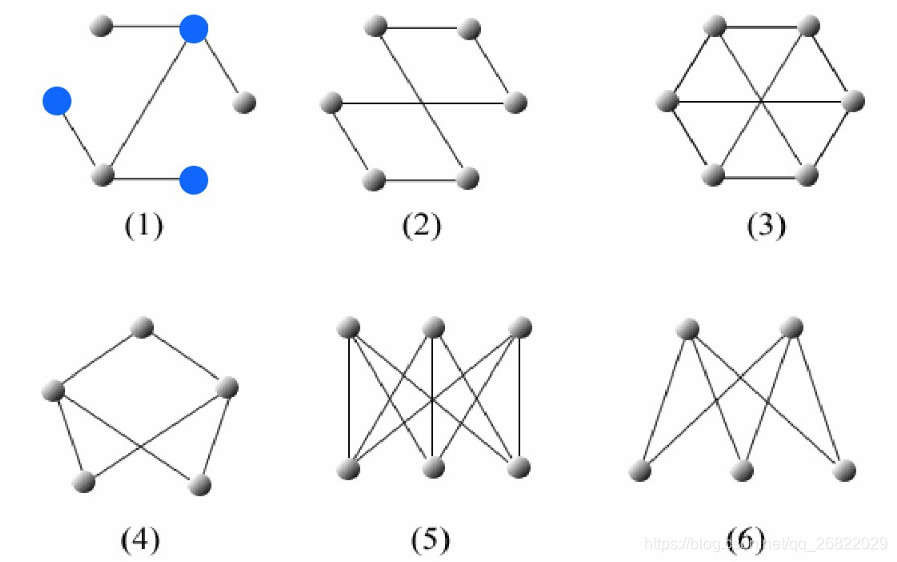
定理：G为二部图的充要条件是G中的每一个圈的长度都是偶数。

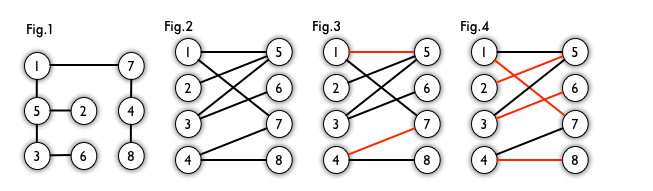
匹配：设G=<V, E>是二分图，而且E是V1和V2的笛卡尔乘积子集。若M包含于E，而且M中任何两条边不相邻，则称M是G的一个匹配；

最大匹配： 具有边数量最多的匹配称为最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配： 若|V1|=|V2|=|M|，则称M为完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

杆：匹配M中的边e。

最大独立集=顶点数-最大匹配数

最小边覆盖=最大匹配数+顶点数数-2*最大匹配=顶点数-最大匹配数

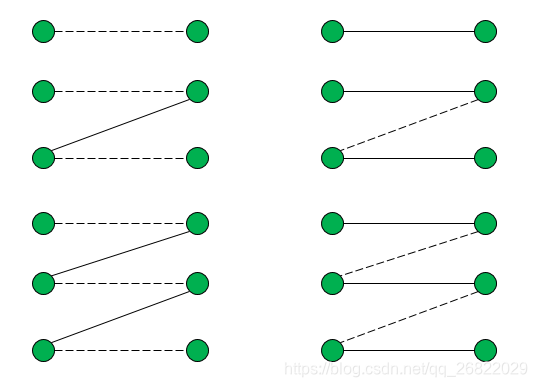
下图中左边的路都是交错路，也是增广路，其端点都是非饱和点，实线所表示的边都是匹配中的边。如果我们像右边的图那样，将左边路中的实线变成虚线边，将虚线边变成实线边就可以逐步增加匹配中的边，从而使得匹配达到最大匹配。接下来介绍的求最大匹配的算法就是基于这种思想。

匈牙利算法（没有权值）

解决目标：最大匹配

基本思想： 通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（增广路定理）。

基本步骤：

任取一匹配M (可以是空集或者只含有一条边的集合）；
令S = {u|u∈V1∩u是M的非饱和点}，若S为空集，则M已经是最大匹配，exit;
否则，S不为空，任取一非饱和点u0作为起点，从此起点走出几条交错路 Pil， Pi2,…；
如果它们中有某条路P是增广路（即P的终点也是非饱和点），则令M(M\P)U(P\M)(并且满足|M| (新)=|M| (旧)+1)，回到No 3;
否则，如果它们中无一条是增广路（即终点全是饱和点），则令S=S{u0}。如果S不为空，则回到No3; 否则S为空，则M就是最大匹配，exit

匈牙利算法板子：

int find(int x)
{
	for(int i=1;i<=n;i++) //扫描
    {
		if (a[x][i]==1&& vis[i]==0)//如果图中相连并且还没有标记过
		{
			vis[i]=1;
			if (d[i]==-1 || find(d[i])) //能腾位置，使用递归
			{d[i]=x;return 1;}
		}
	}
	return 0;
}

主函数中调用方法：
    
for (i=1;i<=n;i++)
{
	memset(used,0,sizeof(used));    //这个在每一步中清空
	if find(i) all+=1;
}

判断是否为二分图板子：

dfs：

bool judge(int v, int w)//染色法判断是否是二分图
{
    color[v] = w;    //将当前顶点涂色
    for(int i = 1; i <=n; i++){    //遍历所有相邻顶点，即连着的点
        if(a[v][i] == 1){    //如果顶点存在
            if(color[i] == w)    //如果颜色重复，就返回false
                return false;
            if(color[i] == 0 && !judge(i,-w))    //如果还未涂色，就染上相反的颜色-c,并dfs这个顶点，进入下一层
                return false;   //返回false
        }
    }
    return true;   //如果所有顶点涂完色，并且没有出现同色的相邻顶点，就返回true
}

bfs：

const int maxn = 1e5+10;
vector <int> G[maxn];
int col[maxn];
bool bfs(int u)//这里因为不一定连通图的原因设置一个变量，外部引用函数的时候遍历访问就行
{
    queue<int> q;
    q.push(u);//当前点入队
    col[u]=1;//当前点涂色
    while(!q.empty())
    {
        int v=q.front();
        q.pop();
        for(int i=0;i<G[v].size();i++)//遍历与当前点关联的所有点
        {
            int x=G[v][i];//获得第i个关联点的下标
            if(col[x]==0)//如果没图色
            {
                col[x]=-col[v];//图相反颜色
                q.push(x);
            }
            else
            {
                if(col[x]==col[v])//颜色相同不是二分图返回false
                    return false;
            }
        }
    }
    return true;
}

void solve()
{
    for(int i=1;i<=n;i++)
    {
       if(col[i]==0&&!bfs(i))
       {
           printf("No\n");
           return;
       }
    }
    printf("Yes\n");
}

例题1

匈牙利算法板子题求最大匹配

过山车 HDU - 2063

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1e3+5;
int k,m,n,x,y,cnt,a[maxn][maxn],d[maxn],vis[maxn];
int find(int x)
{
	for(int i=1;i<=n;i++) //扫描
    {
		if (a[x][i]==1&& vis[i]==0)//如果相连并且还没有标记过
		{
			vis[i]=1;
			if (d[i]==-1 || find(d[i])) //能腾位置，使用递归
			{d[i]=x;return 1;}
		}
	}
	return 0;
}
int main()
{
    while(cin>>k)
    {
        //cout<<k<<"****"<<endl;
        if(k==0)break;
        memset(a,0,sizeof(a));
        memset(d,-1,sizeof(d));
        cnt=0;
        cin>>m>>n;
        //cout<<m<<"***"<<n<<endl;
        while(k--)
        {
            cin>>x>>y;
            a[x][y]=1;
        }
        for(int i=1;i<=m;i++)
        {
            memset(vis,0,sizeof(vis));
            if(find(i))cnt++;
        }
        cout<<cnt<<endl;
    }
    return 0;
}

例题二

匈牙利算法板子题先判断是否为二分图再求最大匹配

The Accomodation of StudentsHDU - 2444

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=505;
int k,n,r,c,cnt,a[maxn][maxn],d[maxn],vis[maxn],color[maxn];
int find(int x)
{
	for(int i=1;i<=n;i++) //扫描
    {
		if (a[x][i]==1&& vis[i]==0)//如果相连并且还没有标记过
		{
			vis[i]=1;
			if (d[i]==-1 || find(d[i])) //能腾位置，使用递归
			{d[i]=x;return 1;}
		}
	}
	return 0;
}
bool judge(int v, int w)//染色法判断是否是二分图
{
    color[v] = w;    //将当前顶点涂色
    for(int i = 1; i <=n; i++){    //遍历所有相邻顶点，即连着的点
        if(a[v][i] == 1){    //如果顶点存在
            if(color[i] == w)    //如果颜色重复，就返回false
                return false;
            if(color[i] == 0 && !judge(i,-w))    //如果还未涂色，就染上相反的颜色-c,并dfs这个顶点，进入下一层
                return false;   //返回false
        }
    }
    return true;   //如果所有顶点涂完色，并且没有出现同色的相邻顶点，就返回true
}

int main()
{
    while(cin>>n>>k)
    {
        memset(a,0,sizeof(a));
        memset(d,-1,sizeof(d));
        memset(color,0,sizeof(color));
        cnt=0;
        while(k--){cin>>r>>c;a[r][c]=1;}
        if(!judge(1,1)){cout<<"No"<<endl;continue;}
        for(int i=1;i<=n;i++)
        {
            memset(vis,0,sizeof(vis));
            if(find(i))cnt++;
        }
        cout<<cnt<<endl;
    }
    return 0;
}

例题三

给一堆相互认识的人的标号，人数的人数和哪些人，求最多有几人都相互不认识，就是最大独立集问题

Girls and Boys

HDU - 1068

给一堆相互认识的人的标号，人数的人数和哪些人，求最多有几人都相互不认识，就是最大独立集问题

**最大独立集**=顶点集-最大匹配数

**最小边覆盖**=最大匹配+点数-2*最大匹配=点数-二分图的最大匹配

所以在一般板子的基础上对最后的结果处理一下

ans=n-ans/2；

#include<iostream>
#include<cstring>
using namespace std;
const int maxn=505;
int k,n,x,y,cnt,a[maxn][maxn],d[maxn],vis[maxn];
int find(int x)
{
	for(int i=0;i<n;i++) //扫描
    {
		if (a[x][i]==1&& vis[i]==0)//如果相连并且还没有标记过
		{
			vis[i]=1;
			if (d[i]==-1 || find(d[i])) 	{d[i]=x;return 1;}//能腾位置，使用递归
		}
	}
	return 0;
}

int main()
{
    while(cin>>n)
    {
        memset(a,0,sizeof(a));
        memset(d,-1,sizeof(d));
        cnt=0;
        for(int i=0;i<n;i++)
        {
            scanf("%d: (%d) ",&x,&k);
            while(k--)
            {cin>>y;a[x][y]=1;}
        }
        for(int i=0;i<n;i++)
        {
            memset(vis,0,sizeof(vis));
            if(find(i))cnt++;
        }
        cout<<n-cnt/2<<endl;
    }
    return 0;
}

KM算法（有权值）

解决目标：最大或者最小权匹配（最佳匹配）

基本思想： 基本思想是通过引入顶标，将最优权值匹配转化为最大匹配问题。。（只要会求最大匹配，如果要求最小权匹配，则将权值取相反数，再把结果取相反数，那么最小权匹配就求出来了。）

基本步骤:

初始化可行顶标的值；
用匈牙利算法寻找完备匹配；
若未找到完备匹配则修改可行顶标的值；
重复（2）（3）直到找到相等子图的完备匹配为止。

posted @ 2020-08-03 13:28 神奇周一阅读(255) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

神奇周一

二分图

二分图