torch.nn.KLDivLoss

KL散度

KL散度，又叫相对熵，用于衡量两个分布之间的距离。设$p(x),q(x)$是关于随机变量$x$的两个分布，则$p$相对于$q$的KL散度为：

• 信息论中，熵$H(P)$表示对来自$P$的随机变量进行编码所需的最小字节数，
• 而交叉熵$H(P,Q)$则表示使用基于$Q$的编码对来自$P$的变量进行编码所需的字节数，它也可以作为损失函数，即交叉熵损失函数，

•  因此，KL散度可以认为是使用基于$Q$的编码对来自$P$的变量进行编码所需的“额外”字节数；显然，额外字节数必然非负，当且仅当$P=Q$时，额外字节数为0，

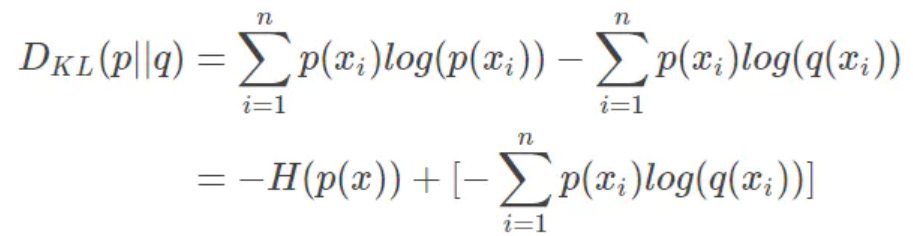等式的前一部分恰巧就是$P$的熵，等式的后一部分，就是交叉熵,

CLASS torch.nn.KLDivLoss(size_average=None, reduce=None, 
reduction='mean', log_target=False)

The Kullback-Leibler divergence loss.

For tensors of the same shape $y_{\text{pred}},\ y_{\text{true}}$，where $y_{\text{pred}}$  is the input and $y_{\text{true}}$ is the target，we define the pointwise KL-divergence as

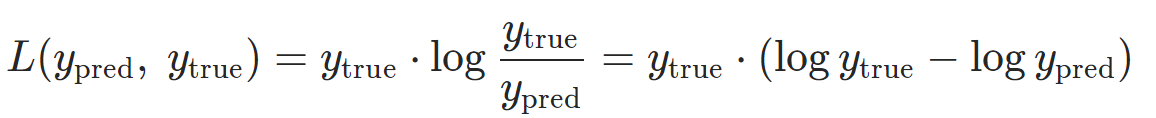
To avoid underflow(下溢) issues when computing this quantity, this loss expects the argument input in the log-space. The argument target may also be provided in the log-space if log_target= True.

To summarise, this function is roughly equivalent to computing

if not log_target: # default
    loss_pointwise = target * (target.log() - input)
else:
    loss_pointwise = target.exp() * (target - input)

and then reducing this result depending on the argument reduction as

if reduction == "mean":  # default
    loss = loss_pointwise.mean()
elif reduction == "batchmean":  # mathematically correct
    loss = loss_pointwise.sum() / input.size(0)
elif reduction == "sum":
    loss = loss_pointwise.sum()
else:  # reduction == "none"
    loss = loss_pointwise

reduction= “mean” doesn’t return the true KL divergence value, please use reduction= “batchmean” which aligns with the mathematical definition. In a future release, “mean” will be changed to be the same as “batchmean”.

参数：

• size_average，reduce Deprecated (see reduction)　

• reduction (string, optional) – Specifies the reduction to apply to the output. Default: “mean”

• log_target (bool, optional) – Specifies whether target is the log space. Default: False

Shape:

• Input: (*), where * means any number of dimensions. 
• Target: (*), same shape as the input. 
• Output:
  • scalar by default.
  • If reduction is ‘none’, then (*), same shape as the input.

kl_loss = nn.KLDivLoss(reduction="batchmean")
# input should be a distribution in the log space
input = F.log_softmax(torch.randn(3, 5, requires_grad=True))
# Sample a batch of distributions. Usually this would come from the dataset
target = F.softmax(torch.rand(3, 5))
output = kl_loss(input, target)

kl_loss = nn.KLDivLoss(reduction="batchmean", log_target=True)
log_target = F.log_softmax(torch.rand(3, 5))
output = kl_loss(input, log_target)