85. 最大矩形
目录:
题目
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例 1:
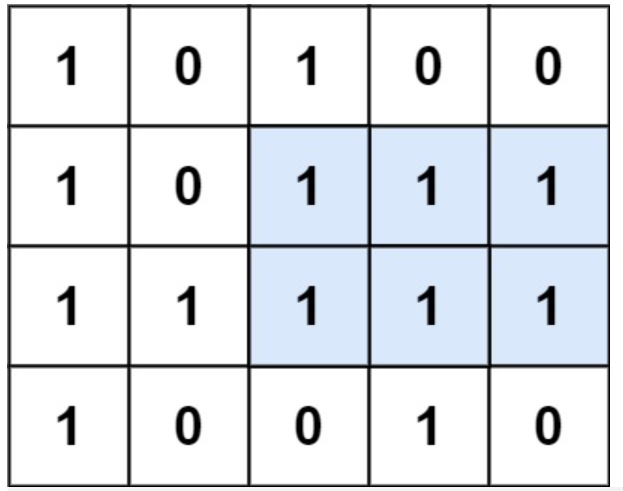
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
解释:最大矩形如上图所示。
示例 2:
输入:matrix = []
输出:0
示例 3:
输入:matrix = [["0"]]
输出:0
示例 4:
示例 5:输入:matrix = [["1"]]
输出:1
输入:matrix = [["0","0"]]
输出:0
提示:
- rows == matrix.length
- cols == matrix[0].length
- 1 <= row, cols <= 200
- matrix[i][j] 为 '0' 或 '1'
单调栈法
每一层看作是柱状图,可以套用84题柱状图的最大面积的单调栈法。
- 第一层柱状图的高度["1","0","1","0","0"],最大面积为1;
- 第二层柱状图的高度["2","0","2","1","1"],最大面积为3;
- 第三层柱状图的高度["3","1","3","2","2"],最大面积为6;
- 第四层柱状图的高度["4","0","0","3","0"],最大面积为4;
class Solution {
public int maximalRectangle(char[][] matrix) {
if(matrix.length==0 || matrix[0].length==0)
return 0;
int ret = 0;
int row = matrix.length;
int col = matrix[0].length;
int[] heights = new int[col];
for(int i = 0;i<row;i++)
{
for(int j = 0;j<col;j++)
{
/**
*求当前第i行往上连续1的个数,不连续就置为0
* 高度必须从底部起开始算起
* heights是逐行更新,当前行的更新是在上一行结果
* 的基础上进行的
*/
if(matrix[i][j]=='1')
heights[j]+=1;
else//一票否决
heights[j] = 0;
}
ret = Math.max(ret,largestRectangleArea(heights));
}
return ret;
}
/**
* 84. 柱状图中最大的矩形
*/
public int largestRectangleArea(int[] heights) {
Deque<Integer> stk = new ArrayDeque<>();
int area = 0,n = heights.length;
for(int i = 0; i < n; ++i) {
while(!stk.isEmpty() && heights[i] < heights[stk.peek()]) {
int h = heights[stk.peek()];
stk.pop();
int w = stk.isEmpty() ? i : i-1-stk.peek();
area = Math.max(h * w, area);
}
stk.push(i);
}
while(!stk.isEmpty()) {
int h = heights[stk.peek()];
stk.pop();
int w = stk.isEmpty() ? n : n-1-stk.peek();
area = Math.max(h * w, area);
}
return area;
}
}
动态规划法
- 循环遍历以(i,j)为右下角的最大矩形面积
- 辅助数组dp的含义:
-
- dp[i][j][0]:以(i,j)为起点,向左连续1的个数
-
- dp[i][j][1]:以(i,j)为起点,向上连续1的个数
class Solution {
public int maximalRectangle(char[][] matrix) {
if (matrix.length == 0 || matrix[0].length==0)
return 0;
int m = matrix.length;
int n = matrix[0].length;
int ret=0;
/*
* 0-> width
* 1-> height
*/
int[][][] dp = new int[m][n][2];
//左上角
if(matrix[0][0]=='1')
{
dp[0][0][0]=1;
dp[0][0][1]=1;
ret = 1;
}
//第一行
for(int j = 1;j < n;j++)
{
if(matrix[0][j]=='1')
{
dp[0][j][0] = dp[0][j-1][0]+1;
dp[0][j][1] = 1;
ret = Math.max(ret,dp[0][j][0]);
}
}
//第一列
for(int i=1;i<m;i++)
{
if(matrix[i][0]=='1')
{
dp[i][0][0]=1;
dp[i][0][1]=dp[i-1][0][1]+1;
ret=Math.max(ret,dp[i][0][1]);
}
}
//其他(i,j)
for(int i = 1;i < m;i++)
{
for(int j = 1;j < n;j++)
{
if(matrix[i][j]=='1')
{
dp[i][j][0]=dp[i][j-1][0]+1;
dp[i][j][1]=dp[i-1][j][1]+1;
int width=dp[i][j][0];
int height=dp[i][j][1];
int minHeight=height;
/*
* 遍历以(i,j)为右下角、宽度为k所能构成的
* 的矩形面积
*/
for(int k = 1;k <= width;k++)
{
/*
*此时所能构成的矩形的高度为以k为宽度的所有立柱
*中从底部起的1的连续值的最小值,由于我们是逐渐增加
*宽度的,所以当前的最小值等于新增加的一列的值和之前
* 的最小值的最小值
*/
minHeight=Math.min(minHeight,dp[i][j-k+1][1]);
ret=Math.max(ret,k*minHeight);
}
}
}
}
return ret;
}
}
动态规划方法的另一种实现:
- dp[i][j]为以(i,j)为起始点向上连续1的个数
- 至于以(i,j)为起始点向左连续1的个数我们可以k <= j+1 && matrix[i][j-k+1]!='0';代替
class Solution{
public int maximalRectangle(char[][] matrix)
{
int m = matrix.length, n = matrix[0].length;
int ret = 0;
// dp[i][j]为以(i,j)为起始点向上连续1的个数
int[][] dp = new int[m][n];
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(matrix[i][j] == '0')
continue;
if(i==0)
dp[i][j] = 1;
else
dp[i][j] = dp[i-1][j] + 1;
int minHeight = dp[i][j];
for(int k = 1; k <= j+1 && matrix[i][j-k+1]!='0'; k++)
{
minHeight=Math.min(minHeight,dp[i][j-k+1]);
ret=Math.max(ret,k*minHeight);
}
}
}
return ret;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号