LightGBM及其工具库实际使用
前言
LightGBM,2017年由微软提出,是GBDT模型的另一个进化版本,主要用于解决GBDT在海量数据中遇到的问题,以便更好更快的用于工业实践中。
从LightGBM名字我们可以看出其是轻量级(Light)的梯度提升机(GBM),LightGBM在xgboost的基础上进行了很多的优化,可以看成是XGBoost的升级加强版,它延续了xgboost的那一套集成学习的方式,但是它更加关注模型的训练速度,相对于xgboost,具有训练速度快和内存占用率低的特点。
下图分别显示了 XGBoost、XGBoost_hist(利用梯度直方图的 XGBoost) 和 LightGBM 三者之间针对不同数据集情况下的内存和训练时间的对比:
- 速度更快
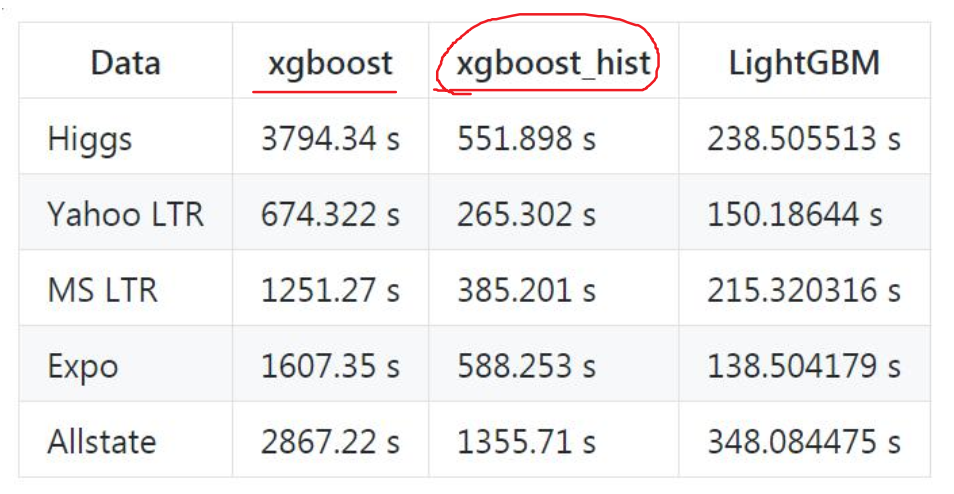
- 内存占用更低
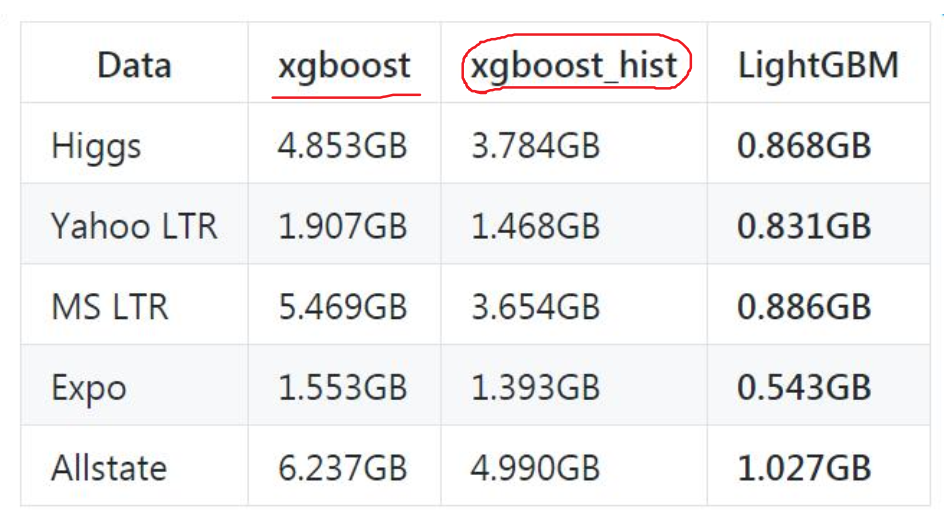
- 准确率更高(优势不明显, 与XGBoost相当)
本文主要关注于LightGBM到底是做了哪些方面的优化改进,才做到更快的训练速度和更低的内存使用的,以及LightGBM工具库的使用。
LightGBM的优化改进
直方图算法
直方图算法
LightGBM的直方图算法是代替Xgboost的预排序算法的,虽然直方图的算法思路不算是Lightgbm的亮点,毕竟xgboost里面的近似算法也是用的这种思想,但是这种思路对于xgboost的预排序本身也是一种优化,所以Lightgbm本着快的原则,也采用了这种直方图的思想。
那么LightGBM里面的直方图算法究竟在做什么事情呢?
LightGBM的直方图算法的基本思想就是,
- 把连续的浮点特征值离散化为k个整数(也就是分桶bins的思想),
- 同时构造一个宽度为k的直方图。
- 在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,
- 当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
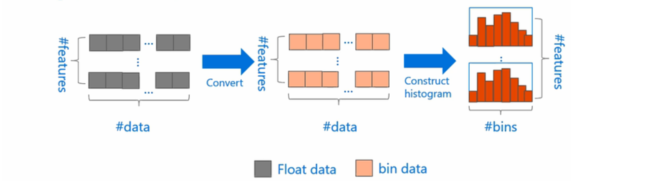
这种离散化分桶思路其实有很多优点的,
- 内存占用更小:xgboost需要用32位的浮点数去存储特征值, 并用32位的整型去存储索引,而Lightgbm的直方图算法不仅不需要额外存储预排序的结果(个人:存储索引),而且只需要保存特征离散化后的值,比如离散为256个bin时,这个值用8位(\(2^8 = 256\))整型存储就足够了,内存消耗可以降低为原来的1/8,节省7/8。
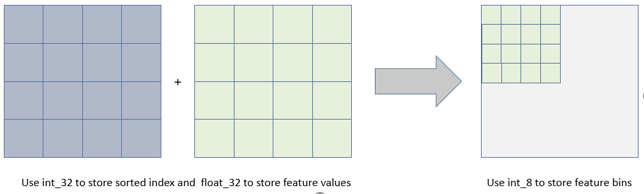
- 计算代价更小:减小了split finding时计算增益的计算量,相比于XGBoost,直接将时间复杂度从 O(#data * #feature) 降低到 O(#bins * #feature) ,而我们知道 #data >> #bins。
Histogram算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在实际的数据集上表明,离散化的分裂点对最终的精度影响并不大,甚至会好一些。原因在于:
- decision tree本身就是一个弱学习器,分割点是不是精确并不是太重要,
- 采用Histogram算法会起到正则化的效果,有效地防止模型的过拟合(bin数量决定了正则化的程度,bin越少惩罚越严重,欠拟合风险越高)。
直方图算法可以起到的作用就是可以减小分割点的数量, 加快计算。
直方图作差加速
除此之外,LightGBM 在节点分裂时还采用了直方图做差加速。对于此节点选中的分裂特征,它的子节点的直方图在分裂点一刀切开就好了,但对于没被选中的特征的子节点的直方图,还要按照此节点选中特征所确定的分裂规则,重新构建左、右节点的子直方图。
这里可以用直方图做差加速的方法,加速这一过程。在构建叶节点的直方图时,当父节点分裂时,它的直方图是已知的,只要求出一个叶子节点的直方图,另一个叶子节点的就可以做差得到,减少了算量。我们还可以通过父节点的直方图与相邻叶节点的直方图相减的方式构建,从而减少了一半的计算量,提升一倍速度。(个人:也就是省去了上面直方图算法的前三步,直接得到第四步的结果)。在实际操作过程中,我们还可以先计算直方图小的叶子节点,然后利用直方图作差来获得直方图大的叶子节点。

稀疏特征优化
这里注意一下,XGBoost 在进行预排序时只考虑非零值进行加速,而 LightGBM 也采用类似策略:只用非零特征构建直方图。
LightGBM独有的两大先进技术(GOSS & EFB)
到了这里,才是Lightgbm的亮点所在, 下面的这两大技术是Lightgbm相对于xgboost独有的, 分别是单边梯度抽样算法(GOSS)和互斥特征捆绑算法(EFB)。
- GOSS可以减少样本的数量,
- 而EFB可以减少特征的数量,
这样就能降低节点分裂过程中的复杂度。
单边梯度抽样算法(GOSS)
单边梯度抽样算法(Gradient-based One-Side Sampling,GOSS),
- 是从减少样本的角度出发,
- 排除大部分权重小的样本,
- 仅用剩下的样本计算信息增益,
- 它是一种在减少数据和保证精度上平衡的算法。
我们知道,
- 在AdaBoost中,会给每个样本一个权重,然后每一轮之后调大错误样本的权重,让后面的模型更加关注前面错误区分的样本,这时候样本权重是数据重要性的标志。
- 到了GBDT中, 确实没有一个像Adaboost里面这样的样本权重,既然Lightgbm是GBDT的变种,应该也没有原始样本的权重,理论上说是不能应用权重进行采样的,但是GBDT中每个数据都会有不同的梯度值, 这个对采样是十分有用的, 即梯度小的样本,训练误差也比较小,说明数据已经被模型学习的很好了,因为GBDT不是聚焦残差吗? 在训练新模型的过程中,梯度比较小的样本对于降低残差的作用效果不是太大,所以我们可以关注梯度高的样本,这样就减少计算量。
但是盲目的直接去掉这些梯度小的数据,这样就会改变数据的分布,
- GOSS 算法保留了梯度大(梯度绝对值大)的样本,
- 并对梯度小的样本随机抽样一个子集,
- 为了不改变样本的数据分布,在计算增益时为梯度小的样本引入一个常数进行平衡,让这个子集可以近似到误差小的数据的全集。这个系数是:
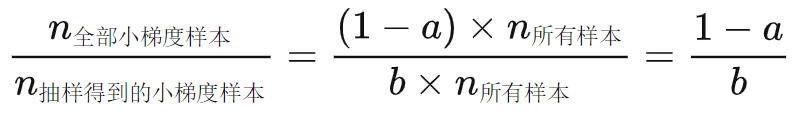
解释下算法名字 ——基于梯度的单边采样:
- 基于梯度体现在按照梯度顺序排序;
- 单边采样体现在只在小梯度样本这边采样。

我们可以看到
- GOSS算法事先基于梯度的绝对值对样本进行排序(无需保存排序后结果),假设样本个数为#samples,然后拿到前a比例的大梯度的样本(拿到的大梯度样本个数为a * #samples),和在剩下的样本中随机抽取一个个数为b * # samples的小梯度样本子集,
- 在计算增益时,通过乘上 \(\frac{1-a}{b}\) 来放大梯度小的样本的权重。
- 一方面,算法将更多的注意力放在训练不足的样本上,另一方面,通过乘上权重来防止采样对原始数据分布造成太大的影响。
Lightgbm正是通过单边梯度抽样算法这样的方式,在几乎不影响精度的情况下,减少了样本数量,使得训练速度加快。
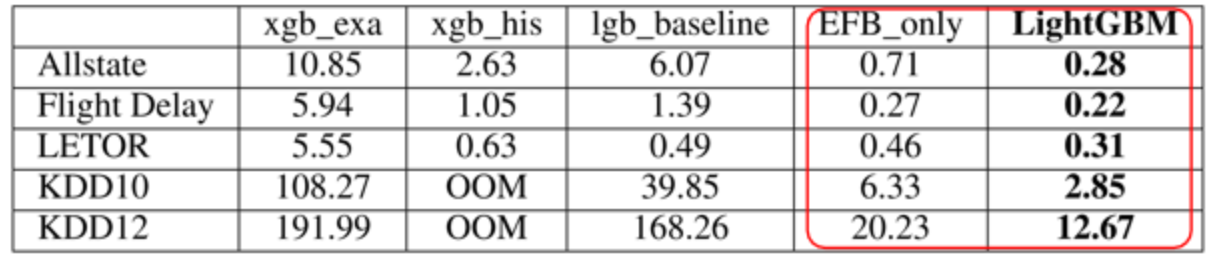
作者在五个数据集上进行了测试,如下表,表中数值为训练单棵决策树需要的秒数。这里只需要关注红框中的两列,其中 EFB_only 这列是只使用了 EFB(互斥特征捆绑)的 LightGBM 方法,另一列是完整的 LightGBM 算法。所以这两列差别在于左边的没用 GOSS,右边的用了,因此可以用于对比 GOSS 效果。很明显,GOSS 平均能提速一倍左右。
互斥特征捆绑算法(EFB)
特征多,可降维。LightGBM 利用稀疏性,对特征进行无损合并。
- 从特征角度来看,稀疏特征会包含很多 0 元素;
- 从样本角度来看,一个样本的多个稀疏特征经常同时为 0。
EFB 基于这种想法,对互斥特征进行了捆绑,整体过程有点类似于 One-Hot 逆过程,以下图为例详细介绍。
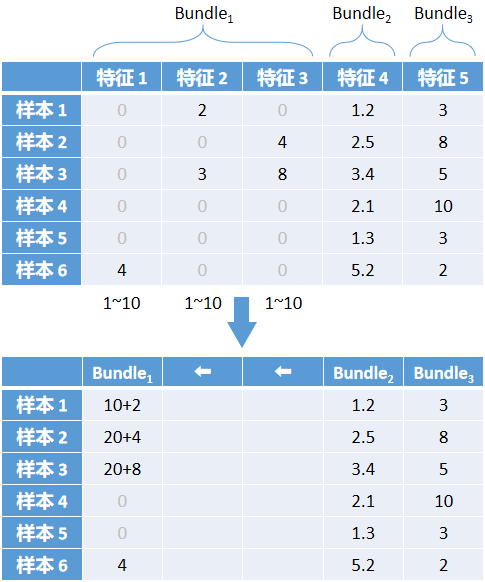
先看第一个表格,这个是没做 EFB 的原表格。表格里有 6 个样本,每个样本有 5 个特征,前 3 个特征稀疏,后 2 个特征稠密。稠密特征不管,只看稀疏特征,目标是把这三个稀疏特征合并成一个新特征,并把这个新特征叫做 Bundle。 当一行样本的 3 个稀疏特征中只有 1 个非零元素时,可以忽略 0 元素,只保留非零元素,这样就实现了 3 -> 1 的降维。
但是显然这样没办法实现 1 -> 3 的还原,因为不清楚合并后得到的非零元素是哪个原始特征的,这就说明我们在合并时损失了一些信息。
可以通过数据分布范围内涵地表示合并后元素所属哪个原特征。假设三个特征分布范围都为 1~10,第一个特征不动,第二个特征错开第一个分布,全体元素在坐标轴上向右偏移 10,第三个特征错开前两个特征,全体元素向右偏移20。这样就形成了箭头下方的第二个表格,每个元素可以根据大小范围判断属于哪个原特征。
你肯定注意到了样本 3 在合并的时候,有两个非零元素,不符合要求。LightGBM 把这种情况定义为冲突。如果完全拒绝这种情况,那其实可以合并的特征会很少,所以没办法只能适当容忍冲突。 当几个特征冲突比例小(源码给的阈值是 \(\frac {1} {10000}\) )的时候,影响不大,忽略冲突,把这几个特征叫做互斥特征;当冲突比例大的时候,不能忽略,EFB 不适用。那么对于样本 3 这种冲突情况,以最后参与合并的特征为准,所以表格里是 20+8 而不是 10+3。
高维度的数据往往是稀疏的,这种稀疏性启发我们设计一种无损的方法来减少特征的维度。
- 通常被捆绑的特征都是互斥的(即特征不会同时为非零值,像one-hot),这样两个特征捆绑起来才不会丢失信息。
- 如果两个特征并不是完全互斥(部分情况下两个特征都是非零值),可以用一个指标对特征不互斥程度进行衡量,称之为冲突比例,当这个值较小时,我们可以选择把不完全互斥的两个特征捆绑,而不影响最后的精度。
所以,互斥特征捆绑算法(Exclusive Feature Bundling)是从减少特征的角度去帮助Lightgbm更快, 它指出,如果将一些特征进行融合绑定,则可以降低特征数量。这样在构建直方图的时候时间复杂度从O ( # d a t a × # f e a t u r e ) 变成O ( # d a t a × #bundle),这里的#bundle指的特征融合后特征包的个数,且#bundle<<#feature。这样又可以使得速度加快了.
针对这种想法,我们会遇到两个问题:
- 哪些特征可以一起绑定?
- 特征绑定后,特征值如何确定?
对于问题一:
EFB 算法利用特征和特征间的关系构造一个加权无向图,并将其转换为图着色算法。我们知道图着色是个 NP-Hard 问题,故采用贪婪算法得到近似解,具体步骤如下:
- 首先将所有的特征看成图的各个顶点,将不相互独立的特征用一条边连起来,边的权重就是两个相连接的特征的冲突程度:总冲突值(也就是这两个特征上同时不为0的样本个数)。
- 然后按照节点的度对特征降序排序, 度越大,说明与其他特征的冲突越大
- 对于每一个特征, 遍历已有的特征簇,如果发现该特征加入到特征簇中的冲突数不超过某一个阈值,则将该特征加入到该簇中。 如果该特征不能加入任何一个已有的特征簇,则新建一个簇,将该特征加入到新建的簇中,使得总体冲突最小。
算法允许两两特征并不完全互斥来增加特征捆绑的数量,通过设置最大冲突比例\(\gamma\)来平衡算法的精度和效率。
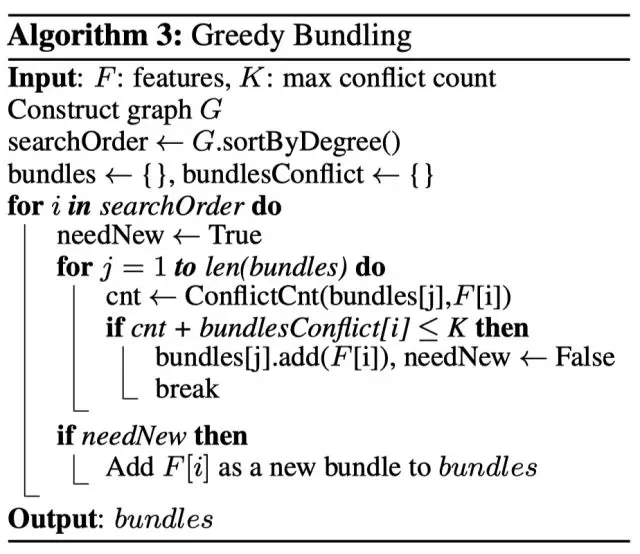
上面这个过程的时间复杂度其实是O(#feature^2)的,因为要遍历特征,每个特征还要遍历所有的簇, 在特征不多的情况下可以应付,但如果特征维度达到百万级别,计算量则会非常大。为了改善效率,我们提出了一个更快的解决方案:统计特征非零值的个数,按非零值个数的降序顺序遍历,因为非零值越多,冲突的概率会越大。
对于问题二:
捆绑完了之后特征应该如何取值呢?这里面的一个关键就是原始特征能从合并的特征中分离出来, 这是什么意思? 绑定几个特征在同一个bundle里需要保证绑定前的原始特征的值可以在bundle里面进行识别,考虑到直方图算法将连续的值保存为离散的bins,我们可以使得簇中不同特征的值所对应的bins不重叠,这可以通过在特征值中加入一个偏置常量来解决。
比如,我们把特征A和B绑定到了同一个bundle里面, A特征的原始取值区间[0,10), B特征原始取值区间[0,20), 这样如果直接绑定,那么会发现我从bundle里面取出一个值5, 就分不出这个5到底是来自特征A还是特征B了。 所以我们可以在B特征的取值上加一个常量10转换为[10, 30),这样绑定好的特征取值就是[0,30), 我如果再从bundle里面取出5, 就一下子知道这个是来自特征A的。 这样就可以放心的融合特征A和特征B了。

作者在五个数据集上进行了测试,如下表,表中数值为训练单棵决策树需要的秒数,这里只需要关注红框中的两列,其中 lgb_baseline 这列是使用了普通稀疏优化的 LightGBM 方法,EFB_only 是使用了 EFB 的 LightGBM 方法,EFB 让速度提升了 8 倍左右。
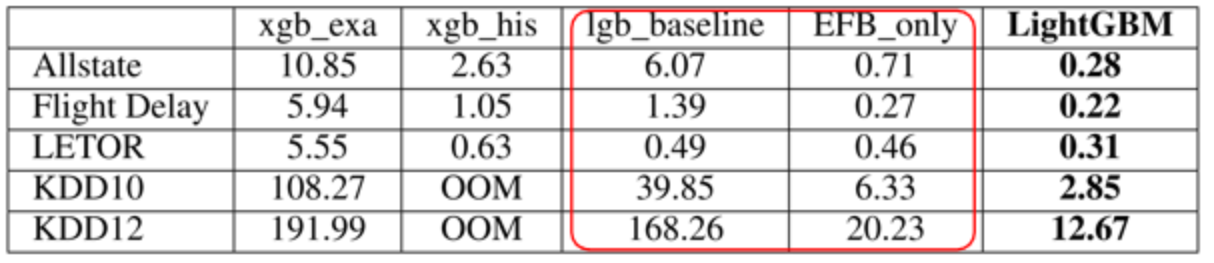
速度提升主要来源于两点:
- 普通的稀疏优化要保存非零值表,用了互斥特征捆绑后,多个稀疏特征捆绑成稠密特征,不用非零值表,节省了内存和维护耗时;
- 在多个稀疏特征间依次遍历时,每次特征切换都存在缓存命中率低(cache miss)的问题,合为一个特征后,不用切换特征,也就没有缓存命中率低的问题了。
带深度限制的Leaf-wise生长策略
在建树的过程中有两种策略:
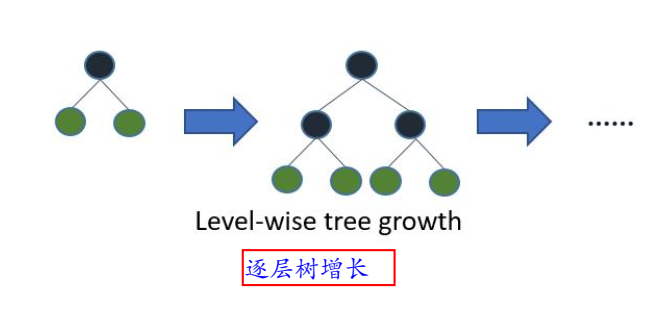
- Level-wise:基于层进行生长,直到达到停止条件;
- Leaf-wise:每次分裂增益最大的叶子节点,直到达到停止条件。
那么lightgbm在树的生成过程中也进行了优化, 它抛弃了xgboost里面的按层生长(level-wise), 而是使用了带有深度限制的按叶子生长(leaf-wise)。
我们知道XGBoost 在树的生成过程中采用 Level-wise 的增长策略,
- 该策略遍历一次数据可以同时分裂同一层的叶子,容易进行多线程优化,
- 也好控制模型复杂度,不容易过拟合。
- 但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,实际上很多叶子的分裂增益较低,没必要进行搜索和分裂,增加了计算量。
而LightGBM采用的Leaf-wise 增长策略则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise 相比,在分裂次数相同的情况下,Leaf-wise 可以降低更多的误差,得到更好的精度。

Leaf-wise 的缺点是
- 可能会长出比较深的决策树,产生过拟合。因此 LightGBM 在 Leaf-wise 之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
- 同时由于每次都需要计算增益最大的节点,所以无法并行分裂。
尽管如此,哪有那么十全十美的东西, 并且作者也使用了max_depth来控制树的高度。 其实敢用Leaf-wise还有一个原因就是Lightgbm在做数据合并,直方图和GOSS等各个操作的时候,其实都有天然正则化的作用,所以作者感觉在这里使用Leaf-wise追求高精度是一个不错的选择。
支持类别特征(寻找类别特征最优分裂点)
LightGBM是第一个直接支持类别特征的GBDT工具。大部分的机器学习算法都不能直接支持类别特征,一般都会对类别特征进行编码,然后再输入到模型中。常见的处理类别特征的方法为 one-hot 编码,但我们知道,对于决策树来说,其实并不推荐使用独热编码,尤其是特征中类别很多的时候,会存在以下问题:
-
会产生样本切分不平衡问题,切分增益会非常小。如,国籍切分后,会产生是否中国,是否美国等一系列特征,这一系列特征上只有少量样本为 1,大量样本为 0。这种划分的增益非常小:
- 较小的那个拆分样本集,它占总样本的比例太小。最后计算得到的增益中来自这个节点的无论增益多大,乘以该比例之后几乎可以忽略;
- 较大的那个拆分样本集,它几乎就是原始的样本集,对最后计算得到的增益的贡献几乎为零;
-
影响决策树学习:决策树依赖的是数据的统计信息,而独热码编码会把数据切分到零散的小空间上。在这些零散的小空间上统计信息不准确的(这些小空间上的数据量小,统计出来的信息可能不准确),学习效果变差。本质是因为独热编码之后的特征的表达能力较差的,特征的预测能力被人为的拆分成多份,每一份与其他特征竞争最优划分点都失败,最终该特征得到的重要性会比实际值低。
对于类别特征,一般是 One-Hot 编码,然后输入到决策树里。这样决策树在学习节点分裂时,是一种 one-vs-rest 模式,每次只能根据一个类别做分类,如下图。这种模式效率比较低,而且不利于决策树学习。LightGBM 对此进行了优化,采用 many-vs-many 模式分裂节点,如下图。
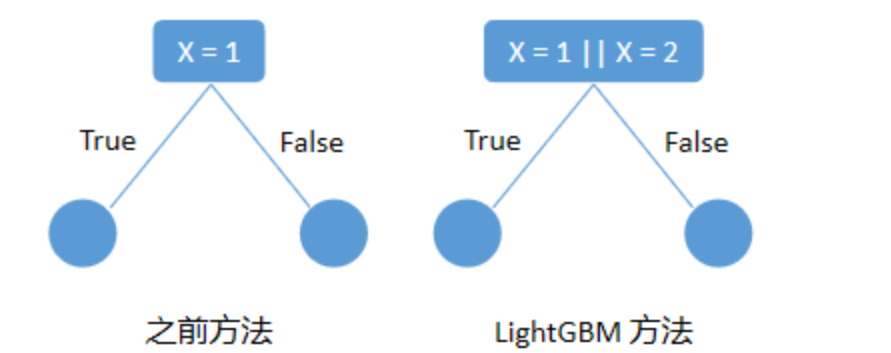
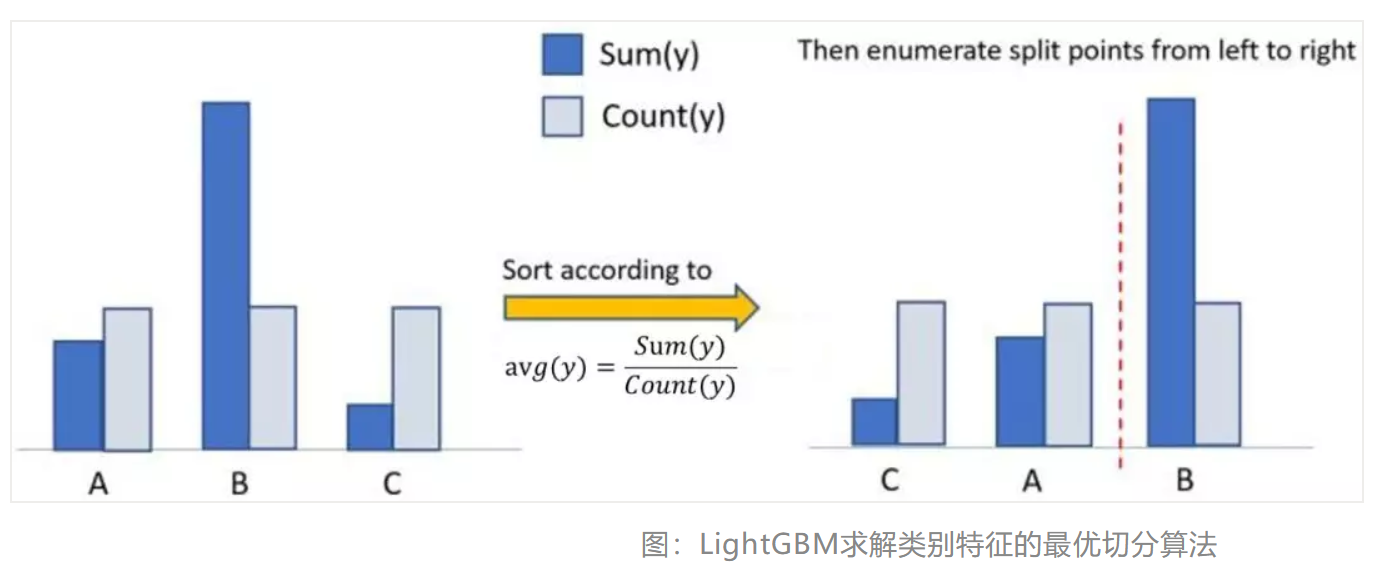
LightGBM 原生支持类别特征,采用many-vs-many的切分方式将类别特征分为两个子集,实现类别特征的最优切分。假设有某维特征有\(k\)个类别,则有\(2^{(k-1)} - 1\)中可能(划分为左右两个子集的所有情况有\(2^k - 2\),由于不能将所有的类别全部划到一个子集中,另一个子集中什么也没有,所有这个式子需要减去2.而我们的划分是不需要区分左右的,所以还需要除以2,最后得到\(2^{(k-1)} - 1\)),时间复杂度为\(O(2^k)\),LightGBM基于Fisher大佬的《On Grouping For Maximum Homogeneity》实现了\(O(klog_2k)\)的时间复杂度。LightGBM 基于这篇文章《On Grouping for Maximum Homogeneity》,对类别特征按照每类的 \(\frac {G} {H} = \frac{∑gradient} {∑hessian}\) 进行排序,然后按照这个顺序构造直方图,寻找最优分裂点。
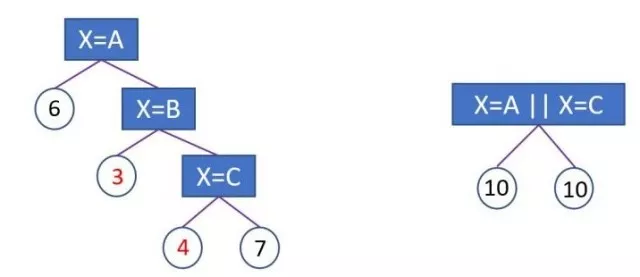
上图左边为基于 one-hot 编码进行分裂,后图为 LightGBM 基于 many-vs-many 进行分裂,右边叶子节点的含义是X = A或者X = C 放到左孩子,其余放到右孩子, 右边的切分方法,数据会被切分到两个比较大的空间,进一步的学习也会更好。
这里有一个机器学习常识问题:为什么连续特征可以直接构建直方图,但类别特征要按照\(\frac {G} {H}\)的顺序构建直方图,而不能按照特征值顺序构建?因为连续特征中的数值具有大小关系,但类别特征中数值没有大小关系,只是代表某类,比如橘子和苹果这两类,它们不分伯仲。而基于直方图的节点分裂,要求特征中数值具有大小关系,所以类别特征要按\(\frac {G} {H}\) 排个序,引入大小关系,之后再构建直方图。
算法流程如下图所示,
- 在枚举分割点之前,先把直方图按照每个类别对应的label均值进行排序;
- 然后按照排序的结果依次枚举最优分割点.
从下图可以看到,\(\frac {Sum(y)}{Count(y)}\)为类别的均值.当然,这个方法很容易过拟合,所以LightGBM里面还增加了很多对于这个方法的约束和正则化。
工程优化
并行优化(Optimization in parallel learning)
我们知道,并行计算可以使得速度更快,lightgbm 支持三个角度的并行:
- 特征并行
- 数据并行
- 投票并行

这些算法适用于不同场景,如下表所示:

下面我们一一来介绍。
特征并行
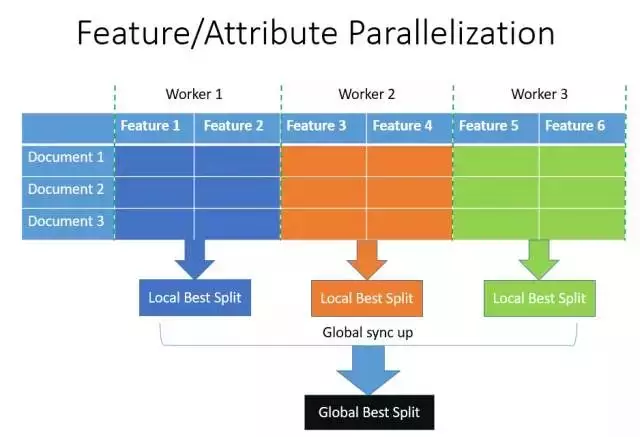
我们先来看一下XGBoost上所使用的传统的特征并行:
- 垂直切分数据, 每个worker只有部分特征
- 每个worker找到局部最佳切分点( feature, threshold)
- worker之间互相通信, 找到全局最佳切分点
- 具有全局最佳切分特征的worker进行节点分裂, 然后广播
切分后左右子树的instance indices - 其他worker根据广播的instance indices进行节点分裂
sync up:同步,
这种特征并行方法有个很大的缺点:需要告知每台机器最终划分结果,增加了额外的复杂度(因为对数据进行垂直划分,每台机器所含数据不同,划分结果需要通过通信告知,网络通信代价大)。
LightGBM 则不进行数据垂直划分,而是
- 每个worker保存所有数据集
- 每个worker在其特征子集上寻找最佳切分点
- worker之间互相通信, 找到全局最佳切分点
- 每个worker根据全局最佳切分点在本地进行节点分裂
这种方式避免广播instance indices, 减小网络通信量。缺点是当数据量比较大时, 单个worker存储所有数据代价高。
数据并行
传统的数据并行
- 水平切分数据, 每个worker只有部分数据
- 每个worker根据本地数据统计局部直方图
- 合并所有局部直方图得到全局直方图
- 根据全局直方图进行节点分裂
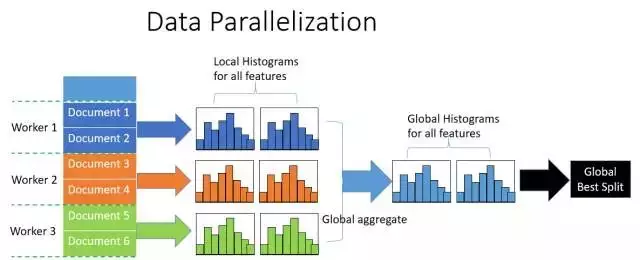
这种方式的缺点是网络通信代价巨大,
- 采用点对点通信算法(point-to-point communication algorithm),每个worker通信量为 O(#machine * #feature * #bin),
- 采用All Reduce并行算子集成的通信算法(collective communication algorithm),每个worker通信量为O(2 * #feature * #bin)。
LightGBM的数据并行算法
- LightGBM算法使用分散规约(Reduce Scatter)并行算子归并来自不同worker的不同特征子集的直方图,然后在局部归并的直方图中找到最优局部分裂信息,最终同步找到最优的分裂信息.(使用分散规约 (Reduce scatter)并行算子 把直方图合并的任务分摊到不同的机器,降低通信和计算)
- 除此之外,LightGBM使用直方图减法加快训练速度。我们只需要对其中一个子节点进行数据传输,另一个子节点可以通过histogram subtraction得到。
- LightGBM可以将传输代价降低为O(0.5 * #feature * #bin)。
投票并行
针对数据量特别大特征也特别多的情况下,可以采用投票并行。投票并行主要针对数据并行时,数据合并的通信代价比较大的瓶颈进行优化,当特征数量很大时,数据并行会有巨大的通信代价,但是如果能够降低需要通信的特征数量,数据并行将是一个非常好的方法。选举并行就是基于这种想法设计的,其通过投票的方式只合并部分特征的直方图从而达到降低通信量的目的。
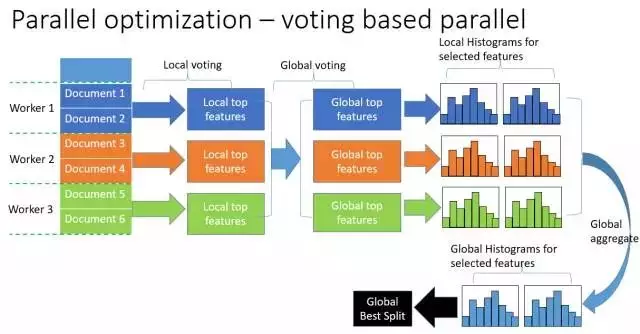
具体方法如下:
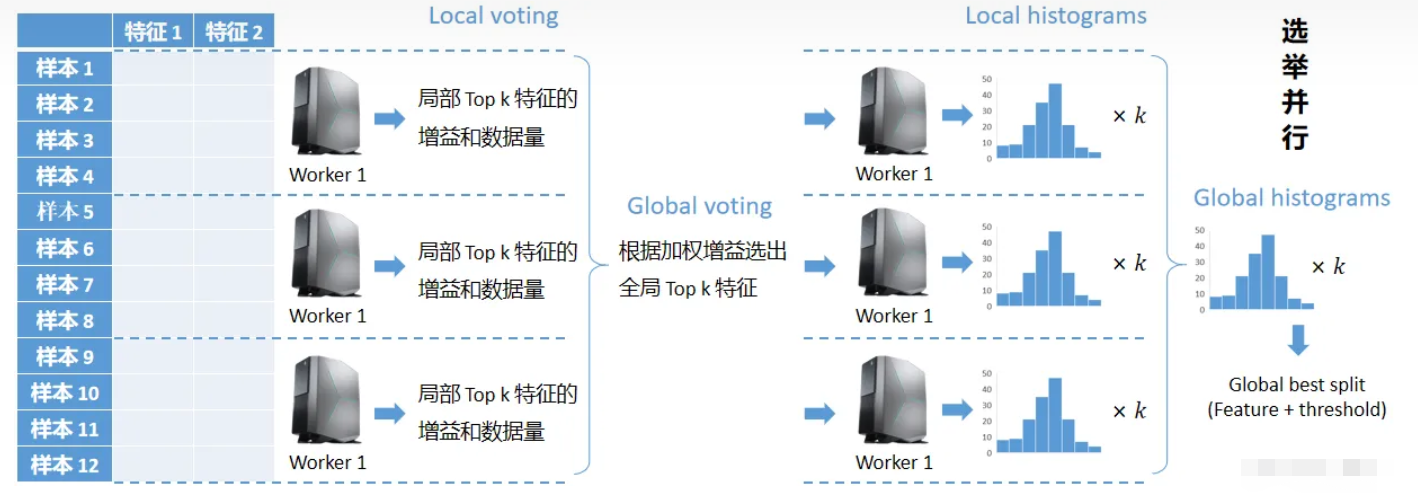
- 让每个worker根据增益选出k个最有潜力竞争全局最优的特征,叫做局部最优特征,
- 把这些局部最优特征所对应的增益和用来计算增益的数据量\(n_{sample}\)进行汇总,
- 考虑到样本少的增益不可靠,所以把\(\frac {n_{sample}} {\max(all \text{ } n_{sample})}\) 作为权重,对增益进行加权,
- 不同worker可能选出了相同的局部最优特征,这种情况直接把它们的加权增益加一起就好,
- 根据加权增益排序,再一次选出k个最有潜力竞争全局最优的特征,叫做全局最优特征,
- 各个worker只发送k个全局最优特征的局部直方图,汇总后找出最优分裂点,
有理论证明,这种voting parallel以很大的概率选出实际最优的特征。
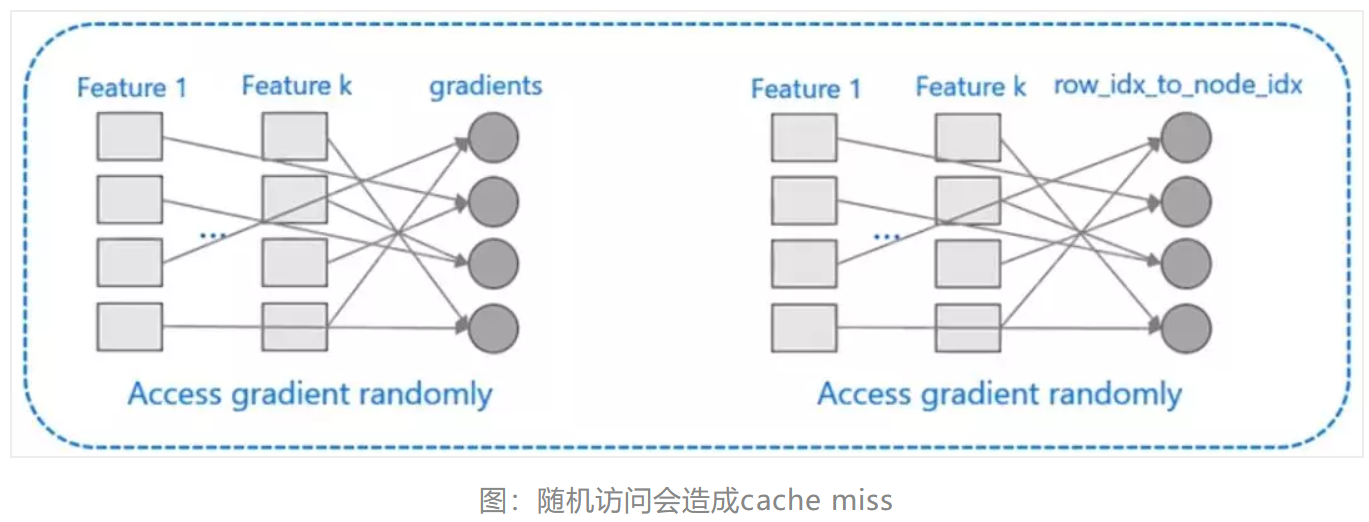
Cache命中率优化
XGBoost对cache优化不友好,如下图所示。在预排序后,特征对梯度的访问是一种随机访问,并且不同的特征访问的顺序不一样,无法对cache进行优化。同时,在每一层长树的时候,需要随机访问一个行索引到叶子索引的数组,并且不同特征访问的顺序也不一样,也会造成较大的cache miss。为了解决缓存命中率低的问题,XGBoost 提出了缓存访问算法进行改进。
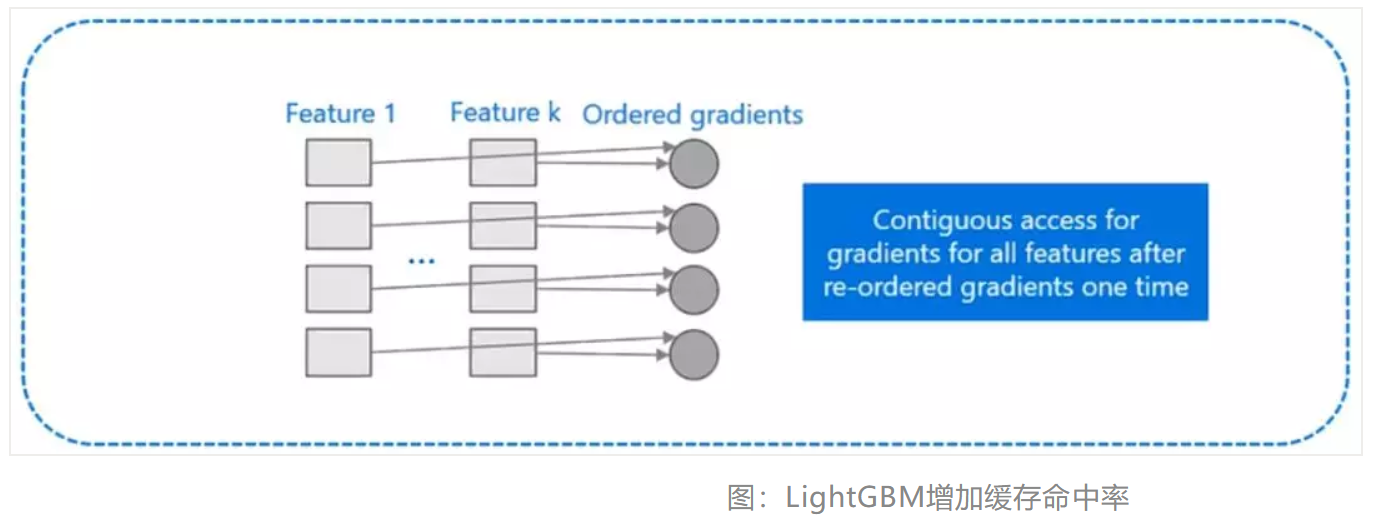
而 LightGBM 所使用直方图算法对 Cache 天生友好:
- 首先,所有的特征都采用相同的方式获得梯度(区别于XGBoost的不同特征通过不同的索引获得梯度),只需要对梯度进行排序并可实现连续访问,大大提高了缓存命中率;
- 其次,因为不需要存储行索引到叶子索引的数组,降低了存储消耗,而且也不存在 Cache Miss的问题。
小结
下面总结一下LightGBM相对于XGBoost的优点,从内存和速度两方面进行介绍。
内存更小:
- XGBoost 使用预排序后需要记录样本特征值及其对应样本的梯度信息统计值的索引,而 LightGBM 使用了直方图算法将特征值转变为bin值,且不需要记录特征到样本的索引,将空间复杂度从 O(2*#data) 降低为 O(#bin),极大的减少了内存消耗;
- LightGBM 采用了直方图算法将存储特征值转变为存储 bin 值,降低了内存消耗;
- LightGBM 在训练过程中采用互斥特征捆绑算法减少了特征数量,降低了内存消耗。
速度更快:
- LightGBM 采用了直方图算法将遍历样本转变为遍历直方图,极大的降低了时间复杂度;
- LightGBM 在训练过程中采用单边梯度算法过滤掉梯度小的样本,减少了大量的计算;
- LightGBM 采用了基于 Leaf-wise 算法的增长策略构建树,减少了很多不必要的计算量;
- LightGBM 采用优化后的特征并行、数据并行方法加速计算,当数据量非常大的时候还可以采用投票并行的策略;
- LightGBM 对缓存也进行了优化,增加了 Cache hit 的命中率;
LightGBM工具库的使用
实例
LightGBM有两大类接口:LightGBM原生接口 和 scikit-learn接口,下面我们分别使用这两种接口进行分类和回归任务进行举例。
基于LightGBM原生接口的分类和回归:
- 分类:
import lightgbm as lgb
from sklearn import datasets
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.metrics import roc_auc_score, accuracy_score
# 加载数据
iris = datasets.load_iris()
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)
# 转换为Dataset数据格式
train_data = lgb.Dataset(X_train, label=y_train)
validation_data = lgb.Dataset(X_test, label=y_test)
# 参数
params = {
'learning_rate': 0.1,
'lambda_l1': 0.1,
'lambda_l2': 0.2,
'max_depth': 4,
'objective': 'multiclass', # 目标函数
'num_class': 3,
}
# 模型训练
gbm = lgb.train(params, train_data, valid_sets=[validation_data])
# 模型预测
y_pred = gbm.predict(X_test)
y_pred = [list(x).index(max(x)) for x in y_pred]
print(y_pred)
# 模型评估
print(accuracy_score(y_test, y_pred))
- 回归:
对于LightGBM解决回归问题,我们用Kaggle比赛中回归问题:House Prices: Advanced Regression Techniques,地址:https://www.kaggle.com/c/house-prices-advanced-regression-techniques 来进行实例讲解。
该房价预测的训练数据集中一共有81列,第一列是Id,最后一列是label,中间79列是特征。这79列特征中,有43列是分类型变量,33列是整数变量,3列是浮点型变量。训练数据集中存在缺失值。
import pandas as pd
from sklearn.model_selection import train_test_split
import lightgbm as lgb
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import Imputer
# 1.读文件
data = pd.read_csv('./dataset/train.csv')
# 2.切分数据输入:特征 输出:预测目标变量
y = data.SalePrice
X = data.drop(['SalePrice'], axis=1).select_dtypes(exclude=['object'])
# 3.切分训练集、测试集,切分比例7.5 : 2.5
train_X, test_X, train_y, test_y = train_test_split(X.values, y.values, test_size=0.25)
# 4.空值处理,默认方法:使用特征列的平均值进行填充
my_imputer = Imputer()
train_X = my_imputer.fit_transform(train_X)
test_X = my_imputer.transform(test_X)
# 5.转换为Dataset数据格式
lgb_train = lgb.Dataset(train_X, train_y)
lgb_eval = lgb.Dataset(test_X, test_y, reference=lgb_train)
# 6.参数
params = {
'task': 'train',
'boosting_type': 'gbdt', # 设置提升类型
'objective': 'regression', # 目标函数
'metric': {'l2', 'auc'}, # 评估函数
'num_leaves': 31, # 叶子节点数
'learning_rate': 0.05, # 学习速率
'feature_fraction': 0.9, # 建树的特征选择比例
'bagging_fraction': 0.8, # 建树的样本采样比例
'bagging_freq': 5, # k 意味着每 k 次迭代执行bagging
'verbose': 1 # <0 显示致命的, =0 显示错误 (警告), >0 显示信息
}
# 7.调用LightGBM模型,使用训练集数据进行训练(拟合)
# Add verbosity=2 to print messages while running boosting
my_model = lgb.train(params, lgb_train, num_boost_round=20, valid_sets=lgb_eval, early_stopping_rounds=5)
# 8.使用模型对测试集数据进行预测
predictions = my_model.predict(test_X, num_iteration=my_model.best_iteration)
# 9.对模型的预测结果进行评判(平均绝对误差)
print("Mean Absolute Error : " + str(mean_absolute_error(predictions, test_y)))
基于Scikit-learn接口的分类和回归:
- 分类:
from lightgbm import LGBMClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.externals import joblib
# 加载数据
iris = load_iris()
data = iris.data
target = iris.target
# 划分训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2)
# 模型训练
gbm = LGBMClassifier(num_leaves=31, learning_rate=0.05, n_estimators=20)
gbm.fit(X_train, y_train, eval_set=[(X_test, y_test)], early_stopping_rounds=5)
# 模型存储
joblib.dump(gbm, 'loan_model.pkl')
# 模型加载
gbm = joblib.load('loan_model.pkl')
# 模型预测
y_pred = gbm.predict(X_test, num_iteration=gbm.best_iteration_)
# 模型评估
print('The accuracy of prediction is:', accuracy_score(y_test, y_pred))
# 特征重要度
print('Feature importances:', list(gbm.feature_importances_))
# 网格搜索,参数优化
estimator = LGBMClassifier(num_leaves=31)
param_grid = {
'learning_rate': [0.01, 0.1, 1],
'n_estimators': [20, 40]
}
gbm = GridSearchCV(estimator, param_grid)
gbm.fit(X_train, y_train)
print('Best parameters found by grid search are:', gbm.best_params_)
- 回归:
import pandas as pd
from sklearn.model_selection import train_test_split
import lightgbm as lgb
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import Imputer
# 1.读文件
data = pd.read_csv('./dataset/train.csv')
# 2.切分数据输入:特征 输出:预测目标变量
y = data.SalePrice
X = data.drop(['SalePrice'], axis=1).select_dtypes(exclude=['object'])
# 3.切分训练集、测试集,切分比例7.5 : 2.5
train_X, test_X, train_y, test_y = train_test_split(X.values, y.values, test_size=0.25)
# 4.空值处理,默认方法:使用特征列的平均值进行填充
my_imputer = Imputer()
train_X = my_imputer.fit_transform(train_X)
test_X = my_imputer.transform(test_X)
# 5.调用LightGBM模型,使用训练集数据进行训练(拟合)
# Add verbosity=2 to print messages while running boosting
my_model = lgb.LGBMRegressor(objective='regression', num_leaves=31, learning_rate=0.05, n_estimators=20,
verbosity=2)
my_model.fit(train_X, train_y, verbose=False)
# 6.使用模型对测试集数据进行预测
predictions = my_model.predict(test_X)
# 7.对模型的预测结果进行评判(平均绝对误差)
print("Mean Absolute Error : " + str(mean_absolute_error(predictions, test_y)))
自定义objective function和eval metric
这个来自官网的例子,https://github.com/microsoft/LightGBM/blob/master/examples/python-guide/advanced_example.py,
# self-defined objective function
# f(preds: array, train_data: Dataset) -> grad: array, hess: array
# log likelihood loss
def loglikelihood(preds, train_data):
labels = train_data.get_label()
preds = 1. / (1. + np.exp(-preds))
grad = preds - labels
hess = preds * (1. - preds)
return grad, hess
# self-defined eval metric
# f(preds: array, train_data: Dataset) -> name: str, eval_result: float, is_higher_better: bool
# binary error
# NOTE: when you do customized loss function, the default prediction value is margin
# This may make built-in evaluation metric calculate wrong results
# For example, we are doing log likelihood loss, the prediction is score before logistic transformation
# Keep this in mind when you use the customization
def binary_error(preds, train_data):
labels = train_data.get_label()
preds = 1. / (1. + np.exp(-preds))
return 'error', np.mean(labels != (preds > 0.5)), False
gbm = lgb.train(params,
lgb_train,
num_boost_round=10,
init_model=gbm,
fobj=loglikelihood,
feval=binary_error,
valid_sets=lgb_eval)
print('Finished 40 - 50 rounds with self-defined objective function and eval metric...')
# another self-defined eval metric
# f(preds: array, train_data: Dataset) -> name: str, eval_result: float, is_higher_better: bool
# accuracy
# NOTE: when you do customized loss function, the default prediction value is margin
# This may make built-in evaluation metric calculate wrong results
# For example, we are doing log likelihood loss, the prediction is score before logistic transformation
# Keep this in mind when you use the customization
def accuracy(preds, train_data):
labels = train_data.get_label()
preds = 1. / (1. + np.exp(-preds))
return 'accuracy', np.mean(labels == (preds > 0.5)), True
gbm = lgb.train(params,
lgb_train,
num_boost_round=10,
init_model=gbm,
fobj=loglikelihood,
feval=[binary_error, accuracy],
valid_sets=lgb_eval)
print('Finished 50 - 60 rounds with self-defined objective function and multiple self-defined eval metrics...')


 浙公网安备 33010602011771号
浙公网安备 33010602011771号