CSP-S-2020-T3
\(\texttt{data-2020-11-13}\)
修正了部分错误,以及增添了一些描述。
考场经历
考场上打了只有加和只有乘的两种特殊情况,然后没时间了,因为 T1 调了太久。
感觉树的形态的部分分是没有用的,都能打树的情况了满分无非就是加个拓扑。(当然也可能有什么我没想到的高妙骗分手段)
Solution
在只有加或乘的情况下,只需要拓扑传递执行次数便可,因为此时满足交换律。
然后就考虑:如何从特殊到一般?在乘和加同时存在的时候,就必须要考虑运算顺序了。
然后就发现其实只有一个地方会有影响:对于每个加法操作 \(i\),后面所有的乘法操作 \(j\) 都会对其产生 \(\times p_j\) 的贡献。
那如果能够做到快速求出每个加法操作被哪些乘法操作所影响(\(\prod p_j\) 即为贡献),我就可以将乘法操作看成是对加法操作执行次数的计算。必然,原数列自然也可以看成一堆加法操作。
思路分析完了,接下来考虑如何实现刚刚嘴巴 AC 的这个东西。
首先这个 \(\prod p_j\) 有两部分,为了讲清楚,我需要画点图。
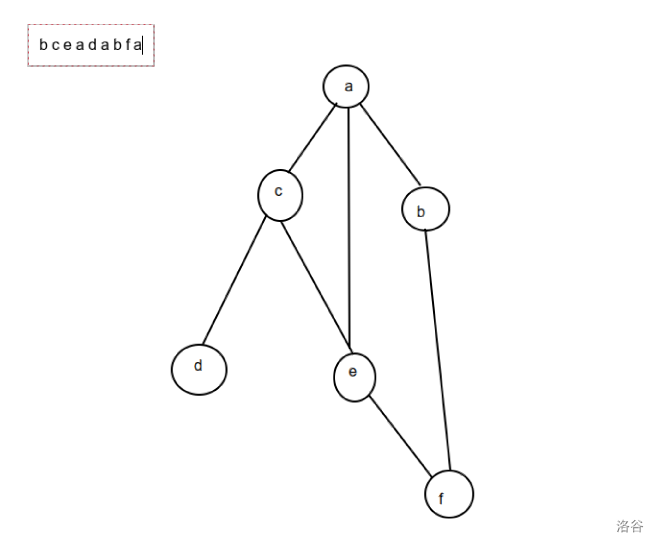
拓扑图中的各点即表示一种操作,边的方向为从上向下(因为画图工具不便所以没有箭头),其中出度为 \(0\) 的点 \(d,f\) 是操作 \(1\) 或 \(2\) ,其余点都是操作 \(3\)。
左上角那个字符串即为大小为 \(m\) 的操作序列。
对于每一个操作 \(3\),设其编号为 \(y\),它都可以拆分成为一个只由操作 \(1\) 和操作 \(2\) 组成的序列 \(q_y\)。拆分完之后,对于 \(q_y\) 中每一个加法,它的贡献分为两部分:
设拆分后的序列长度为 \(k_{...}\)
所有外部的贡献:
以及内部自己贡献:
对于元素 \(q_{y,i}\),有贡献:
这个式子看不懂怎么办?也没有关系,你也可以听我口胡。
你需要计算拆开以后对于每一个加法在自己后面所有乘法的权值积,也就是这个加法的执行次数。
首先这个操作序列很烦,你就可以新建一个操作 \(m+1\),其类型为 \(3\),然后执行顺序就是输入的那一串。
那么此时所有的“序列”指的就是每个操作 \(3\) 的操作执行序列了。
那么假设我们已经能够求出刚刚我说的那个东西,就可以跑一遍拓扑,初始只有操作 \(m+1\) 有一个权值为 \(1\),表示这个操作的实际加法执行次数,然后跑拓扑的时候传递下去。并且每次传递,是要乘上"边权"的。
这个"边权",实际指的是:自己后面所有操作拆分后的所有乘法操作的积。
很容易发现这个东西是可以合并的,因为不会出现递归(自己调用自己),算当前某个点的贡献的时候,它所需调用的东西的信息都已经处理好了,可以倒着跑一遍拓扑来求出的。
信息合并的处理的话,我是维护了一个后缀积 \(s\),其中 \(s_0\) 就是上面所说的这个操作拆分后所有乘法操作的积这一项,然后因为顺序和可重这两个因素,所以并不是向上传递,而是向下调用。
后缀积的含义,就是前面那个式子:
然后因为当前在处理的时候,后面那个 \(\prod\) 的值已经处理好了,可以直接写成:
注意点
因为是 vector,调用时可能会越界一位,所以在后缀积末尾赛一个 \(1\) 进去,这样就不用特判了。
如果还没懂可以康康代码,自认为代码还是比较清晰的。
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1e5+3;
const int K=1e6+3;
const int M=998244353;
inline int rin()
{
int s=0;
bool bj=false;
char c=getchar();
for(;(c>'9'||c<'0')&&c!='-';c=getchar());
if(c=='-')bj=true,c=getchar();
for(;c>='0'&&c<='9';c=getchar())s=(s<<1)+(s<<3)+(c^'0');
if(bj)s=-s;
return s;
}
struct milk
{
LL ads;//实际加法执行次数
int typ;
int p,v;//如题意
int d_1,d_2;//反/正跑拓扑时用到的度数
vector<int>c;//反着跑拓扑的边
vector<int>C;//正边
vector<int>s;//后缀积
}t[N];
LL a[N];
int b[K];
int d[N];
int n,m,q;
inline void Work_1(int now)
{
if(t[now].typ==2)t[now].s.push_back(t[now].v);
if(t[now].typ==3)
{
int tail=0;
LL j=1;
for(int i=t[now].C.size()-1;i>=0;i--)b[tail++]=(j=j*t[t[now].C[i]].s[0]%M);//处理后缀积,这样可以不用写逆元
for(int i=tail-1;i>=0;i--)t[now].s.push_back(b[i]);
}
t[now].s.push_back(1);
}
inline void Tp_1()
{
int i,j;
int head=1,tail=0;
for(i=1;i<=m;i++)if(!t[i].d_1)d[++tail]=i;
for(;head<=tail;)
{
int now=d[head++];
Work_1(now);
for(i=t[now].c.size()-1;i>=0;i--)
{
int to=t[now].c[i];
t[to].d_1--;
if(!t[to].d_1)d[++tail]=to;
}
}
return;
}
inline void Tp_2()
{
int i,j;
int head=1,tail=0;
for(i=1;i<=m;i++)if(!t[i].d_2)d[++tail]=i;
for(;head<=tail;)
{
int now=d[head++];
t[now].ads%=M;
for(i=t[now].C.size()-1;i>=0;i--)
{
int to=t[now].C[i];
t[to].d_2--;
if(!t[to].d_2)d[++tail]=to;
t[to].ads+=t[now].ads*t[now].s[i+1]%M;
}
}
return;
}
int main()
{
int i,j;
for(n=rin(),i=1;i<=n;i++)a[i]=rin();
for(m=rin(),i=1;i<=m;i++)
{
t[i].typ=rin();
t[i].ads=0;
if(t[i].typ<=1)t[i].p=rin();
if(t[i].typ<=2)t[i].v=rin();
if(t[i].typ==3)
{
for(t[i].d_1=j=rin();j>0;j--)
{
int x=rin();
t[i].C.push_back(x);
t[x].c.push_back(i);
t[x].d_2++;
}
}
}
t[++m].typ=3;
t[m].ads=1;
for(t[m].d_1=q=rin();q>0;q--)
{
int x=rin();
t[m].C.push_back(x);
t[x].c.push_back(m);
t[x].d_2++;
}
Tp_1();//第一遍拓扑预处理信息
Tp_2();//第二遍拓扑处理答案
for(i=1;i<=n;i++)a[i]=(a[i]*t[m].s[0]%M);//直接将原数组乘上所有操作拆分开后的乘法积
for(i=1;i<=m;i++)if(t[i].typ==1)a[t[i].p]+=t[i].ads*t[i].v%M;
for(i=1;i<=n;i++)printf("%lld ",a[i]%M);printf("\n");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号