第N个质数（洲阁筛）
\(\texttt{data-2021-01-04}\)
稍微修了一下 Latex 和一些式子，但是不要指望这篇题解写得有多好，毕竟是去年七月的垃圾屑文。
题目：求第 \(\texttt{N}\) 个质数（\(\texttt{N} \le 10^9\))。
普奇神父快乐题
二分答案，然后根据小于等于自己的质数个数来判断自己是否是第 \(\texttt{N}\) 个质数。
此时就把问题转化为了求一定范围内的质数个数。
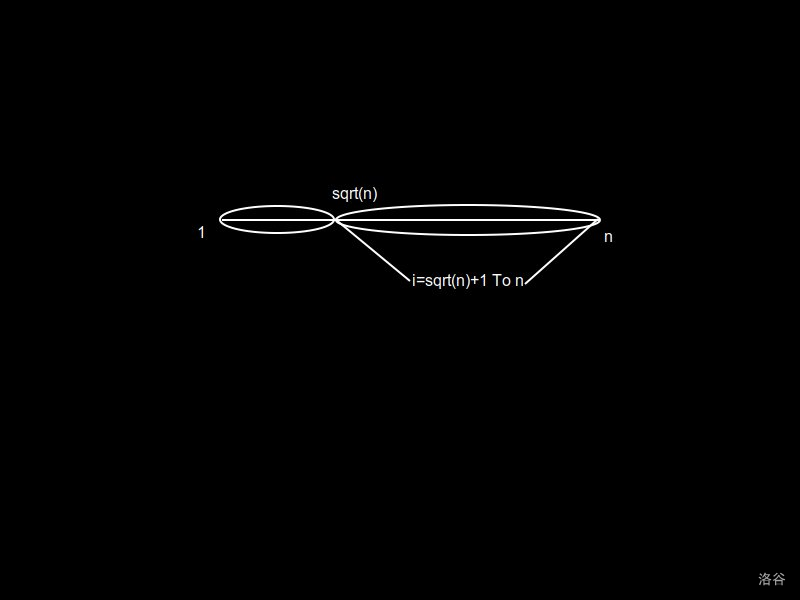
首先我们要知道，\(1-n\) 的数可以分为两段：
-
\([1,\sqrt n]\)
-
\([\sqrt n+1,n]\)
对于大于根号 \(n\) 的数 \(i\)，有两种情况：
-
\(i\) 是质数。
-
\(i\) 不是质数，且必定存在 \(i\) 的约数 \(p\) 满足 \(p\in (1,\sqrt n]\)。
小证（其实非常显然吧）
设：\(\sqrt n +1\le x\le n\) 且 \(x=a\cdot b\)。
如果 \(a,b>\sqrt n\)，会得到 \(x>n\)，不满足假设，因此 \(a,b\) 一定会有一个满足 \(\le \sqrt n\) 的。
至此，证毕。
推导（我觉得是个 DP 的过程）
那么求 \(1\) 到 \(n\) 之间的质数个数 \(f(n)\) 可以拆分为：
我们对于后面那个东西设个函数 \(g(x,y)\) 表示只考虑前 \(y\) 个质数，\(c(y)\) 到 \(x\) 之间有多少数 没有被判断成合数。（可以理解成线性筛中的过程）
注：\(c(y)\) 表示第 \(y\) 个质数。
得：
（关于为什么要 \(-1\) 后面有解释）
然后 \(g(x,y)\) 可以把最后一个质数单独分出来（这里思路很像 Min_25 筛），得到转移式：
其中 \(d(i)\) 表示 \(i\) 的最小质因子。
而后面那个 \(\sum\) 也等于：
函数 \(g\) 的边界判断为：
即只筛了一次，把所有偶数筛掉。
然后还有一条剪枝：
\(\texttt{Q}:\) 为什么：
\(\texttt{A}:\) 因为在 \(g(x/c(y),y-1)\) 这一层 \(c(y)^2\) 也是需要算进去答案的,递归下去之后的计算是应当包括 \(c(y)\) 这个数的。
\(\texttt{Q}:\) 为什么：
\(\texttt{A}:\) 因为实际上我们在 \(g(x,y-1)\) 这一层递归中会把 \(1\) 也当作一个质数，所以最后的答案也是要减 \(1\) 的。第二层递归 \(g(\lfloor\frac{x}{c(y)}\rfloor,y-1)\) 并不会算上 \(1\)，因为至少得是 \(c(y)^2\) 才会使答案加 \(1\)。
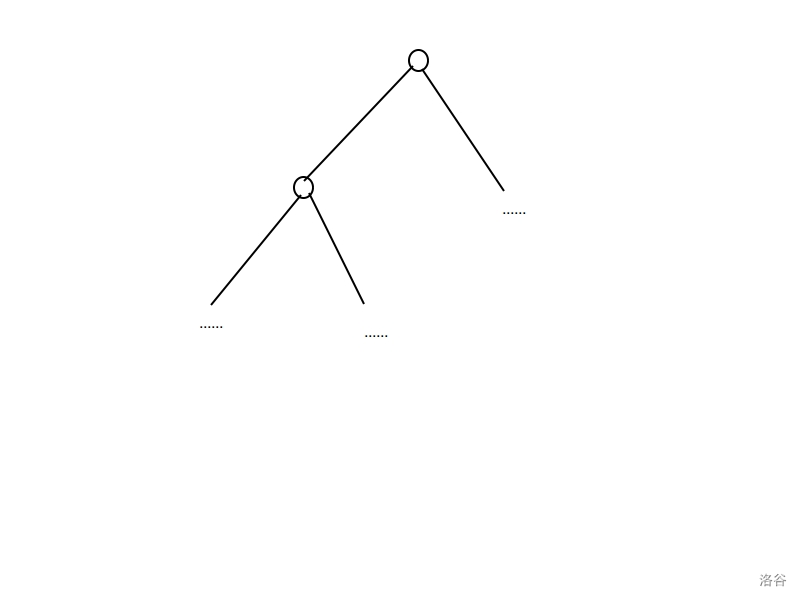
如下图，这个dfs可以建成一颗二叉树，\(g(x,y-1)\) 是左子树，\(g(x/c(y),y-1)\) 是右子树。只有最左边的树边才会算上 \(1\) 这个数并结束然后往上递归，任何一条有向右的边的路径所找到的东西不可能会计算 \(1\) 的贡献。
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const LL MAX=3e10;
const int MAN=1e7+10;
int f[MAN];
int c[MAN];
bool a[MAN];
int n;
inline LL g(LL x,LL y)
{
if(y==1)return (x+1)>>1;//排掉所有偶数
if(x<=MAN-3)
{
LL m=sqrt(x);
if(f[m]<=y)return f[x]+1-y;//可以直接算的范围
}
return g(x,y-1)-g(x/c[y],y-1);
//1--x间被c[y]整除后的商不含（小于c[y]的因数）的个数
}
inline LL cheak(LL mid)
{
LL m=sqrt(mid);
return f[m]+g(mid,f[m])-1;
}
LL rin()
{
LL s=0;
char c=getchar();
bool bj=0;
for(;(c>'9'||c<'0')&&c!='-';c=getchar());
if(c=='-')c=getchar(),bj=true;
for(;c>='0'&&c<='9';c=getchar())s=(s<<1)+(s<<3)+(c^'0');
if(bj)return -s;
return s;
}
int main()
{
LL i,j;
n=rin();
for(i=2;i<=MAN-3;i++)
{
f[i]=f[i-1];
if(!a[i])
{
f[i]++;
c[f[i]]=i;
}
for(j=1;j<=f[i];j++)
{
if(i*c[j]>MAN-3)break;
a[i*c[j]]=true;
if(i%c[j]==0)break;
}
}
LL l=1,r=MAX;
LL ans;
for(;l<=r;)
{
LL mid=(l+r)>>1;
if(cheak(mid)>=n)ans=mid,r=mid-1;
else l=mid+1;
}
printf("%lld",ans);
return 0;
}
