桥头巨炮轰基地？题解

蒟蒻出的签到题。。。

一句话题面：

给定 \(n\) , \(m\) ，\(t\) ， \(p\) （数据保证 \(p\) 是质数）。随机生成长度为 \(n\) 的序列，每个数都是整数且取值为 \([\ 1,m\ ]\) 。

\(t\) 次询问，每次求这个序列单调不增，并且最后一位恰好是 \(k\) 的概率。

题解

首先有一个 \(O(n^2)\) 的来自 \(cyh\) 的暴力 \(DP\)。
大体就是设 \(f_{i,j}\) 表示长度为 \(i\) ，并且结尾的数大于等于 \(j\) 的方案数，
然后暴力转移即可。

For(i,1,m) f[1][i] = m-i+1;
For(i,2,n) rFor(j,m,1) f[i][j] = (f[i][j+1] + f[i-1][j]) %mod;
long long tans=0;
while( q-- ) {
	int x=readd()%m+1;
	tans+=(f[n][x]-f[n][x+1]+mod)*down%mod;
}

通过 打表 观察DP式子，可以发现方案数是和组合数有关的，并且大体是呈斜线的杨辉三角。
推出来式子是：

\[\binom{n+m-k-1}{n-1} \]

考虑组合意义。
「序列单调不增」，可以转化成只能向下或者向右走的路径。

具体来说，

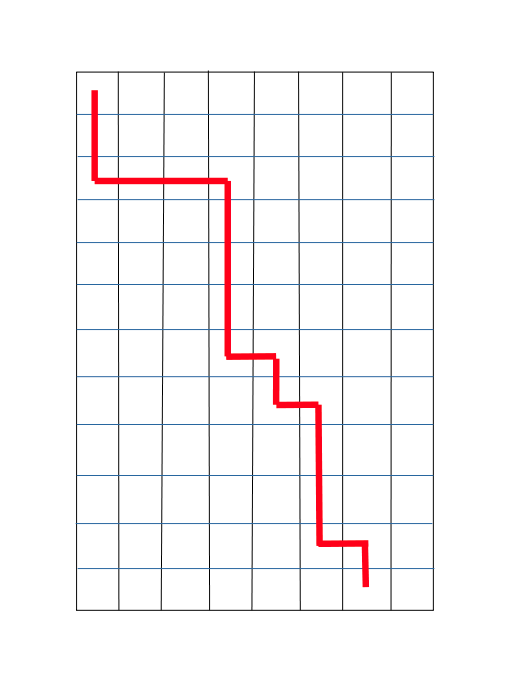
然后每一列的最低点就代表着这个位置选的数是几。

不难发现，一种路线与一种选数方式一一对应，比如说如图代表的数列就是10 10 10 6 5 2 1。

众所周知，这样的路线就有 \(\binom{n+m-1}{n-1}\) 种，
然后限制最后一位并没有什么用，直接限制掉路线的最低点就可以了。

还有ycx的想法，是下一个数会比上一个数少x，然后答案就是 \(x_1+x_2+……+x_{n-1}=m-k\) 的解的个数。
大概可以用隔板法可以推出相同的式子。

对了，最后套了个 \(lucas\) ，但没想到这玩意儿都会超纲。。。不过反正都会。。。

啊还有逆元只能线性求，不然会 \(T\) 的很惨。

总结：

小清新，但略水。全场暴切。

题目有多种转化方式，并不难想到。