射频电路中的电阻,电容,电感
电阻
电阻的作用
- 构成降压或者分压电路,用于器件的直流偏置
- 用作直流或射频电路的负载电阻完成某些特定的功能
电阻的分类
- 高密度碳介质合成电阻
- 镍或其他材料的线绕电阻
- 温度稳定材料的金属膜电阻
- 铝或铍基材料薄膜片电阻(射频微波使用较多)
电阻的性能
物质的电阻的大小与物质内部电子和空穴的迁移率有关。从外部看,物质的体电阻与电导率σ和物质的体积L×W×H有关,即
在射频电路中,电阻的等效电路比较复杂,不仅具有阻值,还会有引线电感和线间寄生电容,其性质将不再是纯电阻,而是“阻”与“抗”兼有,具体等效电路如图所示。
图中Ca表示电荷分离效应,也就是电阻引脚的极板间等效电容;Cb表示引线间电容;L为引线电感。
对于线绕电阻,其等效电路还要考虑线绕部分造成的电感量L1和绕线间的电容C1,引线间电容Cb与内部的绕线电容相比一般较小,可以忽略,等效电路如图所示。
以500Ω金属膜电阻为例(等效电路见上图),设两端的引线长度各为2.5cm,引线半径为0.2032mm,材料为铜,已知Ca为5pF,计算引线电感,并求出等效电路的总阻抗对频率的变化曲线,如下图所示。
从上图可以看出,在低频下阻抗即为电阻值,随着频率升高达到10MHz以上,电容Ca开始影响,导致总阻抗降低;当频率达到20GHz左右,出现并联谐振点;之后电感开始影响,阻抗加大。
电容
电容的性能
在低频下,电容器一般是平行板结构,其极板的几何尺寸远大于极板间距离,电容量定义为
式中,A是极板面积,d表示极板间距离,\(aε=ε_0ε_rb\)为极板为填充介质的介电常数。
理想状态下,电容极板间介质没有电流,在射频微波下,介质中存在电流,也就存在传导电流引起的损耗,更重要的是介质中的带电粒子具有一定的质量和惯性,在电磁场的作用下,很难随之同步振荡,在时间上有滞后现象,也会引起对能量的损耗
建立电容器的阻抗模型,由电导和电纳组成
式中,电流起因于电导
其中,\(aσ_db\)是介质的电导率
在射频/微波应用中,还要考虑引线电感L以及引线导体损耗的串联电阻Rs和介质损耗电阻Re,故电容器的等效电路如图所示。
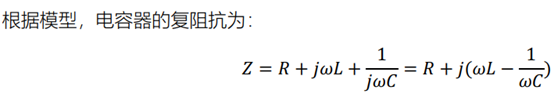
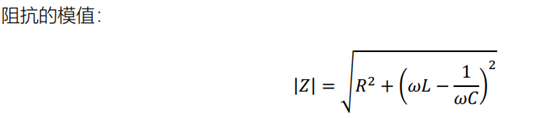
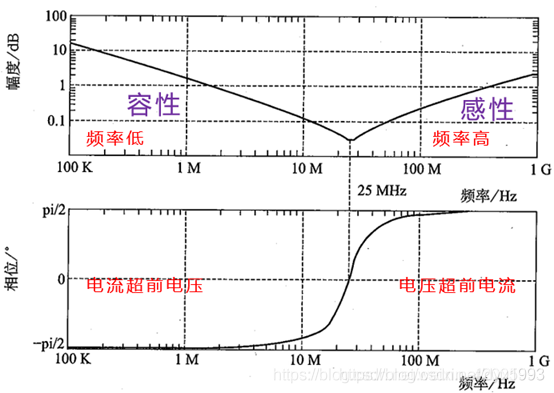
在频率较低时,感抗小于容抗,复阻抗的相位为负值,说明电流超前电压,电容充电。
在频率较高时,感抗大于容抗,复阻抗的相位为正值,说明电流滞后电压,呈现电感特性。
在谐振时,容抗和感抗相抵为0,此时电容的总阻抗最小,复阻抗相位为0,呈现纯电阻特性。
电容的频响曲线
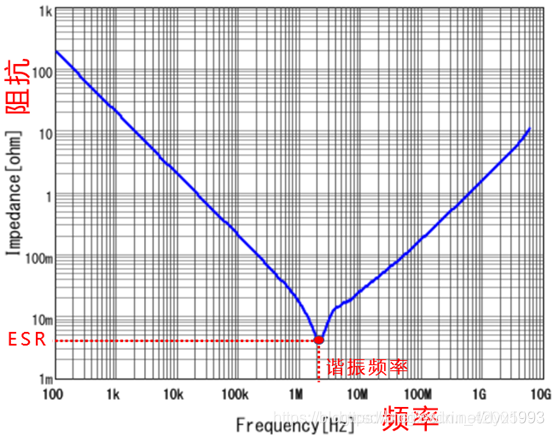
上图为电容的阻抗和频率曲线图。
在选择电容时,需要知道该电容的谐振频率,也可以算出其在各个频点上,电容的阻抗分别是多少。
滤波电容的选择
电容最大的作用就是滤波,选择电容就选阻值低的
在谐振频率点附近的阻抗比较低,所以,实际的去耦电容都有一定的工作范围,只有在谐振频率附近,电容才有很好的去耦作用。
这里看一下常规的MLCC陶瓷电容曲线图
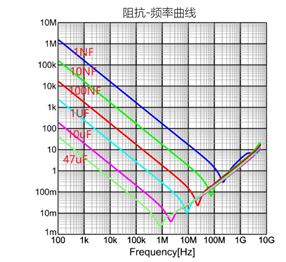
可以看出,不同电容的曲线不同,容量大的谐振频率低,ESR小,主要滤低频;容量小的,ESR大,谐振频率高,主要滤高频。
滤波电容的组合
实际电路中,我们想要宽带的去耦范围,可以用两种方法:第一种就是大电容和小电容并联,第二种就是相同电容并联。
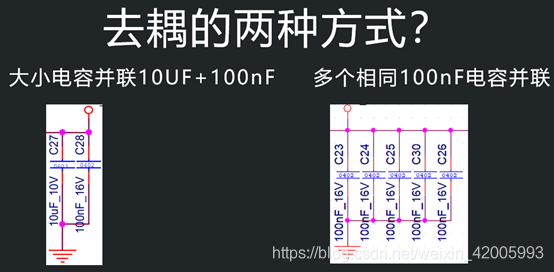
首先看第一种方法,大电容并联小电容。
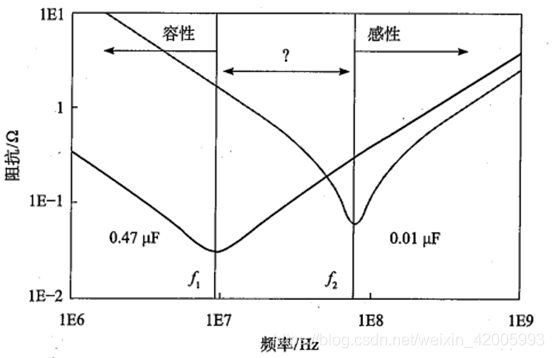
两个电容的谐振频率不一样,当频率比较低时,都呈现容性,在频率比较高的时候,都呈现感性。并联后两个电容的阻抗还是和原来一样,所以整体阻抗肯定小于任何一个单独的电容。
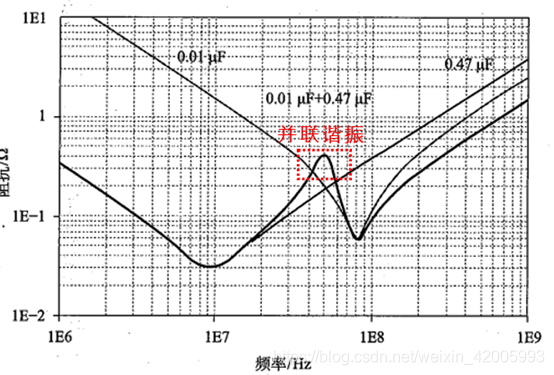
当频率大于f1,小于f2时,大电容呈现感性,小电容呈现容性,发生谐振点,构成LC并联谐振电路,并在某一个谐振点发生并联谐振,导致该点的阻抗很大。如果负载芯片的电流需求刚好落在这个频率,那么会导致该点的电压波动超标,所以,我们需要选好电容的搭配情况。
然后看第二种方法,n个电容并联的情况。
谐振频率和单个电容一样,但在谐振点的阻抗为原来的n分之一,因此,整体阻抗下降,曲线形状不变
参考文献
LC谐振电路 - 手抖哥 - 博客园 (cnblogs.com)
电感
电感的结构
在电子线路中常用的电感器一般是线圈结构,在高频率下也称为高频扼流圈。它的结构一般是用直导线沿柱状结构缠绕而成,如图所示。
电感的性能
导线的缠绕构成电感的主要部分,而导线本身的电感可以忽略不计,细长螺线管的电感量为
式中,r为螺线管半径,N为圈数,l为螺线管长度。
在考虑了寄生旁路电容Cs以及引线导体损耗的串联电阻Rs后,电感的等效电路图如图所示
例如,一个N=3.5的铜电感线圈,线圈半径为1.27mm,线圈长度为1.27mm,导线半径为63.5μm。假设它可以看做一细长螺线管,可求出其电感部分为L=61.4nH。其电容Cs可以看做平板电容产生的电容,极板间距离假设为两圈螺线间距离d=l/N=3.6×10-4mm,极板面积A=2alwire=2a(2πrN),lwire为绕成线圈的导线总长度,可求得Cs=0.087pF。导线的自身阻抗由式可求得,即0.034Ω。于是可得所示等效电路对应的阻抗频率特性曲线如图所示。
由上图中可以看出,这一铜电感线圈的高频特性已经完全不同于理想电感,在谐振点之前其阻抗升高很快,而在谐振点之后,由于寄生电容Cs的影响已经逐步处于优势地位而逐渐减小。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号