17.10.13

• 上午
  • 绝望地做BZOJ 1023
  • Ztraveler选讲，更绝望。
• 下午
  • BOZJ 1023 [SHOI2008]cactus仙人掌图

    真的是神题，想了我好久，做了我好久，改了我好久，调了我好久……

    （先吐槽一下：题目中的说的仙人图是什么？不是仙人掌图么。还有这个样例输入也是醉了）
       
    由于是仙人掌图（很特殊），所以如果把图中的环都缩点后，则形成一棵树。

    先看看在树上的话：
    一棵树中两点间的距离是唯一的，所以求出树的最长链就可以得出树的直径了。
    考虑dp，这个简单的树上求最长链应该会吧。
    显然一个以u为根的子树中的最长链为：以u为端点的最长和第二长链 相拼接。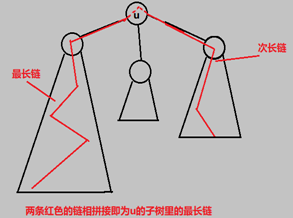
     
    令dp[u]表示在u所在的子树，以u为端点的最长链的长度，
    那么在树形dp到u节点时，
    枚举每个儿子，维护出已经枚举了的儿子所贡献的出的f[u]，
    那么对于当前枚举到的儿子所形成的最长链和f[u]相拼接，就可能会更新ans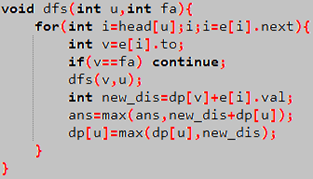
    

    （还是代码更直观）
       
    但是现在是仙人掌图诶，真的要Tarjan缩点使其成为一颗树么？
    还是算了吧。
    我想起曾经一次考试的有一道题，把仙人掌图不缩点却活生生的化成了一棵树，（当时是便于求lca）。
    做法是这样的（这么做好像不必要，因为网上的题解都没这样做，但当时我是这么想的）：
    dfs找出每一个环，把环中的边删去，然后把dfs找到的环的起点向环中其它的点连边：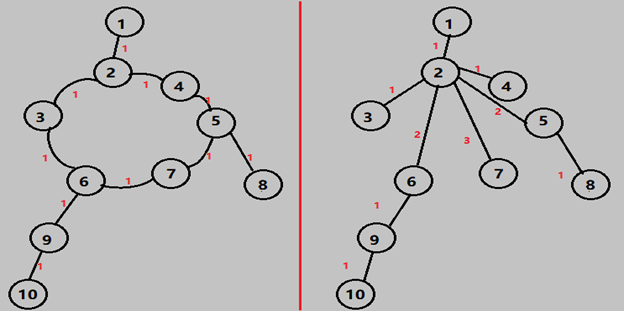
    
    （给删去的边打个del标记，以后若是遇到了就不枚举它。）
    （然后加一个belong[u]数组，表示u节点是属于第几个环，便于以后判断两个节点是否在同一个环）
    这样就形成了一棵树，可以向上面的那个dp那样跑了么？
       
    当然不行
    对于u节点的不在同一个环的两个儿子，这么做dp求ans没问题
    但在同一个环呢？这么求ans显然错了，
    因为环上两点的距离可不一定是两个点分别到该环起点的dis相加
    （当时卡了半天，还是去看了看别人的做法）
       
    我们的dp数组定义任然不变,对于dp数组的求法也任然不变,
    变的只是ans的求法：
    对于环上的那么多点，怎样求出最长的链呢。
    用单调队列。
    把同一环上的点存在一个数组中，并把存的东西翻倍，形成二倍序列。
    记环的长度为p，
    对于枚举到的点，用单调队列维护它后面p/2个点，
    使得（队首的节点的最长链+枚举到的点的最长链+队首的节点到枚举到的点在环上的最短距离）最小
    然后该值就可以去尝试更新ans了。
       
    然后就差不多了，只是感觉代码很恶心

    代码：

    #include<queue>
    #include<cstdio>
    #include<cstring>
    #include<iostream>
    using namespace std;
    struct edge{
    	int to,next;
    }e[300005];
    bool del[300005];
    int head[50005],fg[50005],from[50005],dp[50005];
    int belong[50005],tmp[50005],val[50005],who[50005];
    int ent=2,n,m,lim,ans,cnt;
    void add(int u,int v){
    	e[ent]=(edge){v,head[u]};
    	head[u]=ent++;
    }
    void dfs_get_tree(int u){
    	fg[u]=1;
    	for(int i=head[u];i;i=e[i].next) if(i<lim) {
    		int v=e[i].to;
    		if((i^from[u])==1) continue;
    		if(fg[v]==1){
    			++cnt;
    			int x=u; del[i]=1; del[i^1]=1;
    			do{
    				del[from[x]]=1;
    				del[from[x]^1]=1;
    				add(v,x); add(x,v);
    				belong[x]=cnt;
    				x=e[from[x]^1].to;
    			}while(x!=v);
    		}
    		if(fg[v]==0) from[v]=i,dfs_get_tree(v);
    	}
    	fg[u]=2;
    }
    void circle_queue(int be,int en,int u,int fa){
    	int p=0;
    	while(be!=en){
    		if(!del[be]&&e[be].to!=fa) tmp[++p]=e[be].to;
    		be=e[be].next;
    	}
    	tmp[++p]=u; int len=p/2,l=1,r=0;
    	if(p==1) return;
    	for(int i=1;i<=p;i++) tmp[p+i]=tmp[i];
    	int k=1;
    	for(int st=1;st<=p;st++){
    		while(k-st!=len){
    			++k;
    			while(r>=l&&val[r]<dp[tmp[k]]+k) r--;
    			val[++r]=dp[tmp[k]]+k,who[r]=k;
    			while(l<=r&&who[l]<=st) l++;
    		}
    		ans=max(ans,dp[tmp[st]]+dp[tmp[who[l]]]+who[l]-st);
    	}
    	for(int i=1;i<p;i++){
    		dp[u]=max(dp[u],dp[tmp[i]]+min(i,p-i));
    	}
    }
    void dp_get_ans(int u,int fa){
    	int last=head[u];
    	for(int i=head[u];i;i=e[i].next) if(!del[i]){
    		int v=e[i].to;
    		if(v==fa) continue;
    		dp_get_ans(v,u);
    		if(!belong[v]||belong[v]!=belong[e[last].to]){
    			circle_queue(last,i,u,fa);
    			last=i;
    		}
    	}
    	circle_queue(last,0,u,fa);
    }
    int main(){ 
    	scanf("%d%d",&n,&m);
    	for(int i=1,k,a,b;i<=m;i++){
    		scanf("%d%d",&k,&a);
    		for(int j=2;j<=k;j++)
    			scanf("%d",&b),add(a,b),add(b,a),a=b;
    	}
    	lim=ent;
    	dfs_get_tree(1);
    	dp_get_ans(1,0);
    	printf("%d",ans);
    	return 0;
    }

• 晚上
• BZOJ 1024 [SCOI2009]生日快乐

• n很小，直接dfs搜索
  dfs(x,y,d)表示x*y的蛋糕分为d分。
  为保证每个人分得的大小一样，在向下搜索时要按比例分割

  代码：

  #include<cstdio>
  #include<cstring>
  #include<iostream>
  using namespace std;
  double dfs(double x,double y,int k){
  	double ans=1e9;
  	if(k==1){
  		if(x<y) swap(x,y);
  		return x/y;
  	}
  	double mx=x/k,my=y/k;
  	for(int i=1;i<=k/2;i++){
  		ans=min(ans,max(dfs(mx*i,y,i),dfs(x-mx*i,y,k-i)));
  		ans=min(ans,max(dfs(x,my*i,i),dfs(x,y-my*i,k-i)));
  	}
  	return ans;
  }
  int main(){
  	double x,y; int k;
  	scanf("%lf%lf%d",&x,&y,&k);
  	printf("%.6lf",dfs(x,y,k));
  	return 0;
  }
  

• BZOJ 1025 [SCOI2009]游戏

• 1.问题转化：
  可以发现，对于一种n个位置之间的对应关系，就要生成n个排列（不算初始排列）
  那么有多种相互独立的对应关系时，生成的排列就是各个对应关系生成的排列数的最小公倍数
  比如：
  a b c d f
  a->b b->c c->a 为一种3个位置之间的对应关系，生成3个
  d->f f->d        为一种2个位置之间的对应关系，生成2个
  那么总的排列数为LCM（3,2）=6；
     
  接下来问题转化为求一些数的和为n时的LCM的种类
     
  2.dp解决：
  用质数去dp，因为质数之间的组合不会产生重复的LCM
     
  令dp[i][j]表示用前i种质数，那些数的和为n
  先是继承上一层的答案，
  即dp[i][j]=dp[i-1][j]
  然后枚举当前要用的数为prime[i]^k，
  即dp[i][j]+=dp[i-1][j-prime[i]^k]
     
  最后枚举第二维j，把dp值加起来，表示那些数加起来和为j时的LCM的种类。

  代码：

  #include<cstdio>
  #include<cstring>
  #include<iostream>
  #define ll long long
  using namespace std;
  bool np[1005];
  int prime[1005],cnt,n;
  ll dp[1005][1005],ans;
  void get_prime(){
  	for(int i=2;i<=1000;i++){
  		if(!np[i]) prime[++cnt]=i;
  		for(int j=1;j<=cnt&&prime[j]<=1000/i;j++){
  			np[prime[j]*i]=1;
  			if(i%prime[j]==0) break;
  		}
  	}
  } 
  int main(){
  	scanf("%d",&n);
  	get_prime();
  	dp[0][0]=1;
  	for(int i=1;i<=cnt;i++){
  		for(int j=0;j<=n;j++) dp[i][j]=dp[i-1][j];
  		for(int j=prime[i];j<=n;j*=prime[i])
  			for(int k=j;k<=n;k++)
  				dp[i][k]+=dp[i-1][k-j];
  	}
  	for(int j=0;j<=n;j++) ans+=dp[cnt][j];
  	printf("%lld",ans);
  	return 0;
  }

• BZOJ 1026 [SCOI2009]windy数

• 这是一个裸的数位DP！

  代码：

  #include<cstdio>
  #include<cstring>
  #include<iostream>
  #define ll long long
  using namespace std;
  int num[15],cnt;
  ll dp[15][15];
  ll a,b;
  int abs(int x){
  	return x>0?x:-x;
  }
  ll dfs(int p,int last,bool zero,bool up){
  	if(p==0) return !zero;
  	if(!up&&!zero&&dp[p][last]!=-1) return dp[p][last];
  	int r=9; ll ret=0;
  	if(up) r=num[p];
  	for(int i=0;i<=r;i++)if(abs(i-last)>=2||zero)
  		ret+=dfs(p-1,i,!i&&zero,i==r&&up);
  	if(!up&&!zero) return dp[p][last]=ret;
  	return ret;
  }
  ll work(ll x){
  	cnt=0;
  	memset(dp,-1,sizeof(dp));
  	while(x) num[++cnt]=x%10,x/=10;
  	return dfs(cnt,0,1,1);
  }
  int main(){
  	scanf("%lld%lld",&a,&b);
  	ll A=work(a-1);
  	ll B=work(b);
  	printf("%lld",B-A);
  	return 0;
  }

• BZOJ 1027 [JSOI2007]合金

很好的题
    
思路看网上大佬的题解吧、、、
http://blog.csdn.net/nlj1999/article/details/50545070
这个很好，很巧妙简洁地处理了共线/重点的问题。

代码：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#define INF 0x3f3f3f3f
#define eps (1e-9)
using namespace std;
struct par{
	double x,y;
	par operator -(const par &rtm) const{  //得向量 
		return (par){x-rtm.x,y-rtm.y};
	}
	double operator ^(const par &rtm) const{//叉乘 
		return x*rtm.y-y*rtm.x;
	}
	double operator *(const par &rtm) const{//点乘 
		return x*rtm.x+y*rtm.y;
	}
}A[505],B[505];
int dis[505][505],ans=INF;
int n,m;
int main(){
	scanf("%d%d",&n,&m); double x;
	for(int i=1;i<=n;i++) 
		scanf("%lf%lf%lf",&A[i].x,&A[i].y,&x);
	for(int i=1;i<=m;i++) 
		scanf("%lf%lf%lf",&B[i].x,&B[i].y,&x);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			dis[i][j]=INF;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){//枚举i->j的有向线段 
			bool fg=1;
			for(int k=1;k<=m;k++){
				double p=(B[k]-A[i])^(B[k]-A[j]);
				if(p>eps||(fabs(p)<eps&&(B[k]-A[i])*(B[k]-A[j])>eps)){
					fg=0;//与线段叉乘后不在"eps"那边 或 与线段共线但不在线段里面
					break;
				}
			}
			if(fg) dis[i][j]=1;
		}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
	for(int i=1;i<=n;i++) ans=min(ans,dis[i][i]);
	if(ans==INF) printf("-1");
	else printf("%d",ans);
	return 0;
}